EDO

An equal division of the octave (EDO or edo) is a tuning obtained by dividing the octave in a certain number of equal steps. This means that the interval between any two consecutive pitches is identical.

A tuning with n equal divisions of the octave is usually called "n-edo" ("n-EDO"). For instance, the predominant tuning system in the world today is 12edo (12-EDO).

An equal (pitch) division of the octave is the most common type of equal (pitch) division, which is a kind of equal-step tuning. Therefore, it is also a kind of arithmetic and harmonotonic tuning.

History

Tuning theorists first used the term "equal temperament" for edos designed to approximate low-complexity just intervals. The same term is still used today for all rank-1 temperaments. For example, 15edo can be referred to as 15-tone equal temperament (15-TET, 15-tET, 15tet, etc.), or more simply 15 equal temperament (15-ET, 15et, etc.).

The acronym "EDO" (EE-dee-oh) was coined by Daniel Anthony Stearns in 1999, originally standing for "equidistant divisions of the octave". More recently, the anacronym "edo" (EE-doh), spelled in lowercase, has also become common.

With the development of equal divisions of non-octave intervals (edonoi), some people started writing "ed2" ("ED2"), especially when naming a specific tuning.

Several alternate notations have been devised, including "edd" ("EDD"; equal division of the ditave), "DIV," and "EQ".⁠ ⁠^{[citation needed ]}

Formula

To find the step size of n-edo in terms of cents, divide 1200 by n. The size s of k steps of n-edo (k\n) is

[math]\displaystyle s = 1200 \cdot k/n[/math]

To find the step size of n-edo in terms of frequency ratio, take the n-th root of 2. For example, the step of 12edo is 2^1/12 (≈ 1.059). So the ratio c of the k steps of n-edo is

[math]\displaystyle c = 2^{k/n}[/math]

In particular, when k is 0, c is simply 1, because any number to the 0th power is 1. And when k = n, c is simply 2, because any number to the 1st power is itself.

EDO FAQ

What are EDO scales like?

Very straightforward to work with, the step size being so even and all. Some find the monotony bland, others find it a safe stable footing for musicmaking. The only property shared by all of them is the equality of their step-sizes; otherwise, their individual properties are as different as can be. The lower-numbered EDOs, especially 5 to 24, possess very strong and unique "characters", which some composers have found to be inspiring in their own right.

Why would I want to use an EDO?

If you are a guitarist (or a player of some other fretted string instrument, like a bass guitar, Appalachian dulcimer, ukulele, banjo, mandolin, sitar, saz, pipa, or zhong ruan), an EDO will provide you with the simplest possible fretboard layout, as all of the frets will go straight across the fretboard, regardless of how you want to tune the open strings. Speaking of string instruments fretted for EDOs, since ascending through the EDOs will crowd a fretboard relatively quickly, especially as one approaches the 30-something EDOs, equal divisions of the double octave (or higher multiple of the octave) are a relatively tidy compromise solution to the problem of laying out high-EDO fretboards.

More generally, EDOs allow for modulation to every single key in the tuning, without any alteration in harmonic properties, thus making transposition totally seamless. This also makes them somewhat easier to learn, as you do not have to memorize the harmonic and melodic variations that appear in various keys (which you would have to learn in JI, an unequal regular temperament, or a well-temperament, especially with smaller numbers of tones). For those accustomed to the "equality" of 12-TET, the equality of the alternative EDOs can be reassuringly familiar.

How do I explore so many?

It depends entirely on your desires as a musician!

If you are interested in exploring the unique merits and challenges of each EDO, irrespective of any desire to approximate Just intonation (or any other a priori musical goal), starting at the bottom and working your way up can be a most illuminating exercise.

If you're a classically-trained musician and you'd like to start with some EDOs that have some relationship to common-practice tonal music, starting with reasonably-low EDOs that give a good approximation to 3/2 (the perfect 5th) can be rewarding. These include 12, 17, 19, 22, 26, 27, 29, 31, 39, 41, 43, 45, 46, 49, 50, and 53. All of these can be notated with some variant on the A-G "circle of fifths" notation, while other EDOs, including 24, 34, 36, 38, 44, 48, or 51 involve more than one such circle.

Some EDOs, such as 26, 27, 32, 33, or 37 have fifths which are reasonably good but quite audibly not just. Other EDOs, such as 11, 13, 14, 15, 16, 18, 20, 21, 23, or 25, are of interest to the avid seeker of totally unusual sounds that have next-to-no connection with the common practice.

If your interest lies in the nuanced approximation of just intonation through EDOs, then delving into EDOs characterized by a strong local zeta peak could be especially captivating. Such EDOs, including 12, 19, 22, 27, 31, 34, 41, 46, 53, 58, 60, 65, 68, 72, 77, 80, 84, 87, 94, and 99, offer rich avenues for exploration in the quest for harmonic purity and transparent temperaments.

EDOs with a less pronounced, yet still noteworthy local zeta peak—specifically 10, 14, 15, 16, 17, 21, 24, 26, 29, 32, 36, 37, 38, 39, 43, 45, 48, 49, 50, 56, 62, 63, 82, 89, and 96 EDOs— present a unique palette for harmony explorers. Although these systems may lack the harmonic precision found in EDOs with more prominent zeta peaks, they strike an intriguing balance between consonance and more distant harmonic textures.

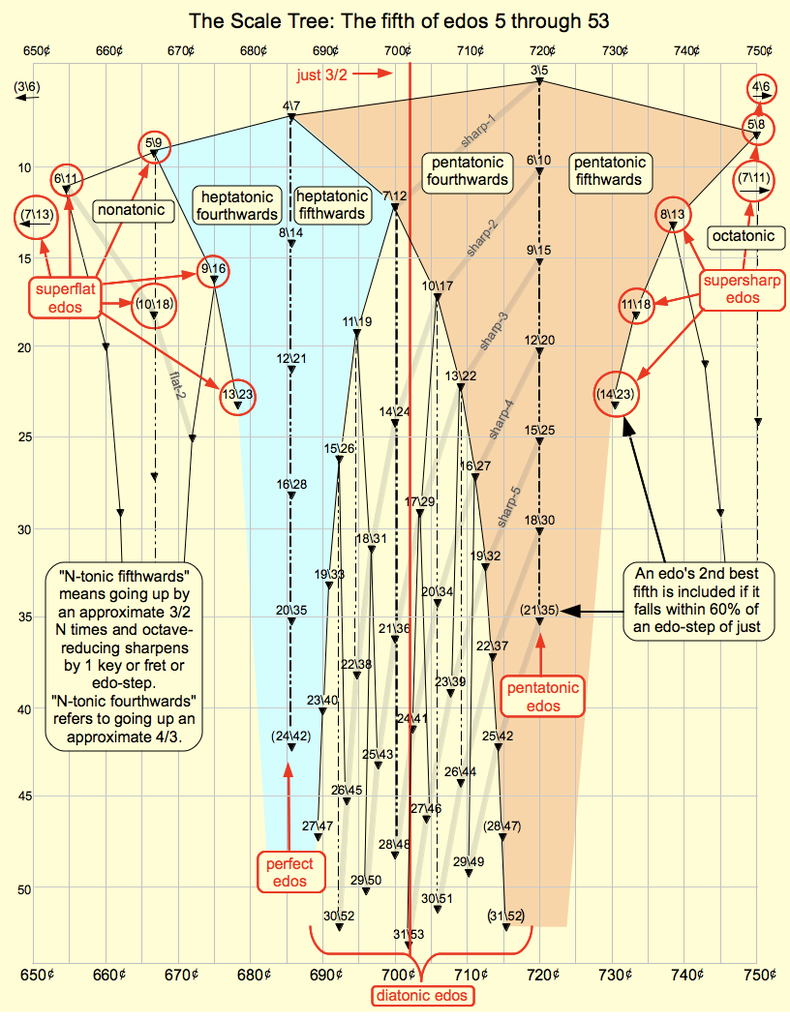
EDOs can be further subdivided and classified according to the size of the fifth, such as with Margo Schulter's gentle region or the distinction between negative, positive, doubly negative and doubly positive of R. H. M. Bosanquet. Kite Giedraitis has proposed these six categories, based on the size of the fifth. From narrowest to widest:

• superflat EDOs (9, 11, 13b, 16, 18b & 23) have a fifth narrower than four-sevenths of an octave = 4\7 = 686¢
• perfect EDOs (7, 14, 21, 28 & 35) have a fifth of 4\7 = 686¢
• diatonic EDOs (12, 17, 19, 22, 24, etc.) have a fifth between 686¢ and 720¢
• pentatonic EDOs (5, 10, 15, 20, 25 & 30) have a fifth of three-fifths of an octave = 3\5 = 720¢
• supersharp EDOs (8, 13 & 18) have a fifth wider than 3\5 = 720¢
• trivial EDOs (1, 2, 3, 4 and 6) have a fifth about 100¢ from just, and are contained in 12edo

Non-tuning properties

You will quickly find that the factorization of the total number of notes in each EDO has consequences for its structure and the way it relates to other EDOs. For example, 6 = 2 x 3, so 6edo contains all of the intervals in both 2edo and 3edo. On the other hand, 7 is a prime number, so no 7edo intervals are redundant with those of smaller EDOs. See Prime EDO and Highly composite EDO for more details.

The MOS paradigm is a fascinating way of thinking about building sub-scales of EDOs and relating them to non-EDO scales, as well as finding common melodic patterns between multiple EDOs.

Adding EDOs

Interesting phenomena may be observed when adding the cardinality of one equal division to that of another (octave or not). This really amounts to the consideration of adding the associated vals, which are the mappings to primes larger than 2. An EDO is defined by a certain number of steps equating to 2; if we have more steps equating to 3, we get a 3-limit val, and so forth. So, for example, 12edo can be written ⟨12], saying that twelve steps maps to 2, but the 3-limit val for 12 is ⟨12 19], telling us that 19 steps maps to 3, and the 5-limit val is ⟨12 19 28], telling us that 28 steps maps to 5.

If we add 12 and 19 we get another good division, 12 + 19 = 31. We can understand why this works if we look at it as adding vals; ⟨12 19 28] + ⟨19 30 44] = ⟨31 49 72]. The relative error in terms of relative cents is additive, and so sharpness and flatness cancel out, as they do for example with the approximation to 5 when adding 12 and 19. In terms of relative cents, the error of 12edo for the primes 3 and 5 is [-1.955 13.686] (the same as absolute cents) and the error of 19edo is [-11.429 -11.663], and this sums to [-13.384 2.023]. In relative cents the error of the fifth for 31edo is not much increased from 19edo, and on converting to absolute cents we find it is even better, and the error of the major third is much smaller due to the cancellation. When the errors are very sharp in one direction and very flat in another, as for instance with 15edo and 16edo, the sum (again 31edo) can have a much smaller error due to the cancellation. 24edo's flat fifth and 29edo's sharp fifth can be added to form 53edo.

We may also look at addition of EDOs in terms of MOS; if a\n is a generator for an n-edo MOS, and b\m for an m-edo MOS, where both of these are generators for the same linear temperament, then the mediant, (a + b)\(n + m), will be a generator for a MOS for the same temperament, this time in (n + m)-edo. A visual way of putting this is that through this addition of n and m, one becomes the accidentals or black keys, and the other the naturals or white keys. The choice of accidental/natural or black keys/white keys is a question of emphasis on the part of the composer or designer. Furthermore, one may add more than two numbers, hierarchically expanding the possibilities to double flats and sharps and beyond. This can be useful in designing keyboards and systems of notation.

Size of an EDO

When an edo divides the octave into fewer than 12 divisions (so that each step exceeds 100 cents), you might call it a macrotonal EDO. Of these, 1, 2, 3, 4 and 6 divide 12 and so are already available to anyone wishing to explore them. 5, 7 and 9 have arguably been used in various kinds of musical traditions in different parts of the world. The 13 EDOs of Xmas by Scott Thompson is a humorous demonstration of EDOs 1–13.

On the other hand, if you use the edo to tune a scale or regular temperament, the size of the edo does not matter so much (at least conceptually), as you don't need to use all of it. Some of the EDOs which can be used to tune various temperaments are listed on the optimal patent val page. Tuning a scale in just intonation by one of these EDOs can be regarded as automatically tempering it to the corresponding regular temperament.

To practically tune large edos through software tuning, one may take advantage of MIDI channels. See Tuning per channel.

All of these tools are also applicable to equal divisions of other (nonoctave) intervals as well.

What's the difference between EDOs and Equal Temperaments?

See EDO vs ET.

Individual pages for EDOs

0…999

0…99

0	1	2	3	4	5	6	7	8	9
10	11	12	13	14	15	16	17	18	19
20	21	22	23	24	25	26	27	28	29
30	31	32	33	34	35	36	37	38	39
40	41	42	43	44	45	46	47	48	49
50	51	52	53	54	55	56	57	58	59
60	61	62	63	64	65	66	67	68	69
70	71	72	73	74	75	76	77	78	79
80	81	82	83	84	85	86	87	88	89
90	91	92	93	94	95	96	97	98	99

1000…1999

1000, 1001, 1012, 1015, 1019, 1051, 1053, 1059, 1063, 1065, 1080, 1084, 1092, 1106, 1125, 1131, 1147, 1152, 1166, 1171, 1178, 1193, 1200, 1210, 1224, 1225, 1230, 1236, 1240, 1244, 1260, 1272, 1277, 1289, 1308, 1323, 1330, 1337, 1342, 1395, 1407, 1419, 1429, 1440, 1448, 1506, 1517, 1520, 1525, 1536, 1547, 1553, 1554, 1559, 1578, 1583, 1590, 1600, 1612, 1619, 1637, 1641, 1643, 1650, 1665, 1666, 1672, 1700, 1759, 1776, 1778, 1783, 1789, 1793, 1794, 1802, 1803, 1817, 1848, 1861, 1880, 1889, 1911, 1920, 1944, 1955, 1957, 1984, 1995

2000…9999

2000, 2016, 2019, 2022, 2023, 2024, 2029, 2048, 2072, 2100, 2113, 2118, 2129, 2153, 2190, 2200, 2320, 2444, 2460, 2477, 2513, 2520, 2544, 2554, 2619, 2660, 2684, 2711, 2730, 2777, 2809, 2814, 2897, 2901, 2912, 2960, 2964, 3072, 3079, 3084, 3085, 3125, 3178, 3325, 3395, 3422, 3476, 3498, 3558, 3566, 3578, 3600, 3684, 3696, 3776, 3920, 3990, 3991, 4004, 4096, 4172, 4190, 4231, 4296, 4320, 4327, 4349, 4380, 4419, 4501, 4650, 4655, 4973, 5040, 5280, 5320, 5544, 5585, 5902, 5941, 5985, 6079, 6380, 6650, 6664, 6691, 7033, 7315, 7980, 8103, 8192, 8193, 8194, 8269, 8539, 8736, 8745

10000 and up

10009, 10600, 11664, 12000, 12276, 12348, 12500, 13382, 14124, 14348, 14618, 14842, 15601, 15900, 16384, 16625, 16808, 17461, 18355, 20203, 20567, 21489, 25281, 28000, 30103, 30631, 31867, 31920, 32768, 34691, 46032, 50562, 58973, 65536, 73709, 78005, 79335, 80000, 86400, 98304, 99693, 102557, 103169, 111202, 120000, 148418, 190537, 196608, 241200, 253389, 258008, 324296, 571611, 762148, 1200000, 1714833, 1905370, 2547047, 2667518, 2901533, 4191814, 6000000, 11358058, 402653184, 5407372813

The largest physically possible EDO in a frequency range can be found through molecular physics such as the mean free path combined with the speed of sound in a given substance.

Non-integer EDO

A non-integer EDO can be defined as using a non-integer divisor to divide the octave. Typically, non-integer EDOs are understood as not containing the exact octave, so that they remain equal tunings. If the exact octave is retained and if the generator resets itself at each period, then this results in a MOS scale with only 1 small step.

All fractional EDOs are integer equal divisions of another integer interval. For example, (25/2)edo is equivalent to 25ed4. In general:

[math]\displaystyle (p/q) \text{edo} = p \text{-ed} 2^q[/math]

for integers p and q. Many irrational EDOs cannot be converted to integer equal divisions of another integer interval, so they are things of their own.

Non-integer EDOs can be written in decimal form, such as 12.1edo. This is often meant to be approximate, used in the context of octave stretch of an integer EDO, rather than as a fractional EDO.

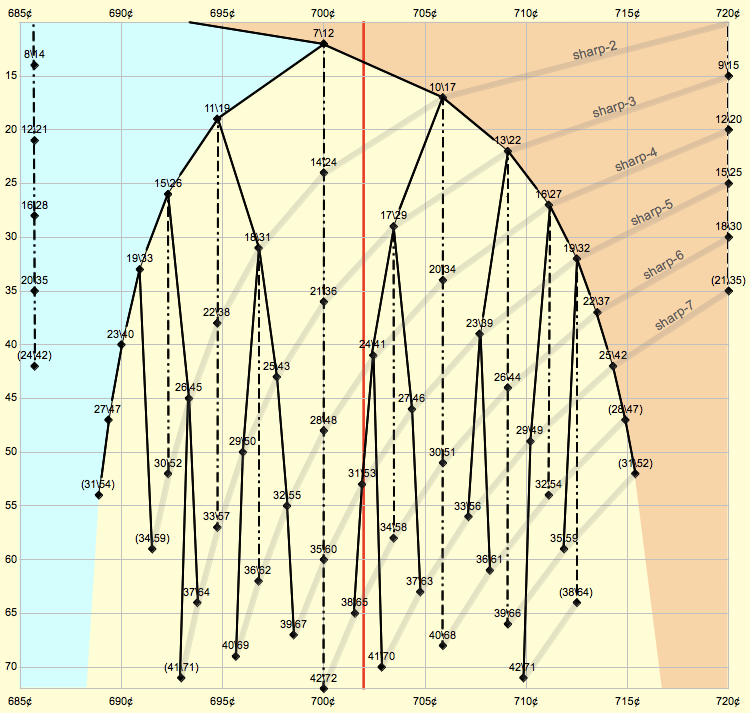
Scale tree

The scale tree, or Stern-Brocot tree, provides a visual map of the world of EDOs, based on fifth size.

The regular EDOs, up to 72edo:

Pergens

See also: Pergen § Pergens and EDOs

Pergens provide a JI-agnostic way to name the rank-2 scales of an EDO. This table lists every possible period/generator combination for EDOs 5-24, and for each coprime combination, the simplest pergen that it can represent. Non-coprime combinations such as P = 6\12, G = 4\12 are marked as "-".

EDO	Period	Generator in EDO steps
	in EDO steps	1	2	3	4	5	6	7	8	9	10	11
5	5 = P8	P4/2	P5
6	6 = P8	P4/2	-
	3 = P8/2	P5
7	7 = P8	P4/3	P5/2	P5
8	8 = P8	P4/3	-	P5
	4 = P8/2	P5	-
9	9 = P8	P4/4	P4/2	-	P5
	3 = P8/3	P5
10	10 = P8	P4/4	-	P5/2	-
	5 = P8/2	P5	P4/2
11	11 = P8	P4/5	P5/3	P5/2	P11/4	P5
12	12 = P8	P4/5	-	-	-	P5
	6 = P8/2	P5	-	-
	4 = P8/3	P5	-
	3 = P8/4	P5
13b	13 = P8	P4/6	P4/3	P4/2	P12/5	P12/4	P5
14	14 = P8	P4/6	-	P4/2	-	P11/4	-
	7 = P8/2	P5	P4/3	P4/2
15	15 = P8	P4/6	P4/3	-	P12/6	-	-	P11/3
	5 = P8/3	P5	P4/2
	3 = P8/5	P4/3
16	16 = P8	P4/7	-	P5/3	-	P12/5	-	P5
	8 = P8/2	P5	-	P5/3	-
	4 = P8/4	P5	-
17	17 = P8	P4/7	P5/5	P11/8	P11/6	P5/2	P11/4	P5	P11/3
18b	18 = P8	P4/8	-	-	-	P5/2	-	P12/4	-
	9 = P8/2	P5	P4/4	-	P4/2
	6 = P8/3	P5/2	-	-
	3 = P8/6	P5
19	19 = P8	P4/8	P4/4	P11/9	P4/2	P12/6	P12/5	ccP5/7	P5	P11/3
20	20 = P8	P4/8	-	P5/4	-	-	-	P11/4	-	c3P5/8
	10 = P8/2	M2/4	-	P5/4	-	-
	5 = P8/4	P4/2	P5
	4 = P8/5	P5/4	-
21	21 = P8	P4/9	P5/6	-	P5/3	P11/6	-	-	c3P4/9	-	P11/3
	7 = P8/3	P5/2	P5	P4/3
	3 = P8/7	P5/3
22	22 = P8	P4/9	-	P4/3	-	P12/7	-	P12/5	-	P5	-
	11 = P8/2	M2/4	P5	P4/3	P12/5	P12/7
23	23 = P8	P4/10	P4/5	P11/11	P12/9	P4/2	P12/6	ccP4/8	ccP4/7	P12/4	P5	P11/3
24	24 = P8	P4/10	-	-	-	P4/2	-	P5/2	-	-	-	c4P5/10
	12 = P8/2	M2/4	-	-	-	P4/2
	8 = P8/3	P5/2	-	P4/2
	6 = P8/4	P4/2	-	-
	4 = P8/6	P4/2	-
	3 = P8/8	P5
		1	2	3	4	5	6	7	8	9	10	11

Links and articles

• Alternative Names for EDOs
• Chuckles McGee's EDO personalities
• Collection of EDO impressions
• Consistency limits of small EDOs
• Distinct EDO Scales
• Expression to EDO calculator
• List of rank one temperaments by step size
• Macrotonal EDO
• Minimal consistent EDOs
• Monotonicity levels of small EDOs
• Relative errors of small EDOs
• Absolute errors of small EDOs
• Teen Tunes by Ivor Darreg
• Category:Equal divisions of the octave