35edo
| ← 34edo | 35edo | 36edo → |
(semiconvergent)
35 equal divisions of the octave (abbreviated 35edo or 35ed2), also called 35-tone equal temperament (35tet) or 35 equal temperament (35et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 35 equal parts of about 34.3 ¢ each. Each step represents a frequency ratio of 21/35, or the 35th root of 2.
Theory
As 35 is 5 times 7, 35edo allows for mixing the two smallest xenharmonic macrotonal edos: 5edo and 7edo. A single degree of 35edo represents the difference between 7edo's narrow fifth of 685.71 ¢ and 5edo's wide fifth of 720 ¢. Because it includes 7edo, 35edo tunes the 29th harmonic with only 1 ¢ of error.
35edo can also represent the 2.3.5.7.11.17 subgroup and 2.9.5.7.11.17 subgroup, because of the accuracy of 9 and the flatness of all other subgroup generators (7/5 and 17/11 stand out, having less than 1 cent error). Therefore among whitewood tunings it is very versatile; you can switch between these different subgroups if you don't mind having to use two different 3/2s to reach the inconsistent 9 (a characteristic of whitewood tunings), and if you ignore 22edo's more in-tune versions of 35edo MOS's and consistent representation of both subgroups.
35edo has the optimal patent val for greenwood and secund temperaments, as well as 11-limit muggles, and the 35f val is an excellent tuning for 13-limit muggles. 35edo is the largest edo with a lack of a diatonic scale (unless 7edo is considered a diatonic scale).
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -16.2 | -9.2 | -8.8 | +1.8 | -2.7 | +16.6 | +8.9 | -2.1 | +11.1 | +9.2 | -11.1 |
| Relative (%) | -47.4 | -26.7 | -25.7 | +5.3 | -8.0 | +48.5 | +25.9 | -6.1 | +32.3 | +26.9 | -32.5 | |
| Steps (reduced) |
55 (20) |
81 (11) |
98 (28) |
111 (6) |
121 (16) |
130 (25) |
137 (32) |
143 (3) |
149 (9) |
154 (14) |
158 (18) | |
Notation
The 7edo fifth is preferred as the diatonic generator for ups and downs notation due to being much easier to notate than the 5edo fifth (which involves E and F being enharmonic), as well as being closer to 3/2.
| Degrees | Cents | Ups and downs notation | Dual-fifth notation
based on closest 12edo interval | ||
|---|---|---|---|---|---|
| 0 | 0.000 | unison | 1 | D | 1sn, prime |
| 1 | 34.286 | up unison | ^1 | ^D | augmented 1sn |
| 2 | 68.571 | dup unison | ^^1 | ^^D | diminished 2nd |
| 3 | 102.857 | dud 2nd | vv2 | vvE | minor 2nd |
| 4 | 137.143 | down 2nd | v2 | vE | neutral 2nd |
| 5 | 171.429 | 2nd | 2 | E | submajor 2nd |
| 6 | 205.714 | up 2nd | ^2 | ^E | major 2nd |
| 7 | 240 | dup 2nd | ^^2 | ^^E | supermajor 2nd |
| 8 | 274.286 | dud 3rd | vv3 | vvF | diminished 3rd |
| 9 | 308.571 | down 3rd | v3 | vF | minor 3rd |
| 10 | 342.857 | 3rd | 3 | F | neutral 3rd |
| 11 | 377.143 | up 3rd | ^3 | ^F | major 3rd |
| 12 | 411.429 | dup 3rd | ^^3 | ^^F | augmented 3rd |
| 13 | 445.714 | dud 4th | vv4 | vvG | diminished 4th |
| 14 | 480 | down 4th | v4 | vG | minor 4th |
| 15 | 514.286 | 4th | 4 | G | major 4th |
| 16 | 548.571 | up 4th | ^4 | ^G | augmented 4th |
| 17 | 582.857 | dup 4th | ^^4 | ^^G | minor tritone |
| 18 | 617.143 | dud 5th | vv5 | vvA | major tritone |
| 19 | 651.429 | down 5th | v5 | vA | diminished 5th |
| 20 | 685.714 | 5th | 5 | A | minor 5th |
| 21 | 720 | up 5th | ^5 | ^A | major 5th |
| 22 | 754.286 | dup 5th | ^^5 | ^^A | augmented 5th |
| 23 | 788.571 | dud 6th | vv6 | vvB | diminished 6th |
| 24 | 822.857 | down 6th | v6 | vB | minor 6th |
| 25 | 857.143 | 6th | 6 | B | neutral 6th |
| 26 | 891.429 | up 6th | ^6 | ^B | major 6th |
| 27 | 925.714 | dup 6th | ^^6 | ^^B | augmented 6th |
| 28 | 960 | dud 7th | vv7 | vvC | diminished 7th |
| 29 | 994.286 | down 7th | v7 | vC | minor 7th |
| 30 | 1028.571 | 7th | 7 | C | superminor 7th |
| 31 | 1062.857 | up 7th | ^7 | ^C | neutral 7th |
| 32 | 1097.143 | dup 7th | ^^7 | ^^C | major 7th |
| 33 | 1131.429 | dud 8ve | vv8 | vvD | augmented 7th |
| 34 | 1165.714 | down 8ve | v8 | vD | diminished 8ve |
| 35 | 1200 | 8ve | 8 | D | 8ve |
Sagittal notation
Best fifth notation
This notation uses the same sagittal sequence as EDOs 30b and 40, and is a superset of the notation for 7-EDO.
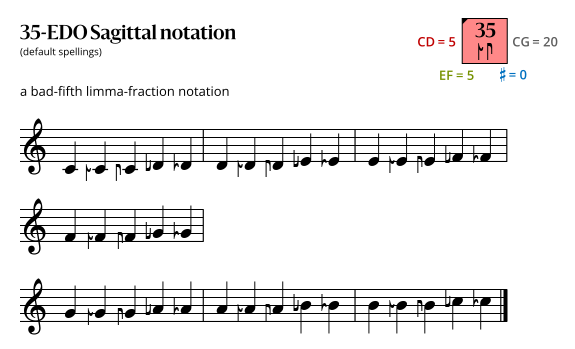
Second-best fifth notation
This notation uses the same sagittal sequence as 42-EDO, and is a superset of the notation for 5-EDO.

Chord Names
Ups and downs can be used to name 35edo chords. Because every interval is perfect, the quality can be omitted, and the words major, minor, augmented and diminished are never used. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are.
0-10-20 = C E G = C = C or C perfect
0-9-20 = C vE G = Cv = C down
0-11-20 = C ^E G = C^ = C up
0-10-19 = C E vG = C(v5) = C down-five
0-11-21 = C ^E ^G = C^(^5) = C up up-five
0-10-20-30 = C E G B = C7 = C seven
0-10-20-29 = C E G vB = C,v7 = C add down-seven
0-9-20-30 = C vE G B = Cv,7 = C down add-seven
0-9-20-29 = C vE G vB = Cv7 = C down seven
For a more complete list, see Ups and downs notation - Chords and Chord Progressions.
JI Intervals
(Bolded ratio indicates that the ratio is most accurately tuned by the given 35edo interval.)
| Degrees | Cents value | Ratios in 2.5.7.11.17 subgroup | Ratios with flat 3 | Ratios with sharp 3 | Ratios with best 9 |
| 0 | 0.000 | 1/1 | (see comma table) | ||
| 1 | 34.286 | 50/49, 121/119, 33/32 | 36/35 | 25/24 | 81/80 |
| 2 | 68.571 | 128/125 | 25/24 | 81/80 | |
| 3 | 102.857 | 17/16 | 15/14 | 16/15 | 18/17 |
| 4 | 137.143 | 12/11, 16/15 | |||
| 5 | 171.429 | 11/10 | 12/11 | 10/9 | |
| 6 | 205.714 | 9/8 | |||
| 7 | 240 | 8/7 | 7/6 | ||
| 8 | 274.286 | 20/17 | 7/6 | ||
| 9 | 308.571 | 6/5 | |||
| 10 | 342.857 | 17/14 | 6/5 | 11/9 | |
| 11 | 377.143 | 5/4 | |||
| 12 | 411.429 | 14/11 | |||
| 13 | 445.714 | 22/17, 32/25 | 9/7 | ||
| 14 | 480 | 4/3, 21/16 | |||
| 15 | 514.286 | 4/3 | |||
| 16 | 548.571 | 11/8 | |||
| 17 | 582.857 | 7/5 | 24/17 | 17/12 | |
| 18 | 617.143 | 10/7 | 17/12 | 24/17 | |
| 19 | 651.429 | 16/11 | |||
| 20 | 685.714 | 3/2 | |||
| 21 | 720 | 3/2, 32/21 | |||
| 22 | 754.286 | 17/11, 25/16 | 14/9 | ||
| 23 | 788.571 | 11/7 | |||
| 24 | 822.857 | 8/5 | |||
| 25 | 857.143 | 28/17 | 5/3 | 18/11 | |
| 26 | 891.429 | 5/3 | |||
| 27 | 925.714 | 17/10 | 12/7 | ||
| 28 | 960 | 7/4 | |||
| 29 | 994.286 | 16/9 | |||
| 30 | 1028.571 | 20/11 | 9/5 | ||
| 31 | 1062.857 | 11/6, 15/8 | |||
| 32 | 1097.143 | 32/17 | 28/15 | 15/8 | 17/9 |
| 33 | 1131.429 | ||||
| 34 | 1165.714 | ||||
| 3 | 1200 |
The following tables show how 15-odd-limit intervals are represented in 35edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 7/5, 10/7 | 0.345 | 1.0 |
| 13/12, 24/13 | 1.430 | 4.2 |
| 9/8, 16/9 | 1.804 | 5.3 |
| 11/8, 16/11 | 2.747 | 8.0 |
| 11/9, 18/11 | 4.551 | 13.3 |
| 11/7, 14/11 | 6.079 | 17.7 |
| 11/10, 20/11 | 6.424 | 18.7 |
| 5/3, 6/5 | 7.070 | 20.6 |
| 7/6, 12/7 | 7.415 | 21.6 |
| 15/13, 26/15 | 7.741 | 22.6 |
| 13/10, 20/13 | 8.500 | 24.8 |
| 7/4, 8/7 | 8.826 | 25.7 |
| 13/7, 14/13 | 8.845 | 25.8 |
| 15/8, 16/15 | 8.874 | 25.9 |
| 5/4, 8/5 | 9.171 | 26.7 |
| 9/7, 14/9 | 10.630 | 31.0 |
| 9/5, 10/9 | 10.975 | 32.0 |
| 15/11, 22/15 | 11.621 | 33.9 |
| 11/6, 12/11 | 13.494 | 39.4 |
| 13/9, 18/13 | 14.811 | 43.2 |
| 13/11, 22/13 | 14.924 | 43.5 |
| 3/2, 4/3 | 16.241 | 47.4 |
| 15/14, 28/15 | 16.586 | 48.4 |
| 13/8, 16/13 | 16.615 | 48.5 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 7/5, 10/7 | 0.345 | 1.0 |
| 11/8, 16/11 | 2.747 | 8.0 |
| 11/7, 14/11 | 6.079 | 17.7 |
| 11/10, 20/11 | 6.424 | 18.7 |
| 5/3, 6/5 | 7.070 | 20.6 |
| 7/6, 12/7 | 7.415 | 21.6 |
| 7/4, 8/7 | 8.826 | 25.7 |
| 5/4, 8/5 | 9.171 | 26.7 |
| 11/6, 12/11 | 13.494 | 39.4 |
| 3/2, 4/3 | 16.241 | 47.4 |
| 15/14, 28/15 | 16.586 | 48.4 |
| 13/8, 16/13 | 16.615 | 48.5 |
| 13/11, 22/13 | 19.362 | 56.5 |
| 15/11, 22/15 | 22.665 | 66.1 |
| 9/5, 10/9 | 23.311 | 68.0 |
| 9/7, 14/9 | 23.656 | 69.0 |
| 15/8, 16/15 | 25.412 | 74.1 |
| 13/7, 14/13 | 25.441 | 74.2 |
| 13/10, 20/13 | 25.786 | 75.2 |
| 11/9, 18/11 | 29.735 | 86.7 |
| 9/8, 16/9 | 32.481 | 94.7 |
| 13/12, 24/13 | 32.856 | 95.8 |
| 15/13, 26/15 | 42.027 | 122.6 |
| 13/9, 18/13 | 49.097 | 143.2 |
Regular temperament properties
Rank-2 temperaments
Commas
35et tempers out the following commas. (Note: This assumes the val ⟨35 55 81 98 121 130].)
| Prime limit |
Ratio[1] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 2187/2048 | [-11 7⟩ | 113.69 | Lawa | Whitewood comma, apotome, Pythagorean chroma |
| 5 | 6561/6250 | [-1 8 -5⟩ | 84.07 | Quingu | Ripple comma |
| 5 | (15 digits) | [9 9 -10⟩ | 54.46 | Quinbigu | Mynic comma |
| 5 | 3125/3072 | [-10 -1 5⟩ | 29.61 | Laquinyo | Magic comma, small diesis |
| 7 | 405/392 | [-3 4 1 -2⟩ | 56.48 | Ruruyo | Greenwoodma |
| 7 | 16807/16384 | [-14 0 0 5⟩ | 44.13 | Laquinzo | Cloudy comma |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.79 | Zotrigu | Septimal semicomma, starling comma |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.58 | Loruru | Mothwellsma |
| 13 | 66/65 | [1 1 -1 0 1 -1⟩ | 26.43 | Thulogu | Winmeanma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints
Scales
- A good place to start using 35-EDO is with the sub-diatonic scale, that is a MOS of 3L2s: 9 4 9 9 4.
- Also available is the amulet scale[idiosyncratic term], approximated from magic in 25edo: 3 1 3 3 1 3 4 3 3 1 3 4 3
- Approximations of gamelan scales:
- 5-tone pelog: 3 5 12 3 12
- 7-tone pelog: 3 5 7 5 3 8 4
- 5-tone slendro: 7 7 7 7 7
Instruments
Lumatone
35edo can be played on the Lumatone. See Lumatone mapping for 35edo
Skip fretting
Skip fretting system 35 3 8 is a skip fretting system for 35edo. All examples on this page are for 7-string guitar.
- Prime harmonics
1/1: string 2 open
2/1: string 3 fret 9 and string 6 fret 1
3/2: string 3 fret 4 and string 4 fret 13
5/4: string 3 fret 1, string 4 fret 10, and string 7 fret 2
7/4: string 4 fret 4
11/8: string 1 fret 8, string 4 open, and string 5 fret 9
13/8: string 1 fret 11, string 4 fret 3, and string 5 fret 12
17/16: string 2 fret 1 and string 3 fret 10
Music
- G2 Manifold (2020) – uses a combination of 5edo and 7edo, which can be classified as a 35edo subset.
- Penguins...? (2024)
- Self-Destructing Mechanical Forest (in Secund[9])
- Little Prelude & Fugue, "The Bijingle" (2014)
- MicroFugue on Happy Birthday for Baroque Ensemble (2023)
- DarkSciFiThing (2024)