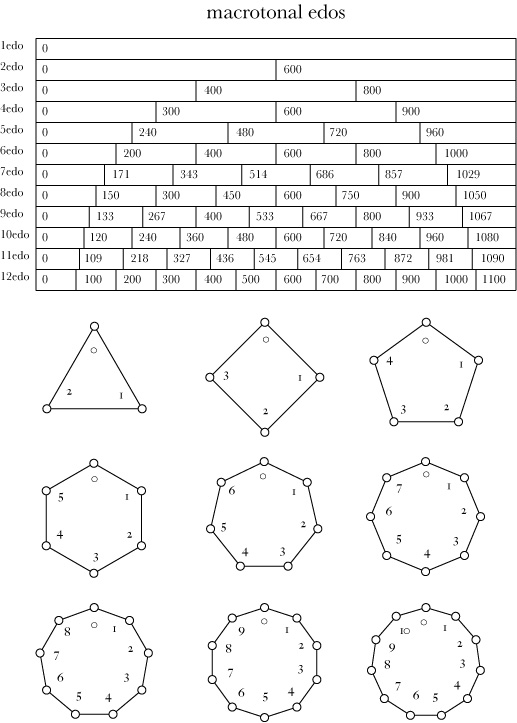
Macrotonal EDO

From Xenharmonic Wiki
(Redirected from Macrotonal edos)
Jump to navigation Jump to search

edo: "equal division of the octave". A tuning system which derives its pitches by dividing an octave into some number of logarithmically equal steps. Our cultural monotuning of 12edo is, of course, the most prevalent example of an edo, and often the only one a Western composer composes in.

Macrotonal: literally, "(noticeably) larger than a half step". A "macrotonal" scale would be one where all step sizes exceed 100 cents (in theory) or at least equal 103.5 cents (in practice). Paradoxically, "macrotonal" is a subset of "microtonal," according to the loose definition of microtonal meaning "tuning systems other than 12-tone equal temperament". Just as paradoxically, macrotones will become incisive steps relative to hyperoctaves larger than 1300 cents (13edt being the canonical example of this paradox), and also "emphatic" approaches to a scale degree (meantone temperament being the canonical example of this paradox).

"Macrotonal Edo," then, refers to a tuning system which cuts the octave into fewer than 12 equal parts.

  • 1edo is a sparse scale indeed, since it consists of one pitch and its octave transpositions.
  • 2, 3, and 4edo are all represented in 12edo (since 12 is divisible by 2, 3, and 4). In 12edo, they function as dyads and chords, not as scales (tritone, augmented triad, and fully diminished seventh chord, respectively).
  • 5edo is the first xenharmonic edo. Its third degree, at 720 cents (and its inversion at 480 cents) seems to represent an upper limit for how wide you can make a "fifth" and still call it a "fifth". The single step (240 cents) confounds an interval naming system based on 7-tone scales, and may sound like a second or third depending on timbre and context. Its fourth degree, at 960 cents, is 9 cents away from the seventh harmonic, 7:4, at 969 cents. Some Indonesian slendro scales come close to 5edo, as do some scales found in African tribal musics.
  • 6edo is equivalent to 12edo's "whole tone scale," and does sound distinctly different from 12edo treated in the traditional way.
  • 7edo distinguishes a second, a third, a fourth, a fifth, a sixth, and a seventh, and thus passes as a complete heptatonic scale. It only distinguishes one neutral version of each interval class (as opposed to the major and minor seconds, thirds, sixths and sevenths of some more complex systems). Its fourth degree, at 686 cents (and its inversion at 514 cents), seems to represent a lower limit for how narrow you can make a "fifth" and still call it a "fifth". 7edo contains a pentatonic moment-of-symmetry scale: 2L 3s (1 2 1 2 1) (the same MOS class as traditional chain-of-fifths pentatonics such as is possible in Pythagorean, meantone, 12edo, and some higher edos).
  • 8edo has no perfect fourths or fifths and sounds very xenharmonic. It is playable in 24edo as a subset. It contains one MOS scale: 3L 2s (2 1 2 1 2). It can be treated as two fully diminished seventh chords separated by a 150-cent neutral second.
  • 9edo contains a pentatonic MOS scale -- 2L 3s (1 3 1 3 1) -- with a heptatonic extension -- 2L 5s (1 1 2 1 1 2 1, sometimes called "mavila" or "antidiatonic"). Indonesian pelog scales sometimes use five-tone subsets of a seven-tone superset in a similar way. 9edo contains three augmented triads separated by a 133 cent neutral tone.
  • 10edo contains a very close approximation of the 13th harmonic, and an MOS scale 3L 4s (1 2 1 2 1 2 1). It can be treated as two 5edos separated by a 120 cent [large] semitone. 10edo is the only macrotonal edo which contains another xenharmonic macrotonal edo: it contains 5edo, in much the same way that 12edo contains 6edo, the "whole tone scale". It is arguably the only macrotonal edo that can be said to contain (unequal) tetrachords: its "perfect fourth," at four degrees, can be divided 1-1-2, 1-2-1, or 2-1-1.
  • 11edo is a xenharmonic tuning with a minor subfifth rather than a major fifth, and a decent approximation of the 11th harmonic and the septimal supermajor third (also: a sharp but passable harmonic seventh). Since 11 is a prime number, 11edo offers several MOS scales: 4L 3s (2 1 2 1 2 1 2), 3L 2s (3 1 3 1 3), 3L 5s (1 2 1 1 2 1 2 1), 2L 3s (1 3 1 3 1), 2L 5s (1 3 1 1 1 3 1) and others. It many ways, it is more complex than 12edo, even with one fewer tone. 11edo is a subset of that odd duck 22edo.

Macrotonal edos offer as one possible starting point for exploring non-12 tunings. Each offers its own set of unique constraints. Some seem to offer less variety than 12edo does (so are, in a way, simple -- eg. 5edo, 7edo), and some seem to offer more variety (eg. 11edo). As a set, they offer abundant variety and could keep a student happily confused for a good while, perhaps a lifetime.

If what you're after is very close approximations to low-number frequency ratios, you will find only one example here: 9edo has a very close approximation to 7/6 and 12/7. You will, however, find something else.

Note that "macrotonal edos" is a finite set containing 11 members. "Xenharmonic macrotonal edos" would exclude those which are subsets of 12edo (1-4 & 6), & would thus contain 6 members (5, 7, 8, 9, 10, 11).

EDO Families

Macrotonal edos (or any edo really) are available in larger edos which are multiples of them; the edos which are multiples of the same smaller edo can be thought of as being "related," perhaps even "in the same family" as one another. This becomes especially significant with linear temperaments such as Blackwood Temperament which use some division of the octave (in the case of Blackwood, a fifth of an octave) as the period. It also suggests a family of superscales that one could use to expand upon the potential of a simpler scale: for instance, 14edo as a superscale containing two 7edos. Here are some edo families:

macrotonal_edos.jpg

macrotonal_edos.pdf

Retrieved from "https://en.xen.wiki/index.php?title=Macrotonal_EDO&oldid=115398"