9edo

← 8edo

9edo

10edo →

Prime factorization	32
Step size	133.333 ¢
Fifth	5\9 (666.667 ¢)
Semitones (A1:m2)	-1:2 (-133.3 ¢ : 266.7 ¢)
Consistency limit	7
Distinct consistency limit	5

9 equal divisions of the octave (abbreviated 9edo or 9ed2), also called 9-tone equal temperament (9tet) or 9 equal temperament (9et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 9 equal parts of about 133 ¢ each. Each step represents a frequency ratio of 2^1/9, or the 9th root of 2.

Theory

A chromatic 9edo scale on C.

9edo is the most basic tuning which supports an antidiatonic scale. Its fifth is considerably flatter than just, but still falls into the category of "fifth" despite this. 9edo is also the first edo to have distinct major and minor chords (if 5edo's tendo and arto chords are ignored).

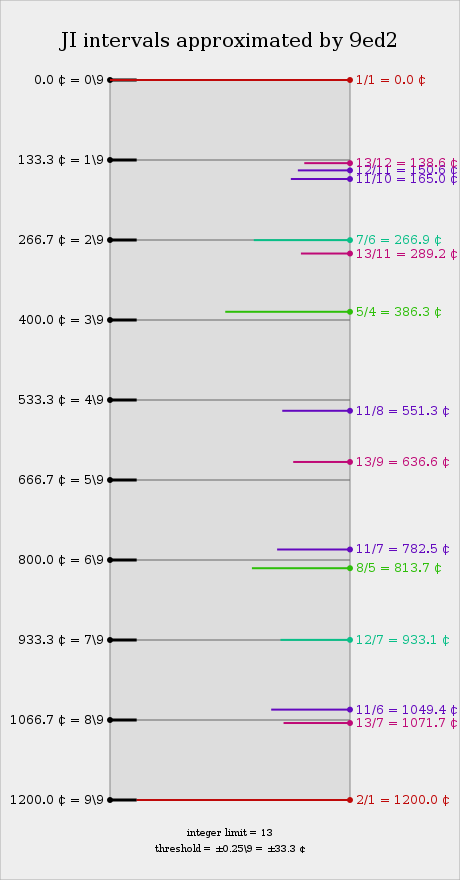
9edo splits the octave into three parts, each representing the major third 5/4, similarly to 12edo, which is of moderate accuracy. A similarly crude approximation of 11/8 (a sharp fourth) is available at the perfect fourth of 4 steps, which means 9edo can be seen as a simple 2.5.11 system. Looking at the intervals in this subgroup, the submajor second 11/10 is tuned to 133 cents (extremely flat) and 25/22 is even worse (but still consistent); the supermajor sixth 55/32 is tuned very accurately at 933 cents (only slightly flat). Overall, 9edo is not a great system for approximating low-complexity JI intervals consistently. However, if we turn to inconsistent representations, we see quite a few options before us. In particular, the 9edo scale has the peculiar property of representing certain 7-limit intervals almost exactly, but not the harmonic 7/4 (a subminor seventh) itself (unless semaphore, which equates it with the supermajor sixth 12/7, is taken as an acceptable temperament in this tuning). A 7-limit version of 9edo goes

1: 27/25 133.238 large limma, BP small semitone

2: 7/6 266.871 septimal minor third

3: 63/50 400.108 quasi-equal major third

4: 49/36 533.742 Arabic lute acute fourth

5: 72/49 666.258 Arabic lute grave fifth

6: 100/63 799.892 quasi-equal minor sixth

7: 12/7 933.129 septimal major sixth

8: 50/27 1066.762 grave major seventh

9: 2/1 1200.000 octave

Chords such as 1/1 – 7/6 – 49/36 – 12/7 are therefore natural ones for 9edo. The above scale generates the just intonation subgroup 2.27/25.7/3, which is closely related to 9edo.

Odd harmonics

Approximation of odd harmonics in 9edo

Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	-35.3	+13.7	-35.5	+62.8	-18.0	-40.5	-21.6	+28.4	-30.8	+62.6	+38.4
	Relative (%)	-26.5	+10.3	-26.6	+47.1	-13.5	-30.4	-16.2	+21.3	-23.1	+46.9	+28.8
Steps (reduced)		14 (5)	21 (3)	25 (7)	29 (2)	31 (4)	33 (6)	35 (8)	37 (1)	38 (2)	40 (4)	41 (5)

Subsets and supersets

9edo is the first odd composite edo, containing 3edo as a subset.

The ennealimmal temperament contains 9edo as a subset (splitting 2/1 into 9 equal parts) and is excellent in the 7-limit. However, 9edo by itself tempers out 27/25 by patent val, rather than representing it as 1\9 like in ennealimmal, although the 9bccd val contains both the 27/25 and 7/6 representations above and therefore supports ennealimmal.

Notation

This tuning can be notated with conventional notation, including the staff, note names, relative notation, etc. in two ways.

The first and most common defines sharp/flat, major/minor and aug/dim in terms of the native antidiatonic scale, such that sharp is higher pitched than flat, and major/aug is wider than minor/dim, as would be expected. Because it does not follow diatonic conventions, conventional interval arithmetic no longer works, e.g. M2 + M2 isn't M3, and D + M2 isn't E. Because antidiatonic is the sister scale to diatonic, you can solve this by swapping major and minor in interval arithmetic rules. Note that the notes that form chords are different from in diatonic: for example, a major chord, P1 – M3 – P5, is approximately 4:5:6 as would be expected, but is notated C-E#-G on C.

Alternatively, one can essentially pretend the native antidiatonic scale is a normal diatonic, meaning that sharp is lower in pitch than flat (since the "S" step is larger than the "L" step) and major/aug is narrower than minor/dim. The primary purpose of doing this is to allow music notated in 12edo or another diatonic system to be directly translated "on the fly" (or to allow support for this tuning in tools that only allow chain-of-fifths notation), and it carries over the way interval arithmetic works from diatonic notation, at the cost of notating the sizes of intervals and the shapes of chords incorrectly: that is, a major chord, P1-M3-P5, is notated C-E-G on C, but is no longer ~4:5:6 (since the third is closer to a minor third).

For the sake of clarity, the first notation is commonly called "melodic notation", and the second is called "harmonic notation", but this is a bit of a misnomer as both preserve different features of the notation of harmony.

Comparison of notations

	P1-M3-P5 ~ 4-5-6	P1-M3-P5 = C-E-G on C
Diatonic notation	No	Yes
Antidiatonic notation	Yes	No

In this notation, the enharmonic unison is the augmented 2nd, e.g. E♭ to F♯.

degree	cents	Approximate Ratios	Antidiatonic Major wider than minor		Diatonic Major narrower than minor		Audio
0	0.00	1/1	perfect unison	D	perfect unison	D
1	133.33	14/13 (+5.035), 13/12 (−5.239), 12/11 (−17.304)	minor 2nd	E	major 2nd	E
2	266.67	7/6 (−0.204)	major 2nd, minor 3rd	E♯, F♭	minor 2nd, major 3rd	E♭, F♯
3	400.00	5/4 (+13.686), 14/11 (−17.508), 9/7 (−35.084)	major 3rd	F	minor 3rd	F
4	533.33	4/3 (+35.288), 11/8 (−17.985)	perfect 4th	G	perfect 4th	G
5	666.67	16/11 (+17.985), 3/2 (−35.288)	perfect 5th	A	perfect 5th	A
6	800.00	14/9 (+35.084) 11/7 (+17.508), 8/5 (−13.686)	minor 6th	B	major 6th	B
7	933.33	12/7 (+0.204)	major 6th, minor 7th	B♯, C♭	minor 6th, major 7th	B♭, C♯
8	1066.67	11/6 (+17.304) 13/7 (−5.035)	major 7th	C	minor 7th	C
9	1200.00	2/1	octave	D	octave	D

Sagittal notation

This notation uses the same sagittal sequence as 14-EDO.

Approximation to JI

Selected just intervals

Zeta peak index

Tuning			Strength				Octave (cents)		Integer limit
ZPI	Steps per 8ve	Step size (cents)	Height		Integral	Gap	Size	Stretch	Consistent	Distinct
			Tempered	Pure
22zpi	8.949992	134.078333	3.998567	3.622488	0.954565	13.186387	1206.704993	6.704993	8	6

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
				Absolute (¢)	Relative (%)
2.3	[-14 9⟩	[⟨9 14]]	+11.13	11.24	8.35
2.3.5	27/25, 128/125	[⟨9 14 21]]	+5.36	12.18	9.10
2.3.5.7	21/20, 36/35, 49/48	[⟨9 14 21 25]]	+7.20	11.02	8.21
2.3.5.7.11	21/20, 33/32, 36/35, 45/44	[⟨9 14 21 25 31]]	+6.80	9.89	7.37

Uniform maps

13-limit uniform maps between 8.8 and 9.2

Min. size	Max. size	Wart notation	Map
8.7827	8.8165	9cee	⟨9 14 20 25 30 33]
8.8165	8.8289	9c	⟨9 14 20 25 31 33]
8.8289	9.0530	9	⟨9 14 21 25 31 33]
9.0530	9.0833	9f	⟨9 14 21 25 31 34]
9.0833	9.1055	9df	⟨9 14 21 26 31 34]
9.1055	9.1485	9def	⟨9 14 21 26 32 34]
9.1485	9.2595	9bdef	⟨9 15 21 26 32 34]

Commas

9et tempers out the following commas. This assumes val ⟨9 14 21 25 31 33].

Prime limit	Ratio	Monzo	Cents	Color name	Name
3	19683/16384	[-14 9⟩	317.59	Lawa 2nd	Pythagorean augmented second
5	27/25	[0 3 -2⟩	133.24	Gugu	Bug comma, large limma
5	135/128	[-7 3 1⟩	92.18	Layobi	Mavila comma, major chroma
5	16875/16384	[-14 3 4⟩	51.12	Laquadyo	Negri comma
5	128/125	[7 0 -3⟩	41.06	Trigu	Augmented comma, lesser diesis
5	(14 digits)	[-21 3 7⟩	10.06	Lasepyo	Semicomma
7	36/35	[2 2 -1 -1⟩	48.77	Rugu	Mint comma, septimal quarter tone
7	525/512	[-9 1 2 1⟩	43.41	Lazoyoyo	Avicennma
7	49/48	[-4 -1 0 2⟩	35.70	Zozo	Semaphoresma, slendro diesis
7	686/675	[1 -3 -2 3⟩	27.99	Trizo-agugu	Senga
7	2430/2401	[1 5 1 -4⟩	20.79	Quadru-ayo	Nuwell comma
7	1728/1715	[6 3 -1 -3⟩	13.07	Triru-agu	Orwellisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Marvel comma
7	6144/6125	[11 1 -3 -2⟩	5.36	Sarurutrigu	Porwell comma
7	65625/65536	[-16 1 5 1⟩	2.35	Lazoquinyo	Horwell comma
7	(16 digits)	[-11 -9 0 9⟩	1.84	Tritrizo	Septimal ennealimma
11	99/98	[-1 2 0 -2 1⟩	17.58	Loruru	Mothwellsma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	540/539	[2 3 1 -2 -1⟩	3.21	Lururuyo	Swetisma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap comma, biome comma
13	676/675	[2 -3 -2 0 0 2⟩	2.56	Bithogu	Island comma

Rank-2 temperaments

9edo contains a pentatonic mos scale produced by stacking 4/9 of 2L 3s (1 3 1 3 1), which has a heptatonic extension, 2L 5s (1 1 2 1 1 2 1, sometimes called "mavila" or "antidiatonic").

You can also use the 2/9, which generates mos scales of 1L 3s (3 2 2 2) and 4L 1s (2 2 2 2 1) and can be interpreted as either an extremely sharp bug scale or an extremely flat orwell one.

Historical (and other) relevance

Indonesian pelog scales sometimes use five-tone subsets of a seven-tone superset in a similar way as the 5-tone and 7-tone mavila scale (see Rank-2 temperaments), and it has been suggested that Indonesian gamelan music stems from a 9edo tradition.

As a division of the octave into 3² parts, i. e. a dominant position of the number 3, 9edo also has some suitability as base tuning for Klingon music (since the tradtional Klingon number system is also based on 3). See, for this:

Levi McClain, Klingon music theory is weird

Diagrams

Instruments

Ukulele (MicroUke 1.2) set to 9edo with 40 lb. test fishing line (by cenobyte)

Music

Main article: Music in 9edo

Ear training

• 9edo ear-training exercises by Alex Ness.