10edo
| ← 9edo | 10edo | 11edo → |
10 equal divisions of the octave (abbreviated 10edo or 10ed2), also called 10-tone equal temperament (10tet) or 10 equal temperament (10et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 10 equal parts of exactly 120 ¢ each. Each step represents a frequency ratio of 21/10, or the 10th root of 2.
Theory
10edo can be thought of as two circles of 5edo separated by 120 cents. It adds to 5edo a small neutral second (or large minor 2nd) and its inversion a large neutral seventh (or small major 7th); an excellent approximation of 13/8 and its inversion 16/13; and the familiar 600-cent tritone that appears in every even-numbered edo.
Taking the the 360 ¢ large neutral third as a generator produces a heptatonic moment of symmetry scale of the form 1 2 1 2 1 2 1 (3L 4s, or "mosh"), which is the most diatonic-like scale in 10edo excluding the 5edo degenerate diatonic scale, and can be seen as a neutralized diatonic scale.
It shares 5edo's approximation quality in the 2.3.7 subgroup (though the detuned fifth could be seen as a bigger problem with the more fine division of steps), but expands on its accuracy in the full 7-limit, by including a better approximation of 5/4 at 360 cents, resulting in the better tuning of various intervals including 5, such as 16/15 and 7/5. However, 6/5 is very poorly approximated, over 40 cents sharp, due to to the errors on 3/2 and 5/4 compounding. In fact, it is mapped to the exact same interval as 5/4, which results in the dicot exotemperament. So, if one wishes to represent JI with 10edo, it is best to use 5 carefully or not at all.
This third also serves as an extremely accurate approximation of 16/13, making 10edo usable as a 2.3.5.7.13 temperament, in which, alongside 5edo's temperaments in 2.3.7, septimal supermajor intervals are equated with tridecimal ultramajor intervals (tempering out 105/104), and 5-limit major and minor thirds are equated as mentioned before (tempering out 25/24). Additionally, 5-limit augmented and diminished intervals are equated with nearby septimal intervals (tempering out 225/224), and from this it can be seen that the syntonic comma is mapped to 120 cents. More accurately, it can be seen as a 2.7.13.15 temperament, restricting the 3.5 subgroup to powers of 15.
By treating 360c as 11/9, we arrive at 11/8 = 600c (tempering out 144/143), which allows 10edo to be treated as a full 13-limit temperament. However, it is more accurate to the no-11 subgroup.
10edo is a zeta peak edo, due to its decent tuning of the harmonics 2, 3, 5, 7, 13, and 17. 10edo is also the smallest edo that maintains 25% or lower relative error on all of the first eight harmonics of the harmonic series.
Thanks to its sevenths, 10edo is an ideal tuning for its size for metallic harmony.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +18.0 | -26.3 | -8.8 | +48.7 | -0.5 | +15.0 | -57.5 | -28.3 | +50.4 | +55.0 |
| Relative (%) | +0.0 | +15.0 | -21.9 | -7.4 | +40.6 | -0.4 | +12.5 | -47.9 | -23.6 | +42.0 | +45.8 | |
| Steps (reduced) |
10 (0) |
16 (6) |
23 (3) |
28 (8) |
35 (5) |
37 (7) |
41 (1) |
42 (2) |
45 (5) |
49 (9) |
50 (0) | |
Intervals
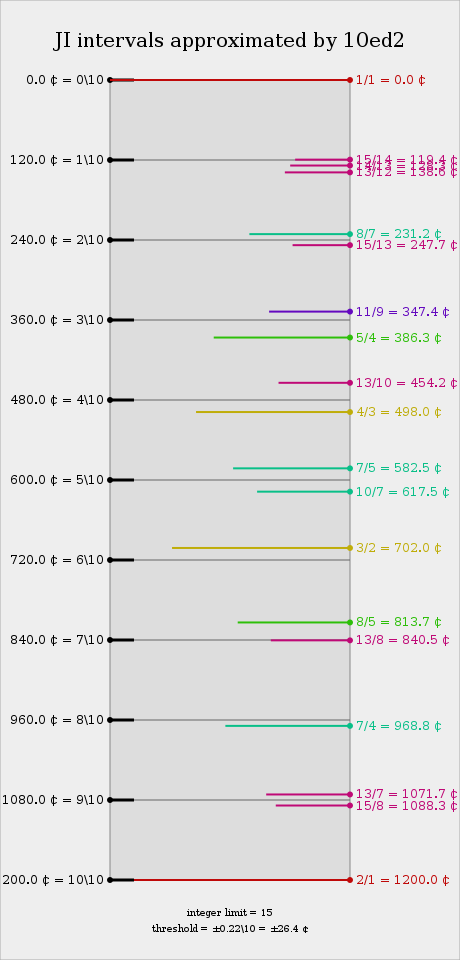
| Degree | Cents | Approximate ratios[note 1] | Additional ratios of 3, 5, and 9[note 2] |
Interval names | Ups and downs notation (EUs: vvA1 and m2) |
Audio | ||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1/1 | 256/243, 50/49, 25/24 | unison | unison, min 2nd | P1, m2 | D, Eb | |
| 1 | 120 | 16/15, 15/14, 14/13 | 10/9, 13/12, 81/80 | neutral second | mid 2nd | ~2 | ^D, vE | |
| 2 | 240 | 8/7, 15/13, 144/125, 224/195 | 9/8, 7/6 | hemifourth, major second, minor third | maj 2nd, min 3rd | M2, m3 | E, F | |
| 3 | 360 | 16/13 | 5/4 | neutral third | mid 3rd | ~3 | ^F, vG | |
| 4 | 480 | 64/49, 169/128 | 4/3, 9/7, 13/10 | perfect fourth | maj 3rd, perf 4th | M3, P4 | F#, G | |
| 5 | 600 | 91/64, 128/91, 169/120, 240/169 | 7/5, 10/7, 13/9, 18/13 | hemioctave, tritone | up 4th, down 5th | ^4, v5 | ^G, vA | |
| 6 | 720 | 49/32, 256/169 | 3/2, 14/9, 20/13 | perfect fifth | perf 5th, min 6th | P5, m6 | A, Bb | |
| 7 | 840 | 13/8 | 8/5 | neutral sixth | mid 6th | ~6 | ^A, vB | |
| 8 | 960 | 7/4, 26/15, 125/72, 195/112 | 16/9, 12/7 | hemitwelfth, major sixth, minor seventh | maj 6th, min 7th | M6, m7 | B, C | |
| 9 | 1080 | 15/8, 28/15, 13/7 | 9/5, 24/13, 160/81 | neutral seventh | mid 7th | ~7 | ^C, vD | |
| 10 | 1200 | 2/1 | 243/128, 49/25, 48/25 | octave | maj 7th, octave | M7, P8 | C#, D | |
Notation
Ups and downs notation
The interval table above shows the diatonic notation, generated by 5ths (6\10, representing 3/2). Alternative notations include pentatonic fifth-generated and heptatonic 3rd-generated.
Pentatonic 5th-generated
D * E * G * A * C * D (generator = 3/2 = 6\10 = perfect 5thoid)
D - D^/Ev - E - E^/Gv - G - G^/Av - A - A^/Cv - C - C^/Dv - D
1 - ^1/vs3 - s3 - ^s3/v4d - 4d - ^4d/v5d - 5d - ^5d/vs7 - s7 - ^s7/v8d - 8d (s = sub-, d = -oid)
pentatonic circles of fifths: ...D - A - E - C - G - D... and ...^D - ^A - ^E - ^C - ^G - ^D... (or equivalently ...vD - vA - vE - vC - vG - vD...)
pentatonic circles of fifths: ...1 - 5d - s3 - s7 - 4d - 1... and ...^1 - ^5d - ^s3 - ^s7 - ^4d - ^1... (or equivalently ...v1 - v5d - vs3 - vs7 - v4d - v1...)
(s- = sub-, -d = -oid, see 5edo notation)
Enharmonic unison: vvs3
Heptatonic 3rd-generated
D E * F G * A B * C D (generator = 3\10 = perfect 3rd)
D - E - E#/Fb - F - G - G#/Ab - A - B - B#/Cb - C - D
P1 - m2 - M2 - P3 - m4 - M4/m5 - M5 - P6 - m7 - M7 - P8
genchain of 3rds: ...Db - Fb - Ab - Cb - E - G - B - D - F - A - C - E# - G# - B# - D#... ("Every good boy deserves fudge and candy")
genchain of 3rds: ...d8 - d3 - m5 - m7 - m2 - m4 - P6 - P1 - P3 - M5 - M7 - M2 - M4 - A6 - A1...
See below: 3L 4s mosh notation
3L 4s (mosh) notation
See above: Heptatonic 3rd-generated notation.
The notation of Neutral[7]. Notes are denoted as LsLssLs = CDEFGABC, and raising and lowering by a chroma (L − s), 1 step in this instance, is denoted by ♯ and ♭.
| # | Cents | Note | Name | Associated ratios |
|---|---|---|---|---|
| 0 | 0 | C | Perf 1sn | 1/1 |
| 1 | 120 | Db | Min 2nd | 12/11 |
| 2 | 240 | D, Eb | Maj 2nd, dim 3rd | 9/8, 32/27 |
| 3 | 360 | E | Perf 3rd | 11/9, 27/22 |
| 4 | 480 | Fb | Min 4th | 4/3 |
| 5 | 600 | F, Gb | Maj 4th, min 5th | 11/8, 16/11 |
| 6 | 720 | G | Maj 5th | 3/2 |
| 7 | 840 | A | Perf 6th | 18/11, 44/27 |
| 8 | 960 | A#, Bb | Aug 6th, min 7th | 16/9, 27/16 |
| 9 | 1080 | B | Maj 7th | 11/6 |
| 10 | 1200 | C | Perf 8ve | 2/1 |
Sagittal notation
This notation is a subset of the notations for edos 20 and 30 and a superset of the notation for 5edo.
Evo and Revo flavors

Evo-SZ flavor

Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is identical to Stein–Zimmerman notation.
Approximation to JI
Selected just intervals by error
Selected 13-limit intervals
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 26zpi | 10.008456 | 119.89861 | 4.477141 | 4.464866 | 1.082282 | 14.181485 | 1198.986097 | −1.013903 | 8 | 5 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3.5 | 25/24, 256/243 | [⟨10 16 23]] | -0.089 | 9.27 | 7.73 |
| 2.3.5.7 | 25/24, 28/27, 49/48 | [⟨10 16 23 28]] | +0.718 | 8.15 | 6.79 |
| 2.3.5.7.13 | 25/24, 28/27, 40/39, 49/48 | [⟨10 16 23 28 37]] | +0.603 | 7.30 | 6.08 |
- 10et is lower in relative error than any previous equal temperaments in the 7- and 17-limit. The next equal temperaments doing better in those subgroups are 12 and 19eg, respectively.
- 10et is prominent in the 2.3.7.13, 2.3.5.7.13, 2.3.7.13.17, and 2.3.5.7.13.17 subgroup. The next equal temperaments doing better in those subgroups are 17, 19, 36 and 31, respectively.
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 9.7957 | 9.8637 | 10eff | ⟨10 16 23 28 34 36] |
| 9.8637 | 9.9727 | 10e | ⟨10 16 23 28 34 37] |
| 9.9727 | 10.1209 | 10 | ⟨10 16 23 28 35 37] |
| 10.1209 | 10.1339 | 10c | ⟨10 16 24 28 35 37] |
| 10.1339 | 10.1519 | 10cf | ⟨10 16 24 28 35 38] |
| 10.1519 | 10.2618 | 10cdf | ⟨10 16 24 29 35 38] |
Commas
10et tempers out the following commas. This assumes the val ⟨10 16 23 28 35 37].
| Prime limit |
Ratio[note 3] | Monzo | Cents | Color name | Name(s) |
|---|---|---|---|---|---|
| 3 | 256/243 | [8 -5⟩ | 90.22 | Sawa | Blackwood comma, Pythagorean limma |
| 5 | 25/24 | [-3 -1 2⟩ | 70.67 | Yoyo | Dicot comma, classic chroma |
| 5 | 16875/16384 | [-14 3 4⟩ | 51.12 | Laquadyo | Negri comma, double augmentation diesis |
| 5 | (16 digits) | [-25 7 6⟩ | 31.57 | Lala-tribiyo | Ampersand comma |
| 5 | 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma, Avicenna's enharmonic diesis |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.70 | Zozo | Semaphoresma, slendro diesis |
| 7 | 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Jubilisma, tritonic diesis |
| 7 | 686/675 | [1 -3 -2 3⟩ | 27.99 | Trizo-agugu | Senga |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma, Archytas' comma, Leipziger Komma |
| 7 | (18 digits) | [-10 7 8 -7⟩ | 22.41 | Lasepru-aquadbiyo | Blackjackisma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.43 | Latrizo | Gamelisma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Ruyoyo | Marvel comma, septimal kleisma |
| 7 | 16875/16807 | [0 3 4 -5⟩ | 6.99 | Quinru-aquadyo | Mirkwai comma |
| 7 | (24 digits) | [11 -10 -10 10⟩ | 5.57 | Saquinbizogu | Linus comma |
| 7 | 2401/2400 | [-5 -1 -2 4⟩ | 0.72 | Bizozogu | Breedsma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Luzozogu | Werckisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.21 | Lururuyo | Swetisma |
| 11 | 3025/3024 | [-4 -3 2 -1 2⟩ | 0.57 | Loloruyoyo | Lehmerisma |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap comma, biome comma |
| 13 | 196/195 | [2 -1 -1 2 0 -1⟩ | 8.86 | Thuzozogu | Mynucuma |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.56 | Bithogu | Island comma, parizeksma |
Rank-2 temperaments
| Periods per 8ve |
Generator | Temperament(s) |
|---|---|---|
| 1 | 1\10 | Negri, miracle (out-of-tune) |
| 1 | 3\10 | Dicot / beatles / neutral |
| 2 | 1\10 | Pajara (out-of-tune) |
| 2 | 2\10 | Decimal, lemba (out-of-tune) |
| 5 | 1\10 | Blackwood / blacksmith |
Scales
MOS scales
- Decimal/Lemba[6] 4L 2s (period = 5\10, gen = 2\10): 2 2 1 2 2 1
- Dicot[7] 3L 4s (gen = 3\10): 1 2 1 2 1 2 1
- Negri[9] 1L 8s (gen = 1\10): 1 1 1 1 2 1 1 1 1
Other scales
- Pinetone major pentatonic (subset of Dicot[7]): 2 1 3 1 3
- Pinetone minor pentatonic (subset of Dicot[7]): 3 1 2 3 1
- Marvel augmented hexatonic (subset of Dicot[7]): 2 1 3 1 2 1
- Marvel double harmonic hexatonic (subset of Dicot[7]): 1 2 1 3 2 1, 1 2 3 1 2 1
- Decimal/Lemba[6] 4M: 2 1 2 2 2 1
- Dicot[7] 4M: 2 1 1 2 2 1 1
Horagrams
Diagrams
Instruments
10edo lends itself exceptionally well to guitar (and other fretted strings), on account of the fact that five of its flat 4ths (at 480 ¢) exactly spans two octaves (480 × 5 = 2400), meaning the open strings can be uniformly tuned in 4ths. This allows for greater uniformity in chord and scale fingering patterns than in 12edo, making it exceptionally easy to learn. For instance, the fingering for an "E" chord would be 0 – 2 – 2 – 1 – 0 – 0 (low to high), an "A" chord would be 0 – 0 – 2 – 2 – 1 – 0, and a "D" chord would be 1, 0, 0, 2, 2, 1. This is also the case in all edos which are multiples of 5, but in 10-edo it is particularly simple.
Retuning a conventional keyboard to 10edo may be done in many ways, but neglecting or making redundant the Eb and Ab keys preserves the sLsLsLs scale on the white keys. Redundancy may make modulation easier, but another option is tuning the superfluous keys to selections from 20edo which approximates the 11th harmonic with relative accuracy, among other features.

|
| A Decaphonic (10edo) Classical Guitar |
Lumatone
See Lumatone mapping for 10edo.
Music
- See also: Category:10edo tracks
Notes
- ↑ Based on treating 10edo as a 2.15.7.13-subgroup temperament; other approaches are also possible.
- ↑ Adding the ratios of 3, 5, and 9 introduces greater error while giving several more harmonic identities to the 10-edo intervals
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.