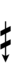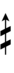30edo

← 29edo

30edo

31edo →

Prime factorization

2 × 3 × 5

Step size

40¢

Fifth

18\30 (720¢) (→3\5)

Semitones (A1:m2)

6:0 (240¢ : 0¢)

Dual sharp fifth

18\30 (720¢) (→3\5)

Dual flat fifth

17\30 (680¢)

Dual major 2nd

5\30 (200¢) (→1\6)

Consistency limit

5

Distinct consistency limit

5

30 equal divisions of the octave (abbreviated 30edo or 30ed2), also called 30-tone equal temperament (30tet) or 30 equal temperament (30et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 30 equal parts of exactly 40 ¢ each. Each step represents a frequency ratio of 2^1/30, or the 30th root of 2.

Theory

Approximation of odd harmonics in 30edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	+18.0	+13.7	-8.8	-3.9	+8.7	-0.5	-8.3	+15.0	-17.5	+9.2	+11.7
Error	Relative (%)	+45.1	+34.2	-22.1	-9.8	+21.7	-1.3	-20.7	+37.6	-43.8	+23.0	+29.3
Steps (reduced)		48 (18)	70 (10)	84 (24)	95 (5)	104 (14)	111 (21)	117 (27)	123 (3)	127 (7)	132 (12)	136 (16)

Its patent val is a doubled version of the patent val for 15edo through the 11-limit, so 30 can be viewed as a contorted version of 15. In the 13-limit it supplies the optimal patent val for quindecic temperament.

A plot of the Z function around 30.

However, 5\30 is 200 cents, which is a good (and familiar) approximation for 9/8, and hence 30edo can be viewed inconsistently, as having a 9/1 at 95\30 as well as 96\30.

Instead of the 18\30 fifth of 720 cents, 30edo also makes available a 17\30 fifth of 680 cents. This is an ideal tuning for pelogic (5-limit mavila), which tempers out 135/128. When 30edo is used for pelogic, 5\30 can again be used inconsistently as a 9/8.

Subsets and supersets

30edo has subset edos 1, 2, 3, 5, 6, 10, 15 and it is a largely composite edo.

30edo is the 3rd primorial edo, being the product of first three primes and thus the smallest number with three distinct prime factors. As a corollary, 30edo is the smallest EDO that supports perfectly balanced scales that are minimal and not equally spaced. See the article on perfect balance.

Intervals

Step	Cents	Ups and downs notation			Armodue Notation
0	0	P1	unison, minor 2nd	D, Eb	1
1	40	^1, ^m2	up unison, upminor 2nd	^D, ^Eb	2b
2	80	^^1, v~2	dup unison, downmid 2nd	^^D, ^^Eb	9#
3	120	~2	mid 2nd	v3E	1#
4	160	^~2	upmid 2nd	vvE	2
5	200	vM2	downmajor 2nd	vE	3b
6	240	M2, m3	major 2nd, minor 3rd	E, F	1x, 4bb
7	280	^m3	upminor 3rd	^F	2#
8	320	v~3	downmid 3rd	^^F	3
9	360	~3	mid 3rd	^3F, v3F#	4b
10	400	^~3	upmid 3rd	vvF#	5b
11	440	vM3, v4	downmajor 3rd, down 4th	vF#, vG	3#
12	480	M3, P4	major 3rd, perfect 4th	F#, G	4
13	520	^4	up 4th	^G	5
14	560	v~4, v~d5	downmid 4th, downmid 5th	^^G, ^^Ab	6b
15	600	~4, ~5	mid 4th, mid 5th	^3G, v3A	4#
16	640	^~4, ^~5	upmid 4th, upmid 5th	vvG#, vvA	5#
17	680	v5	down 5th	vA	6
18	720	P5, m6	perfect 5th, minor 6th	A, Bb	7b
19	760	^5, ^m6	up 5th, upminor 6th	^A, ^Bb	5x, 8bb
20	800	v~6	downmid 6th	^^Bb	6#
21	840	~6	mid 6th	v3B	7
22	880	^~6	upmid 6th	vvB	8b
23	920	vM6	downmajor 6th	vB	6x, 9bb
24	960	M6. m7	major 6th, minor 7th	B, C	7#
25	1000	^m7	upminor 7th	^C	8
26	1040	v~7	downmid 7th	^^C	9b
27	1080	~7	mid 7th	^3C	1b
28	1120	^~7, vv8	upmid 7th, dud 8ve	vvC#, vvD	8#
29	1160	vM7, v8	downmajor 7th, down 8ve	vC#, vD	9
30	1200	P8	major 7th, 8ve	C#, D	1

Commas

30 EDO tempers out the following commas. (Note: This assumes the val ⟨30 48 70 84 104 111].)

Prime Limit	Ratio^[1]	Monzo	Cents	Color name	Name(s)
3	256/243	[8 -5⟩	90.22	Sawa	Limma, Pythagorean minor second
5	250/243	[1 -5 3⟩	49.17	Triyo	Maximal diesis, Porcupine comma
5	128/125	[7 0 -3⟩	41.06	Trigu	Diesis, augmented comma
5	15625/15552	[-6 -5 6⟩	8.11	Tribiyo	Kleisma, semicomma majeur
7	1029/1000	[-3 1 -3 3⟩	49.49	Trizogu	Keega
7	49/48	[-4 -1 0 2⟩	35.70	Zozo	Slendro diesis
7	64/63	[6 -2 0 -1⟩	27.26	Ru	Septimal comma, Archytas' comma, Leipziger Komma
7	64827/64000	[-9 3 -3 4⟩	22.23	Laquadzo-atrigu	Squalentine
7	875/864	[-5 -3 3 1⟩	21.90	Zotriyo	Keema
7	126/125	[1 2 -3 1⟩	13.79	Zotrigu	Septimal semicomma, Starling comma
7	4000/3969	[5 -4 3 -2⟩	13.47	Rurutriyo	Octagar
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	6144/6125	[11 1 -3 -2⟩	5.36	Saruru-atrigu	Porwell
7	(12 digits)	[-4 6 -6 3⟩	0.33	Trizogugu	Landscape comma
11	100/99	[2 -2 2 0 -1⟩	17.40	Luyoyo	Ptolemisma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
11	176/175	[4 0 -2 -1 1⟩	9.86	Lorugugu	Valinorsma
11	65536/65219	[16 0 0 -2 -3⟩	8.39	Satrilu-aruru	Orgonisma
11	385/384	[-7 -1 1 1 1⟩	4.50	Lozoyo	Keenanisma
11	441/440	[-3 2 -1 2 -1⟩	3.93	Luzozogu	Werckisma
11	4000/3993	[5 -1 3 0 -3⟩	3.03	Triluyo	Wizardharry
11	3025/3024	[-4 -3 2 -1 2⟩	0.57	Loloruyoyo	Lehmerisma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Rank-2 temperaments

As 30edo is largely composite, only 7, 11 and 13 steps create MOS scales that cover every interval using one period per octave.

7/30 produces Lovecraft, in which 2 generators is a moderately sharp 11/8, 3 a near perfect 13/8 and 5 the familiar mildly flat 9/8 from 12edo, creating the possibility of ignoring the 3rd & 5th entirely to use those harmonics as the primary building blocks of harmony in a similar way to orgone.

11 produces a flat sensi scale. 13 is an excellent higher order Mavila tuning that functions the closest to the familiar diatonic scale you can get in this edo.

Scales

MOS scales

Lovecraft[5] - 77772
Lovecraft[9] - 525252522
Lovecraft[13] - 3223223223222
Lovecraft[17] - 22221222122212221
Sensi[5] - 83838
Sensi[8] - 53353353
Sensi[11] - 33323332332
Sensi[19] - 2121212212121221212
Mavila[5] - 94944
Mavila[7] - 5445444
Mavila[9] - 444414441
Mavila[16] - 3131313113131311
Mavila[23] - 21121121121112112112111

Subsets of Mavila[16]

Arcade (approximated from 32afdo): 9 3 5 8 5
Blackened skies (approximated from Compton in 72edo): 8 5 2 3 2 8 2
Carousel (this is the original/default tuning): 9 4 4 9 4
Dewdrops (this is the original/default tuning): 4 4 4 5 4 4 5
Geode (approximated from 6afdo): 7 6 4 9 4
Lost spirit (approximated from Meantone in 31edo): 7 5 2 3 5 3 5
Lost phantom (this is the original/default tuning): 8 5 2 2 6 2 5
Mechanical (approximated from 16afdo): 7 2 8 8 5
Mushroom (approximated from 30afdo): 7 5 5 3 10
Nightdrive (this is the original/default tuning): 8 5 4 9 4
Pelagic (this is the original/default tuning): 8 4 2 4 7 5
Bathypelagic (this is the original/default tuning): 8 4 2 3 8 5
Underpass (approximated from 10afdo): 8 9 5 3 5
Volcanic (approximated from 16afdo): 3 6 8 8 5

Subsets of 15edo

Augmented[6] MOS: 8 2 8 2 8 2
Equipentatonic (exact from 5edo): 6 6 6 6 6
Rockpool (approximated from 47zpi): 2 8 2 6 6 6

Other notable scales

Approximation of Pelog lima: 3 4 10 3 10
Amiot scale

Delta-rational harmony

The tables below show chords that approximate 3-integer-limit delta-rational chords with least-squares error less than 0.001.

Fully delta-rational triads

chord	delta signature	error
0,1,2	+1+1	0.00026
0,1,3	+1+2	0.00058
0,1,4	+1+3	0.00094
0,2,3	+2+1	0.00047
0,3,4	+3+1	0.00068
0,3,11	+1+3	0.00064
0,4,11	+1+2	0.00039
0,5,8	+3+2	0.00057
0,6,16	+1+2	0.00042
0,7,13	+1+1	0.00035
0,7,23	+1+3	0.00024
0,10,25	+1+2	0.00072
0,11,17	+3+2	0.00063
0,11,27	+1+2	0.00072
0,13,23	+1+1	0.00030
0,14,29	+2+3	0.00019
0,15,19	+3+1	0.00069
0,20,25	+3+1	0.00085

Partially delta-rational tetrads

chord	delta signature	error
0,1,2,3	+1+?+1	0.00064
0,1,3,4	+1+?+1	0.00097
0,1,15,16	+2+?+3	0.00097
0,1,15,17	+1+?+3	0.00098
0,1,16,17	+2+?+3	0.00060
0,1,16,18	+1+?+3	0.00050
0,1,17,18	+2+?+3	0.00021
0,1,17,19	+1+?+3	0.00002
0,1,18,19	+2+?+3	0.00018
0,1,18,20	+1+?+3	0.00047
0,1,19,20	+2+?+3	0.00058
0,1,19,21	+1+?+3	0.00098
0,1,20,21	+2+?+3	0.00099
0,1,28,29	+1+?+2	0.00086
0,2,3,4	+2+?+1	0.00094
0,2,6,11	+1+?+3	0.00036
0,2,7,12	+1+?+3	0.00063
0,2,11,12	+3+?+2	0.00089
0,2,11,14	+1+?+2	0.00084
0,2,12,13	+3+?+2	0.00044
0,2,12,15	+1+?+2	0.00005
0,2,13,14	+3+?+2	0.00002
0,2,13,16	+1+?+2	0.00095
0,2,14,15	+3+?+2	0.00049
0,2,15,16	+3+?+2	0.00098
0,2,16,20	+1+?+3	0.00053
0,2,17,19	+2+?+3	0.00043
0,2,17,21	+1+?+3	0.00046
0,2,18,20	+2+?+3	0.00036
0,3,4,8	+2+?+3	0.00071
0,3,5,9	+2+?+3	0.00050
0,3,7,12	+1+?+2	0.00017
0,3,9,16	+1+?+3	0.00024
0,3,16,22	+1+?+3	0.00003
0,3,17,18	+2+?+1	0.00085
0,3,17,19	+1+?+1	0.00100
0,3,17,20	+2+?+3	0.00066
0,3,17,21	+1+?+2	0.00006
0,3,18,19	+2+?+1	0.00031
0,3,18,20	+1+?+1	0.00005
0,3,18,21	+2+?+3	0.00055
0,3,19,20	+2+?+1	0.00025
0,3,19,21	+1+?+1	0.00092
0,3,20,21	+2+?+1	0.00081
0,3,24,29	+1+?+3	0.00063
0,4,5,15	+1+?+3	0.00038
0,4,7,12	+2+?+3	0.00062
0,4,10,19	+1+?+3	0.00023
0,4,11,17	+1+?+2	0.00078
0,4,12,13	+3+?+1	0.00099
0,4,13,14	+3+?+1	0.00049
0,4,13,15	+3+?+2	0.00044
0,4,13,16	+1+?+1	0.00005
0,4,14,15	+3+?+1	0.00002
0,4,14,16	+3+?+2	0.00052
0,4,15,16	+3+?+1	0.00054
0,4,17,21	+2+?+3	0.00089
0,4,18,22	+2+?+3	0.00074
0,4,20,25	+1+?+2	0.00030
0,4,22,29	+1+?+3	0.00041
0,5,6,9	+3+?+2	0.00051
0,5,6,18	+1+?+3	0.00011
0,5,8,16	+1+?+2	0.00028
0,5,9,15	+2+?+3	0.00030
0,5,10,14	+1+?+1	0.00027
0,5,10,21	+1+?+3	0.00084
0,5,11,13	+2+?+1	0.00017
0,5,12,14	+2+?+1	0.00078
0,5,14,21	+1+?+2	0.00095
0,5,15,25	+1+?+3	0.00006
0,5,18,23	+2+?+3	0.00093
0,5,20,29	+1+?+3	0.00014
0,5,22,28	+1+?+2	0.00093
0,5,23,24	+3+?+1	0.00073
0,5,23,25	+3+?+2	0.00075
0,5,23,26	+1+?+1	0.00020
0,5,24,25	+3+?+1	0.00009
0,5,24,26	+3+?+2	0.00045
0,5,25,26	+3+?+1	0.00057
0,6,7,21	+1+?+3	0.00086
0,6,8,13	+1+?+1	0.00079
0,6,10,17	+2+?+3	0.00091
0,6,11,20	+1+?+2	0.00026
0,6,14,17	+3+?+2	0.00003
0,6,19,21	+2+?+1	0.00066
0,6,19,23	+1+?+1	0.00086
0,6,20,22	+2+?+1	0.00048
0,7,8,11	+2+?+1	0.00095
0,7,8,12	+3+?+2	0.00035
0,7,9,11	+3+?+1	0.00020
0,7,9,12	+2+?+1	0.00039
0,7,10,12	+3+?+1	0.00074
0,7,11,19	+2+?+3	0.00075
0,7,13,23	+1+?+2	0.00005
0,7,14,28	+1+?+3	0.00034
0,7,16,21	+1+?+1	0.00097
0,7,18,27	+1+?+2	0.00030
0,7,21,24	+3+?+2	0.00028
0,7,27,29	+2+?+1	0.00032
0,8,10,27	+1+?+3	0.00088
0,8,12,21	+2+?+3	0.00022
0,8,14,18	+3+?+2	0.00099
0,8,15,17	+3+?+1	0.00054
0,8,15,18	+2+?+1	0.00001
0,8,16,18	+3+?+1	0.00053
0,8,22,27	+1+?+1	0.00033
0,9,10,15	+3+?+2	0.00013
0,9,10,29	+1+?+3	0.00029
0,9,12,19	+1+?+1	0.00028
0,9,12,25	+1+?+2	0.00000
0,9,16,28	+1+?+2	0.00005
0,9,19,25	+1+?+1	0.00028
0,9,20,24	+3+?+2	0.00025
0,9,21,23	+3+?+1	0.00015
0,9,21,24	+2+?+1	0.00068
0,10,13,17	+2+?+1	0.00052
0,10,13,24	+2+?+3	0.00042
0,10,15,20	+3+?+2	0.00006
0,10,17,24	+1+?+1	0.00005
0,10,25,29	+3+?+2	0.00048
0,10,26,28	+3+?+1	0.00028
0,10,26,29	+2+?+1	0.00061
0,11,13,16	+3+?+1	0.00032
0,11,17,21	+2+?+1	0.00085
0,11,20,25	+3+?+2	0.00095
0,12,14,23	+1+?+1	0.00005
0,12,17,20	+3+?+1	0.00014
0,12,22,26	+2+?+1	0.00081
0,12,24,29	+3+?+2	0.00014
0,13,18,27	+1+?+1	0.00000
0,13,21,24	+3+?+1	0.00013
0,14,16,23	+3+?+2	0.00035
0,14,19,24	+2+?+1	0.00067
0,14,25,28	+3+?+1	0.00040
0,15,23,28	+2+?+1	0.00083
0,16,19,23	+3+?+1	0.00076
0,17,20,28	+3+?+2	0.00099
0,17,21,27	+2+?+1	0.00067
0,17,22,26	+3+?+1	0.00042
0,18,25,29	+3+?+1	0.00042
0,19,20,29	+3+?+2	0.00033
0,21,23,28	+3+?+1	0.00012