72edo
| ← 71edo | 72edo | 73edo → |
72 equal divisions of the octave (abbreviated 72edo or 72ed2), also called 72-tone equal temperament (72tet) or 72 equal temperament (72et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 72 equal parts of about 16.7 ¢ each. Each step represents a frequency ratio of 21/72, or the 72nd root of 2.
Each step of 72edo is called a morion (plural moria). This produces a twelfth-tone tuning, with the whole tone measuring 200 ¢, the same as in 12edo. 72edo is also a superset of 24edo, a common and standard tuning of Arabic music, and has itself been used to tune Turkish music.
Composers that used 72edo include Ivan Wyschnegradsky, Julián Carrillo (who is better associated with 96edo), Georg Friedrich Haas, Ezra Sims, Rick Tagawa, James Tenney, and the jazz musician Joe Maneri.
Theory
72edo approximates 11-limit just intonation exceptionally well. It is consistent in the 17-odd-limit and is the ninth zeta integral edo. It is the second edo (after 58) to be distinctly consistent in the 11-odd-limit, the first edo to be consistent to distance 2 in the 11-odd-limit, and the first edo to be consistent in the 12- and 13-odd-prime-sum-limit.
The octave, fifth and fourth are the same size as they would be in 12edo, 72, 42 and 30 steps respectively, but the classic major third (5/4) measures 23 steps, not 24, and other 5-limit major intervals are one step flat of 12edo while minor ones are one step sharp. The septimal minor seventh (7/4) is 58 steps, while the undecimal semiaugmented fourth (11/8) is 33.
72et is the only 11-limit regular temperament which treats harmonics 24 to 28 as being equidistant in pitch, splits 25/24 into two equal 49/48~50/49's, and splits 28/27 into two equal 55/54~56/55's. It is also an excellent tuning for miracle temperament, especially the 11-limit version, and the related rank-3 temperament prodigy, and is a good tuning for other temperaments and scales, including wizard, harry, catakleismic, compton, unidec and tritikleismic.
The 13th harmonic (octave reduced) is so closely mapped on acoustic phi that 72edo could be treated as a 2.3.5.7.11.ϕ.17 temperament.
72edo is the smallest multiple of 12edo that (just barely) has another diatonic fifth, 43\72, an extremely hard diatonic fifth suitable for a 5edo circulating temperament.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -1.96 | -2.98 | -2.16 | -1.32 | -7.19 | -4.96 | +2.49 | +5.06 |
| Relative (%) | +0.0 | -11.7 | -17.9 | -13.0 | -7.9 | -43.2 | -29.7 | +14.9 | +30.4 | |
| Steps (reduced) |
72 (0) |
114 (42) |
167 (23) |
202 (58) |
249 (33) |
266 (50) |
294 (6) |
306 (18) |
326 (38) | |
| Harmonic | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.76 | +4.96 | -1.34 | +4.27 | +5.15 | +1.16 | -6.84 | +7.50 | -0.22 |
| Relative (%) | +22.5 | +29.8 | -8.1 | +25.6 | +30.9 | +7.0 | -41.0 | +45.0 | -1.3 | |
| Steps (reduced) |
350 (62) |
357 (69) |
375 (15) |
386 (26) |
391 (31) |
400 (40) |
412 (52) |
424 (64) |
427 (67) | |
Octave stretch
72edo's approximations of harmonics 3, 5, 7, 11, 13 and 17 can all be improved by slightly stretching the octave, using tunings such as 114edt or 186ed6. 114edt is quite hard and might be best for the 13- or 17-limit specifically. 186ed6 is milder and less disruptive, suitable for 11-limit and/or full 19-limit harmonies.
Subsets and supersets
Since 72 factors into primes as 23 × 32, 72edo has subset edos 2, 3, 4, 6, 8, 9, 12, 18, 24, and 36. 144edo, which doubles it, provides a possible correction to its approximate harmonic 13.
Intervals
| # | Cents | Approximate ratios[note 1] | Ups and downs notation | SKULO interval names and notation | (K, S, U) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1/1 | P1 | perfect unison | D | P1 | perfect unison | D | D |
| 1 | 16.7 | 81/80, 91/90, 99/98, 100/99, 105/104 | ^1 | up unison | ^D | K1, L1 | comma-wide unison, large unison | KD, LD | KD |
| 2 | 33.3 | 45/44, 49/48, 50/49, 55/54, 64/63 | ^^ | dup unison | ^^D | S1, O1 | super unison, on unison | SD, OD | SD |
| 3 | 50.0 | 33/32, 36/35, 40/39 | ^31, v3m2 | trup unison, trudminor 2nd | ^3D, v3Eb | U1, H1, hm2 | uber unison, hyper unison, hypominor 2nd | UD, HD, uEb | UD, uEb |
| 4 | 66.7 | 25/24, 26/25, 27/26, 28/27 | vvm2 | dudminor 2nd | vvEb | kkA1, sm2 | classic aug unison, subminor 2nd | kkD#, sEb | sD#, (kkD#), sEb |
| 5 | 83.3 | 20/19, 21/20, 22/21 | vm2 | downminor 2nd | vEb | kA1, lm2 | comma-narrow aug unison, little minor 2nd | kD#, lEb | kD#, kEb |
| 6 | 100.0 | 17/16, 18/17, 19/18 | m2 | minor 2nd | Eb | m2 | minor 2nd | Eb | Eb |
| 7 | 116.7 | 15/14, 16/15 | ^m2 | upminor 2nd | ^Eb | Km2 | classic minor 2nd | KEb | KEb |
| 8 | 133.3 | 13/12, 14/13, 27/25 | ^^m2, v~2 | dupminor 2nd, downmid 2nd | ^^Eb | Om2 | on minor 2nd | OEb | SEb |
| 9 | 150.0 | 12/11 | ~2 | mid 2nd | v3E | N2 | neutral 2nd | UEb/uE | UEb/uE |
| 10 | 166.7 | 11/10 | ^~2, vvM2 | upmid 2nd, dudmajor 2nd | vvE | oM2 | off major 2nd | oE | sE |
| 11 | 183.3 | 10/9 | vM2 | downmajor 2nd | vE | kM2 | classic/comma-narrow major 2nd | kE | kE |
| 12 | 200.0 | 9/8 | M2 | major 2nd | E | M2 | major 2nd | E | E |
| 13 | 216.7 | 17/15, 25/22 | ^M2 | upmajor 2nd | ^E | LM2 | large major 2nd | LE | KE |
| 14 | 233.3 | 8/7 | ^^M2 | dupmajor 2nd | ^^E | SM2 | supermajor 2nd | SE | SE |
| 15 | 250.0 | 15/13, 22/19 | ^3M2, v3m3 |
trupmajor 2nd, trudminor 3rd |
^3E, v3F |
HM2, hm3 | hypermajor 2nd, hypominor 3rd | HE, hF | UE, uF |
| 16 | 266.7 | 7/6 | vvm3 | dudminor 3rd | vvF | sm3 | subminor 3rd | sF | sF |
| 17 | 283.3 | 13/11, 20/17 | vm3 | downminor 3rd | vF | lm3 | little minor 3rd | lF | kF |
| 18 | 300.0 | 19/16, 25/21, 32/27 | m3 | minor 3rd | F | m3 | minor 3rd | F | F |
| 19 | 316.7 | 6/5 | ^m3 | upminor 3rd | ^F | Km3 | classic minor 3rd | KF | KF |
| 20 | 333.3 | 17/14, 39/32, 40/33 | ^^m3, v~3 | dupminor 3rd, downmid 3rd | ^^F | Om3 | on minor third | OF | SF |
| 21 | 350.0 | 11/9, 27/22 | ~3 | mid 3rd | ^3F | N3 | neutral 3rd | UF/uF# | UF/uF# |
| 22 | 366.7 | 16/13, 21/17, 26/21 | ^~3, vvM3 | upmid 3rd, dudmajor 3rd | vvF# | oM3 | off major 3rd | oF# | sF# |
| 23 | 383.3 | 5/4 | vM3 | downmajor 3rd | vF# | kM3 | classic major 3rd | kF# | kF# |
| 24 | 400.0 | 24/19 | M3 | major 3rd | F# | M3 | major 3rd | F# | F# |
| 25 | 416.7 | 14/11 | ^M3 | upmajor 3rd | ^F# | LM3 | large major 3rd | LF# | KF# |
| 26 | 433.3 | 9/7 | ^^M3 | dupmajor 3rd | ^^F# | SM3 | supermajor 3rd | SF# | SF# |
| 27 | 450.0 | 13/10, 22/17 | ^3M3, v34 | trupmajor 3rd, trud 4th | ^3F#, v3G | HM3, h4 | hypermajor 3rd, hypo 4th | HF#, hG | UF#, uG |
| 28 | 466.7 | 17/13, 21/16 | vv4 | dud 4th | vvG | s4 | sub 4th | sG | sG |
| 29 | 483.3 | 33/25 | v4 | down 4th | vG | l4 | little 4th | lG | kG |
| 30 | 500.0 | 4/3 | P4 | perfect 4th | G | P4 | perfect 4th | G | G |
| 31 | 516.7 | 27/20 | ^4 | up 4th | ^G | K4 | comma-wide 4th | KG | KG |
| 32 | 533.3 | 15/11, 19/14, 26/19 | ^^4, v~4 | dup 4th, downmid 4th | ^^G | O4 | on 4th | OG | SG |
| 33 | 550.0 | 11/8 | ~4 | mid 4th | ^3G | U4/N4 | uber 4th / neutral 4th | UG | UG |
| 34 | 566.7 | 18/13, 25/18 | ^~4, vvA4 | upmid 4th, dudaug 4th | vvG# | kkA4, sd5 | classic aug 4th, sub dim 5th | kkG#, sAb | SG#, (kkG#), sAb |
| 35 | 583.3 | 7/5 | vA4, vd5 | downaug 4th, downdim 5th |
vG#, vAb | kA4, ld5 | comma-narrow aug 4th, little dim 5th | kG#, lAb | kG#, kAb |
| 36 | 600.0 | 17/12, 24/17 | A4, d5 | aug 4th, dim 5th | G#, Ab | A4, d5 | aug 4th, dim 5th | G#, Ab | G#, Ab |
| 37 | 616.7 | 10/7 | ^A4, ^d5 | upaug 4th, updim 5th | ^G#, ^Ab | LA4, Kd5 | large aug 4th, comma-wide dim 5th | LG#, KAb | KG#, KAb |
| 38 | 633.3 | 13/9, 36/25 | v~5, ^^d5 | downmid 5th, dupdim 5th |
^^Ab | SA4, KKd5 | super aug 4th, classic dim 5th | SG#, KKAb | SG#, SAb, (KKAb) |
| 39 | 650.0 | 16/11 | ~5 | mid 5th | v3A | u5/N5 | unter 5th / neutral 5th | uA | uA |
| 40 | 666.7 | 19/13, 22/15, 28/19 | vv5, ^~5 | dud 5th, upmid 5th | vvA | o5 | off 5th | oA | sA |
| 41 | 683.3 | 40/27 | v5 | down 5th | vA | k5 | comma-narrow 5th | kA | kA |
| 42 | 700.0 | 3/2 | P5 | perfect 5th | A | P5 | perfect 5th | A | A |
| 43 | 716.7 | 50/33 | ^5 | up 5th | ^A | L5 | large fifth | LA | KA |
| 44 | 733.3 | 26/17, 32/21 | ^^5 | dup 5th | ^^A | S5 | super fifth | SA | SA |
| 45 | 750.0 | 17/11, 20/13 | ^35, v3m6 | trup 5th, trudminor 6th | ^3A, v3Bb | H5, hm6 | hyper fifth, hypominor 6th | HA, hBb | UA, uBb |
| 46 | 766.7 | 14/9 | vvm6 | dudminor 6th | vvBb | sm6 | superminor 6th | sBb | sBb |
| 47 | 783.3 | 11/7 | vm6 | downminor 6th | vBb | lm6 | little minor 6th | lBb | kBb |
| 48 | 800.0 | 19/12 | m6 | minor 6th | Bb | m6 | minor 6th | Bb | Bb |
| 49 | 816.7 | 8/5 | ^m6 | upminor 6th | ^Bb | Km6 | classic minor 6th | kBb | kBb |
| 50 | 833.3 | 13/8, 21/13, 34/21 | ^^m6, v~6 | dupminor 6th, downmid 6th | ^^Bb | Om6 | on minor 6th | oBb | sBb |
| 51 | 850.0 | 18/11, 44/27 | ~6 | mid 6th | v3B | N6 | neutral 6th | UBb, uB | UBb, uB |
| 52 | 866.7 | 28/17, 33/20, 64/39 | ^~6, vvM6 | upmid 6th, dudmajor 6th | vvB | oM6 | off major 6th | oB | sB |
| 53 | 883.3 | 5/3 | vM6 | downmajor 6th | vB | kM6 | classic major 6th | kB | kB |
| 54 | 900.0 | 27/16, 32/19, 42/25 | M6 | major 6th | B | M6 | major 6th | B | B |
| 55 | 916.7 | 17/10, 22/13 | ^M6 | upmajor 6th | ^B | LM6 | large major 6th | LB | KB |
| 56 | 933.3 | 12/7 | ^^M6 | dupmajor 6th | ^^B | SM6 | supermajor 6th | SB | SB |
| 57 | 950.0 | 19/11, 26/15 | ^3M6, v3m7 |
trupmajor 6th, trudminor 7th |
^3B, v3C |
HM6, hm7 | hypermajor 6th, hypominor 7th | HB, hC | UB, uC |
| 58 | 966.7 | 7/4 | vvm7 | dudminor 7th | vvC | sm7 | subminor 7th | sC | sC |
| 59 | 983.3 | 30/17, 44/25 | vm7 | downminor 7th | vC | lm7 | little minor 7th | lC | kC |
| 60 | 1000.0 | 16/9 | m7 | minor 7th | C | m7 | minor 7th | C | C |
| 61 | 1016.7 | 9/5 | ^m7 | upminor 7th | ^C | Km7 | classic/comma-wide minor 7th | KC | KC |
| 62 | 1033.3 | 20/11 | ^^m7, v~7 | dupminor 7th, downmid 7th | ^^C | Om7 | on minor 7th | OC | SC |
| 63 | 1050.0 | 11/6 | ~7 | mid 7th | ^3C | N7, hd8 | neutral 7th, hypo dim 8ve | UC/uC#, hDb | UC/uC#, uDb |
| 64 | 1066.7 | 13/7, 24/13, 50/27 | ^~7, vvM7 | upmid 7th, dudmajor 7th | vvC# | oM7, sd8 | off major 7th, sub dim 8ve | oC#, sDb | sC#, sDb |
| 65 | 1083.3 | 15/8, 28/15 | vM7 | downmajor 7th | vC# | kM7, ld8 | classic major 7th, little dim 8ve | kC#, lDb | kC#, kDb |
| 66 | 1100.0 | 17/9, 32/17, 36/19 | M7 | major 7th | C# | M7, d8 | major 7th, dim 8ve | C#, Db | C#, Db |
| 67 | 1116.7 | 19/10, 21/11, 40/21 | ^M7 | upmajor 7th | ^C# | LM7, Kd8 | large major 7th, comma-wide dim 8ve | LC#, KDb | KC#, KDb |
| 68 | 1133.3 | 25/13, 27/14, 48/25, 52/27 | ^^M7 | dupmajor 7th | ^^C# | SM7, KKd8 | supermajor 7th, classic dim 8ve | SC#, KKDb | SC#, SDb, (KKDb) |
| 69 | 1150.0 | 35/18, 39/20, 64/33 | ^3M7, v38 | trupmajor 7th, trud octave | ^3C#, v3D | HM7, u8, h8 | hypermajor 7th, unter 8ve, hypo 8ve | HC#, uD, hD | UC#, uDb, uD |
| 70 | 1166.7 | 49/25, 55/28, 63/32, 88/45, 96/49 | vv8 | dud octave | vvD | s8, o8 | sub 8ve, off 8ve | sD, oD | sD |
| 71 | 1183.3 | 99/50, 160/81, 180/91, 196/99, 208/105 | v8 | down octave | vD | k8, l8 | comma-narrow 8ve, little 8ve | kD, lD | kD |
| 72 | 1200.0 | 2/1 | P8 | perfect octave | D | P8 | perfect octave | D | D |
- ↑ Based on treating 72edo as a 19-limit temperament; other approaches are also possible. For lower limits see Table of 72edo intervals.
Interval quality and chord names in color notation
Combining ups and downs notation with color notation, qualities can be loosely associated with colors:
| Quality | Color | Monzo format | Examples |
|---|---|---|---|
| dudminor | zo | (a b 0 1) | 7/6, 7/4 |
| minor | fourthward wa | (a b), b < -1 | 32/27, 16/9 |
| upminor | gu | (a b -1) | 6/5, 9/5 |
| dupminor, downmid |
luyo | (a b 1 0 -1) | 15/11 |
| tho | (a b 0 0 0 1) | 13/8, 13/9 | |
| mid | ilo | (a b 0 0 1) | 11/9, 11/6 |
| lu | (a b 0 0 -1) | 12/11, 18/11 | |
| upmid, dudmajor |
logu | (a b -1 0 1) | 11/10 |
| thu | (a b 0 0 0 -1) | 16/13, 18/13 | |
| downmajor | yo | (a b 1) | 5/4, 5/3 |
| major | fifthward wa | (a b), b > 1 | 9/8, 27/16 |
| dupmajor | ru | (a b 0 -1) | 9/7, 12/7 |
| trupmajor, trudminor |
thogu | (a b -1 0 0 1) | 13/10 |
| thuyo | (a b 1 0 0 -1) | 15/13 |
All 72edo chords can be named using ups and downs. An up, down or mid after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are. Here are the zo, gu, ilo, yo and ru triads:
| Color of the 3rd | JI chord | Notes as edosteps | Notes of C chord | Written name | Spoken name |
|---|---|---|---|---|---|
| zo | 6:7:9 | 0-16-42 | C vvEb G | Cvvm | C dudminor |
| gu | 10:12:15 | 0-19-42 | C ^Eb G | C^m | C upminor |
| ilo | 18:22:27 | 0-21-42 | C v3E G | C~ | C mid |
| yo | 4:5:6 | 0-23-42 | C vE G | Cv | C downmajor or C down |
| ru | 14:18:27 | 0-26-42 | C ^^E G | C^^ | C dupmajor or C dup |
For a more complete list, see Ups and Downs Notation #Chord names in other EDOs.
Relationship between primes and rings
In 72tet, there are 6 rings. 12edo is the plain ring; thus every 6 degrees is the 3-limit.
Then, after each subsequent degree in reverse, a new prime limit is unveiled from it:
- −1 degree (the down ring) corrects 81/64 to 5/4 via 80/81
- −2 degrees (the dud ring) corrects 16/9 to 7/4 via 63/64
- +3 degrees (the trup ring) corrects 4/3 to 11/8 via 33/32
- +2 degrees (the dup ring) corrects 128/81 to 13/8 via 1053/1024
- 0 degrees (the plain ring) corrects 256/243 to 17/16 via 4131/4096
- 0 degrees (the plain ring) corrects 32/27 to 19/16 via 513/512
Thus the product of a ratio's monzo with ⟨0 0 -1 -2 3 2 0 0], modulo 6, specifies which ring the ratio lies on.
Notations
Ups and downs notation
72edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Half-sharps and half-flats can be used to avoid triple arrows:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
Alternative ups and downs have sharps and flats with arrows borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
|
If double arrows are not desirable, arrows can be attached to quarter-tone accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
|
Sagittal notation
This notation uses the same sagittal sequence as EDOs 65-EDO and 79, and is a superset of the notations for EDOs 36, 24, 18, 12, 8, and 6.
Evo flavor

Revo flavor

Evo-SZ flavor

From the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 72edo in the Revo flavor of Sagittal:
Ivan Wyschnegradsky's notation
| Semitones | 0 | 1⁄6 | 1⁄3 | 1⁄2 | 2⁄3 | 5⁄6 | 1 | 1+1⁄6 | 1+1⁄3 | 1+1⁄2 | 1+2⁄3 | 1+5⁄6 | 2 | 2+1⁄6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
|
|
|
|
|
|
JI approximation

Interval mappings
The following table shows how 15-odd-limit intervals are represented in 72edo. Prime harmonics are in bold.
As 72edo is consistent in the 15-odd-limit, the mappings by direct approximation and through the patent val are identical.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 7/6, 12/7 | 0.204 | 1.2 |
| 11/6, 12/11 | 0.637 | 3.8 |
| 7/5, 10/7 | 0.821 | 4.9 |
| 11/7, 14/11 | 0.841 | 5.0 |
| 9/5, 10/9 | 0.930 | 5.6 |
| 5/3, 6/5 | 1.025 | 6.2 |
| 11/8, 16/11 | 1.318 | 7.9 |
| 11/10, 20/11 | 1.662 | 10.0 |
| 9/7, 14/9 | 1.751 | 10.5 |
| 3/2, 4/3 | 1.955 | 11.7 |
| 7/4, 8/7 | 2.159 | 13.0 |
| 15/13, 26/15 | 2.259 | 13.6 |
| 11/9, 18/11 | 2.592 | 15.6 |
| 15/14, 28/15 | 2.776 | 16.7 |
| 5/4, 8/5 | 2.980 | 17.9 |
| 13/9, 18/13 | 3.284 | 19.7 |
| 15/11, 22/15 | 3.617 | 21.7 |
| 9/8, 16/9 | 3.910 | 23.5 |
| 13/10, 20/13 | 4.214 | 25.3 |
| 15/8, 16/15 | 4.935 | 29.6 |
| 13/7, 14/13 | 5.035 | 30.2 |
| 13/12, 24/13 | 5.239 | 31.4 |
| 13/11, 22/13 | 5.876 | 35.3 |
| 13/8, 16/13 | 7.194 | 43.2 |
Zeta properties
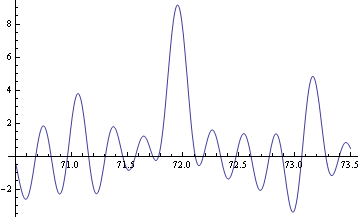
72edo is the ninth zeta integral edo, as well as being a peak and gap edo, and the maximum value of the Z function in the region near 72 occurs at 71.9506, giving an octave of 1200.824 cents, the stretched octaves of the zeta tuning. Below is a plot of Z in the region around 72.
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 380zpi | 71.950607 | 16.678108 | 9.157547 | 7.501282 | 1.625363 | 19.964746 | 1200.823788 | 0.823788 | 18 | 13 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3.5 | 15625/15552, 531441/524288 | [⟨72 114 167]] | +0.839 | 0.594 | 3.56 |
| 2.3.5.7 | 225/224, 1029/1024, 4375/4374 | [⟨72 114 167 202]] | +0.822 | 0.515 | 3.09 |
| 2.3.5.7.11 | 225/224, 243/242, 385/384, 4000/3993 | [⟨72 114 167 202 249]] | +0.734 | 0.493 | 2.96 |
| 2.3.5.7.11.13 | 169/168, 225/224, 243/242, 325/324, 385/384 | [⟨72 114 167 202 249 266]] | +0.936 | 0.638 | 3.82 |
| 2.3.5.7.11.13.17 | 169/168, 221/220, 225/224, 243/242, 273/272, 325/324 | [⟨72 114 167 202 249 266 294]] | +0.975 | 0.599 | 3.59 |
| 2.3.5.7.11.13.17.19 | 153/152, 169/168, 210/209, 221/220, 225/224, 243/242, 273/272 | [⟨72 114 167 202 249 266 294 306]] | +0.780 | 0.762 | 4.57 |
- 72et has lower relative errors than any previous equal temperaments in the 7-, 11-, 13-, 17-, and 19-limit. The next equal temperaments doing better in these subgroups are 99, 270, 224, 494, and 217, respectively.
Commas
Commas tempered out by 72edo include…
| Prime limit |
Ratio[note 1] | Monzo | Cents | Name(s) |
|---|---|---|---|---|
| 3 | (12 digits) | [-19 12⟩ | 23.46 | Pythagorean comma |
| 5 | 15625/15552 | [-6 -5 6⟩ | 8.11 | Kleisma |
| 5 | (16 digits) | [-25 7 6⟩ | 31.57 | Ampersand comma |
| 5 | (18 digits) | [-13 17 -6⟩ | 15.35 | Graviton |
| 5 | (26 digits) | [1 -27 18⟩ | 0.86 | Ennealimma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Marvel comma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.43 | Gamelisma |
| 7 | 2401/2400 | [-5 -1 -2 4⟩ | 0.72 | Breedsma |
| 7 | 4375/4374 | [-1 -7 4 1⟩ | 0.40 | Ragisma |
| 7 | 16875/16807 | [0 3 4 -5⟩ | 6.99 | Mirkwai comma |
| 7 | 19683/19600 | [-4 9 -2 -2⟩ | 7.32 | Cataharry comma |
| 7 | (12 digits) | [-6 -8 2 5⟩ | 1.12 | Wizma |
| 7 | (12 digits) | [-4 6 -6 3⟩ | 0.33 | Landscape comma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.14 | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.93 | Werckisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.21 | Swetisma |
| 11 | 1375/1372 | [-2 0 3 -3 1⟩ | 3.78 | Moctdel comma |
| 11 | 3025/3024 | [-4 -3 2 -1 2⟩ | 0.57 | Lehmerisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Wizardharry comma |
| 11 | 6250/6237 | [1 -4 5 -1 -1⟩ | 3.60 | Liganellus comma |
| 11 | 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Kalisma |
| 11 | (14 digits) | [16 -3 0 0 6⟩ | 2.04 | Nexus comma |
| 13 | 169/168 | [-3 -1 0 -1 0 2⟩ | 10.27 | Buzurgisma |
| 13 | 325/324 | [-2 -4 2 0 0 1⟩ | 5.34 | Marveltwin comma |
| 13 | 351/350 | [-1 3 -2 -1 0 1⟩ | 4.94 | Ratwolfsma |
| 13 | 364/363 | [2 -1 0 1 -2 1⟩ | 4.76 | Minor minthma |
| 13 | 625/624 | [-4 -1 4 0 0 -1⟩ | 2.77 | Tunbarsma |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.56 | Island comma |
| 13 | 729/728 | [-3 6 0 -1 0 -1⟩ | 2.38 | Squbema |
| 13 | 1001/1000 | [-3 0 -3 1 1 1⟩ | 1.73 | Sinbadma |
| 13 | 1575/1573 | [2 2 1 -2 -1⟩ | 2.20 | Nicola |
| 13 | 1716/1715 | [2 1 -1 -3 1 1⟩ | 1.01 | Lummic comma |
| 13 | 2080/2079 | [5 -3 1 -1 -1 1⟩ | 0.83 | Ibnsinma |
| 13 | 6656/6655 | [9 0 -1 0 -3 1⟩ | 0.26012 | Jacobin comma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Rank-2 temperaments
72edo provides the optimal patent val for miracle and wizard in the 7-limit, miracle, catakleismic, bikleismic, compton, ennealimnic, ennealiminal, enneaportent, marvolo and catalytic in the 11-limit, and catakleismic, bikleismic, compton, comptone, enneaportent, ennealim, catalytic, marvolo, manna, hendec, lizard, neominor, hours, and semimiracle in the 13-limit.
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 1\72 | 16.7 | 105/104 | Quincy |
| 1 | 5\72 | 83.3 | 21/20 | Marvolo |
| 1 | 7\72 | 116.7 | 15/14 | Miracle / benediction / manna |
| 1 | 17\72 | 283.3 | 13/11 | Neominor |
| 1 | 19\72 | 316.7 | 6/5 | Catakleismic |
| 1 | 25\72 | 416.7 | 14/11 | Sqrtphi |
| 1 | 29\72 | 483.3 | 45/34 | Hemiseven |
| 1 | 31\72 | 516.7 | 27/20 | Marvo / zarvo |
| 1 | 35\72 | 583.3 | 7/5 | Cotritone |
| 2 | 5\72 | 83.3 | 21/20 | Harry |
| 2 | 7\72 | 116.7 | 15/14 | Semimiracle |
| 2 | 11\72 | 183.3 | 10/9 | Unidec / hendec |
| 2 | 21\72 (19\72) |
316.7 (283.3) |
6/5 (13/11) |
Bikleismic |
| 2 | 23\72 (13\72) |
383.3 (216.7) |
5/4 (17/15) |
Wizard / lizard / gizzard |
| 3 | 11\72 | 183.3 | 10/9 | Mirkat |
| 3 | 19\72 (5\72) |
316.7 (83.3) |
6/5 (21/20) |
Tritikleismic |
| 4 | 19\72 (1\72) |
316.7 (16.7) |
6/5 (105/104) |
Quadritikleismic |
| 8 | 34\72 (2\72) |
566.7 (33.3) |
168/121 (55/54) |
Octowerck / octowerckis |
| 8 | 35\72 (1\72) |
583.3 (16.7) |
7/5 (100/99) |
Octoid / octopus |
| 9 | 19\72 (3\72) |
316.7 (50.0) |
6/5 (36/35) |
Ennealimmal / ennealimnic |
| 9 | 23\72 (1\72) |
383.3 (16.7) |
5/4 (105/104) |
Enneaportent |
| 12 | 23\72 (1\72) |
383.3 (16.7) |
5/4 (100/99) |
Compton / comptone |
| 18 | 19\72 (1\72) |
316.7 (16.7) |
6/5 (105/104) |
Hemiennealimmal |
| 24 | 23\72 (1\72) |
383.3 (16.7) |
5/4 (105/104) |
Hours |
| 36 | 23\72 (1\72) |
383.3 (16.7) |
5/4 (81/80) |
Gamelstearn |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Scales
- Smithgw72a, smithgw72b, smithgw72c, smithgw72d, smithgw72e, smithgw72f, smithgw72g, smithgw72h, smithgw72i, smithgw72j
- Blackjack, miracle_8, miracle_10, miracle_12, miracle_12a, miracle_24hi, miracle_24lo
- Keenanmarvel, xenakis_chrome, xenakis_diat, xenakis_schrome
- Euler(24255) genus in 72 equal
- JuneGloom
- Harry Partch's 43-tone scale: 1 2 2 2 2 1 1 1 2 2 2 1 2 2 2 1 2 2 1 2 2 2 2 2 1 2 2 1 2 2 2 1 2 2 2 1 1 1 2 2 2 2 1
- Magnetosphere, Blackened skies, Lost spirit
- 5- to 10-tone scales in 72edo
Harmonic scale
Mode 8 of the harmonic series—harmonics 8 through 16, octave repeating—is well-represented in 72edo. Note that all the different step sizes are distinguished, except for 13:12 and 14:13 (conflated to 8\72edo, 133.3 cents) and 15:14 and 16:15 (conflated to 7\72edo, 116.7 cents, the generator for miracle temperament).
| Harmonics in "Mode 8": | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| …as JI Ratio from 1/1: | 1/1 | 9/8 | 5/4 | 11/8 | 3/2 | 13/8 | 7/4 | 15/8 | 2/1 | ||||||||
| …in cents: | 0 | 203.9 | 386.3 | 551.3 | 702.0 | 840.5 | 968.8 | 1088.3 | 1200.0 | ||||||||
| Nearest degree of 72edo: | 0 | 12 | 23 | 33 | 42 | 50 | 58 | 65 | 72 | ||||||||
| …in cents: | 0 | 200.0 | 383.3 | 550.0 | 700.0 | 833.3 | 966.7 | 1083.3 | 1200.0 | ||||||||
| Steps as Freq. Ratio: | 9:8 | 10:9 | 11:10 | 12:11 | 13:12 | 14:13 | 15:14 | 16:15 | |||||||||
| …in cents: | 203.9 | 182.4 | 165.0 | 150.6 | 138.6 | 128.3 | 119.4 | 111.7 | |||||||||
| Nearest degree of 72edo: | 12 | 11 | 10 | 9 | 8 | 8 | 7 | 7 | |||||||||
| …in cents: | 200.0 | 183.3 | 166.7 | 150.0 | 133.3 | 133.3 | 116.7 | 116.7 |
Instruments
If one can get six 12edo instruments tuned a twelfth-tone apart, it is possible to use these instruments in combination to play the full gamut of 72edo (see Music).
One can also use a skip fretting system:
Alternatively, an appropriately mapped keyboard of sufficient size is usable for playing 72edo:
Music
- Goetic Synchronities (2023)
- Rainy Day Generative Pillow (2024)
- Lazy Sunday[dead link] in the lazysunday scale
- Blumenstück (2000)
- in vain (2000) (score)
- Twinkle canon – 72 edo[dead link]
- The Miracle Canon, 3-in-1 on a Ground
- Sicilienne in Miracle
- Arietta with 5 Variations, for Organ (2024)
- Χenomorphic Ghost Storm (2022)
External links
- OrthodoxWiki Article on Byzantine chant, which uses 72edo
- Ekmelic Music Society/Gesellschaft für Ekmelische Musik, a group of composers and researchers dedicated to 72edo music
- Rick Tagawa's 72edo site, including theory and composers' list
- Danny Wier, composer and musician who specializes in 72-edo
- 72-ed2 / 72-edo / 72-ET / 72-tone equal-temperament on Tonalsoft Encyclopedia