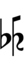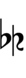65edo

← 64edo

65edo

66edo →

Prime factorization	5 × 13
Step size	18.4615 ¢
Fifth	38\65 (701.538 ¢)
Semitones (A1:m2)	6:5 (110.8 ¢ : 92.31 ¢)
Consistency limit	5
Distinct consistency limit	5

65 equal divisions of the octave (abbreviated 65edo or 65ed2), also called 65-tone equal temperament (65tet) or 65 equal temperament (65et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 65 equal parts of about 18.5 ¢ each. Each step represents a frequency ratio of 2^1/65, or the 65th root of 2.

Theory

65et can be characterized as the temperament which tempers out 32805/32768 (schisma), 78732/78125 (sensipent comma), 393216/390625 (würschmidt comma), and [-13 17 -6⟩ (graviton). In the 7-limit, there are two different maps; the first is ⟨65 103 151 182] (65), tempering out 126/125, 245/243 and 686/675, so that it supports sensi, and the second is ⟨65 103 151 183] (65d), tempering out 225/224, 3125/3087, 4000/3969 and 5120/5103, so that it supports garibaldi. In both cases, the tuning privileges the 5-limit over the 7-limit, as the 5-limit of 65 is quite accurate. The same can be said for the two different versions of 7-limit würschmidt temperament (wurschmidt and worschmidt) these two mappings provide.

65edo approximates the intervals 3/2, 5/4, 11/8, 19/16, 23/16, 31/16 and 47/32 well, so that it does a good job representing the 2.3.5.11.19.23.31.47 just intonation subgroup. To this one may want to add 17/16, 29/16 and 43/32, giving the 47-limit no-7's no-13's no-37's no-41's subgroup 2.3.5.11.17.19.23.29.31.43.47. In this sense it is a tuning of schismic/nestoria that focuses on the very primes that 53edo neglects (which instead elegantly connects primes 7, 13, 37, and 41 to nestoria). Also of interest is the 19-limit 2*65 subgroup 2.3.5.49.11.91.119.19, on which 65 has the same tuning and commas as the zeta edo 130edo.

Prime harmonics

Approximation of prime harmonics in 65edo

Harmonic		2	3	5	7	11	13	17	19	23	29	31	37	41	43	47
Error	Absolute (¢)	+0.00	-0.42	+1.38	-8.83	+2.53	+8.70	+5.81	-2.13	-0.58	+4.27	-0.42	+7.12	-4.45	+5.41	-0.89
	Relative (%)	+0.0	-2.3	+7.5	-47.8	+13.7	+47.1	+31.5	-11.5	-3.2	+23.1	-2.3	+38.6	-24.1	+29.3	-4.8
Steps (reduced)		65 (0)	103 (38)	151 (21)	182 (52)	225 (30)	241 (46)	266 (6)	276 (16)	294 (34)	316 (56)	322 (62)	339 (14)	348 (23)	353 (28)	361 (36)

Subsets and supersets

65edo contains 5edo and 13edo as subsets. The offset between a just perfect fifth at 702 cents and the 13edo superfifth at 738.5 cents, is approximately 2 degrees of 65edo. Therefore, an instrument fretted to 13edo, with open strings tuned to 3-limit intervals such as 4/3, 3/2, 9/8, 16/9 etc, will approximate a subset of 65edo. For an example of this, see Andrew Heathwaite's composition Rubble: a Xenuke Unfolded.

130edo, which doubles its, corrects its approximation to harmonics 7 and 13.

Intervals

#	Cents	Approximate ratios	Ups and downs notation
0	0.00	1/1	P1	D
1	18.46	81/80, 88/87, 93/92, 94/93, 95/94, 96/95, 100/99, 121/120, 115/114, 116/115, 125/124	^1	^D
2	36.92	45/44, 46/45, 47/46, 48/47, 55/54, 128/125	^^1	^^D
3	55.38	30/29, 31/30, 32/31, 33/32, 34/33	vvm2	vvEb
4	73.85	23/22, 24/23, 25/24, 47/45	vm2	vEb
5	92.31	18/17, 19/18, 20/19, 58/55, 135/128, 256/243	m2	Eb
6	110.77	16/15, 17/16, 33/31	A1/^m2	D#/^Eb
7	129.23	14/13, 27/25, 55/51	v~2	^^Eb
8	147.69	12/11, 25/23	~2	vvvE
9	166.15	11/10, 32/29	^~2	vvE
10	184.62	10/9, 19/17	vM2	vE
11	203.08	9/8, 64/57	M2	E
12	221.54	17/15, 25/22, 33/29, 58/51	^M2	^E
13	240.00	23/20, 31/27, 38/33, 54/47, 55/48	^^M2	^^E
14	258.46	22/19, 29/25, 36/31, 64/55	vvm3	vvF
15	276.92	20/17, 27/23, 34/29, 75/64	vm3	vF
16	295.38	19/16, 32/27	m3	F
17	313.85	6/5, 55/46	^m3	^F
18	332.31	23/19, 40/33	v~3	^^F
19	350.77	11/9, 27/22, 38/31	~3	^^^F
20	369.23	26/21, 47/38, 68/55	^~3	vvF#
21	387.69	5/4, 64/51	vM3	vF#
22	406.15	19/15, 24/19, 29/23, 34/27, 81/64	M3	F#
23	424.62	23/18, 32/25	^M3	^F#
24	443.08	22/17, 31/24, 40/31, 128/99	^^M3	^^F#
25	461.54	30/23, 47/36, 72/55	vv4	vvG
26	480.00	29/22, 33/25, 62/47	v4	vG
27	498.46	4/3	P4	G
28	516.92	23/17, 27/20, 31/23	^4	^G
29	535.38	15/11, 34/25, 64/47	v~4	^^G
30	553.85	11/8, 40/29, 62/45	~4	^^^G
31	572.31	25/18, 32/23	^~4/vd5	vvG#/vAb
32	590.77	24/17, 31/22, 38/27, 45/32	vA4/d5	vG#/Ab
33	609.23	17/12, 27/19, 44/31, 64/45	A4/^d5	G#/^Ab
34	627.69	36/25, 23/16	^A4/v~5	^G#/^^Ab
35	646.15	16/11, 29/20, 45/31	~5	vvvA
36	664.62	22/15, 25/17, 47/32	^~5	vvA
37	683.08	34/23, 40/27, 46/31	v5	vA
38	701.54	3/2	P5	A
39	720.00	44/29, 50/33, 47/31	^5	^A
40	738.46	23/15, 55/36, 72/47	^^5	^^A
41	756.92	17/11, 48/31, 31/20, 99/64	vvm6	vvBb
42	775.38	25/16, 36/23	vm6	vBb
43	793.85	19/12, 27/17, 30/19, 46/29, 128/81	m6	Bb
44	812.31	8/5, 51/32	^m6	^Bb
45	830.77	21/13, 55/34, 76/47	v~6	^^Bb
46	849.23	18/11, 31/19, 44/27	~6	vvvB
47	867.69	33/20, 38/23	^~6	vvB
48	886.15	5/3, 92/55	vM6	vB
49	904.62	27/16, 32/19	M6	B
50	923.08	17/10, 29/17, 46/27, 128/75	^M6	^B
51	941.54	19/11, 31/18, 50/29, 55/32	^^M6	^^B
52	960.00	33/19, 40/23, 47/27, 54/31, 96/55	vvm7	vvC
53	978.46	30/17, 44/25, 51/29, 58/33	vm7	vC
54	996.92	16/9, 57/32	m7	C
55	1015.38	9/5, 34/19	^m7	^C
56	1033.85	20/11, 29/16	v~7	^^C
57	1052.31	11/6, 46/25	~7	^^^C
58	1070.77	13/7, 50/27, 102/55	^~7	vvC#
59	1089.23	15/8, 32/17, 62/33	vM7	vC#
60	1107.69	17/9, 19/10, 36/19, 55/29, 243/128, 256/135	M7	C#
61	1126.15	23/12, 44/23, 48/25, 90/47	^M7	^C#
62	1144.62	29/15, 31/16, 33/17, 60/31, 64/33	^^M7	^^C#
63	1163.08	45/23, 47/24, 88/45, 92/47, 108/55, 125/64	vv8	vvD
64	1181.54	87/55, 93/47, 95/48, 99/50, 115/58, 160/81, 184/93, 188/95, 228/115, 240/121, 248/125	v8	vD
65	1200.00	2/1	P8	D

Notation

Ups and downs notation

65edo can be notated with ups and downs, spoken as up, dup, trup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, trud, dupflat etc.

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12
Sharp symbol
Flat symbol

Half-sharps and half-flats can be used to avoid triple arrows:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12
Sharp symbol
Flat symbol

Alternative ups and downs have arrows borrowed from extended Helmholtz–Ellis notation:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Sharp symbol
Flat symbol

If double arrows are not desirable, arrows can be attached to quarter-tone accidentals:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Sharp symbol
Flat symbol

Ivan Wyschnegradsky's notation

Since a sharp raises by six steps, Wyschnegradsky accidentals borrowed from 72edo can also be used:

Step offset	0	1	2	3	4	5	6	7	8	9	10	11	12	13
Sharp symbol
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as EDOs 72 and 79.

Evo flavor

Revo flavor

Evo-SZ flavor

Approximation to JI

Zeta peak index

Tuning			Strength				Octave (cents)		Integer limit
ZPI	Steps per 8ve	Step size (cents)	Height		Integral	Gap	Size	Stretch	Consistent	Distinct
			Tempered	Pure
334zpi	65.015845	18.457039	7.813349	7.642373	1.269821	16.514861	1199.707547	−0.292453	6	6

Regular temperament properties

Subgroup	Comma list	Mapping	Optimal 8ve stretch (¢)	Tuning error
				Absolute (¢)	Relative (%)
2.3	[-103 65⟩	[⟨65 103]]	+0.131	0.131	0.71
2.3.5	32805/32768, 78732/78125	[⟨65 103 151]]	−0.110	0.358	1.94
2.3.5.11	243/242, 4000/3993, 5632/5625	[⟨65 103 151 225]]	−0.266	0.410	2.22

Rank-2 temperaments

Table of rank-2 temperaments by generator

Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperament
1	3\65	55.38	33/32	Escapade
1	9\65	166.15	11/10	Squirrel etc.
1	12\65	221.54	25/22	Hemisensi
1	19\65	350.77	11/9	Karadeniz
1	21\65	387.69	5/4	Würschmidt
1	24\65	443.08	162/125	Sensipent
1	27\65	498.46	4/3	Helmholtz / nestoria / photia
1	28\65	516.92	27/20	Larry
5	20\65 (6\65)	369.23 (110.77)	99/80 (16/15)	Quintosec
5	27\65 (1\65)	498.46 (18.46)	4/3 (81/80)	Quintile
5	30\65 (4\65)	553.85 (73.85)	11/8 (25/24)	Countdown

* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct

Scales

• Amulet^{[idiosyncratic term]}, (approximated from 25edo, subset of würschmidt): 5 3 5 5 3 5 12 5 5 3 5 12 5
• Photia7
• Photia12
• Skateboard7

Instruments

Lumatone mapping for 65edo