Garibaldi
Garibaldi is a 7-limit (and higher) temperament of the schismatic family. It is an extension of helmholtz temperament beyond the 5-limit but with the same simple chain-of-fifths structure (so that standard notation may be used). The garibaldi temperament tempers together the Pythagorean, syntonic, and archytas commas into a singular generalized "comma", which can be used to reach intervals of 3, 5, and 7. As in helmholtz temperament, 5/4 is mapped to the diminished fourth (e.g. C–F♭; a comma-flat major third), and the new mapping specific to garibaldi is that 7/4 is mapped to the double-diminished octave (e.g. C–C𝄫; a comma-flat minor seventh). This makes garibaldi a marvel temperament and a hemifamity temperament. Tuning the fifth a fraction of a cent sharp gives the best tunings.
Immediate 11-limit extensions include cassandra (41 & 53), mapping 11/8 to +23 fifths, andromeda (29 & 41), mapping 11/8 to −18 fifths, and helenus (53 & 65d), mapping 11/8 to −30 fifths. Garibaldi is most naturally a 2.3.5.7.19-subgroup temperament due to its immediate availability of 19/16 at the minor third (C–E♭). This is sometimes known as garibaldi nestoria.
Garibaldi was named in honor of Eduardo Sábat-Garibaldi, who developed the dinarra, a 53-tone microtonal guitar in the 1/9-schisma tuning.
See Schismatic family #Garibaldi for technical data.
Interval chain
In the following table, odd harmonics 1–21 and their inverses are in bold.
| # | Cents* | Approximate ratios | |||
|---|---|---|---|---|---|
| 2.3.5.7.19 subgroup | 13-limit extensions | ||||
| Cassandra | Andromeda | Helenus | |||
| 0 | 0.00 | 1/1 | |||
| 1 | 702.10 | 3/2 | |||
| 2 | 204.20 | 9/8 | |||
| 3 | 906.30 | 27/16, 32/19, 42/25 | 22/13 | 22/13 | 22/13 |
| 4 | 408.40 | 19/15, 24/19 | 14/11 | ||
| 5 | 1110.50 | 19/10, 36/19, 40/21 | 21/11 | ||
| 6 | 612.60 | 10/7 | |||
| 7 | 114.70 | 15/14, 16/15 | 14/13 | ||
| 8 | 816.80 | 8/5 | 21/13 | ||
| 9 | 318.90 | 6/5 | 40/33 | ||
| 10 | 1021.00 | 9/5, 38/21 | 20/11 | ||
| 11 | 523.09 | 19/14, 27/20 | 15/11 | ||
| 12 | 25.19 | 50/49, 57/56, 64/63, 81/80 | 40/39, 45/44 | ||
| 13 | 727.29 | 32/21 | 20/13 | ||
| 14 | 229.39 | 8/7 | 15/13 | ||
| 15 | 931.49 | 12/7 | 19/11 | ||
| 16 | 433.59 | 9/7 | 14/11 | ||
| 17 | 1135.69 | 27/14, 48/25 | 52/27 | 64/33 | 21/11 |
| 18 | 637.79 | 36/25, 81/56 | 13/9 | 16/11, 19/13 | |
| 19 | 139.89 | 27/25 | 13/12 | 12/11 | 14/13 |
| 20 | 841.99 | 57/35, 80/49 | 13/8, 44/27 | 18/11, 64/39 | 21/13 |
| 21 | 344.09 | 60/49 | 11/9, 39/32 | 16/13, 27/22 | 40/33 |
| 22 | 1046.19 | 64/35 | 11/6 | 24/13 | 20/11 |
| 23 | 548.29 | 48/35 | 11/8, 26/19 | 18/13 | 15/11 |
| 24 | 50.39 | 36/35 | 33/32 | 27/26 | 40/39, 45/44 |
| 25 | 752.49 | 54/35 | 20/13 | ||
| 26 | 254.59 | 57/49, 81/70, 144/125 | 22/19 | 15/13 | |
| 27 | 956.69 | 171/98, 216/125, 256/147 | 26/15 | 19/11 | |
| 28 | 458.79 | 64/49 | 13/10 | ||
| 29 | 1160.89 | 96/49 | 39/20, 88/45 | 64/33 | |
| 30 | 662.99 | 72/49 | 22/15 | 16/11, 19/13 | |
| 31 | 165.08 | 54/49 | 11/10 | 12/11 | |
| 32 | 867.18 | 81/49 | 33/20 | 18/11, 64/39 | |
| 33 | 369.28 | 216/175 | 26/21 | 16/13, 27/22 | |
| 34 | 1071.38 | 324/175 | 13/7 | 24/13 | |
| 35 | 573.48 | 243/175 | 18/13 | ||
| 36 | 75.58 | 256/245 | 22/21 | 27/26 | |
| 37 | 777.68 | 384/245 | 11/7 | ||
| 38 | 279.78 | 288/245 | |||
| 39 | 981.88 | 432/245 | |||
| 40 | 483.98 | 324/245 | |||
| 41 | 1186.08 | 486/245 | |||
* In 2.3.5.7.19-subgroup CWE tuning
As a detemperament of 12et
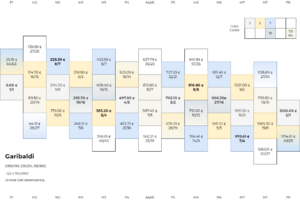
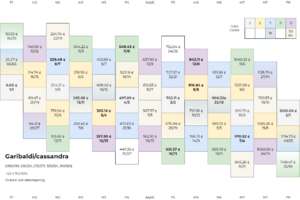
Garibaldi is very naturally considered as a detemperament of the 12 equal temperament. The table below shows a 53-tone detempered scale, with a generator range of -26 to +26. Each interval category of the 12 equal temperament is further divided into "double-sub", "sub", "plain", "super" and "double-super" qualities, separated by an enharmonic diesis, which represents the syntonic~septimal comma; the "plain" type here consists of a 5L 7s scale in 6|5 mode. Combining this division with the minor and major qualities of the 12 equal temperament, and calling the "double-sub major" and "double-super minor" qualities artoneutral and tendoneutral, respectively, garibaldi gives us at least eight qualities for each diatonic category: subminor, minor, supraminor, artoneutral, tendoneutral, submajor, major, and supermajor.
Notice also the little comma between artoneutral and tendoneutral. This interval spans 41 generator steps. 41edo tempers it out so that it merges artoneutral and tendoneutral into one neutral interval whereas 53edo exaggerates it to the size of the syntonic~septimal comma. 94edo tunes it to one half the size of the syntonic~septimal comma, which can be seen as a good compromise.
| # | Interval category |
"Double-Sub" | "Sub" | "Plain" | "Super" | "Double-super" | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gen. | Cents* | Ratios | Gen. | Cents* | Ratios | Gen. | Cents* | Ratios | Gen. | Cents* | Ratios | Gen. | Cents* | Ratios | ||
| 0 | P1 | 0 | 0.0 | 1/1 | 12 | 25.2 | 64/63~81/80 | 24 | 50.5 | 33/32~36/35 | ||||||
| 1 | m2 | −17 | 64.2 | 27/26~28/27 | −5 | 89.5 | 20/19~21/20 | 7 | 114.7 | 15/14~16/15 | 19 | 140.0 | 13/12 | |||
| 2 | M2 | −22 | 153.7 | 12/11 | −10 | 178.9 | 10/9 | 2 | 204.2 | 9/8 | 14 | 229.5 | 8/7 | 26 | 254.7 | 22/19 |
| 3 | m3 | −15 | 268.4 | 7/6 | −3 | 293.6 | 13/11~19/16 | 9 | 318.9 | 6/5 | 21 | 344.2 | 11/9 | |||
| 4 | M3 | −20 | 357.9 | 16/13 | −8 | 383.2 | 5/4 | 4 | 408.4 | 19/15~24/19 | 16 | 433.7 | 9/7 | |||
| 5 | P4 | −25 | 447.4 | 35/27 | −13 | 472.6 | 21/16 | −1 | 497.9 | 4/3 | 11 | 523.2 | 19/14 | 23 | 548.4 | 11/8 |
| 6 | A4, d5 | −18 | 562.1 | 18/13 | −6 | 587.4 | 7/5 | 6 | 612.6 | 10/7 | 18 | 637.9 | 13/9 | |||
| 7 | P5 | −23 | 651.6 | 16/11 | −11 | 676.8 | 28/19 | 1 | 702.1 | 3/2 | 13 | 727.4 | 32/21 | 25 | 752.6 | 54/35 |
| 8 | m6 | −16 | 766.3 | 14/9 | −4 | 791.6 | 19/12~30/19 | 8 | 816.8 | 8/5 | 20 | 842.1 | 13/8 | |||
| 9 | M6 | −21 | 855.8 | 18/11 | −9 | 881.1 | 5/3 | 3 | 906.3 | 22/13~27/16 | 15 | 931.6 | 12/7 | |||
| 10 | m7 | −26 | 945.3 | 19/11 | −14 | 970.5 | 7/4 | −2 | 995.8 | 16/9 | 10 | 1021.1 | 9/5 | 22 | 1046.3 | 11/6 |
| 11 | M7 | −19 | 1060.0 | 24/13 | −7 | 1085.3 | 15/8~28/15 | 5 | 1110.5 | 19/10~40/21 | 17 | 1135.8 | 27/14~52/27 | |||
| 12 | P8 | −24 | 1149.5 | 35/18~64/33 | −12 | 1174.7 | 63/32~65/33 | 0 | 1200.0 | 2/1 | ||||||
See the diagrams on the right for isomorphic versions.
Notation
Using schismic can be a challenge because it defies the tradition of tertian harmony in chain-of-fifths notation. The just major triad on C is C–Fb–G, for example. Due to the generalized comma of garibaldi, a natural choice is to adopt an additional module of accidentals such as arrows to represent the comma step, allowing them to write the chord above as C–vE–G.
| Ratio | Nominal | Example |
|---|---|---|
| 3/2 | Perfect fifth | C–G |
| 5/4 | Downmajor third | C–vE |
| 7/4 | Downminor seventh | C–vBb |
| 11/8 | Double-up fourth | C–^^F |
| 13/8 | Double-up minor sixth | C–^^Ab |
| 19/16 | Minor third | C–Eb |
| Ratio | Nominal | Example |
|---|---|---|
| 11/8 | Down-diminished fifth Double-down augmented fourth |
C–vGb C–vvF# |
| 13/8 | Double downmajor sixth | C–vvA |
| Ratio | Nominal | Example |
|---|---|---|
| 11/8 | Double-down diminished fifth Triple-down augmented fourth |
C–vvGb C–v3F# |
| 13/8 | Triple-down major sixth | C–v3A |
Chords and harmony
Traditional tertian harmony is effective. The default triads on the Pythagorean spine are undevicesimal in quality:
- 1–19/15–3/2 (C–E–G)
- 1–19/16–3/2 (C–Eb–G)
Note that the major third also represents 24/19, and the minor third, 13/11. These chords are typically associated with a sort of coldness and metalness, like those in 12edo if not more so.
If a warm, sweet, laid-back sound is desired, the thirds can be inflected inwards by a comma to yield
- 1–5/4–3/2 (C–vE–G)
- 1–6/5–3/2 (C–^Eb–G)
Contrarily, for a more sour and active sound, they can be inflected outwards by a comma to yield
- 1–9/7–3/2 (C–^E-G)
- 1–7/6–3/2 (C–vEb-G)
Scales
- Garibaldi5 – proper 2L 3s
- Garibaldi7 – improper 5L 2s
- Garibaldi12 – proper 5L 7s
- Garibaldi17 – improper 12L 5s
- Garibaldi24opt – optimized 24-note scale for 13-limit
Tunings
Target tunings
| Target | Minimax | Least squares | ||
|---|---|---|---|---|
| Generator | Eigenmonzo* | Generator | Eigenmonzo* | |
| 7-odd-limit | ~3/2 = 702.2086 ¢ | 7/6 | ~3/2 = 702.140 ¢ | [0 -25 11 35⟩ |
| 9-odd-limit | ~3/2 = 702.1928 ¢ | 9/7 | ~3/2 = 702.114 ¢ | [0 -27 7 17⟩ |
| Target | Minimax | Least squares | ||
|---|---|---|---|---|
| Generator | Eigenmonzo* | Generator | Eigenmonzo* | |
| 11-odd-limit | ~3/2 = 702.1928 ¢ | 9/7 | ~3/2 = 702.183 ¢ | [0 17 -52 -88 134⟩ |
| 13-odd-limit | ~3/2 = 702.1089 ¢ | 13/7 | ~3/2 = 702.128 ¢ | [0 -38 -80 -122 137 116⟩ |
| 15-odd-limit | ~3/2 = 702.1089 ¢ | 13/7 | ~3/2 = 702.112 ¢ | [0 -95 -137 -129 167 143⟩ |
| Target | Minimax | |
|---|---|---|
| Generator | Eigenmonzo* | |
| 11-odd-limit | ~3/2 = 702.6296 ¢ | 11/9 |
| 13-odd-limit | ~3/2 = 702.7558 ¢ | 13/9 |
| 15-odd-limit | ~3/2 = 702.7558 ¢ | 13/9 |
| Target | Minimax | |
|---|---|---|
| Generator | Eigenmonzo* | |
| 11-odd-limit | ~3/2 = 701.6435 ¢ | 11/9 |
| 13-odd-limit | ~3/2 = 701.6435 ¢ | 11/9 |
| 15-odd-limit | ~3/2 = 701.6435 ¢ | 11/9 |
Tuning spectra
Garibaldi
| Edo generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 7\12 | 700.0000 | Lower bound of 9-odd-limit, 2.3.5.7.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 19/16 | 700.8290 | 1/3 undevicesimal schisma | |
| 19/12 | 701.1105 | 1/4 undevicesimal schisma | |
| 38\65 | 701.5385 | 65d val | |
| 15/8 | 701.6759 | 1/7 schisma | |
| 5/4 | 701.7108 | 1/8 schisma | |
| 25/24 | 701.7252 | 2/17 schisma | |
| 5/3 | 701.7379 | 5-odd-limit minimax, 1/9 schisma | |
| 9/5 | 701.7596 | 1/10 schisma | |
| 81/80 | 701.7922 | 1/12 schisma | |
| 31\53 | 701.8868 | ||
| 3/2 | 701.9550 | Pythagorean tuning | |
| 36/35 | 702.0321 | ||
| 55\94 | 702.1277 | ||
| 9/7 | 702.1928 | 9-odd-limit minimax, 1/16 septimal schisma | |
| 7/6 | 702.2086 | 7-odd-limit minimax, 1/15 septimal schisma | |
| 49/48 | 702.2174 | 2/29 septimal schisma | |
| 7/4 | 702.2267 | 1/14 septimal schisma | |
| 19/10 | 702.2399 | ||
| 21/16 | 702.2476 | 1/13 septimal schisma | |
| 64/63 | 702.2720 | 1/12 septimal schisma | |
| 19/15 | 702.3111 | ||
| 24\41 | 702.4390 | ||
| 19/14 | 702.6079 | ||
| 21/19 | 702.6732 | ||
| 15/14 | 702.7775 | ||
| 7/5 | 702.9146 | ||
| 21/20 | 703.1066 | ||
| 17\29 | 703.4483 | Upper bound of 9-odd-limit, 2.3.5.7.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 13/11 | 703.5968 |
Cassandra
| Edo generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 7\12 | 700.0000 | Lower bound of 9-odd-limit diamond monotone | |
| 19/16 | 700.8290 | 1/3 undevicesimal schisma | |
| 19/12 | 701.1105 | 1/4 undevicesimal schisma | |
| 38\65 | 701.5385 | 65def val | |
| 15/8 | 701.6759 | 1/7 schisma | |
| 5/4 | 701.7108 | 1/8 schisma | |
| 25/24 | 701.7252 | 2/17 schisma | |
| 5/3 | 701.7379 | 5-odd-limit minimax, 1/9 schisma | |
| 9/5 | 701.7596 | 1/10 schisma | |
| 81/80 | 701.7922 | 1/12 schisma | |
| 19/13 | 701.8702 | ||
| 31\53 | 701.8868 | Lower bound of 11-, 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 15/13 | 701.9355 | ||
| 13/10 | 701.9362 | ||
| 3/2 | 701.9550 | Pythagorean tuning | |
| 13/8 | 702.0264 | ||
| 13/12 | 702.0301 | ||
| 36/35 | 702.0321 | ||
| 13/9 | 702.0343 | ||
| 19/11 | 702.0694 | ||
| 11/10 | 702.0969 | ||
| 15/11 | 702.1016 | ||
| 13/7 | 702.1089 | 13- and 15-odd-limit minimax | |
| 21/13 | 702.1135 | ||
| 55\94 | 702.1277 | ||
| 9/7 | 702.1928 | 9- and 11-odd-limit minimax, 1/16 septimal schisma | |
| 7/6 | 702.2086 | 7-odd-limit minimax, 1/15 septimal schisma | |
| 49/48 | 702.2174 | 2/29 septimal schisma | |
| 7/4 | 702.2267 | 1/14 septimal schisma | |
| 11/7 | 702.2295 | ||
| 11/8 | 702.2312 | ||
| 21/11 | 702.2371 | ||
| 19/10 | 702.2399 | ||
| 11/6 | 702.2438 | ||
| 21/16 | 702.2476 | 1/13 septimal schisma | |
| 11/9 | 702.2575 | ||
| 64/63 | 702.2720 | 1/12 septimal schisma | |
| 19/15 | 702.3111 | ||
| 24\41 | 702.4390 | Upper bound of 11-, 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 19/14 | 702.6079 | ||
| 21/19 | 702.6732 | ||
| 15/14 | 702.7775 | ||
| 7/5 | 702.9146 | ||
| 21/20 | 703.1066 | ||
| 17\29 | 703.4483 | 29ef val, upper bound of 9-odd-limit diamond monotone | |
| 13/11 | 703.5968 |
Andromeda
| Edo generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 7\12 | 700.0000 | Lower bound of 9- and 11-odd-limit diamond monotone | |
| 19/16 | 700.8290 | 1/3 undevicesimal schisma | |
| 19/12 | 701.1105 | 1/4 undevicesimal schisma | |
| 38\65 | 701.5385 | 65deeff val | |
| 15/8 | 701.6759 | 1/7 schisma | |
| 5/4 | 701.7108 | 1/8 schisma | |
| 25/24 | 701.7252 | 2/17 schisma | |
| 5/3 | 701.7379 | 5-odd-limit minimax, 1/9 schisma | |
| 9/5 | 701.7596 | 1/10 schisma | |
| 81/80 | 701.7922 | 1/12 schisma | |
| 31\53 | 701.8868 | 53ef val | |
| 3/2 | 701.9550 | Pythagorean tuning | |
| 36/35 | 702.0321 | ||
| 9/7 | 702.1928 | 9-odd-limit minimax, 1/16 septimal schisma | |
| 7/6 | 702.2086 | 7-odd-limit minimax, 1/15 septimal schisma | |
| 49/48 | 702.2174 | 2/29 septimal schisma | |
| 7/4 | 702.2267 | 1/14 septimal schisma | |
| 21/16 | 702.2476 | 1/13 septimal schisma | |
| 64/63 | 702.2720 | 1/12 septimal schisma | |
| 19/15 | 702.3111 | ||
| 24\41 | 702.4390 | Lower bound of 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 19/14 | 702.6079 | ||
| 11/9 | 702.6296 | 11-odd-limit minimax | |
| 11/6 | 702.6651 | ||
| 21/19 | 702.6732 | ||
| 11/8 | 702.7046 | ||
| 13/9 | 702.7558 | 13- and 15-odd-limit minimax | |
| 15/14 | 702.7775 | ||
| 13/12 | 702.7922 | ||
| 13/8 | 702.8320 | ||
| 7/5 | 702.9146 | ||
| 19/11 | 703.0797 | ||
| 21/20 | 703.1066 | ||
| 19/13 | 703.1659 | ||
| 15/11 | 703.3592 | ||
| 15/13 | 703.4101 | ||
| 17\29 | 703.4483 | Upper bound of 9-, 11-, 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 11/10 | 703.4996 | ||
| 13/10 | 703.5220 | ||
| 13/11 | 703.5968 | ||
| 21/13 | 701.7817 | ||
| 19/10 | 702.2399 | ||
| 21/11 | 703.8926 | ||
| 13/7 | 704.0426 | ||
| 11/7 | 704.3770 |
Helenus
| Edo generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 7\12 | 700.0000 | Lower bound of 9- and 11-odd-limit diamond monotone | |
| 19/16 | 700.8290 | 1/3 undevicesimal schisma | |
| 11/7 | 701.0942 | ||
| 19/12 | 701.1105 | 1/4 undevicesimal schisma | |
| 21/11 | 701.1149 | ||
| 13/7 | 701.4894 | ||
| 21/13 | 701.5127 | ||
| 38\65 | 701.5385 | 65d val, lower bound of 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 11/10 | 701.5907 | ||
| 15/11 | 701.6066 | ||
| 11/8 | 701.6227 | ||
| 11/6 | 701.6335 | ||
| 11/9 | 701.6435 | 11-, 13-, and 15-odd-limit minimax | |
| 15/8 | 701.6759 | 1/7 schisma | |
| 19/11 | 701.7109 | ||
| 5/4 | 701.7108 | 1/8 schisma | |
| 25/24 | 701.7252 | 2/17 schisma | |
| 5/3 | 701.7379 | 5-odd-limit minimax, 1/9 schisma | |
| 9/5 | 701.7596 | 1/10 schisma | |
| 81/80 | 701.7922 | 1/12 schisma | |
| 13/8 | 701.8022 | ||
| 13/12 | 701.8067 | ||
| 13/9 | 701.8109 | ||
| 13/10 | 701.8314 | ||
| 15/13 | 701.8362 | ||
| 31\53 | 701.8868 | Upper bound of 11-, 13-, 15-odd-limit, 2.3.5.7.11.13.19 subgroup 19- and 21-odd-limit diamond monotone | |
| 19/13 | 701.8995 | ||
| 3/2 | 701.9550 | Pythagorean tuning | |
| 36/35 | 702.0321 | ||
| 9/7 | 702.1928 | 9-odd-limit minimax, 1/16 septimal schisma | |
| 7/6 | 702.2086 | 7-odd-limit minimax, 1/15 septimal schisma | |
| 49/48 | 702.2174 | 2/29 septimal schisma | |
| 7/4 | 702.2267 | 1/14 septimal schisma | |
| 19/10 | 702.2399 | ||
| 21/16 | 702.2476 | 1/13 septimal schisma | |
| 64/63 | 702.2720 | 1/12 septimal schisma | |
| 19/15 | 702.3111 | ||
| 24\41 | 702.4390 | 41ef val | |
| 19/14 | 702.6079 | ||
| 21/19 | 702.6732 | ||
| 15/14 | 702.7775 | ||
| 7/5 | 702.9146 | ||
| 21/20 | 703.1066 | ||
| 17\29 | 703.4483 | 29eeff val, upper bound of 9-odd-limit diamond monotone | |
| 13/11 | 703.5968 |
* Besides the octave