41edo
| ← 40edo | 41edo | 42edo → |
(convergent)
41 equal divisions of the octave (abbreviated 41edo or 41ed2), also called 41-tone equal temperament (41tet) or 41 equal temperament (41et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 41 equal parts of about 29.3 ¢ each. Each step represents a frequency ratio of 21/41, or the 41st root of 2.
Theory
41edo is the second smallest equal division (after 29edo) whose perfect fifth is closer to just intonation than that of 12edo, and is the seventh zeta integral edo, after 31; it is not, however, a zeta gap edo. This has to do with the fact that it can deal with the 11-limit fairly well, and perhaps the 13-limit. In fact, it is consistent to the 15-odd-limit, or the no-17's 21-odd-limit. All of its intervals between 100 and 1100 cents in size are 15-odd-limit consonances, although its ~13/10 is 14 cents sharp and arguably manifests itself as 21/16 rather than 13/10.
41edo is perhaps the smallest edo with a satisfactory model of the 9-odd-limit, not only because it is the smallest one to tune the 9-odd-limit distinctly consistent, but it is also consistent to distance 2. In other words, all intervals in the 9-odd-limit are more in-tune than out of tune. It is also the first edo to either match or improve on 12edo's accuracy of every harmonic up to the 16th, and no interval from the 11-odd-limit except for 11/10 and 20/11 is represented with more than 10 cents of error in it. Apart from the full 13-limit, it is even more prominent as a 2.3.5.7.11.19.29.31 subgroup temperament for its size.
41edo is used by the Kite Guitar, see below in #Instruments.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +0.5 | -5.8 | -3.0 | +4.8 | +8.3 | +12.1 | -4.8 | -13.6 |
| Relative (%) | +0.0 | +1.7 | -19.9 | -10.2 | +16.3 | +28.2 | +41.4 | -16.5 | -46.6 | |
| Steps (reduced) |
41 (0) |
65 (24) |
95 (13) |
115 (33) |
142 (19) |
152 (29) |
168 (4) |
174 (10) |
185 (21) | |
| Harmonic | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -5.2 | -3.6 | +12.1 | +10.0 | -14.0 | +7.7 | +4.5 | -5.5 | -4.7 |
| Relative (%) | -17.7 | -12.2 | +41.2 | +34.0 | -47.7 | +26.2 | +15.5 | -18.8 | -16.0 | |
| Steps (reduced) |
199 (35) |
203 (39) |
214 (9) |
220 (15) |
222 (17) |
228 (23) |
235 (30) |
241 (36) |
243 (38) | |
As a tuning of other temperaments
41edo can be seen as a tuning of the garibaldi temperament[1][2], as well as miracle, magic, superkleismic, and multiple temperaments in the tetracot family.
Various 13-limit magic extensions are supported by 41: 13-limit magic, and less successfully necromancy and witchcraft, all merge into one in 41edo tuning. The 41f val provides a superb tuning for sorcery, giving a less-complex version of the 13-limit, and the 41ef val likewise works well for telepathy; telepathy and sorcery merging into one however not in 41edo but in 22edo.
41edo is also a great tetracot tuning, and works as an alternative to 34edo, providing proper approximations to the 7th and 11th harmonic at the cost of the 13th, and supporting monkey, bunya and octacot simultaneously. All three of these extend to the 11-limit by way of interpreting the flat 10/9 as an 11/10 by tempering out 100/99. This equivalence is especially useful in 41edo, wherein this comma-flat whole tone a.k.a. the second of Tetracot[7] can also be more accurately interpreted as 21/19—which is equated with 32/29 above 31/28 below (both very near)—providing an explanation of the accuracy of primes 29 and 31 so that it is a uniquely good/versatile choice for interpreting the harmony of tetracot.
A step of 41edo is close and consistently mapped to 64/63, the septimal comma.
Subsets and supersets
41edo is the 13th prime edo, following 37edo and coming before 43edo. It does not contain any nontrivial subset edos, though it contains 41ed4.
205edo, which slices each step of 41edo into five, corrects some approximations of 41edo to near-just quality. As such, 41edo forms the foundation of the H-System, which uses the scale degrees of 41edo as the basic 13-limit intervals requiring fine tuning ±1 average JND from the 41edo circle in 205edo. Its step of 1\205 is called a mem.
2460edo has potential for a 41edo analog to cents. It divides the 41edo step into 60 equal parts, and 60 is a highly composite (a.k.a. antiprime) number, so it contains many other multiples of 41edo, including 205edo, and also contains 12edo among other equal tunings. It also accurately represents mode 14 of the harmonic series, as it is consistent all the way up to the 27-odd-limit. This allows for precise detunings in a 41-tone framework to approximate pure just intonation more closely, especially for some higher harmonics. Its step of 1\2460 is called a mina.
Intervals
| # | Cents | Approximate ratios* | Ups and downs notation (EUs: v4A1 and ^d2) |
SKULO notation (K or S = 1, U = 2) | Kite's solfege |
Andrew's solfege | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1/1 | perfect unison | P1 | D | perfect unison | P1 | D | Da | Do |
| 1 | 29.3 | 49/48, 50/49, 64/63, 81/80 | up-unison | ^1 | ^D | comma-wide unison, super unison | K1/S1 | KD, SD | Du | Di |
| 2 | 58.5 | 25/24, 28/27, 33/32, 36/35 | dup-unison, downminor 2nd | ^^1, vm2 | ^^D, vEb | subminor 2nd, classic aug unison, uber unison | sm2, kkA1, U1 | sEb, kkD#, UD | Fro | Ro |
| 3 | 87.8 | 19/18, 20/19, 21/20, 22/21 | down-aug 1sn, minor 2nd | vA1, m2 | vD#, Eb | minor 2nd, comma-narrow augmented unison | m2, kA1 | Eb, kD# | Fra | Rih |
| 4 | 117.1 | 14/13, 15/14, 16/15 | augmented 1sn, upminor 2nd | A1, ^m2 | D#, ^Eb | classic minor 2nd, augmented unison | Km2, A1 | KEb, D# | Fru | Ra |
| 5 | 146.3 | 12/11, 13/12 | mid 2nd | ~2 | ^D#, vvE | neutral second, super augmented unison | N2, SA1 | UEb/uE, sD# | Ri | Ru |
| 6 | 175.6 | 10/9, 11/10, 21/19 | downmajor 2nd | vM2 | vE | classic/comma-wide major 2nd | kM2 | kE | Ro | Reh |
| 7 | 204.9 | 9/8 | major 2nd | M2 | E | major 2nd | M2 | E | Ra | Re |
| 8 | 234.1 | 8/7, 15/13 | upmajor 2nd | ^M2 | ^E | supermajor 2nd | SM2 | SE | Ru | Ri |
| 9 | 263.4 | 7/6, 22/19 | downminor 3rd | vm3 | vF | subminor 3rd | sm3 | sF | No | Ma |
| 10 | 292.7 | 13/11, 19/16, 32/27 | minor 3rd | m3 | F | minor 3rd | m3 | F | Na | Meh |
| 11 | 322.0 | 6/5 | upminor 3rd | ^m3 | ^F | classicminor 3rd | Km3 | KF | Nu | Me |
| 12 | 351.2 | 11/9, 16/13 | mid 3rd | ~3 | ^^F, vGb | neutral 3rd, sub diminished 4th | N3, sd4 | UF/uF#, sGb | Mi | Mu |
| 13 | 380.5 | 5/4, 26/21 | downmajor 3rd | vM3 | vF#, Gb | classic major 3rd, diminished 4th | kM3, d4 | kF#, Gb | Mo | Mi |
| 14 | 409.8 | 14/11, 19/15, 24/19 | major 3rd | M3 | F#, ^Gb | major 3rd, comma-wide diminished 4th | M3, Kd4 | F#, KGb | Ma | Maa |
| 15 | 439.0 | 9/7, 32/25 | upmajor 3rd | ^M3 | ^F#, vvG | supermajor 3rd, classic diminished 4th | SM3, KKd4 | SF#, KKGb | Mu | Mo |
| 16 | 468.3 | 21/16, 13/10 | down-4th | v4 | vG | sub 4th | s4 | sG | Fo | Fe |
| 17 | 497.6 | 4/3 | perfect 4th | P4 | G | perfect 4th | P4 | G | Fa | Fa |
| 18 | 526.8 | 15/11, 19/14, 27/20 | up-4th | ^4 | ^G | comma-wide 4th | K4 | KG | Fu | Fih |
| 19 | 556.1 | 11/8, 18/13, 26/19 | mid-4th, downdim 5th | ~4, vd5 | ^^G, vAb | uber/neutral 4th, classic augmented 4th | U4/N4, kkA4 | UG, kkG# | Fi/Sho | Fu |
| 20 | 585.4 | 7/5, 45/32 | downaug 4th, dim 5th | vA4, d5 | vG#, Ab | comma-narrow augmented 4th, diminished 5th | kA4/d5 | kG#, Ab | Po/Sha | Fi |
| 21 | 614.6 | 10/7, 64/45 | aug 4th, updim 5th | A4, ^d5 | G#, ^Ab | augmented 4th, comma-wide diminished 5th | A4/Kd5 | G#, KAb | Pa/Shu | Se |
| 22 | 643.9 | 13/9, 16/11, 19/13 | mid-5th, upaug 4th | ~5, ^A4 | ^G#, vvA | unter/neutral 5th, classic diminished 5th | u5/N5, KKd5 | uA, KKAb | Pu/Si | Su |
| 23 | 673.2 | 22/15, 28/19, 40/27 | down-5th | v5 | vA | comma-narrow 5th | k5 | kA | So | Sih |
| 24 | 702.4 | 3/2 | perfect 5th | P5 | A | perfect 5th | P5 | A | Sa | Sol |
| 25 | 731.7 | 20/13, 32/21 | up-5th | ^5 | ^A | super 5th | S5 | SA | Su | Si |
| 26 | 761.0 | 14/9, 25/16 | downminor 6th | vm6 | ^^A, vBb | subminor 6th, classic augmented 5th | sm6 | sBb, kkA# | Flo | Lo |
| 27 | 790.2 | 11/7, 19/12, 30/19 | minor 6th | m6 | vA#, Bb | minor 6th, comma-narrow augmented 5th | m6 | Bb, kA# | Fla | Leh |
| 28 | 819.5 | 8/5, 21/13 | upminor 6th | ^m6 | A#, ^Bb | classic minor 6th, augmented 5th | Km6, A5 | KBb, A# | Flu | Le |
| 29 | 848.8 | 13/8, 18/11 | mid 6th | ~6 | ^A#, vvB | neutral 6th, super augmented 5th | N6 | UBb/uB, sA# | Li | Lu |
| 30 | 878.0 | 5/3 | downmajor 6th | vM6 | vB | classic major 6th | kM6 | kB | Lo | La |
| 31 | 907.3 | 22/13, 27/16, 32/19 | major 6th | M6 | B | major 6th | M6 | B | La | Laa |
| 32 | 936.6 | 12/7, 19/11 | upmajor 6th | ^M6 | ^B | supermajor 6th | SM6 | SB | Lu | Li |
| 33 | 965.9 | 7/4, 26/15 | downminor 7th | vm7 | vC | subminor 7th | sm7 | sC | Tho | Ta |
| 34 | 995.1 | 16/9 | minor 7th | m7 | C | minor 7th | m7 | C | Tha | Teh |
| 35 | 1024.4 | 9/5, 20/11, 38/21 | upminor 7th | ^m7 | ^C | classic/comma-wide minor seventh | Km7 | KC | Thu | Te |
| 36 | 1053.7 | 11/6, 24/13 | mid 7th | ~7 | ^^C, vDb | neutral 7th, sub diminished 8ve | N7 | UC/uC#, sDb | Ti | Tu |
| 37 | 1082.9 | 13/7, 15/8, 28/15 | downmajor 7th | vM7 | vC#, Db | classic major 7th, diminished 8ve | kM7, d8 | kC#, Db | To | Ti |
| 38 | 1112.2 | 19/10, 21/11, 36/19, 40/21 | major 7th | M7 | C#, ^Db | major 7th, comma-wide diminished 8ve | M7, Kd8 | C#, KDb | Ta | Taa |
| 39 | 1141.5 | 27/14, 35/18, 48/25, 64/33 | upmajor 7th | ^M7 | ^C#, vvD | supermajor 7th, classic dim 8ve, unter 8ve | SM7, KKd8, U8 | SC#, KKDb, u8 | Tu | To |
| 40 | 1170.7 | 49/25, 63/32, 96/49, 160/81 | dim 8ve | v8 | vD | comma-narrow 8ve, sub 8ve | k8/s8 | kD, sD | Do | Da |
| 41 | 1200.0 | 2/1 | perfect 8ve | P8 | D | perfect 8ve | P8 | D | Da | Do |
* Based on treating 41edo as a 2.3.5.7.11.13.19 subgroup temperament; other approaches are possible.
Interval quality and chord names in color notation
Combining ups and downs notation with color notation, qualities can be loosely associated with colors:
| Quality | Color | Monzo format | Examples |
|---|---|---|---|
| downminor | zo | (a, b, 0, 1) | 7/6, 7/4 |
| minor | fourthward wa | (a, b) with b < -1 | 32/27, 16/9 |
| upminor | gu | (a, b, -1) | 6/5, 9/5 |
| mid | ilo | (a, b, 0, 0, 1) | 11/9, 11/6 |
| " | lu | (a, b, 0, 0, -1) | 12/11, 18/11 |
| downmajor | yo | (a, b, 1) | 5/4, 5/3 |
| major | fifthward wa | (a, b) with b > 1 | 9/8, 27/16 |
| upmajor | ru | (a, b, 0, -1) | 9/7, 12/7 |
All 41edo chords can be named using ups and downs. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are. Here are the zo, gu, ilo, yo and ru triads:
| Color of the 3rd | JI chord | Notes as edosteps | Notes of C chord | Written name | Spoken name |
|---|---|---|---|---|---|
| zo (7-over) | 6:7:9 | 0-9-24 | C vEb G | Cvm | C downminor |
| gu (5-under) | 10:12:15 | 0-11-24 | C ^Eb G | C^m | C upminor |
| ilo (11-over) | 18:22:27 | 0-12-24 | C vvE G | C~ | C mid |
| yo (5-over) | 4:5:6 | 0-13-24 | C vE G | Cv | C downmajor or C down |
| ru (7-under) | 14:18:21 | 0-15-24 | C ^E G | C^ | C upmajor or C up |
Other common triads are
- 0-10-20 = D F Ab = Dd = D dim
- 0-10-21 = D F ^Ab = Dd(^5) = D dim up-five
- 0-10-22 = D F vvA = Dm(~5) = D minor mid-five
- 0-10-23 = D F vA = Dm(v5) = D minor down-five
- 0-10-24 = D F A = Dm = D minor
- 0-14-24 = D F# A = D = D or D major
- 0-14-25 = D F# ^A = D(^5) = D up-five
- 0-14-26 = D F# ^^A = D(^^5) = D half-aug
- 0-14-27 = D F# vA# = Da(v5) = D aug down-five or perhaps D(v#5) = D downsharp-five
- 0-14-28 = D F# A# = Da = D aug
For a more complete list, see 41edo Chord Names and Ups and downs notation #Chords and chord progressions.
Notations
Ups and downs notation
41edo can be notated with ups and downs, spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that dup is equivalent to dudsharp and dud is equivalent to dupflat.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||
| Flat symbol | |
|
41edo can also be notated with quarter-tone accidentals and ups and downs. This can be done by combining sharps and flats with arrows borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
|
| ||
| Flat symbol | |
|
|
|
|
|
The notes within an octave from A are thus:
A, B ![]() , A
, A ![]() , B♭, A♯, B
, B♭, A♯, B ![]() , A
, A ![]() , B, C
, B, C ![]() , B
, B ![]() , C, D
, C, D ![]() , C
, C ![]() , D♭, C♯, D
, D♭, C♯, D ![]() , C
, C ![]() , D, E
, D, E ![]() , D
, D ![]() , E♭, D♯, E
, E♭, D♯, E ![]() , D
, D ![]() , E, F
, E, F ![]() , E
, E ![]() , F, G
, F, G ![]() , F
, F ![]() , G♭, F♯, G
, G♭, F♯, G ![]() , F
, F ![]() , G, A
, G, A ![]() , G
, G ![]() , A♭, G♯, A
, A♭, G♯, A ![]() , G
, G ![]() , A
, A
Red-Blue notation
A red-note/blue-note system, similar to the one proposed for 36edo, is another option for notating 41edo. This is a special case of Kite's color notation, treating 41edo as a temperament of the 2.3.7 subgroup. We have the "white key" albitonic notes A–G (7 in total), the "black key" sharps and flats (10 in total), a "red" and "blue" version of each albitonic note (14 in total), a "red" (dark red?) version of each sharp and a "blue" (dark blue?) version of each flat (10 in total), adding up to 41. This would result in quite a colorful keyboard! Note that there are no red flats or blue sharps. Using this nomenclature the notes are:
A , A , B♭ , B♭ , A♯ , A♯ , B , B , B , C , C , C , D♭ , D♭ , C♯ , C♯ , D , D , D , E♭ , E♭ , D♯ , D♯ , E , E , E , F , F , F , G♭ , G♭ , F♯ , F♯ , G , G , G , A♭ , A♭ , G♯ , G♯ , A , A
Interval classes could also be named by analogy. The natural, colorless, or gray interval classes are the Pythagorean ones (which show up in the standard diatonic scale), while "red" and "blue" versions are one step higher or lower. Gray thirds, sixths, and sevenths are usually more dissonant than their colorful counterparts, but the reverse is true of fourths and fifths.
The step size of 41edo is small enough that the smallest interval (the "red/blue unison", seventh-tone, comma, diesis or whatever you want to call it) is actually fairly consonant with most timbres; it resembles a "noticeably out of tune unison" rather than a minor second, and has its own distinct character and appeal.
If "red" is replaced by "up", "blue" by "down", and "neutral" by "mid", and if "gray" is omitted, this notation becomes essentially the same as ups and downs notation. The only difference is the use of minor tritone and major tritone.
Sagittal notation
This notation uses the same sagittal sequence as 34edo.
Evo flavor

Revo flavor

We also have a diagram from the appendix to The Sagittal Songbook by Jacob A. Barton, which gives multiple spellings for each pitch, and up to the double-apotome:
Evo-SZ flavor

Approximation to JI
Interval mappings
The following table shows how 15-odd-limit intervals are represented in 41edo. Prime harmonics are in bold.
As 41edo is consistent in the 15-odd-limit, the mappings by direct approximation and through the patent val are identical.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 3/2, 4/3 | 0.484 | 1.7 |
| 9/8, 16/9 | 0.968 | 3.3 |
| 15/14, 28/15 | 2.370 | 8.1 |
| 7/5, 10/7 | 2.854 | 9.8 |
| 7/4, 8/7 | 2.972 | 10.2 |
| 7/6, 12/7 | 3.456 | 11.8 |
| 13/11, 22/13 | 3.473 | 11.9 |
| 11/9, 18/11 | 3.812 | 13.0 |
| 9/7, 14/9 | 3.940 | 13.5 |
| 11/6, 12/11 | 4.296 | 14.7 |
| 11/8, 16/11 | 4.780 | 16.3 |
| 15/8, 16/15 | 5.342 | 18.3 |
| 5/4, 8/5 | 5.826 | 19.9 |
| 5/3, 6/5 | 6.310 | 21.6 |
| 9/5, 10/9 | 6.794 | 23.2 |
| 13/9, 18/13 | 7.285 | 24.9 |
| 11/7, 14/11 | 7.752 | 26.5 |
| 13/12, 24/13 | 7.769 | 26.5 |
| 13/8, 16/13 | 8.253 | 28.2 |
| 15/11, 22/15 | 10.122 | 34.6 |
| 11/10, 20/11 | 10.606 | 36.2 |
| 13/7, 14/13 | 11.225 | 38.4 |
| 15/13, 26/15 | 13.595 | 46.4 |
| 13/10, 20/13 | 14.079 | 48.1 |
Relationship to 12edo
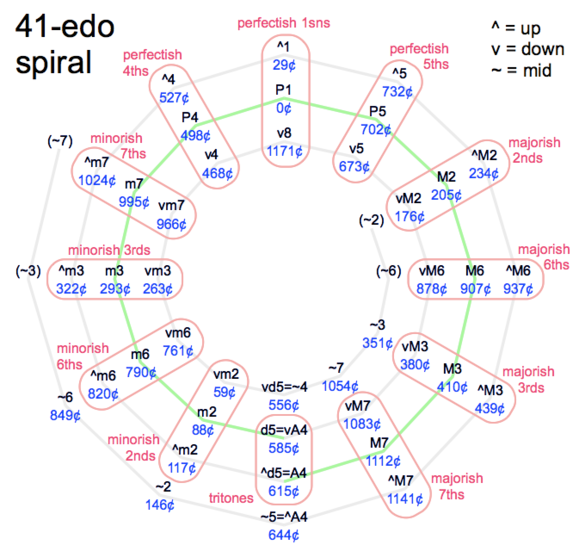
41edo’s circle of 41 fifths can be bent into a 12-spoked "spiral of fifths". This is possible because 24\41 is on the 7\12 kite in the scale tree. Stated another way, it is possible because the absolute value of 41edo's dodeca-sharpness (edosteps per Pythagorean comma) is 1.
This "spiral of fifths" can be a useful construct for introducing 41edo to musicians unfamiliar with microtonal music. It may help composers and musicians to make visual sense of the notation, and to understand what size of a jump is likely to land them where compared to 12edo.
There are 12 "-ish" categories, where "-ish" means ±1 edostep. The 6 mid intervals are uncategorized, since they are all so far from 12edo.
The two innermost and two outermost intervals on the spiral are duplicates, reflecting the fact that it is a repeating circle at heart and the spiral shape is only a helpful illusion.
The same spiral, but with notes not intervals:
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [65 -41⟩ | [⟨41 65]] | −0.153 | 0.15 | 0.52 |
| 2.3.5 | 3125/3072, 20000/19683 | [⟨41 65 95]] | +0.734 | 1.26 | 4.31 |
| 2.3.5.7 | 225/224, 245/243, 1029/1024 | [⟨41 65 95 115]] | +0.815 | 1.10 | 3.76 |
| 2.3.5.7.11 | 100/99, 225/224, 243/242, 245/242 | [⟨41 65 95 115 142]] | +0.375 | 1.32 | 4.51 |
| 2.3.5.7.11.13 | 100/99, 105/104, 144/143, 196/195, 243/242 | [⟨41 65 95 115 142 152]] | −0.060 | 1.55 | 5.29 |
| 2.3.5.7.11.13.19 | 100/99, 105/104, 133/132, 144/143, 171/169, 196/195 | [⟨41 65 95 115 142 152 174]] | +0.111 | 1.49 | 5.10 |
- 41et is lower in relative error than any previous equal temperaments in the 3-, 13- and 19-limit. The next equal temperaments doing better in these subgroups are 53, 53, and 46, respectively. It is even more prominent in the 2.3.5.7.11.19 and 2.3.5.7.11.13.19 subgroup. The next equal temperaments doing better in these subgroups are 72 and 53, respectively.
Commas
41et tempers out the following commas using its patent val, ⟨41 65 95 115 142 152 168 174 185 199 203].
| Prime limit |
Ratio[3] | Cents | Monzo | Color name | Name(s) | |
|---|---|---|---|---|---|---|
| 3 | (40 digits) | 19.84 | [65 -41⟩ | Wa-41 | 41-edo | 41-comma |
| 5 | (14 digits) | 57.27 | [-5 -10 9⟩ | Tritriyo | y9 | Shibboleth comma |
| 5 | (16 digits) | 31.57 | [-25 7 6⟩ | Lala-tribiyo | LLy3 | Ampersand comma |
| 5 | 3125/3072 | 29.61 | [-10 -1 5⟩ | Laquinyo | Ly5 | Magic comma |
| 5 | (10 digits) | 27.66 | [5 -9 4⟩ | Saquadyo | sy4 | Tetracot comma |
| 5 | (18 digits) | 25.71 | [20 -17 3⟩ | Sasa-triyo | ssy3 | Roda |
| 5 | (10 digits) | 1.95 | [-15 8 1⟩ | Layo | Ly | Schisma |
| 7 | (10 digits) | 35.37 | [0 -7 6 -1⟩ | Rutribiyo | ry6 | Arcturus comma, great BP diesis |
| 7 | (18 digits) | 22.41 | [-10 7 8 -7⟩ | Lasepru-aquadbiyo | Lr7y8 | Blackjackisma |
| 7 | 875/864 | 21.90 | [-5 -3 3 1⟩ | Zotriyo | zy3 | Keema |
| 7 | 3125/3087 | 21.18 | [0 -2 5 -3⟩ | Triru-aquinyo | r3y5 | Gariboh comma |
| 7 | (12 digits) | 19.95 | [10 -11 2 1⟩ | Sazoyoyo | szyy | Tolerma |
| 7 | (10 digits) | 16.14 | [-15 3 2 2⟩ | Labizoyo | Lzzyy | Mirwomo comma |
| 7 | 245/243 | 14.19 | [0 -5 1 2⟩ | Zozoyo | zzy | Sensamagic comma |
| 7 | 4000/3969 | 13.47 | [5 -4 3 -2⟩ | Rurutriyo | rry3 | Octagar comma |
| 7 | (12 digits) | 9.15 | [-15 0 -2 7⟩ | Lasepzo-agugu | Lz7gg | Quince comma |
| 7 | 1029/1024 | 8.43 | [-10 1 0 3⟩ | Latrizo | Lz3 | Gamelisma |
| 7 | 225/224 | 7.71 | [-5 2 2 -1⟩ | Ruyoyo | ryy | Marvel comma |
| 7 | (10 digits) | 6.99 | [0 3 4 -5⟩ | Quinru-aquadyo | r5y4 | Mirkwai comma |
| 7 | (10 digits) | 6.48 | [5 -7 -1 3⟩ | Satrizo-agu | sz3g | Hemimage comma |
| 7 | 5120/5103 | 5.76 | [10 -6 1 -1⟩ | Saruyo | sry | Hemifamity comma |
| 7 | (16 digits) | 3.80 | [25 -14 0 -1⟩ | Sasaru | ssr | Garischisma |
| 7 | 2401/2400 | 0.72 | [-5 -1 -2 4⟩ | Bizozogu | z4gg | Breedsma |
| 11 | (12 digits) | 29.72 | [15 0 1 0 -5⟩ | Saquinlu-ayo | s1u5y | Thuja comma |
| 11 | 245/242 | 21.33 | [-1 0 1 2 -2⟩ | Luluzozoyo | 1uuzzy | Frostma |
| 11 | 100/99 | 17.40 | [2 -2 2 0 -1⟩ | Luyoyo | 1uyy | Ptolemisma |
| 11 | 1344/1331 | 16.83 | [6 1 0 1 -3⟩ | Trilu-azo | 1u3z | Hemimin comma |
| 11 | 896/891 | 9.69 | [7 -4 0 1 -1⟩ | Saluzo | s1uz | Pentacircle comma |
| 11 | (10 digits) | 8.39 | [16 0 0 -2 -3⟩ | Satrilu-aruru | s1u3rr | Orgonisma |
| 11 | 243/242 | 7.14 | [-1 5 0 0 -2⟩ | Lulu | 1uu | Rastma |
| 11 | 385/384 | 4.50 | [-7 -1 1 1 1⟩ | Lozoyo | 1ozg | Keenanisma |
| 11 | 441/440 | 3.93 | [-3 2 -1 2 -1⟩ | Luzozogu | 1uzzg | Werckisma |
| 11 | 1375/1372 | 3.78 | [-2 0 3 -3 1⟩ | Lotriruyo | 1or3y | Moctdel comma |
| 11 | 540/539 | 3.21 | [2 3 1 -2 -1⟩ | Lururuyo | 1urry | Swetisma |
| 11 | 3025/3024 | 0.57 | [-4 -3 2 -1 2⟩ | Loloruyoyo | 1ooryy | Lehmerisma |
| 11 | (12 digits) | 0.15 | [-1 2 -4 5 -2⟩ | Luluquinzo-aquadgu | 1uuz5g4 | Odiheim comma |
| 13 | 343/338 | 25.42 | [-1 0 0 3 0 -2⟩ | Thuthutrizo | 3uuz3 | |
| 13 | 105/104 | 16.57 | [-3 1 1 1 0 -1⟩ | Thuzoyo | 3uzy | Animist comma |
| 13 | (10 digits) | 14.61 | [12 -7 0 1 0 -1⟩ | Sathuzo | s3uz | Secorian comma |
| 13 | 275/273 | 12.64 | [0 -1 2 -1 1 -1⟩ | Thuloruyoyo | 3u1oryy | Gassorma |
| 13 | 144/143 | 12.06 | [4 2 0 0 -1 -1⟩ | Thulu | 3u1u | Grossma |
| 13 | 196/195 | 8.86 | [2 -1 -1 2 0 -1⟩ | Thuzozogu | 3uzzg | Mynucuma |
| 13 | 640/637 | 8.13 | [7 0 1 -2 0 -1⟩ | Thururuyo | 3urry | Huntma |
| 13 | 1188/1183 | 7.30 | [2 3 0 -1 1 -2⟩ | Thuthuloru | 3uu1or | Kestrel comma |
| 13 | 31213/31104 | 6.06 | [-7 -5 0 4 0 1⟩ | Thoquadzo | 3oz43 | Praveensma |
| 13 | 325/324 | 5.34 | [-2 -4 2 0 0 1⟩ | Thoyoyo | 3oyy | Marveltwin comma |
| 13 | 352/351 | 4.93 | [5 -3 0 0 1 -1⟩ | Thulo | 3u1o | Major minthma |
| 13 | 364/363 | 4.76 | [2 -1 0 1 -2 1⟩ | Tholuluzo | 3o1uuz | Minor minthma |
| 13 | 847/845 | 4.09 | [0 0 -1 1 2 -2⟩ | Thuthulolozogu | 3uu1oozg | Cuthbert comma |
| 13 | 729/728 | 2.38 | [-3 6 0 -1 0 -1⟩ | Lathuru | L3ur | Squbema |
| 13 | 2080/2079 | 0.83 | [5 -3 1 -1 -1 1⟩ | Tholuruyo | 3o1ury | Ibnsinma |
| 13 | 4096/4095 | 0.42 | [12 -2 -1 -1 0 -1⟩ | Sathurugu | s3urg | Schismina |
| 13 | 6656/6655 | 0.26 | [9 0 -1 0 -3 1⟩ | Thotrilo-agu | 3u1o3g2 | Jacobin comma |
| 13 | (10 digits) | 0.16 | [3 -2 0 -1 3 -2⟩ | Thuthutrilo-aru | 3uu1o3r | Harmonisma |
| 17 | 2187/2176 | 8.73 | [-7 7 0 0 0 0 -1⟩ | Lasu | L17u | Septendecimal schisma |
| 17 | 256/255 | 6.78 | [8 -1 -1 0 0 0 -1⟩ | Sugu | 17ug | Charisma |
| 17 | 715/714 | 2.42 | [-1 -1 1 -1 1 1 -1⟩ | Sutholoruyo | 17u3o1ory | Septendecimal bridge comma |
| 19 | 210/209 | 8.26 | [1 1 1 1 -1 0 0 -1⟩ | Nuluzoyo | 19u1uzy | Spleen comma |
| 19 | 361/360 | 4.80 | [-3 -2 -1 0 0 0 0 2⟩ | Nonogu | 19oog2 | Go comma |
| 19 | 513/512 | 3.38 | [-9 3 0 0 0 0 0 1⟩ | Lano | L19o | Boethius' comma |
| 19 | 1216/1215 | 1.42 | [6 -5 -1 0 0 0 0 1⟩ | Sanogu | s19og | Eratosthenes' comma |
| 23 | 736/729 | 16.54 | [5 -6 0 0 0 0 0 0 1⟩ | Satwetho | s23o | Vicesimotertial comma |
| 29 | 145/144 | 11.98 | [-4 -2 1 0 0 0 0 0 0 1⟩ | Twenoyo | 29oy | 29th-partial chroma |
Rank-2 temperaments
| Degree | Cents | Temperament(s) | Pergen | Mos scales |
|---|---|---|---|---|
| 1 | 29.27 | Slendi | (P8, P4/17) | |
| 2 | 58.54 | Hemimiracle Dodecacot |
(P8, P5/12) | 21-tone mos |
| 3 | 87.80 | Octacot | (P8, P5/8) | 14-tone mos: 3 3 3 3 3 3 3 3 3 3 3 3 3 2 |
| 4 | 117.07 | Miracle | (P8, P5/6) | 11-tone mos: 4 4 4 4 4 4 4 4 4 4 1 |
| 5 | 146.34 | BPS / bohpier | (P8, P12/13) | 20-tone mos |
| 6 | 175.61 | Tetracot / bunya / monkey Sesquiquartififths / sesquart |
(P8, P5/4) | 13-tone mos: 1 5 1 5 1 5 1 5 5 1 5 1 5 |
| 7 | 204.88 | Baldy Quadrimage |
(P8, c3P4/20) | 11-tone mos: 6 1 6 6 1 6 1 6 1 6 1 |
| 8 | 234.15 | Slendric / rodan / guiron | (P8, P5/3) | 11-tone mos: 7 1 7 1 7 1 7 1 1 7 1 |
| 9 | 263.41 | Septimin | (P8, ccP4/11) | 9-tone mos: 5 4 5 5 4 5 4 5 4 |
| 10 | 292.68 | Quasitemp | (P8, c3P4/14) | 29-tone mos |
| 11 | 321.95 | Superkleismic | (P8, ccP4/9) | 11-tone mos: 5 3 5 3 3 5 3 3 5 3 3 |
| 12 | 351.22 | Hemif / hemififths / salsa Karadeniz |
(P8, P5/2) | 10-tone mos: 5 2 5 5 2 5 5 5 2 5 |
| 13 | 380.49 | Magic / witchcraft Quanharuk |
(P8, P12/5) | 10-tone mos: 2 9 2 2 9 2 2 9 2 2 |
| 14 | 409.76 | Hocum Hocus |
(P8, c3P4/10) | 32-tone mos |
| 15 | 439.02 | Superthird | (P8, c6P5/18) | 11-tone mos: 4 3 4 4 4 3 4 4 3 4 4 |
| 16 | 468.29 | Barbad | (P8, c7P4/19) | 8-tone mos: 7 2 7 7 2 7 7 2 |
| 17 | 497.56 | Helmholtz / garibaldi / cassandra / andromeda Kwai |
(P8, P5) | 12-tone mos: 4 3 4 3 3 4 3 4 3 4 3 4 3 3 |
| 18 | 526.83 | Trismegistus | (P8, c6P5/15) | 9-tone mos: 5 5 3 5 5 5 5 3 5 |
| 19 | 556.10 | Alphorn | (P8, c7P4/16) | 9-tone mos: 3 3 3 10 3 3 3 3 10 |
| 20 | 585.37 | Pluto Merman |
(P8, c3P4/7) |
Octave stretch or compression
Whether there is intonational improvement from octave stretch or compression depends on which subgroup we are focusing on.
For the 5-, 7-, and 11-limit, stretch is advised, though in the case of the 11-limit the stretch should be way milder, whereas for the 13-limit and in particular the 17-limit, little to no stretch or even compression may be suitable for balancing out the sharp and flat tuning tendencies, as is demonstrated in tunings such as 65edt, 106ed6, and 147ed12.
Primes 19, 29, and 31 all tend flat, so stretching will serve again as we take that into account, especially if we use the temperament in any no-17 or no-13 no-17 settings.
What follows is a comparison of stretched- and compressed-octave 41edo tunings.
- Step size: 29.248 ¢, octave size: 1199.17 ¢
Compressing the octave of 41edo by around 0.8 ¢ results in unnoticeably improved primes 11, 17 and 23, but unnoticeably worse primes 2, 3, 5, 7, 13 and 19. This approximates all harmonics up to 16 within 7.6 ¢. The tuning 24edf does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.8 | -0.8 | -1.7 | -7.7 | -1.7 | -5.3 | -2.5 | -1.7 | -8.6 | +1.9 | -2.5 |
| Relative (%) | -2.8 | -2.8 | -5.7 | -26.5 | -5.7 | -18.1 | -8.5 | -5.7 | -29.3 | +6.6 | -8.5 | |
| Steps (reduced) |
41 (17) |
65 (17) |
82 (10) |
95 (23) |
106 (10) |
115 (19) |
123 (3) |
130 (10) |
136 (16) |
142 (22) |
147 (3) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +5.2 | -6.1 | -8.6 | -3.3 | +8.7 | -2.5 | -8.3 | -9.4 | -6.1 | +1.1 | +11.9 | -3.3 |
| Relative (%) | +17.7 | -20.9 | -29.3 | -11.3 | +29.8 | -8.5 | -28.5 | -32.1 | -20.9 | +3.7 | +40.6 | -11.3 | |
| Steps (reduced) |
152 (8) |
156 (12) |
160 (16) |
164 (20) |
168 (0) |
171 (3) |
174 (6) |
177 (9) |
180 (12) |
183 (15) |
186 (18) |
188 (20) | |
- 65edt — step size: 29.261 ¢, octave size: 1199.69 ¢
- 106ed6 — step size: 29.264 ¢, octave size: 1199.81 ¢
- 147ed12 — step size: 29.265 ¢, octave size: 1199.87 ¢
Compressing the octave of 41edo by around 0.2 ¢ results in unnoticeably improved primes 3, 11 and 13, but unnoticeably worse primes 2, 5 and 7. This approximates all harmonics up to 16 within 7.6 ¢. The tunings 147ed12, 106ed6 and 65edt each do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.2 | +0.2 | -0.4 | -6.3 | +0.0 | -3.5 | -0.6 | +0.4 | -6.4 | +4.1 | -0.2 |
| Relative (%) | -0.6 | +0.6 | -1.3 | -21.4 | +0.0 | -12.0 | -1.9 | +1.3 | -22.0 | +14.1 | -0.6 | |
| Steps (reduced) |
41 (41) |
65 (65) |
82 (82) |
95 (95) |
106 (0) |
115 (9) |
123 (17) |
130 (24) |
136 (30) |
142 (36) |
147 (41) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +7.6 | -3.7 | -6.1 | -0.7 | +11.4 | +0.2 | -5.6 | -6.6 | -3.3 | +3.9 | -14.5 | -0.4 |
| Relative (%) | +25.8 | -12.6 | -20.8 | -2.6 | +38.8 | +0.6 | -19.2 | -22.7 | -11.3 | +13.5 | -49.5 | -1.3 | |
| Steps (reduced) |
152 (46) |
156 (50) |
160 (54) |
164 (58) |
168 (62) |
171 (65) |
174 (68) |
177 (71) |
180 (74) |
183 (77) |
185 (79) |
188 (82) | |
- 41edo
- Step size: 29.268 ¢, octave size: 1200.00 ¢
Pure-octaves 41edo approximates all harmonics up to 16 within 8.3 ¢. The octaves of its 13-limit WE and TE tuning differ by less than 0.1 ¢ from pure.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +0.5 | +0.0 | -5.8 | +0.5 | -3.0 | +0.0 | +1.0 | -5.8 | +4.8 | +0.5 |
| Relative (%) | +0.0 | +1.7 | +0.0 | -19.9 | +1.7 | -10.2 | +0.0 | +3.3 | -19.9 | +16.3 | +1.7 | |
| Steps (reduced) |
41 (0) |
65 (24) |
82 (0) |
95 (13) |
106 (24) |
115 (33) |
123 (0) |
130 (7) |
136 (13) |
142 (19) |
147 (24) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +8.3 | -3.0 | -5.3 | +0.0 | +12.1 | +1.0 | -4.8 | -5.8 | -2.5 | +4.8 | -13.6 | +0.5 |
| Relative (%) | +28.2 | -10.2 | -18.3 | +0.0 | +41.4 | +3.3 | -16.5 | -19.9 | -8.5 | +16.3 | -46.6 | +1.7 | |
| Steps (reduced) |
152 (29) |
156 (33) |
160 (37) |
164 (0) |
168 (4) |
171 (7) |
174 (10) |
177 (13) |
180 (16) |
183 (19) |
185 (21) |
188 (24) | |
- Step size: 29.277 ¢, octave size: 1200.35 ¢
Stretching the octave of 41edo by around 0.5 ¢ results in unnoticeably improved primes 5 and 7, but unnoticeably worse primes 2, 3, 11 and 13. This approximates all harmonics up to 16 within 9.6 ¢. Its 11-limit WE tuning and 11-limit TE tuning both do this. So does 184zpi, whose octave is identical to WE within 0.02 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.4 | +1.0 | +0.7 | -5.0 | +1.4 | -2.0 | +1.1 | +2.1 | -4.6 | +6.0 | +1.8 |
| Relative (%) | +1.2 | +3.6 | +2.4 | -17.1 | +4.8 | -6.7 | +3.7 | +7.2 | -15.9 | +20.5 | +6.0 | |
| Step | 41 | 65 | 82 | 95 | 106 | 115 | 123 | 130 | 136 | 142 | 147 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +9.6 | -1.6 | -3.9 | +1.4 | +13.6 | +2.5 | -3.3 | -4.3 | -0.9 | +6.4 | -12.0 | +2.1 |
| Relative (%) | +32.7 | -5.5 | -13.5 | +4.9 | +46.4 | +8.4 | -11.3 | -14.6 | -3.1 | +21.8 | -41.1 | +7.2 | |
| Step | 152 | 156 | 160 | 164 | 168 | 171 | 174 | 177 | 180 | 183 | 185 | 188 | |
- Step size: 29.288 ¢, octave size: 1200.81 ¢
Stretching the octave of 41edo by just under 1 ¢ results in just-noticeably improved primes 5 and 7, but just-noticeably worse primes 11 and 13. This approximates all harmonics up to 16 within 11.2 ¢. Its 7-limit WE tuning and 7-limit TE tuning both do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.8 | +1.8 | +1.6 | -4.0 | +2.6 | -0.7 | +2.4 | +3.5 | -3.1 | +7.6 | +3.4 |
| Relative (%) | +2.8 | +6.0 | +5.5 | -13.5 | +8.8 | -2.4 | +8.3 | +12.1 | -10.7 | +25.9 | +11.5 | |
| Step | 41 | 65 | 82 | 95 | 106 | 115 | 123 | 130 | 136 | 142 | 147 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +11.2 | +0.1 | -2.2 | +3.2 | -13.9 | +4.3 | -1.4 | -2.3 | +1.1 | +8.4 | -10.0 | +4.2 |
| Relative (%) | +38.4 | +0.3 | -7.5 | +11.0 | -47.3 | +14.8 | -4.8 | -8.0 | +3.6 | +28.6 | -34.1 | +14.3 | |
| Step | 152 | 156 | 160 | 164 | 167 | 171 | 174 | 177 | 180 | 183 | 185 | 188 | |
Scales and modes
Lists of 41edo scales
- 41edo modes
- List of MOS scales in 41edo
- The Kite Guitar Scales
- Kite Giedraitis's Categorizations of 41edo Scales
Harmonic scale
41edo is the first edo to do some justice to Mode 8 of the harmonic series, which Dante Rosati calls the "Diatonic Harmonic Series Scale," consisting of overtones 8 through 16 (sometimes made to repeat at the octave).
| Overtones in "Mode 8": | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|
| … as JI Ratio from 1/1: | 1/1 | 9/8 | 5/4 | 11/8 | 3/2 | 13/8 | 7/4 | 15/8 | 2/1 |
| … in cents: | 0 | 203.9 | 386.3 | 551.3 | 702.0 | 840.5 | 968.8 | 1088.3 | 1200.0 |
| Nearest degree of 41edo: | 0 | 7 | 13 | 19 | 24 | 29 | 33 | 37 | 41 |
| … in cents: | 0 | 204.9 | 380.5 | 556.1 | 702.4 | 848.8 | 965.9 | 1082.9 | 1200.0 |
While each overtone of Mode 8 is approximated within a reasonable degree of accuracy, the steps between the intervals are not uniquely represented. (41edo is, after all, a temperament.)
- 7\41 (7 degrees of 41edo) (204.9 cents) stands in for just ratio 9/8 (203.9 cents) – a close match.
- 6\41 (175.6 cents) stands in for both 10/9 (182.4 cents) and 11/10 (165.0 cents).
- 5\41 (146.3 cents) stands in for both 12/11 (150.6 cents) and 13/12 (138.6 cents).
- 4\41 (117.1 cents) stands in for 14/13 (128.3 cents), 15/14 (119.4 cents), and 16/15 (111.7 cents).
The scale in 41, as adjacent steps, thus goes: 7 6 6 5 5 4 4 4.
Nonoctave temperaments
Taking every third degree of 41edo produces a scale extremely close to 88cET or 88-cent equal temperament (or the 8th root of 3:2). Likewise, taking every fifth degree produces a scale very close to the equal-tempered Bohlen–Pierce Scale (or the 13th root of 3). See Relationship between Bohlen–Pierce and octave-ful temperaments, and see this chart:
| 3 degrees of 41edo near 88cET | overlap | 5 degrees of 41edo near BP | ||||
|---|---|---|---|---|---|---|
| 41edo | 88cET | cents | cents | cents | BP | 41edo |
| 0 | 0 | 0 | 0 | 0 | ||
| 3 | 1 | 87.8 | ||||
| 146.3 | 1 | 5 | ||||
| 6 | 2 | 175.6 | ||||
| 9 | 3 | 263.4 | ||||
| 292.7 | 2 | 10 | ||||
| 12 | 4 | 351.2 | ||||
| 15 | 5 | 439.0 | 3 | 15 | ||
| 18 | 6 | 526.8 | ||||
| 585.4 | 4 | 20 | ||||
| 21 | 7 | 614.6 | ||||
| 24 | 8 | 702.4 | ||||
| 731.7 | 5 | 25 | ||||
| 27 | 9 | 790.2 | ||||
| 30 | 10 | 878.0 | 6 | 30 | ||
| 33 | 11 | 965.9 | ||||
| 1024.4 | 7 | 35 | ||||
| 36 | 12 | 1053.7 | ||||
| 39 | 13 | 1141.5 | ||||
| 1170.7 | 8 | 40 | ||||
| [ second octave ] | ||||||
| 1 | 14 | 29.2 | ||||
| 4 | 15 | 117.1 | 9 | 4 | ||
| 7 | 16 | 204.9 | ||||
| 263.4 | 10 | 9 | ||||
| 10 | 17 | 292.7 | ||||
| 13 | 18 | 380.5 | ||||
| 409.8 | 11 | 14 | ||||
| 16 | 19 | 468.3 | ||||
| 19 | 20 | 556.1 | 12 | 19 | ||
| 22 | 21 | 643.9 | ||||
| 702.4 | 13 | 24 | ||||
| 25 | 22 | 731.7 | ||||
| 28 | 23 | 819.5 | ||||
| 848.8 | 14 | 29 | ||||
| 31 | 24 | 907.3 | ||||
| 34 | 25 | 995.1 | 15 | 34 | ||
| 37 | 26 | 1082.9 | ||||
| 1141.5 | 16 | 39 | ||||
| 40 | 27 | 1170.7 | ||||
| [ third octave ] | ||||||
| 2 | 28 | 58.5 | ||||
| 87.8 | 17 | 3 | ||||
| 5 | 29 | 146.3 | ||||
| 8 | 30 | 234.1 | 18 | 8 | ||
| 11 | 31 | 322.0 | ||||
| 380.5 | 19 | 13 | ||||
| 14 | 32 | 409.8 | ||||
| 17 | 33 | 497.6 | ||||
| 526.8 | 20 | 18 | ||||
| 20 | 34 | 585.3 | ||||
| 23 | 35 | 673.2 | 21 | 23 | ||
| 26 | 36 | 761.0 | ||||
| 819.5 | 22 | 28 | ||||
| 29 | 37 | 848.8 | ||||
| 32 | 38 | 936.6 | ||||
| 965.9 | 23 | 33 | ||||
| 35 | 39 | 1024.4 | ||||
| 38 | 40 | 1112.2 | 24 | 38 | ||
More scales
Instruments
Guitars
The first 41edo guitar was probably this one, built by Erv Wilson in the 1960's:

Note the new bridge, several inches below the original bridge. The new bridge increases the scale length and spreads the frets out, making the guitar more playable. Erv numbered the frets as seen here, with the 3-limit dorian scale in enlarged numbers.
Several more modern guitars:
-
Melle Weijters' 10-string guitar (Melleweijters.com)
-
41edo electric guitar, by Gregory Sanchez.
-
41edo classical guitar, by Ron Sword.
The Kite Guitar is a guitar fretting using every other step of 41edo, i.e. 41ed4 or "20½-edo". However, the interval between two adjacent open strings is always an odd number of 41-edosteps. Thus each string only covers half of 41edo, but the full edo can be found on every pair of adjacent strings. Kite-fretting makes 41edo about as playable as 19edo or 22edo, although there are certain trade-offs.

For more photos of Kite guitars, see Kite Guitar Photographs.
Metallophones

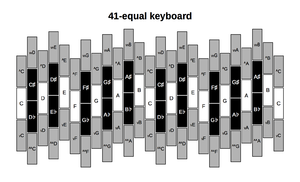
Keyboards
A possible 41edo keyboard design:
-
Tristan Bay's prototype TS41 MIDI keyboard, laid out in bosanquet with 41 keys per octave
See also 41-edo Keyboards for Linnstrument and Harpejji options, as well as DIY options.
Lumatone
See also 41-edo Keyboards for more Lumatone options.
Skip fretting
41edo as a Universal Tuning
41's claim to fame as a "universal tuning" is the fact that it approximates scales present in many important world music traditions, and thus is good for both combining and exploring cultural playstyles. It makes no claim to perfectly and faithfully represent the musical cultures listed, as doing so would require far more notes and small details than are present in 41. That being said, it has certain attributes that allow it to approximate common scales in these cultures with far more accuracy than most comparable EDOs.
Western
Due to 41edo's extremely accurate perfect fifth, it makes a good tuning for schismatic temperament and the 12-note MOS, which in turn is a good approximation of the standard 12edo scale, and when arranged as a Bbb-D gamut, approximates the 12-note roughly Pythagorean tuning known as Kirnberger I. This extends the Ptolemy Diatonic Scale (7 6 4 7 6 7 4), which 41 approximates excellently, by completing the circle of fifths with pure 3/2s. By using this system and occasionally substituting in alternate major seconds and sixths when necessary, it becomes quite reminiscent of (and can improve on) 12edo harmony. Additionally, the Pythagorean Pentatonic scale can be used for melodies overtop due to the strong quartal nature of the scale. The Pythagorean diatonic scale exists as an option as well, but use may be limited unless Gentle triads are ideal. An alternate option is approximating a Just Intonation scale such as the Asymmetric scale, a common option for a 5-limit JI scale, or Centaur, a 7-limit JI scale using "blue" or subminor intervals for the accidental notes. There exist other options for 5-limit JI scales, all of which have some reasonable approximation in 41 due to its relative excellence in the 5-limit.
Middle Eastern
While the Hemif[7] scale itself and MODMOSes related to it give the middle eastern sound well, 41 has other interesting properties that make it an ideal system for Arabic and Turkish music. It is considered a "Level 2 EDO" due to the fact that it has neutral seconds and thirds as well as submajor and supraminor ones added to a Pythagorean skeleton, with small semitones as minor seconds and major whole tones as major seconds. The submajor third is great for Turkish Rast, around Ozan Yarman’s ideal size, and is sharp enough to sound close to a 5/4, while the neutral third exists as half of a 3/2 and works well for Arabic Rast and some Persian scales. Additionally, a large apotome exists for the Hijaz maqam.
Indonesian
Gamelan music is mainly based on two scales, the older Slendro and newer Pelog, though these scales are expanded on extensively through octave stretching, extensions and combination of the scales, and more. Slendro is excellently approximated by the 8\41 generator. Pelog is approximated quite well also, this time by mavila temperament, using the "grave" fifth of 41 as the generator (23\41).
Indian
Carnatic music, which is normally based on a 22-note unequal scale, has found some use from 22edo as a good approximation, but 41 offers another option with Magic[22], which not only represents 22edo closely, but preserves accurate perfect fifths and the unequal quality of a more typical carnatic scale. Like any EDO system with an accurate 5-limit and essentially pure fifth, 41 can also approximate a system of Just Shrutis.
Japanese
Japanese classical music known as Gagaku is largely built around winds, strings, and percussion, and the melodies, like many Asian cultures, are built around Pythagorean pentatonic scales, alongside chromaticism with narrow semitones, which are well represented by Pythagorean limmas.
Blues
Due to its pure sounding major thirds and approximations of standard western harmony, 41 naturally is good for jazz and blues music, though a great strength of this system as opposed to many others is its excellent harmonic seventh, alongside MOS scales that supply them, Magic and Miracle in particular.
Coltrane changes can be represented with two Pythagorean major thirds and a pental one, or a temperament like Magic, whose MOSes are characterized by circles of major thirds, giving options for rotating major and minor triads within one scale. Similarly, the Whole Tone scale is represented by Baldy[6], with two pental major thirds and four Pythagorean. This scale can be extended to an 11-note MOS, including a single 4:5:7:9:11 chord and numerous subsets.
Superkleismic presents another option for this purpose, featuring circles of minor thirds, and generating harmonic sevenths with very low complexity.
Blue notes, rather than being considered inflections, can be notated as accidentals instead, such as the "blue third" which is represented by a neutral third, or any number of septimal intervals that are useful in a blues context.
Other
Georgian Polyphonic singing can be done in a 41edo context due to its excellent approximations of prime harmonics and neutral third, as well as Pythagorean seconds and sevenths. Asian musical traditions built around pentatonic scales can use both Pythagorean and Barbad[5].
Music
Modern renderings
- "Contrapunctus 4" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024)
- "Contrapunctus 11" from The Art of Fugue, BWV 1080 (1742–1749) – rendered by Claudi Meneghin (2024)
- Prelude in E Minor "The Great" – rendered by Claudi Meneghin (2023)
- Prelude in E Minor "The Little" – rendered by Claudi Meneghin (2024)
- Maple Leaf Rag (1899) – arranged for harpsichord and rendered by Claudi Meneghin (2024)
20th century
- Theme from Invisible Haircut (1990)
21st century
- FUZZ (2024)
- Subsidence vibe (2024)
- Notes of the Generation (2023) – an 8-piece album in 41et
- "Chaotic Witch #1" · "Party Cubes" · "Big Dreamer Pavilion" · "Lost Cyclops" · "Sky Tree" · "Long Night Ahead" · "Fractocraft" · "After the Generation"
- microtonal dance in 41edo (2023)
- Waltz in 41edo (2025)
- 41edo groove (2025)
- "Tetracotta" from XenRhythms (2024) – Spotify | Bandcamp | YouTube – in Tetracot[13], 41edo tuning
- "harmon" from TOTMC September to December 2024 (2024) – Spotify | Bandcamp | YouTube
- We Wish You A Gary Christmas (2024) – in gary, 41edo tuning
- Little Magical Object – in Magic[19], 41edo tuning
- Caftaphata (2024) – YouTube | SoundCloud – also partially in just intonation and 12edo
- Yxeni (2025) - YouTube
- Bohlen–Pierce Fugue for 3 Clarinets in 41EDO BPS9 sLsLsLsLs "Moll II/Pierce" (2023)
- 5-Part Bohlen–Pierce Fugue in 41EDO BPS9 sLsLsLssL "Harmonic" (2024)
- Chasing Dusk (2025)
- The Magic of Belief (2013) – in Magic[19], 41edo tuning
Kite Guitar recordings
- Evening Rondo
- Downminor Etude (midi demo)
- In the Know - Full album recorded using kite guitar & bass.
- Intervallic Prism (2020) – a 7-track album
- "Red" · "Orange" · "Yellow" · "Green" · "Blue" · "Indigo" · "Violet"
- 12-Bar-Blues on Kite Guitar – a simple 12-bar blues
- Fourthward Lang Syne – an arrangement of Auld Lang Syne
Kite Guitar videos
Kite Guitar scores
See also
- KiteGuitar.com for recordings, videos, etc.
- Magic22 as srutis describes a possible use of 41edo for indian music.
External links
- Tetracontamonophonic Scales for Guitar by Ron Sword
- Intervals, Scales and Chords in 41EDO by Cam Taylor – a work in progress using just intonation concepts and simplified Sagittal notation.
Notes
- ↑ Schismic Temperaments at x31eq.com, the website of Graham Breed
- ↑ Lattices with Decimal Notation at x31eq.com
- ↑ Ratios with more than 8 digits are presented by placeholders with informative hints