Duodene
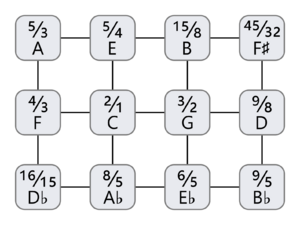
Duodene is a 12-note scale in just intonation, representing a natural approach to detempering standard 12edo, when considered as a 5-limit temperament. The scale was named by Alexander Ellis in an 1875 article[1] where he uses it to develop a theory of the chromatic scale in just intonation.
History
While Ellis formalized and named the system, it was first described by French engineer Salomon de Caus in 1615.[2] Marin Mersenne mentions it in his Harmonie universelle (Universal Harmony), and among piano tuners, the system is known as "Mersenne's spinet tuning No. 1."[3] The scale is also found in Euler's Tentamen novae theoriae musicae (Attempt at a New Theory of Music) from 1739.[4][5]
Musical properties
As a lattice structure, it consists of a chain of three perfect fifths (F – C – G – D) with just major thirds above and below each of these.[6] When arranged on a standard piano keyboard, the white keys of a duodene form a just diatonic scale, specifically Ptolemy's intense diatonic scale.
It can be constructed as a Fokker block with the syntonic comma (81/80) and the enharmonic diesis (128/125) as chromas. It is also an Euler-Fokker genus of [math]\displaystyle{ 675 = 3^3 \times 5^2 }[/math], meaning it comprises all divisors of 675, reduced by octave equivalence.
In Indian musical traditions, it is known as "Gandhar tuning."[citation needed]
As a detempering
Duodene can be tempered to several scales, which it can itself be understood as a detempering of.
Augmented diesis
If the augmented diesis is tempered out (as in 15edo), the MOS scale 3L 9s is obtained, where the large step represents 27/25 and 135/128, and the small step represents 16/15 and 25/24. This is one possible 12-note chromatic in augmented temperament.
Syntonic comma
If the syntonic comma is tempered out (as in 19edo), the MOS scale 7L 5s is obtained, where the large step represents 27/25 and 16/15, and the small step represents 135/128 and 25/24. This is the 12-note chromatic of meantone temperament.
If both chromas are tempered out, the result is 12-tone equal temperament (or an enfactoring, like 24edo).
Step pattern
Duodene is a tuning of the MV4 step pattern MnMsMnMMsLsM, which has 1 large step (27/25), 6 medium steps (16/15), 2 narrow steps (135/128), and 3 small steps (25/24). It can be represented in any edo which represents both the syntonic comma and the augmented diesis. The simplest tuning of this pattern is 29edo (s = 1, n = 2, M = 3, L = 4), but better tunings include 41edo and 53edo. In schismic temperament (which equates the augmented diesis and two syntonic commas), the sizes of the steps are equidistant.
Scala file
! duodene.scl ! Ellis's Duodene ! Fokblock([81/80, 128/125], [6,5]), genus [33355], Dwarf(⟨12 19 28]), syndie3, Gandhar tuning 12 ! 16/15 9/8 6/5 5/4 4/3 45/32 3/2 8/5 5/3 9/5 15/8 2/1
Music
- A different 12-tone subset of 34-equal (or thereabouts) on the harpsichord by Cam Taylor (2024)
- Duodene2 by Chris Vaisvil
See also
- Marveldene: the marvel tempered version of this scale.
References
- ↑ Alexander J. Ellis. On musical Duodenes, or the theory of constructing instruments with fixed tones in just or practically just intonation. in the Proceedings of the Royal Society of London, 1875, doi:10.1098/rspl.1874.0004
- ↑ Salomon de Caus, Les raisons des forces mouvantes avec diverses machines, Francfort, 1615, Book 3, Problem III.
Available online at: https://gallica.bnf.fr/ark:/12148/btv1b8626569p/f171.item - ↑ Marin Mersenne, Harmonie universelle, contenant la théorie et la pratique de la musique, Paris, 1636.
- ↑ Leonhard Euler, Tentamen novae theoriae musicae, St. Petersburg, 1739
- ↑ David J. Benson, Music: a mathematical offering, Cambridge University Press, 2006
- ↑ duodene in the Tonalsoft Encyclopedia of Microtonal Music Theory