Rodan
| Rodan |
245/243, 385/384, 441/440 (11-limit)
((2.3.5.7.11) 21-odd limit) 5.34 ¢
((2.3.5.7.11) 21-odd limit) 87 notes
Rodan is one of the notable extensions of the slendric temperament, which divides 3/2 into three equal intervals representing 8/7 (tempering out the gamelisma, 1029/1024), reaching the full 7-limit such that 17 of these generators stack to reach the interval class of the 5th harmonic. It tempers out 245/243, making it a sensamagic temperament, so that 5/3 is divided into two intervals of 9/7; and it tempers out 5120/5103, making it also a hemifamity temperament, so that 9/8 stacks thrice into 10/7.
Unlike mothra, which flattens the fifth to a meantone fifth, the fifth of rodan is slightly sharp of just, ranging from that of 41edo to that of 46edo (with 87edo being an essentially optimal tuning). As a result, the diatonic minor second is compressed, and the interval known as the quark, which represents 49/48, 64/63, and in rodan also 81/80, is even smaller than it is in tunings of slendric with a nearly just fifth. This entails that the mos scales of rodan cluster even more strongly around 5edo, although this can be thought of as an advantage in that it simplifies the conceptualization of rodan's inventory of intervals (see #As a detemperament of 5et). Rather than directly using mos scales, which are either extremely imbalanced or overly large, an approach to rodan may involve picking and choosing which intervals from each pentatonic category to keep in the scale.
As can be elucidated by S-expressions, rodan is very much an "opposed counterpart" to mothra: the basic equivalence of slendric tempers S7 (49/48) = S8 (64/63), and mothra proceeds to equate it to S6 (36/35) as well; meanwhile, rodan extends the equivalence in the opposite direction to add S9 (81/80) to it, making it one of the five rank-2 temperaments definable by equating three adjacent square superparticulars.
As for further extensions, slendric temperaments often find 55/32 at 4 generator steps (tempering out 385/384 and 441/440), giving new interpretations to the quark as 55/54 and 56/55; 55/32 is particularly accurate in the tuning subrange appropriate for rodan, and so harmonic 11 can easily be found at -13 generator steps. It is also worth mentioning that this equates the diatonic major third to 14/11, tempering out 896/891. A 2.3.7.11 subgroup version of rodan, known as radon, uses exclusively this mapping and forgoes interpreting the 5th harmonic.
Toward the 13-limit, the diatonic minor third (32/27) in hemifamity temperaments represents the square root of 7/5, for which 13/11 is a good interpretation (tempering out 352/351 and 847/845), which turns out to place harmonic 13 at -22 generator steps. Finally, 17/13 is a good interpretation of the slendric subfourth comprising two generators, otherwise equated to 21/16 (tempering out 273/272 and 833/832), and this places harmonic 17 at -20 generator steps. Thus proceeds the canonical extension of rodan out to the 17-limit.
See Gamelismic clan #Rodan for more information.
Interval chain
When speaking of interval categories, as an extension of slendric it is possible to use a system designed for slendric, where notes are inflected from the diatonic chain of fifths by means of the prefixes "super" and "sub", such that three of these inflections stack to a diatonic minor second. These "super" and "sub" prefixes are equivalent to "up" and "down" in the notation system, but can disambiguate from "up" and "down" symbols from ups and downs notation in the context of larger rodan edos that map this comma to multiple edosteps.
In the following table, odd harmonics and subharmonics 1–21 are in bold.
| # | Extended diatonic interval |
Cents* | Approximate ratios | |
|---|---|---|---|---|
| Ratios of the 11-limit | Ratios of the 17-limit | |||
| 0 | P1 | 0.00 | 1/1 | |
| 1 | SM2 | 234.46 | 8/7 | 39/34 |
| 2 | s4 | 468.92 | 21/16, 64/49 | 17/13 |
| 3 | P5 | 703.38 | 3/2 | |
| 4 | SM6 | 937.84 | 12/7, 55/32 | |
| 5 | s8 | 1172.30 | 55/28, 63/32, 96/49, 108/55, 160/81 | 51/26 |
| 6 | M2 | 206.76 | 9/8 | 44/39 |
| 7 | SM3 | 441.22 | 9/7, 35/27 | 22/17 |
| 8 | s5 | 675.68 | 40/27, 49/33, 72/49 | |
| 9 | M6 | 910.14 | 27/16, 56/33 | 22/13 |
| 10 | SM7 | 1144.59 | 27/14, 35/18, 64/33 | 33/17 |
| 11 | sM2 | 179.05 | 10/9 | |
| 12 | M3 | 413.51 | 14/11, 81/64 | 33/26 |
| 13 | SA4 | 647.97 | 16/11, 35/24 | |
| 14 | sM6 | 882.43 | 5/3 | |
| 15 | M7 | 1116.89 | 21/11, 40/21 | 98/51 |
| 16 | SA1 | 151.35 | 12/11, 35/32 | 56/51 |
| 17 | sM3 | 385.81 | 5/4 | 49/39, 64/51 |
| 18 | A4 | 620.27 | 10/7 | 49/34, 56/39 |
| 19 | SA5 | 854.73 | 18/11 | 28/17, 64/39 |
| 20 | sM7 | 1089.19 | 15/8 | 32/17, 49/26 |
| 21 | A1 | 123.65 | 15/14 | 14/13 |
| 22 | SA2 | 358.11 | 27/22, 60/49 | 16/13, 21/17 |
| 23 | sA4 | 592.57 | 45/32 | 24/17 |
| 24 | A5 | 827.03 | 45/28 | 21/13 |
| 25 | SA6 | 1061.49 | 50/27, 90/49 | 24/13 |
| 26 | sA1 | 95.95 | 35/33 | 18/17 |
| 27 | A2 | 330.41 | 40/33 | |
| 28 | SA3 | 564.87 | 25/18 | 18/13 |
| 29 | sA5 | 799.33 | 35/22, 100/63 | 27/17 |
| 30 | A6 | 1033.79 | 20/11 | |
| 31 | SA7 | 68.25 | 25/24 | 27/26 |
* In 11-limit CWE tuning, octave reduced
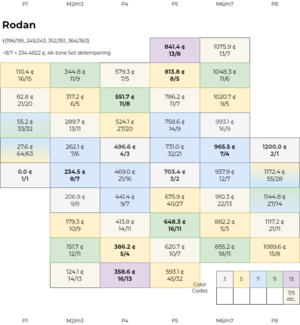
As a detemperament of 5et
Rodan is naturally a detemperament of the 5 equal temperament. The diagram on the right shows a 46-tone detempered scale, with a generator range of -22 to +23. 46 is the largest number of tones for a mos where intervals in the 5 categories do not overlap. Each category is divided into eight or nine qualities separated by 5 generator steps, which represent the syntonic comma.
Notice also the little interval between the largest of a category and the smallest of the next, which represents the differences between 16/15 and 14/13, between 11/9 and 16/13, between 7/5 and 45/32, between 13/8 and 18/11, and between 13/7 and 15/8. It spans 41 generator steps, so it vanishes in 41edo, but is tuned to the same size as the quark/syntonic comma in 46edo. 87edo tunes it to one half the size of the syntonic comma, which may be seen as a good compromise.
Chords
11-limit rodan contains essentially tempered chords of the commas 245/243, 385/384, 441/440, and 896/891. A list of 11-odd-limit dyadically consonant chords, both essentially tempered and essentially just, can be found at Chords of rodan.
Scales
Notation
A notation for rodan is listed in the notation guide for rank-2 pergens under pergen #8, (P8, P5/3). The generator is an upmajor second. The enharmonic unison is a triple-down minor second. Thus three ups equals a diatonic semitone, and three generators equals a perfect fifth. In rodan in particular, ^1 equals ~81/80 and ~64/63, and ^^1 equals ~33/32 and ~1053/1024.
| Ratio | Nominal | Example |
|---|---|---|
| 3/2 | Perfect fifth | C−G |
| 5/4 | Down major third | C−vE |
| 7/4 | Down minor seventh | C−vB♭ |
| 11/8 | Double-up fourth | C−^^F |
| 13/8 | Double-up minor sixth | C−^^A♭ |
Rodan's notation has much in common with that for 41edo and 46edo, since both edos map a minor second to three edosteps. It also resembles the notation for cassandra. All four notations notate the slendric tetrad (1–8/7–21/16–3/2) on C as C–^D–vF–G, and all four notations notate 5/4, 7/4, 11/8, and 13/8 as in the table above. But the notations diverge for other intervals, such as 11/10.
Tunings
Tuning spectrum
| EDO generator |
Unchanged interval (eigenmonzo) |
Generator (¢) | Comments |
|---|---|---|---|
| 8/7 | 231.1741 | Untempered tuning | |
| 17/13 | 232.2139 | ||
| 7\36 | 233.3333 | 36cfg val, lower bound of 7- and 9-odd-limit diamond monotone | |
| 3/2 | 233.9850 | 1/3-comma slendric | |
| 8\41 | 234.1463 | Lower bound of 11- through 17-odd-limit diamond monotone | |
| 22/17 | 234.1946 | ||
| 15/14 | 234.2592 | ||
| 10/7 | 234.3049 | 7- and 9-odd-limit minimax | |
| 33\169 | 234.3195 | 169fgg val | |
| 18/11 | 234.3470 | 11-odd-limit minimax | |
| 40/21 | 234.3689 | ||
| 25\128 | 234.3750 | 128g val | |
| 18/13 | 234.4065 | 13- and 15-odd-limit minimax | |
| 55/32 | 234.4079 | As SM6 | |
| 15/8 | 234.4134 | ||
| 12/11 | 234.4148 | ||
| 42\215 | 234.4186 | 215dgg val | |
| 15/11 | 234.4531 | ||
| 24/13 | 234.4571 | ||
| 15/13 | 234.4700 | ||
| 17\87 | 234.4828 | ||
| 5/4 | 234.4890 | 5-odd-limit minimax | |
| 20/11 | 234.4999 | ||
| 20/13 | 234.5073 | ||
| 16/11 | 234.5140 | ||
| 16/13 | 234.5215 | ||
| 22/13 | 234.5323 | ||
| 43\220 | 234.5455 | 220dg val | |
| 63/32 | 234.5472 | 2/5-comma slendric | |
| 18/17 | 234.5752 | 17-odd-limit minimax | |
| 30/17 | 234.5828 | ||
| 26\133 | 234.5865 | ||
| 5/3 | 234.5971 | ||
| 21/11 | 234.6309 | ||
| 20/17 | 234.6313 | ||
| 35\179 | 234.6369 | 179d val | |
| 24/17 | 234.6522 | ||
| 14/13 | 234.6809 | ||
| 32/17 | 234.7522 | ||
| 10/9 | 234.7640 | ||
| 9\46 | 234.7826 | Upper bound of 11- through 17-odd-limit diamond monotone | |
| 14/11 | 234.7923 | ||
| 28/17 | 234.9406 | ||
| 10\51 | 235.2941 | 51cf val | |
| 21/16 | 235.3905 | 1/2-comma slendric | |
| 1\5 | 240.0000 | 5f val, upper bound of 5- through 9-odd-limit diamond monotone |
* Besides the octave
Music
- Pianodactyl (archived 2010) – SoundCloud | detail | play – in Rodan[26], 87edo tuning