11-limit
The 11-limit consists of all justly tuned intervals whose numerators and denominators are both products of the primes 2, 3, 5, 7 and 11. The 11-limit is the 5th prime limit and is a superset of the 7-limit and a subset of the 13-limit. Some examples of 11-limit intervals are 14/11, 11/8, 27/22 and 99/98.
The 11-limit is a rank-5 system, and can be modeled in a 4-dimensional lattice, with the primes 3, 5, 7, and 11 represented by each dimension. The prime 2 does not appear in the typical 11-limit lattice because octave equivalence is presumed. If octave equivalence is not presumed, a fifth dimension is needed.
These things are contained by the 11-limit, but not the 7-limit:
- The 11-odd-limit;
- Mode 6 of the harmonic or subharmonic series.
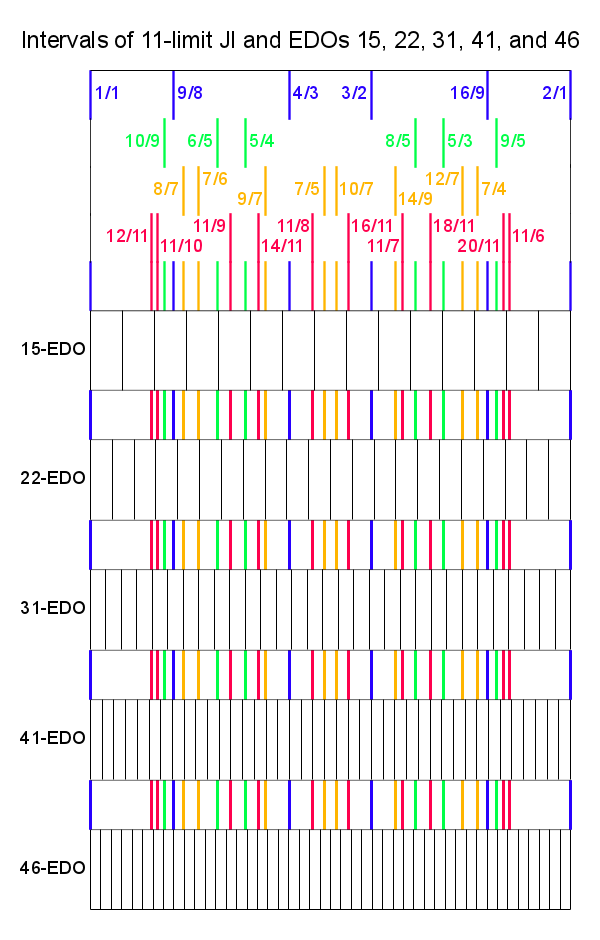
The 11-odd-limit consists of intervals whose numerators and denominators, when all factors of two have been removed, are less than or equal to 11. Reduced to an octave, these are the ratios 1/1, 12/11, 11/10, 10/9, 9/8, 8/7, 7/6, 6/5, 11/9, 5/4, 14/11, 9/7, 4/3, 11/8, 7/5, 10/7, 16/11, 3/2, 14/9, 11/7, 8/5, 18/11, 5/3, 12/7, 7/4, 16/9, 9/5, 20/11, 11/6, 2/1. In an 11-limit system, all the ratios of the 11 odd-limit can be treated as potential consonances.
While the 7-limit introduces subminor and supermajor intervals, which can sound like dramatic inflections of the familiar interval categories of 12edo, the 11-limit introduces neutral intervals, superfourths and subfifths, which fall in between major, minor and perfect interval categories and thus demand new distinctions. It is thus inescapably xenharmonic.
Edo approximation
Here is a list of edos which represent 11-limit intervals with better accuracy (monotonicity limit ≥ 11 and decreasing TE error): 12, 15, 19, 22, 27e, 31, 41, 53, 58, 72, 118, 130, 152, 224, 270, 342, 612 and so on. For a more comprehensive list, see Sequence of equal temperaments by error.
Here is a list of edos which tunes the 11-limit well relative to their size (TE relative error < 5%): 31, 41, 58, 72, 87, 118, 130, 152, 183, 190, 198, 212, 224, 239, 255, 270, 301, 311, 342, 369, 373, 400, 414, 422, 441, 453, 460, 463, 472, 494, 525, 552, 566, 581, 612 and so on.
- Note: wart notation is used to specify the val chosen for the edo. In the above list, "27e" means taking the second closest approximation of harmonic 11.
Intervals
11-odd-limit intervals
| Ratio | Color Name | Harmonic Solfege | |
|---|---|---|---|
| 12/11 | 1u2 | lu 2nd | fu-sol |
| 11/10 | 1og2 | logu 2nd | mi-fu |
| 10/9 | y2 | yo 2nd | re-mi |
| 9/8 | w2 | wa 2nd | do-re |
| 8/7 | r2 | ru 2nd | ta-do |
| 7/6 | z3 | zo 3rd | sol-ta |
| 6/5 | g3 | gu 3rd | mi-sol, ti-re |
| 11/9 | 1o3 | ilo 3rd | re-fu |
| 5/4 | y3 | yo 3rd | do-mi |
| 14/11 | 1uz4 | luzo 4th | fu-ta |
| 9/7 | r3 | ru 3rd | ta-re |
| 4/3 | w4 | wa 4th | do-fa |
| 11/8 | 1o4 | ilo 4th | do-fu |
| 7/5 | zg5 | zogu 5th | mi-ta |
| 10/7 | ry4 | ruyo 4th | ta-mi |
| 16/11 | 1u5 | lu 5th | fu-do |
| 3/2 | w5 | wa 5th | do-sol |
| 14/9 | z6 | zo 6th | re-ta |
| 11/7 | 1or5 | loru 5th | ta-fu |
| 8/5 | g6 | gu 6th | mi-do |
| 18/11 | 1u6 | lu 6th | fu-re |
| 5/3 | y6 | yo 6th | sol-mi |
| 12/7 | r6 | ru 6th | ta-sol |
| 7/4 | z7 | zo 7th | do-ta |
| 16/9 | w7 | wa 7th | re-do |
| 9/5 | g7 | gu 7th | mi-re |
| 20/11 | 1uy7 | luyo 7th | fu-mi |
| 11/6 | 1o7 | ilo 7th | sol-fu |
| 2/1 | w8 | wa 8ve | do-do |
Selected 15-odd-limit intervals
Here are all the 15-odd-limit intervals of 11:
| Ratio | Site (¢) | Color name | |
|---|---|---|---|
| 12/11 | 150.637 | 1u2 | lu 2nd |
| 11/10 | 165.004 | 1og2 | logu 2nd |
| 11/9 | 347.408 | 1o3 | ilo 3rd |
| 14/11 | 417.508 | 1uz4 | lu 4th |
| 15/11 | 536.951 | 1uy4 | luyo 4th |
| 11/8 | 551.318 | 1o4 | ilo 4th |
| 16/11 | 648.682 | 1u5 | lu 5th |
| 22/15 | 663.049 | 1og5 | logu 5th |
| 11/7 | 782.492 | 1or5 | loru 5th |
| 18/11 | 852.592 | 1u6 | lu 6th |
| 20/11 | 1034.996 | 1uy7 | luyo 7th |
| 11/6 | 1049.363 | 1o7 | ilo 7th |
Music
- Presence (2024)
- 11-limit singtervals (2012)
- Blue Canon (2013)
- 11-limit Canon on Elgar's Enigma Theme (2013)
- El Cant dels Ocells ("The Song of the Birds") – Catalan traditional, arranged by Claudi Meneghin (2013)
- A Keepsake Found After So Many Years (2021)
- Eros (2021)
- Music for Liminal Spaces (2021)
- Marshmallow Beatdown (2022)
- A Compendium of Things That Molecules Do (2022)