5L 2s

From Xenharmonic Wiki
Jump to navigation Jump to search
↖ 4L 1s↑ 5L 1s 6L 1s ↗
← 4L 2s5L 2s6L 2s →
↙ 4L 3s↓ 5L 3s 6L 3s ↘
 
┌╥╥╥┬╥╥┬┐
│║║║│║║││
│││││││││
└┴┴┴┴┴┴┴┘
Scale structure
Step pattern LLLsLLs
sLLsLLL
Equave 2/1 (1200.0¢)
Period 2/1 (1200.0¢)
Generator size
Bright 4\7 to 3\5 (685.7¢ to 720.0¢)
Dark 2\5 to 3\7 (480.0¢ to 514.3¢)
TAMNAMS information
Name diatonic
Prefix dia-
Abbrev. dia
Related MOS scales
Parent 2L 3s
Sister 2L 5s
Daughters 7L 5s, 5L 7s
Neutralized 3L 4s
2-Flought 12L 2s, 5L 9s
Equal tunings
Equalized (L:s = 1:1) 4\7 (685.7¢)
Supersoft (L:s = 4:3) 15\26 (692.3¢)
Soft (L:s = 3:2) 11\19 (694.7¢)
Semisoft (L:s = 5:3) 18\31 (696.8¢)
Basic (L:s = 2:1) 7\12 (700.0¢)
Semihard (L:s = 5:2) 17\29 (703.4¢)
Hard (L:s = 3:1) 10\17 (705.9¢)
Superhard (L:s = 4:1) 13\22 (709.1¢)
Collapsed (L:s = 1:0) 3\5 (720.0¢)
English Wikipedia has an article on:

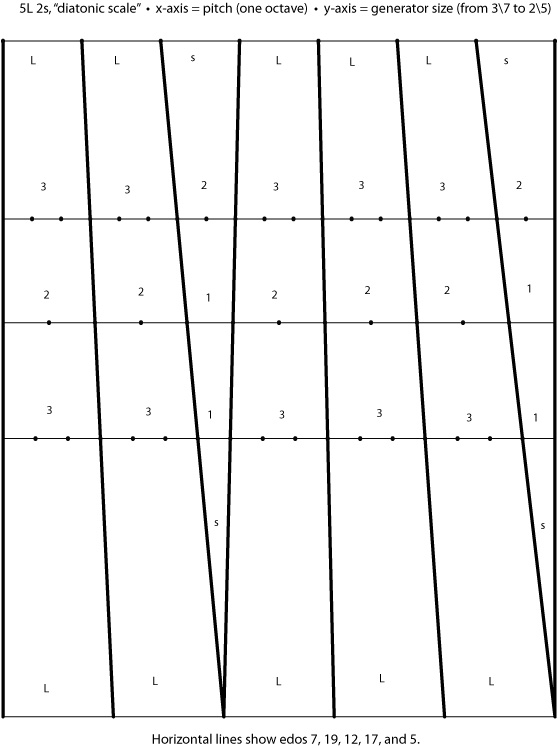
5L 2s, named diatonic in TAMNAMS, is a 2/1-equivalent (octave-equivalent) moment of symmetry scale containing 5 large steps and 2 small steps, repeating every octave. Generators that produce this scale range from 685.7¢ to 720¢, or from 480¢ to 514.3¢.

The familiar pattern of 5 whole steps and 2 half steps, commonly written as WWHWWWH for the major scale, takes on a generalized form of LLsLLLs, where the large and small steps – denoted as L's and s's – represent whole number step sizes, thus producing different edos. These step ratios affect the sizes of the diatonic scale's intervals and correspond to different tuning systems.

Among the most well-known forms of this scale are the Pythagorean diatonic scale, and scales produced by meantone systems (including 12edo).

Name

TAMNAMS suggests the temperament-agnostic name diatonic as the name of 5L 2s. The name commonly refers to a scale with 5 whole and 2 half steps, or 5 large and 2 small steps; see TAMNAMS/Appendix #On the term diatonic for more information.

Notation

This article assumes TAMNAMS for naming step ratios.

Intervals

Intervals are identical to that of standard notation. As such, the usual interval qualities of major/minor and augmented/perfect/diminished apply here.

Intervals of 5L 2s
Intervals Steps
subtended		 Range in cents
Generic Specific Abbrev.
0-diastep Perfect 0-diastep P0dias 0 0.0¢
1-diastep Minor 1-diastep m1dias s 0.0¢ to 171.4¢
Major 1-diastep M1dias L 171.4¢ to 240.0¢
2-diastep Minor 2-diastep m2dias L + s 240.0¢ to 342.9¢
Major 2-diastep M2dias 2L 342.9¢ to 480.0¢
3-diastep Perfect 3-diastep P3dias 2L + s 480.0¢ to 514.3¢
Augmented 3-diastep A3dias 3L 514.3¢ to 720.0¢
4-diastep Diminished 4-diastep d4dias 2L + 2s 480.0¢ to 685.7¢
Perfect 4-diastep P4dias 3L + s 685.7¢ to 720.0¢
5-diastep Minor 5-diastep m5dias 3L + 2s 720.0¢ to 857.1¢
Major 5-diastep M5dias 4L + s 857.1¢ to 960.0¢
6-diastep Minor 6-diastep m6dias 4L + 2s 960.0¢ to 1028.6¢
Major 6-diastep M6dias 5L + s 1028.6¢ to 1200.0¢
7-diastep Perfect 7-diastep P7dias 5L + 2s 1200.0¢

Note names

Note names are identical to that of standard notation. Thus, the basic gamut for 5L 2s is the following: C, C#/Db, D, D#/Eb, E, F, F#/Gb, G, G#/Ab, A, A#/Bb, B, C

Theory

Temperament interpretations

Main article: 5L 2s/Temperaments

5L 2s has several rank-2 temperament interpretations, such as:

  • Meantone, with generators around 696.2¢. This includes:
    • Flattone, with generators around 693.7¢.
  • Schismic, with generators around 702¢.
  • Parapyth, with generators around 704.7¢.
  • Archy, with generators around 709.3¢. This includes:
    • Supra, with generators around 707.2¢
    • Superpyth, with generators around 710.3¢
    • Ultrapyth, with generators around 713.7¢.

Warped diatonic scales

Because of most listeners’ familiarity with the 5L 2s diatonic scale, listeners may sometimes experience an effect like pareidolia, hearing 5L 2s even when it isn’t there.

A larger scale can be constructed so that it contains chains of 5L 2s, but then breaks the pattern, exploiting that pareidolic effect to surprise and disorient the listener. Scales which have this effect are called warped diatonic scales.

Tuning ranges

Icon-Todo.png Todo: Verify
Populate/verify tables

Simple tunings

17edo and 19edo are the smallest edos that offer a greater variety of pitches than 12edo. Note that any enharmonic equivalences that 12edo has no longer hold for either 17edo or 19edo, as shown in the table below.


Simple Tunings of 5L 2s
Scale degree Abbrev. Basic (2:1)
12edo 		Hard (3:1)
17edo 		Soft (3:2)
19edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\12 0.0 0\17 0.0 0\19 0.0 1/1
Minor 1-diadegree m1diad 1\12 100.0 1\17 70.6 2\19 126.3 22/21, 20/19, 18/17, 16/15, 15/14
Major 1-diadegree M1diad 2\12 200.0 3\17 211.8 3\19 189.5 10/9, 28/25, 9/8, 26/23, 17/15
Minor 2-diadegree m2diad 3\12 300.0 4\17 282.4 5\19 315.8 20/17, 13/11, 6/5
Major 2-diadegree M2diad 4\12 400.0 6\17 423.5 6\19 378.9 5/4, 24/19, 19/15, 14/11
Perfect 3-diadegree P3diad 5\12 500.0 7\17 494.1 8\19 505.3 4/3
Augmented 3-diadegree A3diad 6\12 600.0 9\17 635.3 9\19 568.4 7/5, 24/17, 17/12, 10/7
Diminished 4-diadegree d4diad 6\12 600.0 8\17 564.7 10\19 631.6 7/5, 24/17, 17/12, 10/7
Perfect 4-diadegree P4diad 7\12 700.0 10\17 705.9 11\19 694.7 3/2
Minor 5-diadegree m5diad 8\12 800.0 11\17 776.5 13\19 821.1 11/7, 30/19, 19/12, 8/5
Major 5-diadegree M5diad 9\12 900.0 13\17 917.6 14\19 884.2 5/3, 22/13, 17/10
Minor 6-diadegree m6diad 10\12 1000.0 14\17 988.2 16\19 1010.5 30/17, 23/13, 16/9, 25/14, 9/5
Major 6-diadegree M6diad 11\12 1100.0 16\17 1129.4 17\19 1073.7 28/15, 15/8, 17/9, 19/10, 21/11
Perfect 7-diadegree P7diad 12\12 1200.0 17\17 1200.0 19\19 1200.0 2/1

* Ratios shown are within the 30-integer limit. Automatic search may be inexact. Other interpretations are possible.

Ultrasoft tunings

Ultrasoft Tunings of 5L 2s
Scale degree Abbrev. 6:5
40edo 		5:4
33edo 		Supersoft (4:3)
26edo
Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\40 0.0 0\33 0.0 0\26 0.0
Minor 1-diadegree m1diad 5\40 150.0 4\33 145.5 3\26 138.5
Major 1-diadegree M1diad 6\40 180.0 5\33 181.8 4\26 184.6
Minor 2-diadegree m2diad 11\40 330.0 9\33 327.3 7\26 323.1
Major 2-diadegree M2diad 12\40 360.0 10\33 363.6 8\26 369.2
Perfect 3-diadegree P3diad 17\40 510.0 14\33 509.1 11\26 507.7
Augmented 3-diadegree A3diad 18\40 540.0 15\33 545.5 12\26 553.8
Diminished 4-diadegree d4diad 22\40 660.0 18\33 654.5 14\26 646.2
Perfect 4-diadegree P4diad 23\40 690.0 19\33 690.9 15\26 692.3
Minor 5-diadegree m5diad 28\40 840.0 23\33 836.4 18\26 830.8
Major 5-diadegree M5diad 29\40 870.0 24\33 872.7 19\26 876.9
Minor 6-diadegree m6diad 34\40 1020.0 28\33 1018.2 22\26 1015.4
Major 6-diadegree M6diad 35\40 1050.0 29\33 1054.5 23\26 1061.5
Perfect 7-diadegree P7diad 40\40 1200.0 33\33 1200.0 26\26 1200.0


Parasoft tunings

See also: Flattone

Parasoft diatonic tunings (4:3 to 3:2) correspond to flattone temperaments, characterized by flattened perfect 5ths (3/2, flat of 702¢) to produce major 3rds that are flatter than 5/4 (386¢).

Edos include 19edo, 26edo, 45edo, and 64edo.

Parasoft Tunings of 5L 2s
Scale degree Abbrev. Supersoft (4:3)
26edo 		7:5
45edo 		10:7
64edo 		Soft (3:2)
19edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\26 0.0 0\45 0.0 0\64 0.0 0\19 0.0 1/1
Minor 1-diadegree m1diad 3\26 138.5 5\45 133.3 7\64 131.2 2\19 126.3 14/13, 13/12
Major 1-diadegree M1diad 4\26 184.6 7\45 186.7 10\64 187.5 3\19 189.5 10/9, 9/8
Minor 2-diadegree m2diad 7\26 323.1 12\45 320.0 17\64 318.8 5\19 315.8 6/5
Major 2-diadegree M2diad 8\26 369.2 14\45 373.3 20\64 375.0 6\19 378.9 16/13, 26/21, 5/4
Perfect 3-diadegree P3diad 11\26 507.7 19\45 506.7 27\64 506.2 8\19 505.3 4/3
Augmented 3-diadegree A3diad 12\26 553.8 21\45 560.0 30\64 562.5 9\19 568.4 18/13
Diminished 4-diadegree d4diad 14\26 646.2 24\45 640.0 34\64 637.5 10\19 631.6 13/9
Perfect 4-diadegree P4diad 15\26 692.3 26\45 693.3 37\64 693.8 11\19 694.7 3/2
Minor 5-diadegree m5diad 18\26 830.8 31\45 826.7 44\64 825.0 13\19 821.1 8/5, 21/13, 13/8
Major 5-diadegree M5diad 19\26 876.9 33\45 880.0 47\64 881.2 14\19 884.2 5/3
Minor 6-diadegree m6diad 22\26 1015.4 38\45 1013.3 54\64 1012.5 16\19 1010.5 16/9, 9/5
Major 6-diadegree M6diad 23\26 1061.5 40\45 1066.7 57\64 1068.8 17\19 1073.7 24/13, 13/7
Perfect 7-diadegree P7diad 26\26 1200.0 45\45 1200.0 64\64 1200.0 19\19 1200.0 2/1

* Ratios shown are within the 2.3.5.7.13 subgroup. Automatic search may be inexact. Other interpretations are possible.

Hyposoft tunings

See also: Meantone

Hyposoft diatonic tunings (3:2 to 2:1) correspond to meantone temperaments, characterized by flattened perfect 5ths (flat of 702¢) to produce diatonic major 3rds that approximate 5/4 (386¢).

Edos include 19edo, 31edo, 43edo, and 50edo.

Hyposoft Tunings of 5L 2s
Scale degree Abbrev. Soft (3:2)
19edo 		8:5
50edo 		Semisoft (5:3)
31edo 		7:4
43edo 		Basic (2:1)
12edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\19 0.0 0\50 0.0 0\31 0.0 0\43 0.0 0\12 0.0 1/1
Minor 1-diadegree m1diad 2\19 126.3 5\50 120.0 3\31 116.1 4\43 111.6 1\12 100.0 16/15
Major 1-diadegree M1diad 3\19 189.5 8\50 192.0 5\31 193.5 7\43 195.3 2\12 200.0 10/9, 9/8
Minor 2-diadegree m2diad 5\19 315.8 13\50 312.0 8\31 309.7 11\43 307.0 3\12 300.0 6/5
Major 2-diadegree M2diad 6\19 378.9 16\50 384.0 10\31 387.1 14\43 390.7 4\12 400.0 5/4
Perfect 3-diadegree P3diad 8\19 505.3 21\50 504.0 13\31 503.2 18\43 502.3 5\12 500.0 4/3
Augmented 3-diadegree A3diad 9\19 568.4 24\50 576.0 15\31 580.6 21\43 586.0 6\12 600.0 25/18
Diminished 4-diadegree d4diad 10\19 631.6 26\50 624.0 16\31 619.4 22\43 614.0 6\12 600.0 36/25
Perfect 4-diadegree P4diad 11\19 694.7 29\50 696.0 18\31 696.8 25\43 697.7 7\12 700.0 3/2
Minor 5-diadegree m5diad 13\19 821.1 34\50 816.0 21\31 812.9 29\43 809.3 8\12 800.0 8/5
Major 5-diadegree M5diad 14\19 884.2 37\50 888.0 23\31 890.3 32\43 893.0 9\12 900.0 5/3
Minor 6-diadegree m6diad 16\19 1010.5 42\50 1008.0 26\31 1006.5 36\43 1004.7 10\12 1000.0 16/9, 9/5
Major 6-diadegree M6diad 17\19 1073.7 45\50 1080.0 28\31 1083.9 39\43 1088.4 11\12 1100.0 15/8
Perfect 7-diadegree P7diad 19\19 1200.0 50\50 1200.0 31\31 1200.0 43\43 1200.0 12\12 1200.0 2/1

* Ratios shown are within the 2.3.5 subgroup. Automatic search may be inexact. Other interpretations are possible.

Hypohard tunings

See also: Pythagorean tuning and schismatic temperament

The range of hypohard tunings can be divided into a minihard range (2:1 to 5:2) and quasihard range (5:2 to 3:1).

Hypohard Tunings of 5L 2s
Scale degree Abbrev. Basic (2:1)
12edo 		Semihard (5:2)
29edo 		Hard (3:1)
17edo
Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\12 0.0 0\29 0.0 0\17 0.0
Minor 1-diadegree m1diad 1\12 100.0 2\29 82.8 1\17 70.6
Major 1-diadegree M1diad 2\12 200.0 5\29 206.9 3\17 211.8
Minor 2-diadegree m2diad 3\12 300.0 7\29 289.7 4\17 282.4
Major 2-diadegree M2diad 4\12 400.0 10\29 413.8 6\17 423.5
Perfect 3-diadegree P3diad 5\12 500.0 12\29 496.6 7\17 494.1
Augmented 3-diadegree A3diad 6\12 600.0 15\29 620.7 9\17 635.3
Diminished 4-diadegree d4diad 6\12 600.0 14\29 579.3 8\17 564.7
Perfect 4-diadegree P4diad 7\12 700.0 17\29 703.4 10\17 705.9
Minor 5-diadegree m5diad 8\12 800.0 19\29 786.2 11\17 776.5
Major 5-diadegree M5diad 9\12 900.0 22\29 910.3 13\17 917.6
Minor 6-diadegree m6diad 10\12 1000.0 24\29 993.1 14\17 988.2
Major 6-diadegree M6diad 11\12 1100.0 27\29 1117.2 16\17 1129.4
Perfect 7-diadegree P7diad 12\12 1200.0 29\29 1200.0 17\17 1200.0


Minihard tunings

Minihard diatonic tunings correspond to Pythagorean tuning and schismatic temperament, characterized by having a perfect 5th that is as close to just (701.96¢) as possible, resulting in a major 3rd of 81/64 (407¢).

Edos include 41edo and 53edo.

Minihard Tunings of 5L 2s
Scale degree Abbrev. Basic (2:1)
12edo 		9:4
53edo 		7:3
41edo 		Semihard (5:2)
29edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\12 0.0 0\53 0.0 0\41 0.0 0\29 0.0 1/1
Minor 1-diadegree m1diad 1\12 100.0 4\53 90.6 3\41 87.8 2\29 82.8 256/243
Major 1-diadegree M1diad 2\12 200.0 9\53 203.8 7\41 204.9 5\29 206.9 9/8
Minor 2-diadegree m2diad 3\12 300.0 13\53 294.3 10\41 292.7 7\29 289.7 32/27
Major 2-diadegree M2diad 4\12 400.0 18\53 407.5 14\41 409.8 10\29 413.8 81/64
Perfect 3-diadegree P3diad 5\12 500.0 22\53 498.1 17\41 497.6 12\29 496.6 4/3
Augmented 3-diadegree A3diad 6\12 600.0 27\53 611.3 21\41 614.6 15\29 620.7 729/512
Diminished 4-diadegree d4diad 6\12 600.0 26\53 588.7 20\41 585.4 14\29 579.3 1024/729
Perfect 4-diadegree P4diad 7\12 700.0 31\53 701.9 24\41 702.4 17\29 703.4 3/2
Minor 5-diadegree m5diad 8\12 800.0 35\53 792.5 27\41 790.2 19\29 786.2 128/81
Major 5-diadegree M5diad 9\12 900.0 40\53 905.7 31\41 907.3 22\29 910.3 27/16
Minor 6-diadegree m6diad 10\12 1000.0 44\53 996.2 34\41 995.1 24\29 993.1 16/9
Major 6-diadegree M6diad 11\12 1100.0 49\53 1109.4 38\41 1112.2 27\29 1117.2 243/128
Perfect 7-diadegree P7diad 12\12 1200.0 53\53 1200.0 41\41 1200.0 29\29 1200.0 2/1

* Ratios shown are within the 3-prime limit. Automatic search may be inexact. Other interpretations are possible.

Quasihard tunings

Quasihard diatonic tunings correspond to "neogothic" or "parapyth" systems whose perfect 5th is slightly sharper than just, resulting in major 3rds that are sharper than 81/64 and minor 3rds that are slightly flat of 32/27 (294¢).

Edos include 17edo, 29edo, and 46edo. 17edo is considered to be on the sharper end of the neogothic spectrum, with a major 3rd that is more discordant than flatter neogothic tunings.

Quasihard Tunings of 5L 2s
Scale degree Abbrev. Semihard (5:2)
29edo 		8:3
46edo 		Hard (3:1)
17edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\29 0.0 0\46 0.0 0\17 0.0 1/1
Minor 1-diadegree m1diad 2\29 82.8 3\46 78.3 1\17 70.6 22/21
Major 1-diadegree M1diad 5\29 206.9 8\46 208.7 3\17 211.8 9/8
Minor 2-diadegree m2diad 7\29 289.7 11\46 287.0 4\17 282.4 13/11
Major 2-diadegree M2diad 10\29 413.8 16\46 417.4 6\17 423.5 14/11
Perfect 3-diadegree P3diad 12\29 496.6 19\46 495.7 7\17 494.1 4/3
Augmented 3-diadegree A3diad 15\29 620.7 24\46 626.1 9\17 635.3 13/9
Diminished 4-diadegree d4diad 14\29 579.3 22\46 573.9 8\17 564.7 18/13
Perfect 4-diadegree P4diad 17\29 703.4 27\46 704.3 10\17 705.9 3/2
Minor 5-diadegree m5diad 19\29 786.2 30\46 782.6 11\17 776.5 11/7
Major 5-diadegree M5diad 22\29 910.3 35\46 913.0 13\17 917.6 22/13
Minor 6-diadegree m6diad 24\29 993.1 38\46 991.3 14\17 988.2 16/9
Major 6-diadegree M6diad 27\29 1117.2 43\46 1121.7 16\17 1129.4 21/11
Perfect 7-diadegree P7diad 29\29 1200.0 46\46 1200.0 17\17 1200.0 2/1

* Ratios shown are within the 2.3.7.11.13 subgroup. Automatic search may be inexact. Other interpretations are possible.

Parahard and ultrahard tunings

See also: Archy

Parahard (3:1 to 4:1) and ultrahard (4:1 to 1:0) diatonic tunings correspond to archy systems, with perfect 5ths that are significantly sharper than than 702¢.

Edos include 17edo, 22edo, 27edo, and 32edo, among others.

Hard Tunings of 5L 2s
Scale degree Abbrev. Hard (3:1)
17edo 		Superhard (4:1)
22edo 		5:1
27edo 		6:1
32edo 		Approx. ratios*
Steps ¢ Steps ¢ Steps ¢ Steps ¢
Perfect 0-diadegree P0diad 0\17 0.0 0\22 0.0 0\27 0.0 0\32 0.0 1/1
Minor 1-diadegree m1diad 1\17 70.6 1\22 54.5 1\27 44.4 1\32 37.5 28/27
Major 1-diadegree M1diad 3\17 211.8 4\22 218.2 5\27 222.2 6\32 225.0 8/7
Minor 2-diadegree m2diad 4\17 282.4 5\22 272.7 6\27 266.7 7\32 262.5 7/6
Major 2-diadegree M2diad 6\17 423.5 8\22 436.4 10\27 444.4 12\32 450.0 9/7
Perfect 3-diadegree P3diad 7\17 494.1 9\22 490.9 11\27 488.9 13\32 487.5 4/3
Augmented 3-diadegree A3diad 9\17 635.3 12\22 654.5 15\27 666.7 18\32 675.0 72/49
Diminished 4-diadegree d4diad 8\17 564.7 10\22 545.5 12\27 533.3 14\32 525.0 49/36
Perfect 4-diadegree P4diad 10\17 705.9 13\22 709.1 16\27 711.1 19\32 712.5 3/2
Minor 5-diadegree m5diad 11\17 776.5 14\22 763.6 17\27 755.6 20\32 750.0 14/9
Major 5-diadegree M5diad 13\17 917.6 17\22 927.3 21\27 933.3 25\32 937.5 12/7
Minor 6-diadegree m6diad 14\17 988.2 18\22 981.8 22\27 977.8 26\32 975.0 7/4
Major 6-diadegree M6diad 16\17 1129.4 21\22 1145.5 26\27 1155.6 31\32 1162.5 27/14
Perfect 7-diadegree P7diad 17\17 1200.0 22\22 1200.0 27\27 1200.0 32\32 1200.0 2/1

* Ratios shown are within the 2.3.7 subgroup. Automatic search may be inexact. Other interpretations are possible.

Modes

Scale degrees of the modes of 5L 2s 
UDP Cyclic
Order		 Step
Pattern		 Scale Degree (diadegree)
0 1 2 3 4 5 6 7
6|0 1 LLLsLLs Perf. Maj. Maj. Aug. Perf. Maj. Maj. Perf.
5|1 5 LLsLLLs Perf. Maj. Maj. Perf. Perf. Maj. Maj. Perf.
4|2 2 LLsLLsL Perf. Maj. Maj. Perf. Perf. Maj. Min. Perf.
3|3 6 LsLLLsL Perf. Maj. Min. Perf. Perf. Maj. Min. Perf.
2|4 3 LsLLsLL Perf. Maj. Min. Perf. Perf. Min. Min. Perf.
1|5 7 sLLLsLL Perf. Min. Min. Perf. Perf. Min. Min. Perf.
0|6 4 sLLsLLL Perf. Min. Min. Perf. Dim. Min. Min. Perf.

Diatonic modes have standard names from classical music theory.

Modes of 5L 2s
UDP Cyclic
Order		 Step
Pattern		 Mode Names
6|0 1 LLLsLLs Lydian
5|1 5 LLsLLLs Ionian (major)
4|2 2 LLsLLsL Mixolydian
3|3 6 LsLLLsL Dorian
2|4 3 LsLLsLL Aeolian (minor)
1|5 7 sLLLsLL Phrygian
0|6 4 sLLsLLL Locrian

Scales

Subset and superset scales

5L 2s has a parent scale of 2L 3s, a pentatonic scale, meaning 2L 3s is a subset. 5L 2s also has two child scales, which are supersets of 5L 2s:

  • 7L 5s, a chromatic scale produced using soft-of-basic step ratios.
  • 5L 7s, a chromatic scale produced using hard-of-basic step ratios.

12edo, the equalized form of both 7L 5s and 5L 7s, is also a superset of 5L 2s.

MODMOS scales and muddles

Main articles: 5L 2s MODMOSes and 5L 2s Muddles

Scala files

Scale tree

Scale Tree and Tuning Spectrum of 5L 2s
Generator(edo) Cents Step Ratio Comments
Bright Dark L:s Hardness
4\7 685.714 514.286 1:1 1.000 Equalized 5L 2s
27\47 689.362 510.638 7:6 1.167
23\40 690.000 510.000 6:5 1.200
42\73 690.411 509.589 11:9 1.222
19\33 690.909 509.091 5:4 1.250
53\92 691.304 508.696 14:11 1.273
34\59 691.525 508.475 9:7 1.286
49\85 691.765 508.235 13:10 1.300
15\26 692.308 507.692 4:3 1.333 Supersoft 5L 2s
56\97 692.784 507.216 15:11 1.364
41\71 692.958 507.042 11:8 1.375
67\116 693.103 506.897 18:13 1.385
26\45 693.333 506.667 7:5 1.400 Flattone is in this region
63\109 693.578 506.422 17:12 1.417
37\64 693.750 506.250 10:7 1.429
48\83 693.976 506.024 13:9 1.444
11\19 694.737 505.263 3:2 1.500 Soft 5L 2s
51\88 695.455 504.545 14:9 1.556
40\69 695.652 504.348 11:7 1.571
69\119 695.798 504.202 19:12 1.583
29\50 696.000 504.000 8:5 1.600
76\131 696.183 503.817 21:13 1.615 Golden meantone (696.2145¢)
47\81 696.296 503.704 13:8 1.625
65\112 696.429 503.571 18:11 1.636
18\31 696.774 503.226 5:3 1.667 Semisoft 5L 2s
Meantone is in this region
61\105 697.143 502.857 17:10 1.700
43\74 697.297 502.703 12:7 1.714
68\117 697.436 502.564 19:11 1.727
25\43 697.674 502.326 7:4 1.750
57\98 697.959 502.041 16:9 1.778
32\55 698.182 501.818 9:5 1.800
39\67 698.507 501.493 11:6 1.833
7\12 700.000 500.000 2:1 2.000 Basic 5L 2s
Scales with tunings softer than this are proper
38\65 701.538 498.462 11:5 2.200
31\53 701.887 498.113 9:4 2.250 The generator closest to a just 3/2 for EDOs less than 200
55\94 702.128 497.872 16:7 2.286 Garibaldi / Cassandra
24\41 702.439 497.561 7:3 2.333
65\111 702.703 497.297 19:8 2.375
41\70 702.857 497.143 12:5 2.400
58\99 703.030 496.970 17:7 2.429
17\29 703.448 496.552 5:2 2.500 Semihard 5L 2s
61\104 703.846 496.154 18:7 2.571
44\75 704.000 496.000 13:5 2.600
71\121 704.132 495.868 21:8 2.625 Golden neogothic (704.0956¢)
27\46 704.348 495.652 8:3 2.667 Neogothic is in this region
64\109 704.587 495.413 19:7 2.714
37\63 704.762 495.238 11:4 2.750
47\80 705.000 495.000 14:5 2.800
10\17 705.882 494.118 3:1 3.000 Hard 5L 2s
43\73 706.849 493.151 13:4 3.250
33\56 707.143 492.857 10:3 3.333
56\95 707.368 492.632 17:5 3.400
23\39 707.692 492.308 7:2 3.500
59\100 708.000 492.000 18:5 3.600
36\61 708.197 491.803 11:3 3.667
49\83 708.434 491.566 15:4 3.750
13\22 709.091 490.909 4:1 4.000 Superhard 5L 2s
Archy is in this region
42\71 709.859 490.141 13:3 4.333
29\49 710.204 489.796 9:2 4.500
45\76 710.526 489.474 14:3 4.667
16\27 711.111 488.889 5:1 5.000
35\59 711.864 488.136 11:2 5.500
19\32 712.500 487.500 6:1 6.000
22\37 713.514 486.486 7:1 7.000
3\5 720.000 480.000 1:0 → ∞ Collapsed 5L 2s

Step ratio diagram

5L2s.jpg

See also

Retrieved from "https://en.xen.wiki/index.php?title=5L_2s&oldid=156103"