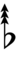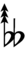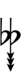70edo
| ← 69edo | 70edo | 71edo → |
70 equal divisions of the octave (abbreviated 70edo or 70ed2), also called 70-tone equal temperament (70tet) or 70 equal temperament (70et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 70 equal parts of about 17.1 ¢ each. Each step represents a frequency ratio of 21/70, or the 70th root of 2.
Theory
This tuning was singled out by William Stoney in his article "Theoretical Possibilities for Equally Tempered Systems" (in the book The Computer and Music) as one of the six best systems of size 72 or smaller, along with 72, 65, 58, 53, and 41. These other systems have had notice paid to them, but the same does not seem to be true of 70, which seems to have been ignored ever since, despite its excellent fifth, which is the 4th number in the convergent sequence to the silver ratio, following 29edo, 12edo & 5edo and preceding 169edo. The fifth 41\70 is the true center of the diatonic tuning spectrum, as it is the geometric mean of 3\5edo and 4\7edo.
The patent val for 70edo tempers out 2048/2025, making it a diaschismic system. An alternative mapping is 70c, with a flat rather than a sharp major third, tempering out 32805/32768. In the 7-limit, the patent val tempers out 126/125, 2430/2401 and 5120/5103, and provides the optimum patent val for the kumonga temperament. The 70c val tempers out 50/49, making it a tuning for doublewide even better than the optimal patent val. The 70cd val tempers out 225/224 and 3125/3087 instead. The alternative mapping begins to make more sense in the 11-limit and higher, where the patent val tempers out 99/98 and 121/120 in the 11-limit, 169/168 and 352/351 in the 13-limit, and 221/220 in the 17-limit. 70cd on the other hand, with flat 5 and 7, tempers out 100/99 and 245/242 in the 11-limit, 105/104 and 196/195 in the 13-limit, and 154/153 and 170/169 in the 17-limit. 70 also makes sense as a no-5 or -7 system, tempering out 131769/131072 in the 11-limit, 352/351 and 2197/2187 in the 13-limit, and 289/288 and 1089/1088 in the 17-limit.
The 17-limit 2*70 subgroup, on which 70 is tuned like 140edo, is 2.3.25.35.11.13.17.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | +0.90 | +7.97 | +8.32 | -2.75 | -0.53 | -2.10 | -6.08 | +6.01 |
| Relative (%) | +0.0 | +5.3 | +46.5 | +48.5 | -16.0 | -3.1 | -12.2 | -35.5 | +35.1 | |
| Steps (reduced) |
70 (0) |
111 (41) |
163 (23) |
197 (57) |
242 (32) |
259 (49) |
286 (6) |
297 (17) |
317 (37) | |
| Harmonic | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -1.01 | +3.54 | +5.80 | -0.49 | +2.77 | +3.06 | +0.78 | +3.69 | -2.60 |
| Relative (%) | -5.9 | +20.6 | +33.8 | -2.9 | +16.1 | +17.9 | +4.6 | +21.5 | -15.2 | |
| Steps (reduced) |
340 (60) |
347 (67) |
365 (15) |
375 (25) |
380 (30) |
389 (39) |
401 (51) |
412 (62) |
415 (65) | |
Subsets and supersets
Since 70 factors into 2 × 5 × 7, 70edo has subset edos 2, 5, 7, 10, 14, and 35. 140edo, which doubles it, provides good correction for its approximation to harmonics 5 and 7.
Intervals
| Steps | Cents | Approximate Ratios | Ups and Downs Notation |
|---|---|---|---|
| 0 | 0 | 1/1 | D |
| 1 | 17.143 | ^D, v4E♭ | |
| 2 | 34.286 | ^^D, v3E♭ | |
| 3 | 51.429 | 32/31, 33/32, 34/33 | ^3D, vvE♭ |
| 4 | 68.571 | 27/26 | ^4D, vE♭ |
| 5 | 85.714 | 21/20 | ^5D, E♭ |
| 6 | 102.857 | 17/16 | ^6D, v6E |
| 7 | 120 | 15/14, 29/27 | D♯, v5E |
| 8 | 137.143 | 13/12 | ^D♯, v4E |
| 9 | 154.286 | 12/11, 23/21 | ^^D♯, v3E |
| 10 | 171.429 | 32/29 | ^3D♯, vvE |
| 11 | 188.571 | 29/26 | ^4D♯, vE |
| 12 | 205.714 | 9/8 | E |
| 13 | 222.857 | 33/29 | ^E, v4F |
| 14 | 240 | 23/20, 31/27 | ^^E, v3F |
| 15 | 257.143 | 22/19, 36/31 | ^3E, vvF |
| 16 | 274.286 | 27/23, 34/29 | ^4E, vF |
| 17 | 291.429 | 13/11, 32/27 | F |
| 18 | 308.571 | 37/31 | ^F, v4G♭ |
| 19 | 325.714 | 29/24 | ^^F, v3G♭ |
| 20 | 342.857 | 28/23 | ^3F, vvG♭ |
| 21 | 360 | 16/13, 37/30 | ^4F, vG♭ |
| 22 | 377.143 | 36/29 | ^5F, G♭ |
| 23 | 394.286 | ^6F, v6G | |
| 24 | 411.429 | 33/26 | F♯, v5G |
| 25 | 428.571 | ^F♯, v4G | |
| 26 | 445.714 | 22/17, 31/24 | ^^F♯, v3G |
| 27 | 462.857 | 17/13, 30/23 | ^3F♯, vvG |
| 28 | 480 | 29/22, 37/28 | ^4F♯, vG |
| 29 | 497.143 | 4/3 | G |
| 30 | 514.286 | 31/23 | ^G, v4A♭ |
| 31 | 531.429 | ^^G, v3A♭ | |
| 32 | 548.571 | 11/8, 37/27 | ^3G, vvA♭ |
| 33 | 565.714 | 18/13 | ^4G, vA♭ |
| 34 | 582.857 | 7/5 | ^5G, A♭ |
| 35 | 600 | 17/12, 24/17 | ^6G, v6A |
| 36 | 617.143 | 10/7 | G♯, v5A |
| 37 | 634.286 | 13/9 | ^G♯, v4A |
| 38 | 651.429 | 16/11 | ^^G♯, v3A |
| 39 | 668.571 | ^3G♯, vvA | |
| 40 | 685.714 | ^4G♯, vA | |
| 41 | 702.857 | 3/2 | A |
| 42 | 720 | ^A, v4B♭ | |
| 43 | 737.143 | 23/15, 26/17 | ^^A, v3B♭ |
| 44 | 754.286 | 17/11 | ^3A, vvB♭ |
| 45 | 771.429 | ^4A, vB♭ | |
| 46 | 788.571 | ^5A, B♭ | |
| 47 | 805.714 | ^6A, v6B | |
| 48 | 822.857 | 29/18, 37/23 | A♯, v5B |
| 49 | 840 | 13/8 | ^A♯, v4B |
| 50 | 857.143 | 23/14 | ^^A♯, v3B |
| 51 | 874.286 | ^3A♯, vvB | |
| 52 | 891.429 | ^4A♯, vB | |
| 53 | 908.571 | 22/13, 27/16 | B |
| 54 | 925.714 | 29/17 | ^B, v4C |
| 55 | 942.857 | 19/11, 31/18 | ^^B, v3C |
| 56 | 960 | ^3B, vvC | |
| 57 | 977.143 | 37/21 | ^4B, vC |
| 58 | 994.286 | 16/9 | C |
| 59 | 1011.429 | ^C, v4D♭ | |
| 60 | 1028.571 | 29/16 | ^^C, v3D♭ |
| 61 | 1045.714 | 11/6 | ^3C, vvD♭ |
| 62 | 1062.857 | 24/13, 37/20 | ^4C, vD♭ |
| 63 | 1080 | 28/15 | ^5C, D♭ |
| 64 | 1097.143 | 32/17 | ^6C, v6D |
| 65 | 1114.286 | C♯, v5D | |
| 66 | 1131.429 | ^C♯, v4D | |
| 67 | 1148.571 | 31/16, 33/17 | ^^C♯, v3D |
| 68 | 1165.714 | ^3C♯, vvD | |
| 69 | 1182.857 | ^4C♯, vD | |
| 70 | 1200 | 2/1 | D |