17edo

← 16edo

17edo

18edo →

Prime factorization	17 (prime)
Step size	70.5882¢
Fifth	10\17 (705.882¢) (semiconvergent)
Semitones (A1:m2)	2:1 (141.2¢ : 70.59¢)
Consistency limit	3
Distinct consistency limit	3

17 equal divisions of the octave (17edo), or 17-tone equal temperament (17tet), 17 equal temperament (17et) when viewed from a regular temperament perspective, is the tuning system that divides the octave into 17 equal parts of about 70.6 ¢ each.

English Wikipedia has an article on:

17 equal temperament

Theory

17edo's perfect fifth is around 4 cents sharp of just, and around 6 cents sharp of 12edo's, lending itself to an expressive diatonic scale. Meanwhile, it approximates harmonics 7, 11, 13, and 23 to reasonable degrees, despite completely missing harmonic 5. Thus it can plausibly be treated as a 2.3.25.7.11.13.23 subgroup temperament, for which it is quite accurate (though the 7-limit ratios are generally not as well-represented as those of the other integers). Because these harmonics are all tempered sharp, it adapts well to octave shrinking; 27edt (a variant of 17edo in which the octaves are flattened by ~2.5 cents) is a good alternative. Another one is 44ed6.

Because the 5th harmonic is not well-approximated, using timbres with attenuated 5th harmonics (and its multiples) may reduce audible beating.

The standard major triad is quite dissonant as the major third is closer to 9/7 than the traditional 5/4. Instead, the tonic chords of 17edo could be considered to be the tetrad 6:7:8:9 and its utonal inversion (representing 14:16:18:21 as 64/63 is tempered out), the former of which is a subminor chord with added fourth, and the latter a supermajor chord with added second (resembling the mu chord of Steely Dan fame). These are realized in 17edo as 0-4-7-10 and 0-3-6-10, respectively. Both of these have distinct moods, and are stable and consonant, if somewhat more sophisticated than their classic 5-limit counterparts. To this group we could also add the 0-3-7-10 (which is a sus4 with added second, or sus2 with added fourth). These three chords comprise the three ways to divide the 17edo perfect fifth into two whole tones and one subminor third. Chromatic alterations of them also exist, for example, the 0-3-7-10 chord may be altered to 0-2-7-10 (which approximates 12:13:16:18) or 0-3-8-10 (which approximates 8:9:11:12). The 0-3-8-10 chord is impressive-sounding, resembling a sus4 but with even more tension; it resolves quite nicely to 0-3-6-10.

Another construction of septimal chords involves 4:7:12 and its inversion 7:12:21. These triads span a twelfth, realized in 17edo as 0-14-27 and 0-13-27, respectively. To this we may add 0-12-14-27, representing 8:13:14:24, or 0-13-15-27, representing 7:12:13:21.

Odd harmonics

Approximation of odd harmonics in 17edo

Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	absolute (¢)	+3.9	-33.4	+19.4	+7.9	+13.4	+6.5	-29.4	-34.4	-15.2	+23.3	+7.0
	relative (%)	+6	-47	+27	+11	+19	+9	-42	-49	-21	+33	+10
Steps (reduced)		27 (10)	39 (5)	48 (14)	54 (3)	59 (8)	63 (12)	66 (15)	69 (1)	72 (4)	75 (7)	77 (9)

Subsets and supersets

17edo is the seventh prime edo, following 13edo and coming before 19edo. 34edo, which doubles it, provides a good correction to the harmonic 5.

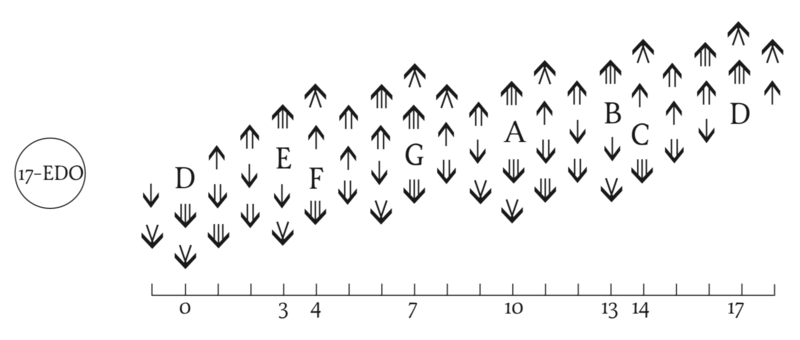
Intervals

See also: 17edo solfege

#	Cents	Approximate Ratios*	Circle-of-fifths Notation†		Ups and Downs Notation			3L 4s Notation
0	0.00	1/1	Unison	D	unison	P1	D	unison	D
1	70.59	22/21, 25/24, 26/25, 28/27, 33/32, 24/23	Minor 2nd (Semiaugmented 1sn)	Eb (D+)	up unison, minor 2nd	^1, m2	Eb	augmented 1sn	D#
2	141.18	13/12, 12/11, 14/13, 25/23	Augmented 1sn (Neutral 2nd)	D# (Ed)	augmented 1sn, mid 2nd	A1, ~2	vE	minor 2nd	Eb
3	211.76	9/8, 8/7, 28/25, 25/22, 26/23	Major 2nd	E	major 2nd	M2	E	major 2nd	E
4	282.35	13/11, 7/6	Minor 3rd	F	minor 3rd	m3	F	diminished 3rd	Fb
5	352.94	11/9, 16/13, 28/23	Diminished 4th (Neutral 3rd)	Gb (F+)	mid 3rd	~3	^F	perfect 3rd	F
6	423.53	32/25, 9/7, 14/11, 33/26, 23/18	Major 3rd (Semidiminished 4th)	F# (Gd)	major 3rd	M3	F#	augmented 3rd	F#
7	494.12	4/3, 21/16	Perfect 4th	G	perfect 4th	P4	G	minor 4th	G
8	564.71	11/8, 18/13, 32/23	Diminshed 5th (Semiaugmented 4th)	Ab (G+)	mid 4th, diminished 5th	~4, d5	^G, Ab	major 4th	G#
9	635.29	16/11, 13/9, 23/16	Augmented 4th (Semidiminished 5th)	G# (Ad)	augmented 4th, mid 5th	A4, ~5	G#, vA	minor 5th	Ab
10	705.88	3/2, 32/21	Perfect 5th	A	perfect 5th	P5	A	major 5th	A
11	776.47	25/16, 14/9, 11/7, 52/33, 36/23	Minor 6th (Semiaugmented 5th)	Bb (A+)	minor 6th	m6	Bb	diminished 6th	Bb
12	847.06	13/8, 18/11, 23/14	Augmented 5th (Neutral 6th)	A# (Bd)	mid 6th	~6	vB	perfect 6th	B
13	917.65	17/10, 22/13, 12/7	Major 6th	B	major 6th	M6	B	augmented 6th	B#
14	988.24	16/9, 7/4, 25/14, 44/25, 23/13	Minor 7th	C	minor 7th	m7	C	minor 7th	Cb
15	1058.82	11/6, 24/13, 13/7, 46/25	Diminished 8ve (Neutral 7th)	Db (C+)	mid 7th	~7	^C	major 7th	C
16	1129.41	21/11, 25/13, 48/25, 27/14, 64/33, 23/12	Major 7th (Semidiminished 8ve)	C# (Dd)	major 7th, down 8ve	M7, v8	C#	diminished 8ve	Db
17	1200.00	2/1	Octave	D	octave	P8	D	octave	D

* Ratios based on treating 17edo as a 2.3.7.11.13.23.25 subgroup temperament.

† Half-sharps and half-flats (denoted "+" and "d", respectively) can be used to alter the note by a single step, since sharps and flats each span two edosteps. Using half-sharps and half-flats may be preferable for compatibility with the ups-and-downs notation in 34edo, in which an up or down respectively constitute a quarter-sharp or quarter-flat.

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality	Color	Monzo Format	Examples
minor	zo	(a, b, 0, 1)	7/6, 7/4
	fourthward wa	(a, b), b < -1	32/27, 16/9
mid	ilo	(a, b, 0, 0, 1)	11/9, 11/6
	lu	(a, b, 0, 0, -1)	12/11, 18/11
major	fifthward wa	(a, b), b > 1	9/8, 27/16
	ru	(a, b, 0, -1)	9/7, 12/7

All 17edo chords can be named using ups and downs. Here are the zo, ilo and ru triads:

Color of the 3rd	JI Chord	Notes as Edosteps	Notes of C Chord	Written Name	Spoken Name
zo	6:7:9	0-4-10	C Eb G	Cm	C minor
ilo	18:22:27	0-5-10	C vE G	C~	C mid
ru	14:18:21	0-6-10	C E G	C	C major or C

Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

0-4-9 = C Eb vG = Cm(v5) = C minor down-five

0-5-9 = C vE vG = C~(v5) = C mid down-five

0-6-11 = C E ^G = C(^5) = C up-five

0-4-10-14 = C Eb G Bb = Cm7 = C minor seven

0-5-10-14 = C vE G Bb = C~,7 = C mid add seven

0-6-10-15 = C E G vB = C,~7 = C add mid-seven

0-5-10-15 = C vE G vB = C~7 = C mid-seven

For a more complete list, see Ups and downs notation #Chords and Chord Progressions.

Notation

Sagittal

From the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 17edo in the Revo flavor of Sagittal:

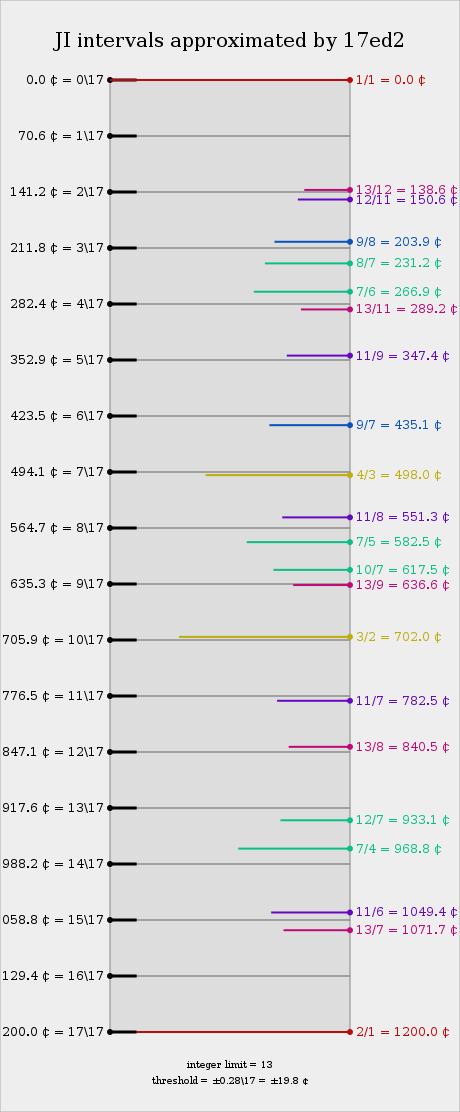
JI approximation

15-odd-limit interval mappings

The following table shows how 15-odd-limit intervals are represented in 17edo (ordered by absolute error). Prime harmonics are in bold; inconsistent intervals are in italic.

15-odd-limit intervals by direct approximation (even if inconsistent)

Interval, complement	Error (abs, ¢)	Error (rel, %)
18/13, 13/9	1.324	1.9
13/12, 24/13	2.604	3.7
4/3, 3/2	3.927	5.6
11/9, 18/11	5.533	7.8
14/11, 11/7	6.021	8.5
16/13, 13/8	6.531	9.3
13/11, 22/13	6.857	9.7
9/8, 16/9	7.855	11.1
12/11, 11/6	9.461	13.4
9/7, 14/9	11.555	16.4
14/13, 13/7	12.878	18.2
11/8, 16/11	13.388	19.0
7/6, 12/7	15.482	21.0
7/5, 10/7	17.806	25.2
8/7, 7/4	19.409	27.5
15/14, 28/15	21.734	30.8
11/10, 20/11	23.828	33.8
15/11, 22/15	27.755	39.3
10/9, 9/5	29.361	41.6
16/15, 15/8	29.445	41.7
13/10, 20/13	30.685	43.5
6/5, 5/3	33.288	47.2
5/4, 8/5	33.373	47.3
15/13, 26/15	34.612	49.0

15-odd-limit intervals by patent val mapping

Interval, complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
13/9, 18/13	1.324	1.9
13/12, 24/13	2.604	3.7
3/2, 4/3	3.927	5.6
11/9, 18/11	5.533	7.8
11/7, 14/11	6.021	8.5
13/8, 16/13	6.531	9.3
13/11, 22/13	6.857	9.7
9/8, 16/9	7.855	11.1
11/6, 12/11	9.461	13.4
9/7, 14/9	11.555	16.4
13/7, 14/13	12.878	18.2
11/8, 16/11	13.388	19.0
7/6, 12/7	15.482	21.9
7/4, 8/7	19.409	27.5
15/8, 16/15	29.445	41.7
5/4, 8/5	33.373	47.3
15/13, 26/15	35.976	51.0
5/3, 6/5	37.300	52.8
13/10, 20/13	39.904	56.5
9/5, 10/9	41.227	58.4
15/11, 22/15	42.833	60.7
11/10, 20/11	46.760	66.2
15/14, 28/15	48.855	69.2
7/5, 10/7	52.782	74.8

Selected 13-limit intervals

Tuning by ear

17edo is very close to a circle of seventeen 25/24 chromatic semitones: (25/24)^17 is only 1.43131 cents sharp of an octave. This means that if you can tune seventeen 25/24's accurately (by say, tuning 5/4 up, 3/2 down and 5/4 up, taking care to minimize the error at each step), you have a shot at approximating 17edo within melodic just noticeable difference.

Regular temperament properties

Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
				Absolute (¢)	Relative (%)
2.3	[27 -17⟩	[⟨17 27]]	-1.24	1.24	1.76
2.3.7	64/63, 17496/16807	[⟨17 27 48]]	-3.13	2.85	4.05
2.3.7.11	64/63, 99/98, 243/242	[⟨17 27 48 59]]	-3.31	2.49	3.54
2.3.7.11.13	64/63, 78/77, 99/98, 144/143	[⟨17 27 48 59 63]]	-3.00	2.31	3.28

17et is lower in relative error than any previous equal temperaments in the no-5 11- and 13-limit. The next equal temperaments doing better in these subgroups are 41 and 207, respectively.

Uniform maps

13-limit uniform maps between 16.5 and 17.5

Min. size	Max. size	Wart notation	Map
16.5000	16.5636	17bccdddeeefff	⟨17 26 38 46 57 61]
16.5636	16.5810	17bccdeeefff	⟨17 26 38 47 57 61]
16.5810	16.6196	17bdeeefff	⟨17 26 39 47 57 61]
16.6196	16.6212	17bdeeef	⟨17 26 39 47 57 62]
16.6212	16.7196	17bdef	⟨17 26 39 47 58 62]
16.7196	16.8899	17def	⟨17 27 39 47 58 62]
16.8899	16.9103	17de	⟨17 27 39 47 58 63]
16.9103	16.9198	17d	⟨17 27 39 47 59 63]
16.9198	17.0117	17	⟨17 27 39 48 59 63]
17.0117	17.1601	17c	⟨17 27 40 48 59 63]
17.1601	17.1994	17cff	⟨17 27 40 48 59 64]
17.1994	17.2760	17ceeff	⟨17 27 40 48 60 64]
17.2760	17.3506	17cddeeff	⟨17 27 40 49 60 64]
17.3506	17.4304	17bbcddeeff	⟨17 28 40 49 60 64]
17.4304	17.4424	17bbcddeeffff	⟨17 28 40 49 60 65]
17.4424	17.4884	17bbcccddeeffff	⟨17 28 41 49 60 65]
17.4884	17.5000	17bbcccddeeeeffff	⟨17 28 41 49 61 65]

Commas

17et tempers out the following commas. (Note: This assumes patent val ⟨17 27 39 48 59 63], cent values ​​rounded to 5 digits.)

Prime Limit	Ratio	Monzo	Cents	Color name	Name
3	(18 digits)	[27 -17⟩	66.765	Sasawa	17-comma
5	25/24	[-3 -1 2⟩	70.762	Yoyo	Dicot comma
5	32805/32768	[-15 8 1⟩	1.9537	Layo	Schisma
7	525/512	[-9 1 2 1⟩	43.408	Lazoyoyo	Avicennma
7	64/63	[6 -2 0 -1⟩	27.264	Ru	Septimal comma
7	245/243	[0 -5 1 2⟩	14.191	Zozoyo	Sensamagic comma
7	1728/1715	[6 3 -1 -3⟩	13.074	Triru-agu	Orwellisma
7	(12 digits)	[-6 -8 2 5⟩	1.1170	Quinzo-ayoyo	Wizma
11	99/98	[-1 2 0 -2 1⟩	17.576	Loruru	Mothwellsma
11	896/891	[7 -4 0 1 -1⟩	9.6880	Saluzo	Pentacircle
11	243/242	[-1 5 0 0 -2⟩	7.1391	Lulu	Rastma
11	385/384	[-7 -1 1 1 1⟩	4.5026	Lozoyo	Keenanisma
13	1352/1331	[3 0 0 0 -3 2⟩	27.101	Bithotrilu	Lovecraft comma
13	364/363	[2 -1 0 1 -2 1⟩	4.763	Tholuluzo	Gentle comma

Note that despite their relatively large size, the 17-comma, the avicennma and the chromatic semitone are all tempered out by the 13-limit patent val, as stated.

Rank-2 temperaments

• List of 17edo rank two temperaments by badness
• List of edo-distinct 17c rank two temperaments
• List of edo-distinct 17et rank two temperaments
• List of edo-distinct 17et no-fives rank two temperaments

Table of rank-2 temperaments by generator

Periods per 8ve	Generator	Cents	Associated Ratio	Temperament
1	2\17	141.18	13/12	Bleu / progression (17c)
1	3\17	211.76	8/7~9/8	Machine
1	4\17	282.35	13/11	Huxley[clarification needed] Lovecraft
1	5\17	352.94	11/9	Suhajira / neutrominant (17c) / beatles (17c) / dicotic (17) Hemif / mohamaq (17c) / salsa (17)
1	6\17	423.53	9/7	Skwares / squares (17c) / sentinel (17) / sidi (17)
1	7\17	494.12	4/3	Archy / supra / quasisuper (17c) / dominant (17c) / superpyth (17) / schism (17)
1	8\17	564.71	7/5	Lee / liese (17c) / pycnic (17) Progress (17c)

Scales

• Antipental blues
• Blues Peruvian 17edo
• Hydra
• 17edo neutral scale
• Otonal 17
• Scorp
• Screamapillar

MOS scales

Main article: MOS scales of 17edo

• diatonic (leapfrog/archy) 5L2s 3331331 (10\17, 1\1)
• maqamic 3L4s 3232322 (5\17, 1\1)
• maqamic 7L3s 2221221221 (5\17, 1\1)
• squares 3L5s 1141414 (6\17, 1\1)
• squares 3L8s 13113113 (6\17, 1\1)
• Pathological squares 3L11s 11211121112 (6\17, 1\1)
• lovecraft 4L5s 313131311 (4\17, 1\1)
• Pathological 1L 13s 4 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)
• Pathological 1L 14s 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)
• Pathological 2L 13s 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 (8\17, 1\1)
• Pathological 1L 15s 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (1\17, 1\1)

Well temperaments

• George Secor’s well temperament of this tuning
• Nicolai's 17-note Well Temperament
• Flora's 17-note well temperament

Introductory materials

• SeventeenTheory, an introduction to 17edo theory, through the eyes of the SeventeenTonePianoProject.
• The 17-tone Puzzle by George Secor, another introduction into 17edo theory.
• 17edo tetrachords
• Proyect 17-Perú ^[forbidden]

Music

Main article: 17edo/Music

See also: Category:17edo tracks

YouTube playlist of 17edo pieces

YouTube videos tagged with 17edo

Compositions from the Seventeen Tone Piano Project

• seventeen-tone piano project phase I
• Seventeen-tone piano project phase II
• Seventeen-tone piano project phase III

Instruments

• Guitar Heptadecatonic from Peruvian - Charles Loli and Antonio Huamani ^[forbidden]

External image: http://sphotos.ak.fbcdn.net/hphotos-ak-snc4/hs883.snc4/71639_167001659983806_100000219181856_601995_1526184_n.jpg ^{[dead link]}

WARNING: MediaWiki doesn't have very good support for external images.

Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.

• Bass Heptadecatonic from Peruvian - Charles Loli and Antonio Huamani ^[forbidden]

External image: http://sphotos.ak.fbcdn.net/hphotos-ak-ash2/hs382.ash2/66019_167001006650538_100000219181856_601987_48585_n.jpg ^{[dead link]}

WARNING: MediaWiki doesn't have very good support for external images.

Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.

• 17 note per octave conversion from a "standard" Stratocaster copy - conversion by Brad Smith

See also

• Lumatone mapping for 17edo