SeventeenTheory

17-tone equal tuning has fifths very close to just-intonation (and 12-equal) fifths. Consequently we use the usual circle-of-fifths on a five-line-staff notation, with a twist of new enharmonic equivalents, caused by the accumulation of the difference in the size of the fifth. To figure out the enharmonic names of any closed circle of fifths, write out a portion of it, like:

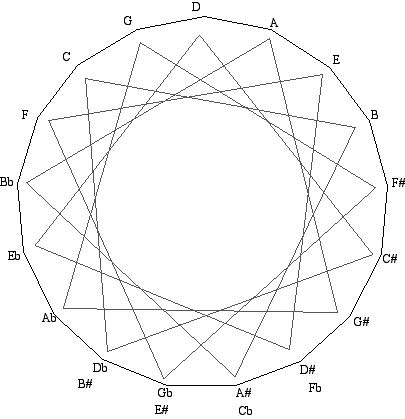
Cb Gb Db Ab Eb Bb F C G D A E B F# C# G# D# A# E#

and then wrap it into a circle of the desired size. If you do this with 17, you will notice that Cb = A#...that's how big the value of "flat/sharp" is in 17. The closer two notes are in the circle, the more familiar to us their harmonic function.

The lines across indicate five fourths = "minor second" = 1/17 of an octave. (We know this because 17's perfect fourth is 7/17 of an octave, and 7*5 modulo 17 = 1.)

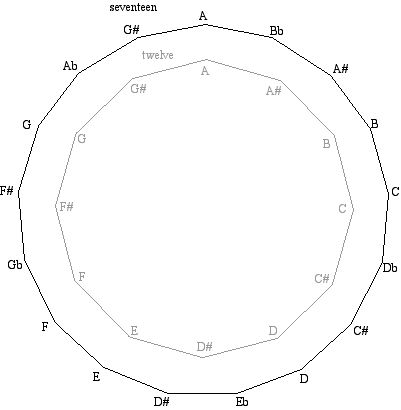
So if we re-wrap the circle according to these lines, we should get the 17 notes of the scale in ascending/descending order (I moved A to the top just because):

Note that C# is HIGHER than Db; note that none of the intervals save the octave/unison are exactly the same as in 12. Note that The "half step"/"minor second" in 17 is twice as small as the "augmented unison"/"sharp"/"flat." Two sharp/flats add up to a minor third. Two "neutral thirds" add up to a "perfect fifth." 17 shares this last property with the quartertone scale (24-EDO).

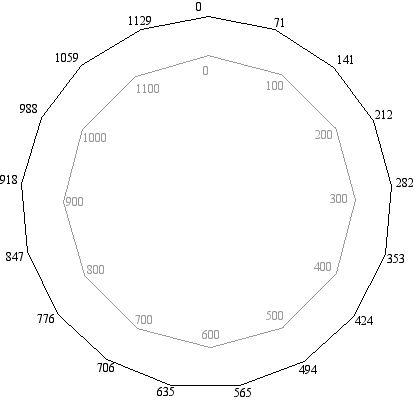
If the old notation is bothering you, here it is in cents (hundredths of a 12-equal half step):

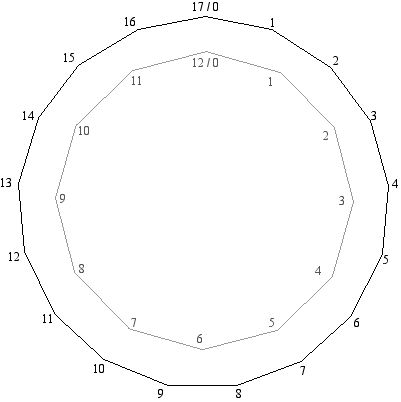
and in pitch/interval classes: