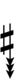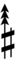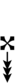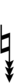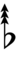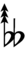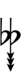68edo

From Xenharmonic Wiki
Jump to navigation Jump to search
← 67edo 68edo 69edo →
Prime factorization 22 × 17
Step size 17.6471 ¢ 
Fifth 40\68 (705.882 ¢) (→ 10\17)
Semitones (A1:m2) 8:4 (141.2 ¢ : 70.59 ¢)
Consistency limit 9
Distinct consistency limit 9

68 equal divisions of the octave (abbreviated 68edo or 68ed2), also called 68-tone equal temperament (68tet) or 68 equal temperament (68et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 68 equal parts of about 17.6 ¢ each. Each step represents a frequency ratio of 21/68, or the 68th root of 2.

Theory

68edo's step is half of the step size of 34edo, which does well in the 5-limit but not so well in the 7-limit, and one quarter the size of 17edo, which does well in the 3-limit, but not so well in the 5-limit. The luck continues: 68 is a strong 7-limit system, but does not do as well in the 11-limit; though it's certainly usable for that purpose, it does not represent the 11-limit diamond consistently. However, 68edo maps many higher primes better than it does 11 (specifically 13 and 23 inherited from 17edo, 17 inherited from 34edo, and 19 and 31 new to 68edo), notably being consistent in the entire no-11s 25-odd limit add-31. It achieves this by having a consistent sharp tendency among all primes up to 31, save 11 and 29. Therefore, a slight octave compression, such as in 158ed5 or 191ed7, can improve upon the accuracy of 68edo's harmonic series.

As a 7-limit system, 68et tempers out 2048/2025, 245/243, 4000/3969, 15625/15552, 3136/3125, 6144/6125, and 2401/2400. It supports octacot, shrutar, hemiwürschmidt, hemikleismic, clyde and neptune temperaments, and supplies the optimal patent val for 11-limit hemikleismic.

The 3rd degree of 68edo can be used as a generator for stretched 23edo, which also acts as the quartkeenlig temperament tempering out the quartisma, 385/384 and 6250/6237. It results in a 23edo scale with octaves stretched by 1 step of 68edo (octaves of 1217.65 ¢). It also works as a 22L 1s MOS of the quartkeenlig temperament.

The 5th degree of 68edo can be used as a generator for 88cET, while two steps almost perfectly approximate 50/49, allowing for the tempering out of 2/(50/49)34.

Prime harmonics

Approximation of prime harmonics in 68edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.00 +3.93 +1.92 +1.76 -4.26 +6.53 +0.93 +2.49 +7.02 -6.05 +2.02
Relative (%) +0.0 +22.3 +10.9 +10.0 -24.1 +37.0 +5.3 +14.1 +39.8 -34.3 +11.5
Steps
(reduced) 		68
(0) 		108
(40) 		158
(22) 		191
(55) 		235
(31) 		252
(48) 		278
(6) 		289
(17) 		308
(36) 		330
(58) 		337
(65)

Subsets and supersets

Since 68 factors into 22 × 17, 68edo has subset edos 2, 4, 17, and 34.

Intervals

Degrees Cents Approximate ratios
0 0.00 1/1
1 17.65 64/63, 126/125, 225/224
2 35.29 81/80, 49/48, 50/49
3 52.94 28/27, 36/35, 33/32
4 70.59 25/24, 22/21
5 88.24 21/20, 19/18, 20/19
6 105.88 16/15, 17/16, 18/17
7 123.53 15/14, 14/13
8 141.18 13/12
9 158.82 12/11, 11/10
10 176.47 10/9
11 194.12 28/25, 19/17
12 211.76 9/8
13 229.41 8/7
14 247.06 15/13
15 264.71 7/6
16 282.35 20/17
17 300.00 13/11, 19/16
18 317.65 6/5
19 335.29 11/9, 40/33, 17/14
20 352.94 16/13, 39/32
21 370.59 27/22, 26/21, 21/17
22 388.24 5/4
23 405.88 24/19, 19/15
24 423.53 14/11
25 441.18 9/7
26 458.82 13/10, 17/13
27 476.47 21/16
28 494.12 4/3
29 511.76 75/56
30 529.41 27/20, 19/14
31 547.06 11/8, 15/11
32 564.71 25/18, 18/13, 26/19
33 582.35 7/5
34 600.00 17/12, 24/17
35 617.65 10/7
36 635.29 36/25, 13/9, 19/13
37 652.94 16/11, 22/15
38 670.59 40/27, 28/19
39 688.24 112/75
40 705.88 3/2
41 723.53 32/21
42 741.18 16/13, 26/17
43 758.82 14/9
44 776.47 11/7
45 794.12 19/12, 30/19
46 811.76 8/5
47 829.41 44/27, 21/13, 34/21
48 847.06 13/8, 64/39
49 864.71 18/11, 33/20, 28/17
50 882.35 5/3
51 900.00 22/13, 32/19
52 917.65 17/10
53 935.29 12/7
54 952.94 26/15
55 970.59 7/4
56 988.24 16/9
57 1005.88 25/14, 34/19
58 1023.53 9/5
59 1041.18 11/6, 20/11
60 1058.82 24/13
61 1076.47 28/15, 13/7
62 1094.12 15/8, 32/17, 17/9
63 1111.76 40/21, 36/19, 19/10
64 1129.41 48/25, 21/11
65 1147.06 27/14, 35/18, 64/33
66 1164.71 160/81, 96/49, 49/25
67 1182.35 63/32, 125/64, 448/225
68 1200.00 2/1

Notation

Ups and downs notation

68edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Sharp symbol  
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 75-EDO.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/3227/26

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/3227/26

Evo-SZ flavor

Sagittal notationPeriodic table of EDOs with sagittal notation64/6381/8033/3227/26

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.

Approximation to JI

Interval mappings

The following tables show how 15-odd-limit intervals are represented in 68edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 68edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
7/5, 10/7 0.159 0.9
15/13, 26/15 0.682 3.9
13/9, 18/13 1.324 7.5
7/4, 8/7 1.762 10.0
5/4, 8/5 1.922 10.9
5/3, 6/5 2.006 11.4
7/6, 12/7 2.165 12.3
13/12, 24/13 2.604 14.8
3/2, 4/3 3.927 22.3
15/14, 28/15 4.087 23.2
11/8, 16/11 4.259 24.1
13/10, 20/13 4.610 26.1
13/7, 14/13 4.769 27.0
11/9, 18/11 5.533 31.4
15/8, 16/15 5.849 33.1
9/5, 10/9 5.933 33.6
11/7, 14/11 6.021 34.1
9/7, 14/9 6.092 34.5
11/10, 20/11 6.181 35.0
13/8, 16/13 6.531 37.0
13/11, 22/13 6.857 38.9
15/11, 22/15 7.539 42.7
9/8, 16/9 7.855 44.5
11/6, 12/11 8.186 46.4
15-odd-limit intervals in 68edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
7/5, 10/7 0.159 0.9
15/13, 26/15 0.682 3.9
13/9, 18/13 1.324 7.5
7/4, 8/7 1.762 10.0
5/4, 8/5 1.922 10.9
5/3, 6/5 2.006 11.4
7/6, 12/7 2.165 12.3
13/12, 24/13 2.604 14.8
3/2, 4/3 3.927 22.3
15/14, 28/15 4.087 23.2
11/8, 16/11 4.259 24.1
13/10, 20/13 4.610 26.1
13/7, 14/13 4.769 27.0
15/8, 16/15 5.849 33.1
9/5, 10/9 5.933 33.6
11/7, 14/11 6.021 34.1
9/7, 14/9 6.092 34.5
11/10, 20/11 6.181 35.0
13/8, 16/13 6.531 37.0
9/8, 16/9 7.855 44.5
11/6, 12/11 8.186 46.4
15/11, 22/15 10.108 57.3
13/11, 22/13 10.790 61.1
11/9, 18/11 12.114 68.6

Zeta peak index

Tuning Strength Octave (cents) Integer limit
ZPI Steps
per 8ve 		Step size
(cents) 		Height Integral Gap Size Stretch Consistent Distinct
Tempered Pure
354zpi 68.049306 17.634273 7.666604 6.147517 1.254592 17.034505 1199.130531 −0.869469 10 10

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3.5.7 245/243, 2048/2025, 2401/2400 [⟨68 108 158 191]] −0.983 0.915 5.19
2.3.5.7.11 121/120, 176/175, 245/243, 1375/1372 [⟨68 108 158 191 235]] −0.541 1.206 6.84
2.3.5.7.11.13 121/120, 176/175, 196/195, 245/243, 275/273 [⟨68 108 158 191 235 252]] −0.745 1.191 6.75
2.3.5.7.11.13.17 121/120, 136/135, 154/153, 176/175, 196/195, 275/273 [⟨68 108 158 191 235 252 278]] −0.671 1.118 6.34
2.3.5.7.11.13.17.19 121/120, 136/135, 154/153, 190/189, 176/175, 196/195, 275/273 [⟨68 108 158 191 235 252 278 289]] −0.661 1.046 5.93

Scales

See also: List of MOS scales in 68edo, 34edo #Scales, and 17edo #Scales.
  • Negative semitone: 14 14 -1 14 14 14 -1 (E is sharper than F, and B is sharper than C)
  • Deeptone[7]: 10 10 9 10 10 10 9
  • Inverse half octave: 4 4 7 4 4 4 4 7 4 4 7 4 4 4 4 7
  • Superpyth quarter octave: 3 3 1 3 3 3 1 3 3 1 3 3 3 1 3 3 1 3 3 3 1 3 3 1 3 3 3 1
  • Quartkeenlig[23] (Stretched 23edo): 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2

Music

The Mercury Tree
Retrieved from "https://en.xen.wiki/index.php?title=68edo&oldid=200444"