This page lists all moment of symmetry scales in 17edo.
Single-period MOS scales
Generators 9\17 and 8\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├────────┼───────┤
|
1L 1s
|
9, 8
|
9:8
|
| ├┼───────┼───────┤
|
2L 1s
|
8, 1
|
8:1
|
| ├┼┼──────┼┼──────┤
|
2L 3s
|
7, 1
|
7:1
|
| ├┼┼┼─────┼┼┼─────┤
|
2L 5s (antidiatonic)
|
6, 1
|
6:1
|
| ├┼┼┼┼────┼┼┼┼────┤
|
2L 7s (balzano)
|
5, 1
|
5:1
|
| ├┼┼┼┼┼───┼┼┼┼┼───┤
|
2L 9s
|
4, 1
|
4:1
|
| ├┼┼┼┼┼┼──┼┼┼┼┼┼──┤
|
2L 11s
|
3, 1
|
3:1
|
| ├┼┼┼┼┼┼┼─┼┼┼┼┼┼┼─┤
|
2L 13s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 10\17 and 7\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├─────────┼──────┤
|
1L 1s
|
10, 7
|
10:7
|
| ├──┼──────┼──────┤
|
2L 1s
|
7, 3
|
7:3
|
| ├──┼──┼───┼──┼───┤
|
2L 3s
|
4, 3
|
4:3
|
| ├──┼──┼──┼┼──┼──┼┤
|
5L 2s (diatonic)
|
3, 1
|
3:1
|
| ├─┼┼─┼┼─┼┼┼─┼┼─┼┼┤
|
5L 7s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 11\17 and 6\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├──────────┼─────┤
|
1L 1s
|
11, 6
|
11:6
|
| ├────┼─────┼─────┤
|
2L 1s
|
6, 5
|
6:5
|
| ├────┼────┼┼────┼┤
|
3L 2s
|
5, 1
|
5:1
|
| ├───┼┼───┼┼┼───┼┼┤
|
3L 5s (checkertonic)
|
4, 1
|
4:1
|
| ├──┼┼┼──┼┼┼┼──┼┼┼┤
|
3L 8s
|
3, 1
|
3:1
|
| ├─┼┼┼┼─┼┼┼┼┼─┼┼┼┼┤
|
3L 11s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 12\17 and 5\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├───────────┼────┤
|
1L 1s
|
12, 5
|
12:5
|
| ├──────┼────┼────┤
|
1L 2s
|
7, 5
|
7:5
|
| ├─┼────┼────┼────┤
|
3L 1s
|
5, 2
|
5:2
|
| ├─┼─┼──┼─┼──┼─┼──┤
|
3L 4s (mosh)
|
3, 2
|
3:2
|
| ├─┼─┼─┼┼─┼─┼┼─┼─┼┤
|
7L 3s (dicoid)
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 13\17 and 4\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├────────────┼───┤
|
1L 1s
|
13, 4
|
13:4
|
| ├────────┼───┼───┤
|
1L 2s
|
9, 4
|
9:4
|
| ├────┼───┼───┼───┤
|
1L 3s
|
5, 4
|
5:4
|
| ├┼───┼───┼───┼───┤
|
4L 1s
|
4, 1
|
4:1
|
| ├┼┼──┼┼──┼┼──┼┼──┤
|
4L 5s (gramitonic)
|
3, 1
|
3:1
|
| ├┼┼┼─┼┼┼─┼┼┼─┼┼┼─┤
|
4L 9s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 14\17 and 3\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├─────────────┼──┤
|
1L 1s
|
14, 3
|
14:3
|
| ├──────────┼──┼──┤
|
1L 2s
|
11, 3
|
11:3
|
| ├───────┼──┼──┼──┤
|
1L 3s
|
8, 3
|
8:3
|
| ├────┼──┼──┼──┼──┤
|
1L 4s
|
5, 3
|
5:3
|
| ├─┼──┼──┼──┼──┼──┤
|
5L 1s (machinoid)
|
3, 2
|
3:2
|
| ├─┼─┼┼─┼┼─┼┼─┼┼─┼┤
|
6L 5s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 15\17 and 2\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├──────────────┼─┤
|
1L 1s
|
15, 2
|
15:2
|
| ├────────────┼─┼─┤
|
1L 2s
|
13, 2
|
13:2
|
| ├──────────┼─┼─┼─┤
|
1L 3s
|
11, 2
|
11:2
|
| ├────────┼─┼─┼─┼─┤
|
1L 4s
|
9, 2
|
9:2
|
| ├──────┼─┼─┼─┼─┼─┤
|
1L 5s (antimachinoid)
|
7, 2
|
7:2
|
| ├────┼─┼─┼─┼─┼─┼─┤
|
1L 6s (onyx)
|
5, 2
|
5:2
|
| ├──┼─┼─┼─┼─┼─┼─┼─┤
|
1L 7s (antipine)
|
3, 2
|
3:2
|
| ├┼─┼─┼─┼─┼─┼─┼─┼─┤
|
8L 1s (subneutralic)
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Generators 16\17 and 1\17
| Step visualization
|
MOS (name)
|
Step sizes
|
Step ratio
|
| ├───────────────┼┤
|
1L 1s
|
16, 1
|
16:1
|
| ├──────────────┼┼┤
|
1L 2s
|
15, 1
|
15:1
|
| ├─────────────┼┼┼┤
|
1L 3s
|
14, 1
|
14:1
|
| ├────────────┼┼┼┼┤
|
1L 4s
|
13, 1
|
13:1
|
| ├───────────┼┼┼┼┼┤
|
1L 5s (antimachinoid)
|
12, 1
|
12:1
|
| ├──────────┼┼┼┼┼┼┤
|
1L 6s (onyx)
|
11, 1
|
11:1
|
| ├─────────┼┼┼┼┼┼┼┤
|
1L 7s (antipine)
|
10, 1
|
10:1
|
| ├────────┼┼┼┼┼┼┼┼┤
|
1L 8s (antisubneutralic)
|
9, 1
|
9:1
|
| ├───────┼┼┼┼┼┼┼┼┼┤
|
1L 9s (antisinatonic)
|
8, 1
|
8:1
|
| ├──────┼┼┼┼┼┼┼┼┼┼┤
|
1L 10s
|
7, 1
|
7:1
|
| ├─────┼┼┼┼┼┼┼┼┼┼┼┤
|
1L 11s
|
6, 1
|
6:1
|
| ├────┼┼┼┼┼┼┼┼┼┼┼┼┤
|
1L 12s
|
5, 1
|
5:1
|
| ├───┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
1L 13s
|
4, 1
|
4:1
|
| ├──┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
1L 14s
|
3, 1
|
3:1
|
| ├─┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
1L 15s
|
2, 1
|
2:1
|
| ├┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┤
|
17edo
|
1, 1
|
1:1
|
Gallery
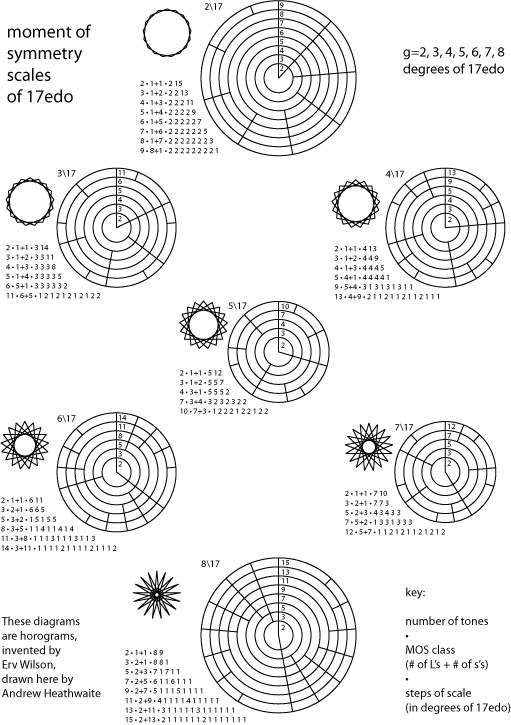
17edo horograms.pdf
See also
