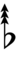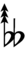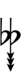96edo

← 95edo

96edo

97edo →

Prime factorization

2⁵ × 3

Step size

12.5¢

Fifth

56\96 (700¢) (→7\12)

Semitones (A1:m2)

8:8 (100¢ : 100¢)

Consistency limit

5

Distinct consistency limit

5

English Wikipedia has an article on:

96 equal temperament

96 equal divisions of the octave (abbreviated 96edo or 96ed2), also called 96-tone equal temperament (96tet) or 96 equal temperament (96et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 96 equal parts of exactly 12.5 ¢ each. Each step represents a frequency ratio of 2^1/96, or the 96th root of 2.

Theory

As a 5-limit system, 96edo can be characterized by the fact that it tempers out both the Pythagorean comma, 531441/524288, Würschmidt's comma, 393216/390625, the unicorn comma, 1594323/1562500, and the kwazy comma, [-53 10 16⟩. It therefore has the same familiar 700-cent fifth as 12edo, and has a best major third of 387.5 cents, a bit over a cent sharp. There is therefore nothing to complain of with its representation of the 5-limit and it can be recommended as an approach to the würschmidt family of temperaments. It also tempers out the unicorn comma, and serves a way of tuning temperaments in the unicorn family. It supports sitcom temperament.

One notable benefit of 96edo's representation of the 5-limit is that its dramatic narrowing of 81/80 allows for a less dissonant ~40/27 wolf fifth. This allows for the potential of a 12-note subset of 96edo being seen as a well temperament, and as part of an equal temperament, this scale could be rotated around during the run-time of a piece of music.

In the 7-limit, 96 has two possible mappings for 7/4, a sharp one of 975 cents from the patent val, and a flat one of 962.5 cents from 96d. Using the sharp mapping, 96 tempers out 225/224 and supports 7-limit würschmidt temperament, and using the flat mapping it tempers out 126/125 and supports worschmidt temperament. We can also dispense with 7 altogether, and use it as a no-sevens system, where it tempers out 243/242 in the 11-limit and 676/675 in the 13-limit. If we include 7, then the sharp mapping tempers out 99/98 and 176/175 in the 11-limit, and 169/168 in the 13-limit, and this provides the optimal patent val for the interpental temperament. With the flat 7 it tempers out 385/384 in the 11-limit and 196/195 and 364/363 in the 13-limit, and serves for the various temperaments of the unicorn family.

Prime harmonics

Approximation of prime harmonics in 96edo
Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	Absolute (¢)	+0.00	-1.96	+1.19	+6.17	-1.32	-3.03	-4.96	+2.49	-3.27	-4.58	+4.96
Error	Relative (%)	+0.0	-15.6	+9.5	+49.4	-10.5	-24.2	-39.6	+19.9	-26.2	-36.6	+39.7
Steps (reduced)		96 (0)	152 (56)	223 (31)	270 (78)	332 (44)	355 (67)	392 (8)	408 (24)	434 (50)	466 (82)	476 (92)

As a tuning standard

A step of 96edo is known as a triamu (third MIDI-resolution unit, 3mu, 2³ = 8 equal divisions of the 12edo semitone). The internal data structure of the 3mu requires one byte, with the first two bits reserved as flags, one to indicate the byte's status as data, and one to indicate the sign (+ or −) showing the direction of the pitch-bend up or down, and three other bits which are not used.

Subsets and supersets

Since 96 factors into 2⁵ × 3, 96edo has subset edos 2, 3, 4, 6, 8, 12, 16, 24, 32, and 48.

Intervals

Steps	Cents	Approximate ratios	Ups and downs notation
0	0	1/1	D
1	12.5		^D, ^E♭♭
2	25		^^D, ^^E♭♭
3	37.5	44/43	^³D, ^³E♭♭
4	50	34/33, 37/36	^⁴D, v⁴E♭
5	62.5		v³D♯, v³E♭
6	75	23/22, 24/23	vvD♯, vvE♭
7	87.5	20/19, 41/39	vD♯, vE♭
8	100	18/17	D♯, E♭
9	112.5	16/15	^D♯, ^E♭
10	125	29/27, 43/40	^^D♯, ^^E♭
11	137.5	13/12, 40/37	^³D♯, ^³E♭
12	150	12/11	^⁴D♯, v⁴E
13	162.5	11/10	v³D𝄪, v³E
14	175	21/19, 31/28	vvD𝄪, vvE
15	187.5	29/26	vD𝄪, vE
16	200	37/33	E
17	212.5	26/23, 35/31, 43/38	^E, ^F♭
18	225	33/29, 41/36	^^E, ^^F♭
19	237.5	39/34	^³E, ^³F♭
20	250	15/13, 37/32	^⁴E, v⁴F
21	262.5	43/37	v³E♯, v³F
22	275	27/23, 34/29	vvE♯, vvF
23	287.5	13/11	vE♯, vF
24	300	19/16, 25/21, 44/37	F
25	312.5		^F, ^G♭♭
26	325	41/34	^^F, ^^G♭♭
27	337.5		^³F, ^³G♭♭
28	350	11/9, 38/31	^⁴F, v⁴G♭
29	362.5	37/30	v³F♯, v³G♭
30	375	31/25, 36/29, 41/33	vvF♯, vvG♭
31	387.5	5/4	vF♯, vG♭
32	400	29/23, 34/27	F♯, G♭
33	412.5	33/26	^F♯, ^G♭
34	425	23/18, 32/25	^^F♯, ^^G♭
35	437.5		^³F♯, ^³G♭
36	450		^⁴F♯, v⁴G
37	462.5	17/13, 30/23	v³F𝄪, v³G
38	475	25/19	vvF𝄪, vvG
39	487.5		vF𝄪, vG
40	500	4/3	G
41	512.5	39/29, 43/32	^G, ^A♭♭
42	525	23/17, 42/31	^^G, ^^A♭♭
43	537.5	15/11	^³G, ^³A♭♭
44	550	11/8	^⁴G, v⁴A♭
45	562.5	18/13	v³G♯, v³A♭
46	575		vvG♯, vvA♭
47	587.5		vG♯, vA♭
48	600	41/29	G♯, A♭
49	612.5	37/26	^G♯, ^A♭
50	625	33/23, 43/30	^^G♯, ^^A♭
51	637.5	13/9	^³G♯, ^³A♭
52	650	16/11	^⁴G♯, v⁴A
53	662.5	22/15	v³G𝄪, v³A
54	675	31/21, 34/23	vvG𝄪, vvA
55	687.5		vG𝄪, vA
56	700	3/2	A
57	712.5		^A, ^B♭♭
58	725	38/25, 41/27	^^A, ^^B♭♭
59	737.5	23/15, 26/17	^³A, ^³B♭♭
60	750	37/24	^⁴A, v⁴B♭
61	762.5		v³A♯, v³B♭
62	775	25/16, 36/23	vvA♯, vvB♭
63	787.5	41/26	vA♯, vB♭
64	800	27/17	A♯, B♭
65	812.5	8/5	^A♯, ^B♭
66	825	29/18, 37/23	^^A♯, ^^B♭
67	837.5		^³A♯, ^³B♭
68	850	18/11, 31/19	^⁴A♯, v⁴B
69	862.5		v³A𝄪, v³B
70	875		vvA𝄪, vvB
71	887.5		vA𝄪, vB
72	900	32/19, 37/22, 42/25	B
73	912.5	22/13, 39/23	^B, ^C♭
74	925	29/17, 41/24	^^B, ^^C♭
75	937.5	43/25	^³B, ^³C♭
76	950	26/15	^⁴B, v⁴C
77	962.5		v³B♯, v³C
78	975		vvB♯, vvC
79	987.5	23/13	vB♯, vC
80	1000	41/23	C
81	1012.5		^C, ^D♭♭
82	1025	38/21	^^C, ^^D♭♭
83	1037.5	20/11	^³C, ^³D♭♭
84	1050	11/6	^⁴C, v⁴D♭
85	1062.5	24/13, 37/20	v³C♯, v³D♭
86	1075		vvC♯, vvD♭
87	1087.5	15/8	vC♯, vD♭
88	1100	17/9	C♯, D♭
89	1112.5	19/10	^C♯, ^D♭
90	1125	23/12, 44/23	^^C♯, ^^D♭
91	1137.5		^³C♯, ^³D♭
92	1150	33/17	^⁴C♯, v⁴D
93	1162.5	43/22	v³C𝄪, v³D
94	1175		vvC𝄪, vvD
95	1187.5		vC𝄪, vD
96	1200	2/1	D

Notation

Ups and downs notation

96edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:

Semitones	0	1⁄8	1⁄4	3⁄8	1⁄2	5⁄8	3⁄4	7⁄8	1	1+1⁄8	1+1⁄4	1+3⁄8	1+1⁄2	1+5⁄8	1+3⁄4	1+7⁄8	2	2+1⁄8	2+1⁄4	2+3⁄8
Sharp Symbol
Flat Symbol

Approximation to JI

The following tables show how 15-odd-limit intervals are represented in 96edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 96edo (direct approximation, even if inconsistent)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
15/11, 22/15	0.549	4.4
11/6, 12/11	0.637	5.1
15/8, 16/15	0.769	6.1
13/9, 18/13	0.882	7.1
13/12, 24/13	1.073	8.6
5/4, 8/5	1.186	9.5
11/8, 16/11	1.318	10.5
13/11, 22/13	1.710	13.7
3/2, 4/3	1.955	15.6
15/13, 26/15	2.259	18.1
9/7, 14/9	2.416	19.3
11/10, 20/11	2.504	20.0
11/9, 18/11	2.592	20.7
13/8, 16/13	3.028	24.2
5/3, 6/5	3.141	25.1
13/7, 14/13	3.298	26.4
9/8, 16/9	3.910	31.3
13/10, 20/13	4.214	33.7
7/6, 12/7	4.371	35.0
7/5, 10/7	4.988	39.9
11/7, 14/11	5.008	40.1
9/5, 10/9	5.096	40.8
15/14, 28/15	5.557	44.5
7/4, 8/7	6.174	49.4

15-odd-limit intervals in 96edo (patent val mapping)
Interval and complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
15/11, 22/15	0.549	4.4
11/6, 12/11	0.637	5.1
15/8, 16/15	0.769	6.1
13/9, 18/13	0.882	7.1
13/12, 24/13	1.073	8.6
5/4, 8/5	1.186	9.5
11/8, 16/11	1.318	10.5
13/11, 22/13	1.710	13.7
3/2, 4/3	1.955	15.6
15/13, 26/15	2.259	18.1
11/10, 20/11	2.504	20.0
11/9, 18/11	2.592	20.7
13/8, 16/13	3.028	24.2
5/3, 6/5	3.141	25.1
9/8, 16/9	3.910	31.3
13/10, 20/13	4.214	33.7
7/5, 10/7	4.988	39.9
9/5, 10/9	5.096	40.8
7/4, 8/7	6.174	49.4
15/14, 28/15	6.943	55.5
11/7, 14/11	7.492	59.9
7/6, 12/7	8.129	65.0
13/7, 14/13	9.202	73.6
9/7, 14/9	10.084	80.7

Zeta peak index

Tuning			Strength			Closest edo		Integer limit
ZPI	Steps per octave	Step size (cents)	Height	Integral	Gap	Edo	Octave (cents)	Consistent	Distinct
546zpi	95.9543940692998	12.5059410946136	7.327322	1.045052	15.480737	96edo	1200.57034508290	6	6

Regular temperament properties

Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Absolute (¢)	Relative (%)
2.3.5	393216/390625, 531441/524288	[⟨96 152 223]]	+0.240	0.732	5.86
2.3.5.11	243/242, 5632/5625, 131769/131072	[⟨96 152 223 332]]	+0.276	0.637	5.10

Rank-2 temperaments

Periods per 8ve	Generator*	Cents*	Associated ratio*	Temperament
1	5\96	62.5	28/27	Unicorn / camahueto (96d)
1	21\96	262.5	64/55	Spog
1	29\96	362.5	16/13	Submajor / interpental (96)
1	31\96	387.5	5/4	Würschmidt (96) / worschmidt (96d)
2	5\96	62.5	28/27	Monocerus (96d)
2	13\96	162.5	11/10	Gwazy (96) / bisupermajor (96d)
2	25\96	312.5	6/5	Vines (96d)
12	31\96 (1\96)	387.5 (12.5)	5/4 (126/125)	Compton (7-limit, 96)
24	31\96 (1\96)	387.5 (12.5)	5/4 (245/243)	Hours (96d)

Scales

5- to 10-tone scales in 96edo

History

96 equal divisions of the octave was first used by the Mexican composer and theorist Julián Carrillo. It has subsequently been used by a number of other composers.