196608edo
| ← 196607edo | 196608edo | 196609edo → |
196608 equal divisions of the octave (abbreviated 196608edo or 196608ed2), also called 196608-tone equal temperament (196608tet) or 196608 equal temperament (196608et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 196608 equal parts of about 0.0061 ¢ each. Each step represents a frequency ratio of 21/196608, or the 196608th root of 2.
Theory
196608edo is enfactored in the 17-limit, having the same tuning as 98304edo, which is quite an efficient system in itself. In that regard, 196608edo provides barely anything new apart from most characteristics of what it doubles.
As a tuning standard
A step of 196608edo is known as a MIDI Tuning Standard unit (MTSU) or a tetradecamu (fourteenth MIDI-resolution unit, 14mu, 214 = 16384 equal divisions of the 12edo semitone). The 14mu is specified in the MIDI spec (1983) as the smallest increment available for the pitch-bend controller, and as the frequency data format for MTS (1999). The 14mu is the smallest unit of tuning resolution which has ever been put into common musical use, and provides extremely accurate tuning in microtonal electronic music.
The main application of 196608edo is thus not as a compositional device, but as a technical tuning standard. If we adopt direct approximation, some JI intervals are indeed improved, which makes sense since we are only quantizing JI to the grid of this edo.
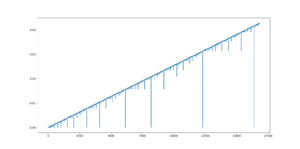
Another usage that is not commonly seen in other edos is to approximate smaller edos. It cannot approximate any larger edos or any edos of the same order of magnitude. From the diagram we can observe the maximum relative errors of smallers edos are mostly linear with respect to the edo number. 16808edo, a notable zeta edo that is an order of magnitude below, is approximated with a ~4% maximum relative error.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.00188 | +0.00220 | -0.00266 | +0.00235 | +0.00042 | -0.00032 | +0.00033 | +0.00065 | +0.00285 | +0.00156 | -0.00286 |
| Relative (%) | -30.7 | +36.1 | -43.7 | +38.5 | +6.8 | -5.2 | +5.4 | +10.6 | +46.7 | +25.6 | -46.9 | |
| Steps (reduced) |
311616 (115008) |
456510 (63294) |
551948 (158732) |
623233 (33409) |
680152 (90328) |
727536 (137712) |
768126 (178302) |
803628 (17196) |
835177 (48745) |
863565 (77133) |
889368 (102936) | |
Selected intervals
Below is a list for just intervals.
| # | Cents | JI Interval | Error (Steps) |
Error (Cents) | |
|---|---|---|---|---|---|
| Ratio | Cents | ||||
| 0 | 0.000000000000 | 1/1 | 0.000000000000 | ±0.000000 | ±0.000000000000 |
| 18306 | 111.730957031250 | 16/15 | 111.731285269778 | −0.053779 | −0.000328238528 |
| 19570 | 119.445800781250 | 15/14 | 119.442808261097 | +0.490295 | +0.002992520153 |
| 21020 | 128.295898437500 | 14/13 | 128.298244699814 | −0.384412 | −0.002346262314 |
| 22704 | 138.574218750000 | 13/12 | 138.572660903923 | +0.255238 | +0.001557846077 |
| 24680 | 150.634765625000 | 12/11 | 150.637058500631 | −0.375665 | −0.002292875631 |
| 27034 | 165.002441406250 | 11/10 | 165.004228499922 | −0.292797 | −0.001787093672 |
| 29885 | 182.403564453125 | 10/9 | 182.403712134060 | −0.024196 | −0.000147680935 |
| 33409 | 203.912353515625 | 9/8 | 203.910001730775 | +0.385316 | +0.002351784850 |
| 37876 | 231.176757812500 | 8/7 | 231.174093530875 | +0.436516 | +0.002664281625 |
| 40590 | 247.741699218750 | 15/13 | 247.741052960912 | +0.105883 | +0.000646257838 |
| 43724 | 266.870117187500 | 7/6 | 266.870905603738 | −0.129174 | −0.000788416238 |
| 47384 | 289.208984375000 | 13/11 | 289.209719404554 | −0.120427 | −0.000735029554 |
| 51715 | 315.643310546875 | 6/5 | 315.641287000553 | +0.331538 | +0.002023546322 |
| 56919 | 347.406005859375 | 11/9 | 347.407940633982 | −0.316993 | −0.001934774607 |
| 58896 | 359.472656250000 | 16/13 | 359.472338230689 | +0.052104 | +0.000318019311 |
| 63294 | 386.315917968750 | 5/4 | 386.313713864835 | +0.361120 | +0.002204103915 |
| 68405 | 417.510986328125 | 14/11 | 417.507964104368 | +0.495161 | +0.003022223757 |
| 71284 | 435.083007812500 | 9/7 | 435.084095261650 | −0.178168 | −0.001087449150 |
| 74418 | 454.211425781250 | 13/10 | 454.213947904476 | −0.413225 | −0.002522123226 |
| 81600 | 498.046875000000 | 4/3 | 498.044999134613 | +0.307342 | +0.001875865387 |
| 87974 | 536.950683593750 | 15/11 | 536.950772365466 | −0.014544 | −0.000088771716 |
| 90328 | 551.318359375000 | 11/8 | 551.317942364757 | +0.068323 | +0.000417010243 |
| 92305 | 563.385009765625 | 18/13 | 563.382339961464 | +0.437421 | +0.002669804161 |
| 95439 | 582.513427734375 | 7/5 | 582.512192604290 | +0.202364 | +0.001235130085 |
| 101169 | 617.486572265625 | 10/7 | 617.487807395710 | −0.202364 | −0.001235130085 |
| 106280 | 648.681640625000 | 16/11 | 648.682057635243 | −0.068323 | −0.000417010243 |
| 115008 | 701.953125000000 | 3/2 | 701.955000865387 | −0.307342 | −0.001875865387 |
| 125324 | 764.916992187500 | 14/9 | 764.915904738350 | +0.178168 | +0.001087449150 |
| 128203 | 782.489013671875 | 11/7 | 782.492035895632 | −0.495161 | −0.003022223757 |
| 133314 | 813.684082031250 | 8/5 | 813.686286135165 | −0.361120 | −0.002204103915 |
| 139689 | 852.593994140625 | 18/11 | 852.592059366018 | +0.316993 | +0.001934774607 |
| 144893 | 884.356689453125 | 5/3 | 884.358712999447 | −0.331538 | −0.002023546322 |
| 152884 | 933.129882812500 | 12/7 | 933.129094396262 | +0.129174 | +0.000788416238 |
| 158732 | 968.823242187500 | 7/4 | 968.825906469125 | −0.436516 | −0.002664281625 |
| 163199 | 996.087646484375 | 16/9 | 996.089998269225 | −0.385316 | −0.002351784850 |
| 166723 | 1017.596435546875 | 9/5 | 1017.596287865940 | +0.024196 | +0.000147680935 |
| 169574 | 1034.997558593750 | 20/11 | 1034.995771500078 | +0.292797 | +0.001787093672 |
| 171928 | 1049.365234375000 | 11/6 | 1049.362941499369 | +0.375665 | +0.002292875631 |
| 196608 | 1200.000000000000 | 2/1 | 1200.000000000000 | ±0.000000 | ±0.000000000000 |
See also
- Interval size measure
- Equal multiplications of MIDI-resolution units