15edo
| ← 14edo | 15edo | 16edo → |
15 equal divisions of the octave (abbreviated 15edo or 15ed2), also called 15-tone equal temperament (15tet) or 15 equal temperament (15et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 15 equal parts of exactly 80 ¢ each. Each step represents a frequency ratio of 21/15, or the 15th root of 2.
Theory
15edo can be thought of as three sets of 5edo which do not connect by fifths. The fifth at 720 cents is quite wide yet still usable as a perfect fifth. Some would describe the fifth as more shimmery and pungent than anything closer to a just 3/2. 15edo contains 3 circles of five 3/2s (supporting blackwood, which tempers out the Pythagorean limma), and 5 circles of three 5/4s (supporting augmented temperament). This is radically different than a meantone system, and has a variety of ramifications for chord progressions based on diatonic functional harmony, because if you use the equipentatonic as your "diatonic scale", the same interval can have multiple functions.
A useful way to visualize the pitches and intervals of 15edo is to arrange the notes in a grid, with 3/2s or 7/4s on one axis and 5/4s on the other, to create a 3x5 rectangle of notes which tiles the plane.
15edo shares 5edo's 2.3.7 subgroup tuning (and thus supports superpyth, slendric, and semaphore, like 5edo). However, by splitting each 5edo step into three parts, reasonable approximations to 5/4 and 11/8 are obtained (as per valentine temperament), so 15edo can reasonably be described as an 11-limit temperament, and is generally considered to be the first edo to work as an 11-limit system; however, due to its rather distant approximation of the 3rd harmonic (and therefore the 9th harmonic as well), those seeking to represent JI with 15edo would be best advised to avoid chords requiring those harmonics (or to at least treat them with sensitivity, for instance, only using 9/8 when it is being made up of two 3/2s to make its identity clear). 15edo is also notable for being the smallest edo with recognizable, distinct representations of 5-odd limit intervals (3/2, 5/4, 6/5, and their octave inverses) that has a positive syntonic comma.
In the 15edo system, major thirds cannot be divided perfectly into two, while minor thirds, fourths, wide tritones, subminor sevenths, and supermajor sevenths can. Similarly, supermajor seconds, fourths, fifths, and subminor sevenths can all be divided into 3 equal parts, while minor thirds, tritones, and major sixths cannot.
This gives 15edo a whole new set of pitch symmetries and modes of limited transposition. Coupled with the lack of a 5L 2s diatonic scale and of a standard tritone, this tuning can be disorienting at first. Nonetheless, 15edo is notable for being the next-smallest edo after 9edo, 12edo and 14edo that contains recognizable major and minor triads. Under a stricter definition excluding 9edo and 14edo, this is a property noted in the works of theorists like Ivor Darreg and Easley Blackwood. In addition, because the guitar can be tuned symmetrically, from E to e (6th to 1st strings) unlike the 12-tone system on guitars, the learning curve is very manageable. All chords look the same modulated anywhere, and minor arpeggios are vertically stacked, making them very easy to play. 15-tone may be a promising start for anyone interested in xenharmony, due to its manageable number of tones and for containing the relatively popular 5edo.
A possible analogue to the diatonic scale in 15edo is the Zarlino diatonic, which flattens one fifth to a large tritone in order to make all 7 notes distinct (and close to corresponding JI intervals, especially if you use the left-handed version). The fact that 15edo supports porcupine temperament is equivalent to the fact that both accidentals generally required to notate zarlino collapse to a single chromatic step. For a moment-of-symmetry scale, the 1L 6s (onyx) and 5L 5s (blackwood) scales are also an option.
15edo is also the second-smallest edo (after 10edo) that maintains 25% or lower relative error on all of the first eight harmonics of the harmonic series.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +18.0 | +13.7 | -8.8 | +8.7 | +39.5 | -25.0 | +22.5 | +11.7 | +10.4 | -25.0 |
| Relative (%) | +0.0 | +22.6 | +17.1 | -11.0 | +10.9 | +49.3 | -31.2 | +28.1 | +14.7 | +13.0 | -31.3 | |
| Steps (reduced) |
15 (0) |
24 (9) |
35 (5) |
42 (12) |
52 (7) |
56 (11) |
61 (1) |
64 (4) |
68 (8) |
73 (13) |
74 (14) | |
Composition theory
- Unque's approach - covers scales, chords, intervals, and functional harmony.
- Vector's guides - covers the construction of scales, the kinds of chords found in 15edo, and a possible notation system.
- Astaryuu's notes - covers notation, scales, modes, intervals, and chords so far.
- Metallic harmony - harmony involving stacking sevenths instead of thirds; 15edo is one of the systems it is intended for.
Intervals
Relative to 12edo, 15edo maintains some categorically-similar intervals, particularly the 3rds, 4ths, 5ths, and 6ths, but is quite different in the categories of 2nds and 7ths. The closest intervals it has to a 12edo whole tone are both 40 cents sharp or flat of the 200-cent 12edo whole tone. This makes it rather difficult to translate traditional diatonic melodic approaches into 15edo, and also means that things like 7th, 9th, and 11th chords will behave very differently, even though major and minor triads are still relatively familiar-sounding. One step of 15edo almost exactly equals the reduced 67th harmonic, 67/64.
| Degree | Cents | Approximate Ratios[note 1] | Solfege (porcupine-based) |
Porcupine[7] (traditional) |
Porcupine[8] (Greek) |
Zarlino diatonic notation | Blackwood "guitar notation" |
Blackwood Decimal |
Audio |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1/1 | do | D | α | C | E | 1 | |
| 1 | 80 | 25/24, 21/20, 16/15, 22/21 | di | D# / Eb | α/ β\ | Db / C# | E# | 1# / 2b | |
| 2 | 160 | 11/10, 12/11, 10/9 | ru | E | β | D | Gb | 2 | |
| 3 | 240 | 8/7, 7/6, 9/8 | re | E# / Fb | β/ χ\ | D# | G | 3 | |
| 4 | 320 | 6/5, 11/9 | me | F | χ | Eb | G# | 3# / 4b | |
| 5 | 400 | 5/4, 14/11 | mi | F# / Gb | χ/ δ\ | E | Ab | 4 | |
| 6 | 480 | 4/3, 9/7, 21/16 | fa | G | δ | F | A | 5 | |
| 7 | 560 | 11/8, 7/5 | fu | G# | δ/ ε\ | F# | A# | 5# / 6b | |
| 8 | 640 | 16/11, 10/7 | su | Ab | ε | Gb | Bb | 6 | |
| 9 | 720 | 3/2, 14/9, 32/21 | sol | A | ε/ φ\ | G | B | 7 | |
| 10 | 800 | 8/5, 11/7 | le | A# / Bb | φ | Ab / G# | B# | 7# / 8b | |
| 11 | 880 | 5/3, 18/11 | la | B | φ/ γ\ | A | Db | 8 | |
| 12 | 960 | 7/4, 12/7, 16/9 | ta | B# / Cb | γ | A# / Bbb | D | 9 | |
| 13 | 1040 | 20/11, 11/6, 9/5 | tu | C | γ/ η\ | Bb | D# | 9# / 0b | |
| 14 | 1120 | 48/25, 40/21, 15/8, 21/11 | ti | C# / Db | η | B | Eb | 0 | |
| 15 | 1200 | 2/1 | do | D | α | C | E | 1 |
Alternative interval names
| Step | Cents | Ups and downs notation (EUs: v3A1 and m2) (partial list, e.g. M2/m3 is also A1 and d4) |
Porcupine notation (EU: dd2) | |||
|---|---|---|---|---|---|---|
| 0 | 0 | P1, m2 | unison, min 2nd | C# / D / Eb | unison | D |
| 1 | 80 | ^1, ^m2 | up-unison, upminor 2nd | ^C# / ^D / ^Eb | aug unison, dim 2nd | D# / Eb |
| 2 | 160 | vM2 | downmajor 2nd | vD# / vE / vF / vGb | perfect 2nd | E |
| 3 | 240 | M2, m3 | major 2nd, minor 3rd | D# / E / F / Gb | aug 2nd, dim 3rd | E# / Fb |
| 4 | 320 | ^m3 | upminor 3rd | ^D# / ^E / ^F / ^Gb | minor 3rd | F |
| 5 | 400 | vM3 | downmajor 3rd | vF# / vG / vAb | major 3rd, dim 4th | F# / Gb |
| 6 | 480 | M3, P4, d5 | major 3rd, perfect 4th, dim 5th | F# / G / Ab | aug 3rd, minor 4th | Fx / G |
| 7 | 560 | ^4, ^d5 | up 4th, updim 5th | ^F# / ^G / ^Ab | major 4th, dim 5th | G# / Abb |
| 8 | 640 | vA4, v5 | downaug 4th, down 5th | vG# / vA / vBb | aug 4th, minor 5th | Gx / Ab |
| 9 | 720 | A4, P5, m6 | aug 4th, perfect 5th, minor 6th | G# / A / Bb | major 5th, dim 6th | A / Bbb |
| 10 | 800 | ^5, ^m6 | up 5th, upminor 6th | ^G# / ^A / ^Bb | aug 5th, minor 6th | A# / Bb |
| 11 | 880 | vA5, vM6 | downaug 5th, downmajor 6th | vA# / vB / vC / vDb | major 6th | B |
| 12 | 960 | M6, m7 | major 6th, minor 7th | A# / B / C / Db | aug 6th, dim 7th | B# / Cb |
| 13 | 1040 | ^m7 | upminor 7th | ^A# / ^B / ^C / ^Db | perfect 7th | C |
| 14 | 1120 | vM7, v8 | downmajor 7th, down octave | vC# / vD / vEb | aug 7th, dim 8ve | C# / Db |
| 15 | 1200 | M7, P8 | major 7th, octave | C# / D / Eb | 8ve | D |
The 15edo porcupine genchain in both absolute and relative notation:
- …Fx — Gx — A# — B# — C# — D# — E# — F# — G# — A — B — C — D — E — F — G — Ab — Bb — Cb — Db — Eb — Fb — Gb — Abb — Bbb…
- …A3 — A4 — A5 — A6 — A7 — A1 — A2 — M3 — M4 — M5 — M6 — P7 — P1 — P2 — m3 — m4 — m5 — m6 — d7 — d8 — d2 — d3 — d4 — d5 — d6…
All 15edo chords can be named using ups and downs. Because many intervals have several names, many chords do too. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).
0-3-9 = D E A = D2 = "D sus 2", or D F A = Dm = "D minor" (approximate 6:7:9)
0-4-9 = D ^F A = D^m = "D upminor" (approximate 10:12:15)
0-5-9 = D vF# A = Dv = "D down" or "D downmajor" (approximate 4:5:6)
0-6-9 = D G A = D4, or D F# A = D = "D" or "D major" (approximate 14:18:21)
0-3-9-12 = D F A C = Dm7 = "D minor seven", or D F A B = Dm6 = "D minor six"
0-4-9-12 = D ^F A C = D^m,7 = "D upminor, add seven", or D ^F A B = D^m,6 = "D upminor add-six"
0-5-9-12 = D vF# A C = Dv,7 = "D down add-seven", or D vF# A B = Dv,6 = "D down add-six"
0-6-9-12 = D F# A C = D7 = "D seven", or D F# A B = D6 = "D six"
0-5-9-14 = D vF# A vC# = DvM7 = "D downmajor seven"
0-4-9-13 = D ^F A ^C = D^m7 = "D upminor-seven", or D ^F A ^B = D^m6 = "D upminor-six"
For a more complete list, see Ups and downs notation#Chords and Chord Progressions.
Notation
There are many ways to notate 15edo, and the choice of notation depends heavily on which temperament or scale one wishes to focus on.
Notations generated by the fifth
In these notations, the nominals form a circle of perfect fifths. The other notes are notated using accidentals that raise or lower by one edostep.
Ups and downs notation (heptatonic)
15edo can be notated with ups and downs, spoken as up, dup, downsharp, sharp, upsharp etc. and down, dud, upflat etc. Note that downsharp is equivalent to dup (double-up) and upflat is equivalent to dud (double-down).
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
||||||
| Flat symbol | |
|
Alternative symbols for ups and downs notation uses sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
"Eef" notation (pentatonic)
Kite Giedraitis proposes pentatonic (as opposed to heptatonic) note names that omit B and merge E and F into a new letter "eef" that rhymes with "leaf". Eef, like E, is a 5th above A. Eef, like F, is a 4th above C. Eef is written like an E, but with the bottom horizontal line going not right but left from the vertical line. Eef can be typed as ꘙ (unicode A619) or ⊧ (unicode 22A7) or 𐐆 (unicode 10406). The circle of 5ths is C G D A ꘙ C. All intervals are either perfect, upperfect or dowperfect (never major or minor). This is similar to heptatonic interval names in 7edo, 14edo, 21edo, etc.
| C | ^C | vD | D | ^D | vꘙ | ꘙ | ^ꘙ | vG | G | ^G | vA | A | ^A | vC | C |
| P1 | ^1 | v2 | P2 | ^2 | v3 | P3 | ^3 | v4 | P4 | ^4 | v5 | P5 | ^5 | v6 | P6 |
Sagittal notation (heptatonic)
This notation uses the same sagittal sequence as EDOs 22 and 29, is a subset of the notation for 30-EDO, and is a superset of the notation for 5-EDO.

Blackwood guitar notation
On a 15edo guitar, because the "perfect fourth" comes from 5edo, all of the open strings can be tuned a perfect fourth apart and still span exactly two octaves. If one starts the circle of fourths on B — B-E-A-D-G-(B) — then the open strings of the guitar can be notated as usual (E-A-D-G-B-E). However, because the circle of fourths closes at five, and does not continue to circulate through the other 10 notes of 15edo, it is necessary to use accidentals to notate intervals on the other two chains of 5edo. This notation is not particularly ideal as a basis for a staff notation (as it requires all non-5edo chords to be notated with accidentals). It is nevertheless useful because it reflects an intuitive approach to 15edo on the guitar, since 5edo provides a useful set of 3-limit landmarks (or "perfect fourths" and "perfect fifths") that can be used to navigate the fretboard. It's especially convenient for writing chord charts, where the funky accidental-laden spellings can be more or less ignored.
Blackwood decatonic notation
Using the nominals 1-0 (with 0 representing "10"), one of the three circles of 5edo is represented by the odd numbers, the second by the even numbers, and the third by numbers with accidentals (either odd numbers with sharps, or even numbers with flats).
One could name the nominals with letters instead of numbers, such as ABC... or JKL...
Notations generated by the second
In these notations, the nominals form a chain of perfect 2nds, each of which are two edosteps wide. From the last note of the chain up to the first there is an augmented 2nd of three edosteps. Accidentals raise or lower by one edostep.
Porcupine notation (heptatonic)
Porcupine notation can be based on the Porcupine[7] Lssssss scale. By representing the 3|3 mode (sssLsss) with a chain of seconds (D E F G A B C D) and using sharps and flats (#/b) to denote an edostep up or down respectively, 15edo can be notated using standard notation. Its intervals are here named with respect to diatonic intervals, i.e., as if fifth-generated. Thus the 4th and 5th are called perfect even though they are not generators, and the 2nd and 7th are not called perfect even though they are generators.
| Cents | Interval Name(s) | Note name(s) | Diamond-mos (on symmetric mode) |
|---|---|---|---|
| 0 | Unison | D | J |
| 80 | Augmented Unison / Minor Second | D# / Eb | J&/K@ |
| 160 | Major Second | E | K |
| 240 | Augmented Second / Diminished Third | E# / Fb | K&/L@ |
| 320 | Minor Third | F | L |
| 400 | Major Third / Diminished Fourth | F# / Gb | L&/M@ |
| 480 | Perfect Fourth | G | M |
| 560 | Augmented Fourth | G# | M& |
| 640 | Diminished Fifth | Ab | N@ |
| 720 | Perfect Fifth | A | N |
| 800 | Augmented Fifth / Minor Sixth | A# / Bb | N&/O@ |
| 880 | Major Sixth | B | O |
| 960 | Augmented Sixth / Diminished Seventh | B# / Cb | O&/P@ |
| 1040 | Minor Seventh | C | P |
| 1120 | Major Seventh / Diminished Octave | C# / Db | P&/J@ |
| 1200 | Octave | D | J |
One advantage of this notation is that its notated D major scale, D E F# G A B C# D, directly corresponds to 15edo’s zarlino LH Ionian scale. However, this only holds true for the key of D. Furthermore, the perfect 4th and/or 5th of most other keys is notated the same way a diminished or augmented fourth or fifth is in standard diatonic. For example, in the key of A the perfect fifth is E#.
Zarlino notation (heptatonic)
15edo's zarlino scale can also be treated as the primary scale, analogously to diatonic.
| Cents | Note name(s) |
|---|---|
| 0 | D |
| 80 | D# |
| 160 | Eb |
| 240 | E |
| 320 | F |
| 400 | F# |
| 480 | Gb |
| 560 | G |
| 640 | G# / Ab |
| 720 | A |
| 800 | A# |
| 880 | Bb |
| 960 | B |
| 1040 | C |
| 1120 | C# / Db |
| 1200 | D |
Porcupine "quill" notation (octatonic)
Porcupine notation can also be based on the Porcupine[8] LLLLLLLs scale using eight nominals: either α β χ δ ε φ γ η or A B C D E F G H. Latin letters are easier to type and more generalizable, but they have the downside of conflicts with standard notation. Thus, Greek letters can be used in their place with a close resemblance to the spelling of ABCDEFGHA. The letters are not in greek alphabetic order.
The eight nominals form the base diatonic scale. In the "quill name" column, the "quill" is the name given to the two-edostep interval (160¢) of 15edo while the "small quill" (80¢) is the chroma of 15edo. This produces a very consistent notation for both Porcupine[8] and Blackwood[10], moreso than putting 15edo into a 5L 2s framework.
| Cents | Quill Name | MOSstep Name | Note names (Greek) | Note names (Latin) |
|---|---|---|---|---|
| 0 | Zeroquill | Perfect 0-step | α - α | A - A |
| 80 | Small Quill / Half Quill | Diminished 1-step | α - β\ | A - Bb |
| 160 | Quill | Perfect 1-step | α - β | A - B |
| 240 | Small Diquill | Minor 2-step | α - χ\ | A - Cb |
| 320 | Large Diquill | Major 2-step | α - χ | A - C |
| 400 | Small Triquill | Minor 3-step | α - δ\ | A - Db |
| 480 | Large Triquill | Major 3-step | α - δ | A - D |
| 560 | Small Fourquill | Minor 4-step | α - ε\ | A - Eb |
| 640 | Large Fourquill | Major 4-step | α - ε | A - E |
| 720 | Small Fivequill | Minor 5-step | α - φ\ | A - Fb |
| 800 | Large Fivequill | Major 5-step | α - φ | A - F |
| 880 | Small Sixquill | Minor 6-step | α - γ\ | A - Gb |
| 960 | Large Sixquill | Major 6-step | α - γ | A - G |
| 1040 | Small Sevenquill | Perfect 7-step | α - η\ | A - Hb |
| 1120 | Large Sevenquill | Augmented 7-step | α - η | A - H |
| 1200 | Octoquill | Perfect 8-step | α - α | A - A |
A regular keyboard can be designed using this system by placing 7 black keys as Porcupine[7] and 8 whites as Porcupine[8]. In fact, Stephen Weigel has already done this with his pink Halberstadt keyboard.
Approximation to JI

15edo offers some minor improvements over 12et in ratios of 5 (particularly in 6/5 and 5/3), and has a much better approximation to the 7th and 11th harmonics, but its approximation to the 3rd harmonic is rather off. However, the particular way in which this approximation is off is as much a feature as it is a bug, for it allows the construction of a 5L 5s MOS scale wherein every note of the scale can serve as a root for a 7-limit otonal or utonal tetrad, as well as either a 5-limit major or minor 7th chord. This is known as the blackwood temperament, named after Easley Blackwood Jr., who is the first to document its existence. It has also been written on extensively by Igliashon Jones in the paper Five is Not an Odd Number. For an in-depth treatment of harmony in 15edo based on this temperament (and its 7- and 11-limit extensions), see Blacksmith temperament modal harmony (in 15edo).
15-odd-limit interval mappings
The following tables show how 15-odd-limit intervals are represented in 15edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/9, 18/13 | 3.382 | 4.2 |
| 5/3, 6/5 | 4.359 | 5.4 |
| 11/10, 20/11 | 5.004 | 6.3 |
| 15/13, 26/15 | 7.741 | 9.7 |
| 11/8, 16/11 | 8.682 | 10.9 |
| 7/4, 8/7 | 8.826 | 11.0 |
| 11/6, 12/11 | 9.363 | 11.7 |
| 5/4, 8/5 | 13.686 | 17.1 |
| 11/7, 14/11 | 17.508 | 21.9 |
| 3/2, 4/3 | 18.045 | 22.6 |
| 13/12, 24/13 | 21.427 | 26.8 |
| 9/5, 10/9 | 22.404 | 28.0 |
| 7/5, 10/7 | 22.512 | 28.1 |
| 15/11, 22/15 | 23.049 | 28.8 |
| 13/10, 20/13 | 25.786 | 32.2 |
| 7/6, 12/7 | 26.871 | 33.6 |
| 11/9, 18/11 | 27.408 | 34.3 |
| 13/11, 22/13 | 30.790 | 38.5 |
| 13/7, 14/13 | 31.702 | 39.6 |
| 15/8, 16/15 | 31.731 | 39.7 |
| 9/7, 14/9 | 35.084 | 43.9 |
| 9/8, 16/9 | 36.090 | 45.1 |
| 15/14, 28/15 | 39.443 | 49.3 |
| 13/8, 16/13 | 39.472 | 49.3 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 13/9, 18/13 | 3.382 | 4.2 |
| 5/3, 6/5 | 4.359 | 5.4 |
| 11/10, 20/11 | 5.004 | 6.3 |
| 15/13, 26/15 | 7.741 | 9.7 |
| 11/8, 16/11 | 8.682 | 10.9 |
| 7/4, 8/7 | 8.826 | 11.0 |
| 11/6, 12/11 | 9.363 | 11.7 |
| 5/4, 8/5 | 13.686 | 17.1 |
| 11/7, 14/11 | 17.508 | 21.9 |
| 3/2, 4/3 | 18.045 | 22.6 |
| 13/12, 24/13 | 21.427 | 26.8 |
| 9/5, 10/9 | 22.404 | 28.0 |
| 7/5, 10/7 | 22.512 | 28.1 |
| 15/11, 22/15 | 23.049 | 28.8 |
| 13/10, 20/13 | 25.786 | 32.2 |
| 7/6, 12/7 | 26.871 | 33.6 |
| 11/9, 18/11 | 27.408 | 34.3 |
| 13/11, 22/13 | 30.790 | 38.5 |
| 15/8, 16/15 | 31.731 | 39.7 |
| 9/8, 16/9 | 36.090 | 45.1 |
| 13/8, 16/13 | 39.472 | 49.3 |
| 15/14, 28/15 | 40.557 | 50.7 |
| 9/7, 14/9 | 44.916 | 56.1 |
| 13/7, 14/13 | 48.298 | 60.4 |
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 47zpi | 15.05349 | 79.715734 | 5.050324 | 4.390681 | 1.104057 | 14.918297 | 1195.736016 | −4.263984 | 8 | 7 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
|
Absolute (¢) |
Relative (%) | ||||
| 2.3.5 | 128/125, 250/243 | [⟨15 24 35]] | −5.75 | 4.63 | 5.81 |
| 2.3.5.7 | 28/27, 49/48, 126/125 |
[⟨15 24 35 42]] |
−3.55 | 5.56 | 6.97 |
| 2.3.5.7.11 | 28/27, 49/48, 55/54, 77/75 | [⟨15 24 35 42 52]] | −3.34 | 4.99 | 6.25 |
Errors by subgroup
| Subgroup | Mapping | Adjusted error (¢) |
|---|---|---|
| 2.3 | [⟨15 24]] | 8.979801 |
| 2.5 | [⟨15 35]] | 6.826357 |
| 2.7 | [⟨15 42]] | 4.418738 |
| 2.11 | [⟨15 52]] | 4.336492 |
| 2.3.5 |
[⟨15 24 35]] |
10.742841 |
| 2.3.7 | [⟨15 24 42]] | 17.481581 |
| 2.3.11 |
[⟨15 24 52]] |
16.831238 |
| 2.5.7 | [⟨15 35 42]] | 10.509269 |
| 2.5.11 | [⟨15 35 52]] | 8.335693 |
| 2.7.11 | [⟨15 42 52]] | 8.002641 |
| 2.3.5.7 | [⟨15 24 35 42]] | 15.603114 |
| 2.3.5.11 | [⟨15 24 35 52]] | 14.693746 |
| 2.3.7.11 | [⟨15 24 42 52]] | 18.660367 |
| 2.5.7.11 | [⟨15 35 42 52]] | 11.462127 |
| 2.3.5.7.11 | [⟨15 24 35 42 52]] | 17.258371 |
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 14.7826 | 14.8268 | 15bcef | ⟨15 23 34 42 51 55] |
| 14.8268 | 14.8583 | 15cef | ⟨15 24 34 42 51 55] |
| 14.8583 | 14.8868 | 15ef | ⟨15 24 35 42 51 55] |
| 14.8868 | 14.9982 | 15f | ⟨15 24 35 42 52 55] |
| 14.9982 | 15.1388 | 15 | ⟨15 24 35 42 52 56] |
| 15.1388 | 15.1759 | 15d | ⟨15 24 35 43 52 56] |
| 15.1759 | 15.2685 | 15dee | ⟨15 24 35 43 53 56] |
Rank-2 temperaments
| Periods per 8ve |
Generator | Associated ratio |
Temperaments | Mos scales |
|---|---|---|---|---|
| 1 | 1\15 | 21/20 | Nautilus Valentine |
|
| 1 | 2\15 | 11/10 | Porcupine / opossum | 1L 6s, 7L 1s |
| 1 | 4\15 | 6/5 77/64 |
Cata / keemun / catalan Orgone / superkleismic |
3L 1s, 4L 3s, 4L 7s |
| 1 | 7\15 | 7/5 | Progress Parakangaroo |
2L 1s, 2L 3s, 2L 5s, 2L 7s 2L 9s, 2L 11s |
| 3 | 1\15 | 16/15 | Augmented / augene | 3L 3s, 3L 6s, 3L 9s |
| 3 | 2\15 | 7/6 | Triforce | 3L 3s, 6L 3s |
| 5 | 1\15 | 16/15 | Blackwood / blacksmith | 5L 5s |
Commas
15et tempers out the following commas using the patent val ⟨15 24 35 42 52 56].
| Prime limit |
Ratio[1] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | 256/243 | [8 -5⟩ | 90.225 | Sawa | Blackwood comma, Pythagorean limma |
| 5 | (18 digits) | [20 5 -12⟩ | 74.01 | Saquadtrigu | Hypovishnuzma |
| 5 | 250/243 | [1 -5 3⟩ | 49.166 | Triyo | Porcupine comma, maximal |
| 5 | 128/125 | [7 0 -3⟩ | 41.059 | Trigu | Augmented comma, lesser diesis |
| 5 | 15625/15552 | [-6 -5 6⟩ | 8.107 | Tribiyo | Kleisma |
| 7 | 28/27 | [2 -3 0 1⟩ | 62.961 | Zo | Septimal third-tone, trienstonic comma |
| 7 | 1029/1000 | [-3 1 -3 3⟩ | 49.492 | Trizogu | Keega |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.697 | Zozo | Semaphoresma, Slendro diesis |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.264 | Ru | Archytas' comma, septimal comma |
| 7 | 64827/64000 | [-9 3 -3 4⟩ | 22.227 | Laquadzo-atrigu | Squalentine comma |
| 7 | [-5 -3 3 1⟩ | 21.902 | Zotriyo | Keema | |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.795 | Zotrigu | Starling comma |
| 7 | 4000/3969 |
[5 -4 3 -2⟩ |
13.469 | Rurutriyo | Octagar comma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.433 | Latrizo | Gamelisma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.362 | Saruru-atrigu | Porwell comma |
| 7 | (12 digits) | [-4 6 -6 3⟩ | 0.325 | Trizogugu | Landscape comma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.399 | Luyoyo | Ptolemisma |
| 11 | 121/120 |
[-3 -1 -1 0 2⟩ |
14.367 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.865 | Lorugugu | Valinorsma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.394 | Satrilu-aruru | Orgonisma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.503 | Lozoyo | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.930 | Luzozogu | Werckisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.032 | Triluyo | Wizardharry |
| 11 | [-4 -3 2 -1 2⟩ | 0.572 | Loloruyoyo | Lehmerisma | |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.130 | Thozogu | Superleap comma, biome comma |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.563 | Bithogu | Island comma |
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Scales
Some scales commonly used in 15edo, written in a common mode, in steps of 15edo:
MOS scales
- Augene[6] 3L 3s (period = 5\15, gen = 1\15): 4 1 4 1 4 1
- Augene[9] 3L 6s (period = 5\15, gen = 1\15): 3 1 1 3 1 1 3 1 1
- Augene[12] 3L 9s (period = 5\15, gen = 1\15): 2 1 1 1 2 1 1 1 2 1 1 1
- Triforce[6] 3L 3s (period = 5\15, gen = 2\15): 3 2 3 2 3 2
- Triforce[9] 6L 3s (period = 5\15, gen = 2\15): 2 1 2 2 1 2 2 1 2
- Porcupine[7] 1L 6s (gen = 2\15): 3 2 2 2 2 2 2
- Porcupine[8] 7L 1s (gen = 2\15): 2 1 2 2 2 2 2 2
- Hanson/Keemun/Orgone[7] 4L 3s (gen = 4\15): 1 3 1 3 1 3 3
- Hanson/Keemun/Orgone[11] 4L 7s (gen = 4\15): 1 2 1 1 2 1 1 2 1 2 1
- Blackwood[10] 5L 5s (period = 3\15, gen = 1\15): 2 1 2 1 2 1 2 1 2 1 (Blackwood Decatonic)
Blackwood decatonic, major mode, in 15edo
Other scales
- Zarlino/Ptolemy diatonic, "just" major (Porcupine[7] 6|0 b4 #7): 3 2 1 3 2 3 1
- inverse of Zarlino/Ptolemy diatonic, natural minor (Porcupine[7] 3|3 #2 b6): 3 1 2 3 1 3 2
- tetrachordal major: 3 2 1 3 3 2 1
- inverse of tetrachordal major, tetrachordal minor: 3 1 2 3 1 2 3
- "just"/Pinetone major pentatonic (subset of Porcupine[7]): 3 2 4 2 4
- "just"/Pinetone minor pentatonic (inverse of "just" major pentatonic, subset of Porcupine[7]): 4 2 3 4 2
- Porcupine bright major #7 (Porcupine harmonic major) - Porcupine[7] 6|0 #7: 3 2 2 2 2 3 1
- Porcupine bright major #6 #7 (Porcupine melodic major) - Porcupine[7] 6|0 #7: 3 2 2 2 3 2 1
- Porcupine bright minor #2 (Porcupine harmonic minor) - Porcupine[7] 4|2 #2: 3 1 3 2 2 2 2 (mode of bright major #7)
- Porcupine dark minor #2 (Porcupine melodic minor) - Porcupine[7] 3|3 #2: 3 1 2 3 2 2 2 (inverse of bright major #6 #7)
- Porcupine bright harmonic 11th mode - Porcupine[7] 6|0 b7: 3 2 2 2 2 1 3
- Pinetone diminished octatonic / Porcupine[8] bright minor #2 - Porcupine[8] 2|5 #5: 2 2 1 3 1 2 2 2
- "just" harmonic minor: 3 1 2 3 1 4 1
- "just" harmonic major: 3 2 1 3 1 4 1
- "just" melodic minor ascending: 3 1 2 3 2 3 1
- Marvel double harmonic hexatonic (Augene[6] 4M): 1 4 1 4 4 1, 1 4 4 1 4 1
- Marvel double harmonic major: 1 4 1 3 1 4 1
- Marvel double harmonic nonatonic (Augene[9] 4M): 1 3 1 1 3 1 3 1 1, 1 1 3 1 3 1 1 3 1
- Marvel double harmonic decatonic: 1 3 1 1 2 1 1 3 1 1
- enharmonic trichord octave species: 1 5 3 1 5 , 5 1 3 5 1
- chromatic tetrachord octave species: 1 1 4 3 1 1 4, 4 1 1 3 4 1 1, 1 4 1 3 1 4 1
- Chopsticks double octave scale: 4 2 4 2 4 2 4 2 4 2
- 5- to 10-tone scales in 47zpi (slightly stretched 15edo)
Horagrams
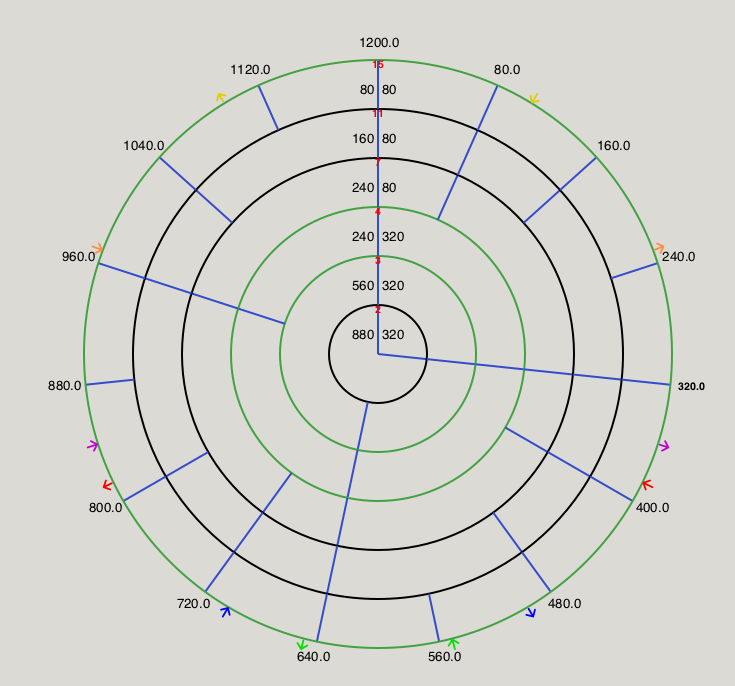
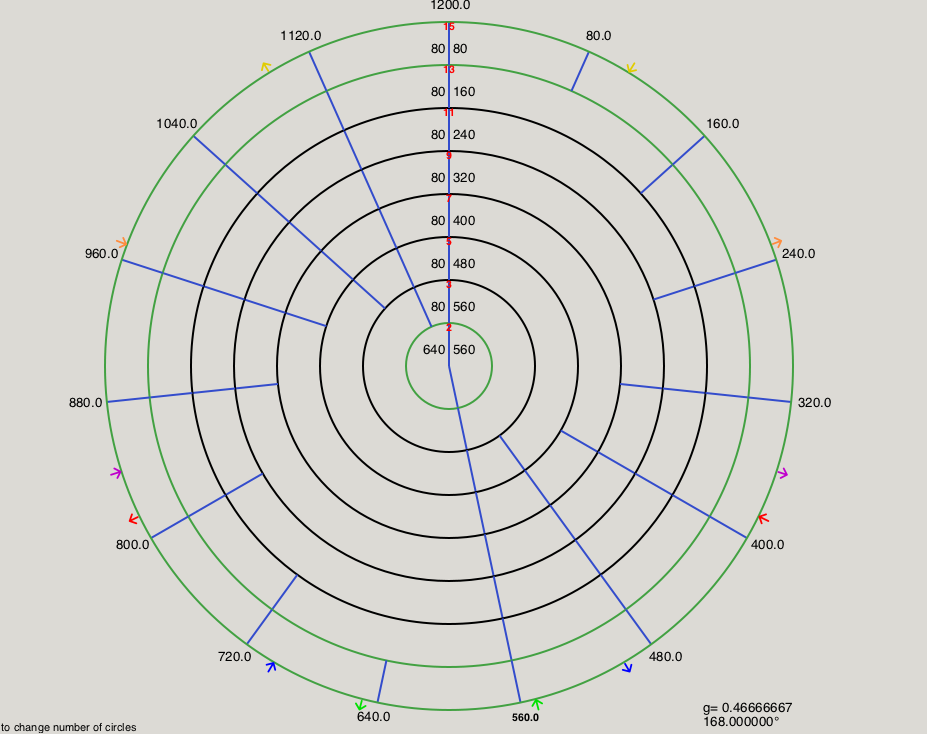
Diagrams
Keyboard
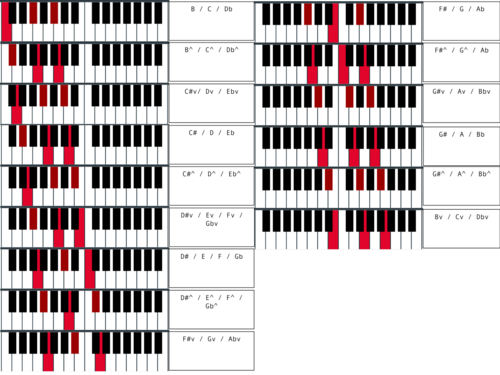
Lumatone
See Lumatone mapping for 15edo
Music
- See also: Category:15edo tracks
- XA 15-ET Directory
Other info
Keyboard layouts
-
Porcupine layout for 15edo
-
Hanson layout for 15edo
-
Zarlino layout for 15edo
Further reading
Theory
- Carson, Brent. Fifteen Note Equal Temperment
- Darreg, Ivor. 15-Tone Scale System. 1991. (Originally at [1], now broken)
- InTeAS. The Pentadecaphonic System (2001, archived)
Guitar
- Sword, Ron. Pentadecaphonic Scales for Guitar: Scales, Chord-Scales, Notation, and Theory for Fifteen Equal Divisions of the Octave. (A large repository of all known scales and temperament families in the 15edo system. 300+ examples with chord-scale progressions.)
Notes
- ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.