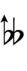20edo

← 19edo

20edo

21edo →

Prime factorization

2² × 5

Step size

60¢

Fifth

12\20 (720¢) (→3\5)

Semitones (A1:m2)

4:0 (240¢ : 0¢)

Consistency limit

3

Distinct consistency limit

3

20 equal divisions of the octave (abbreviated 20edo or 20ed2), also called 20-tone equal temperament (20tet) or 20 equal temperament (20et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 20 equal parts of exactly 60 ¢ each. Each step represents a frequency ratio of 2^1/20, or the 20th root of 2.

Theory

20edo contains smaller EDOs: 2, 4, 5, and 10 and is part of the 5n family of equal divisions of the octave. It fairly approximates the harmonics 7 (from 5edo), 11, 13 & 15 (from 10edo), 19 & 27 (from 4edo), 29 and 31; as well as the other harmonics more loosely (though to some people, still functionally) approximated. Thus, 20-EDO does a reasonably convincing approximation of harmonics 4:7:11:13:15.

As 7, 11, & 15 are all flat by approximately 10 cents, their flatness cancels out when combined in composite ratios, making an 11:14:15 chord (0-7-9 steps) and its utonal inversion particularly precise. Using 9/20 as the generator and treating these as the primary major and minor triads produces Balzano nonatonic and undecatonic scales, which is probably the clearest arrangement for the black/white keys on a 20 tone keyboard.

Treating the generator as 11\20 creates the same scale, but the primary triads are now 13:16:19 (0-6-11 steps) and its inversion instead. The 11\20 generator is a near-optimal tuning for both Mavericks temperament (which has a ~19/13 generator) and Score temperament (which has a ~16/11 generator).

Alternately, 20edo can be used as a tuning of the blackwood temperament, combining minor and major thirds to generate a highly symmetrical decatonic scale where every note is root to a major or minor triad and 7-limit tetrad that are heavily tempered, but in a useful way, as you can easily modulate to anywhere in the small cycle of 5ths, and build extended chords that use every note in the scale without clashing. Either of these works better than trying to force 20 into a diatonic framework.

20edo also possesses a 6L 1s scale generated using the narrow major second of 3\20 that is probably best interpreted as the sharp extreme of tetracot temperament and a 3L 5s generated by 7/20 that functions as the flat end of squares.

Thanks to its sevenths, 20edo is an ideal tuning for its size for metallic harmony.

Odd harmonics

Approximation of odd harmonics in 20edo
Harmonic		3	5	7	9	11	13	15	17	19	21	23
Error	Absolute (¢)	+18.0	-26.3	-8.8	-23.9	-11.3	-0.5	-8.3	+15.0	+2.5	+9.2	-28.3
Error	Relative (%)	+30.1	-43.9	-14.7	-39.9	-18.9	-0.9	-13.8	+25.1	+4.1	+15.4	-47.1
Steps (reduced)		32 (12)	46 (6)	56 (16)	63 (3)	69 (9)	74 (14)	78 (18)	82 (2)	85 (5)	88 (8)	90 (10)

Intervals

Like 15edo, every note has many names. D is also C# and Eb. The major 3rd is also a perfect 4th and a dim 5th.

Degree	Cents	Approximate Ratios	Ups and Downs Notation			Balzano Notation	Archeotonic notation	Nearest Harmonic
0	0	1/1	unison	P1	D	1	D	1
1	60	29/28	up unison, upminor 2nd	^1, ^m2	^D, ^Eb	1#/2b	D#	33
2	120	15/14, 14/13	dup unison, mid 2nd	^^1, ~2	^^D, vvE	2	Eb	69
3	180	10/9	downmajor 2nd	vM2	vE	2#/3b	E	71
4	240	8/7, 15/13	major 2nd, minor 3rd	M2, m3	E, F	3	E#	37
5	300	13/11, 19/16	upminor 3rd	^m3	^F	3#/4b	Fb	19
6	360	16/13, 5/4	mid 3rd	~3	^^F, vvF#	4	F	79
7	420	14/11, 51/40	downmajor 3rd	vM3	vF#	4#	F#	41
8	480	25/19, 4/3	major 3rd, perfect fourth	M3, P4	F#, G	5b	Gb	21
9	540	15/11, 11/8	up-fourth	^4	^G	5	G	11
10	600	7/5	mid fourth, mid fifth	~4, ~5	^^G, vvA	5#/6b	G#/Ab	91
11	660	22/15, 16/11	down-fifth	v5	vA	6	A	47
12	720	38/25, 3/2	fifth	P5, m6	A	6#/7b	A#	97
13	780	11/7, 25/16	upfifth, upminor 6th	^5, ^m6	^A, ^Bb	7	Bb	25
14	840	13/8, 8/5	mid 6th	~6	^^A, vvB	7#/8b	B	13
15	900	22/13, 32/19	downmajor 6th	vM6	vB	8	B#	27
16	960	7/4, 26/15	major 6th, minor 7th	M6, m7	B, C	8#/9b	Cb	7
17	1020	9/5	upminor 7th	^m7	^C	9	C	115
18	1080	28/15, 15/8, 13/7	mid 7th	~7	^^C, vvD	9#	C#	15
19	1140	56/29	downmajor 7th	vM7	vD	1b	Db	31
20	1200	2/1	octave	P8	D	1	D	2

Selected 19-limit just intervals

Direct approximation (even if inconsistent)
Interval, complement	Error (abs, ¢)
16/13 13/8	0.5276
15/14 28/15	0.5571
10/9 9/5	2.4037
19/16 32/19	2.4869
14/11 11/7	2.4920
19/13 26/19	3.0146
15/11 22/15	3.0492
15/13 26/15	7.7410
16/15 15/8	8.2687
14/13 13/7	8.2982
8/7 7/4	8.8259
13/11 22/13	10.7902
11/8 16/11	11.3179
11/9 18/11	12.5920
11/10 20/11	14.9957
17/16 32/17	15.0445
9/7 14/9	15.0840
6/5 5/3	15.6412
7/5 10/7	17.4878
3/2 4/3	18.0449
13/12 24/13	18.5726
9/8 16/9	23.9100
5/4 8/5	26.3137
7/6 12/7	26.8709
12/11 11/6	29.36294

Chord names

20edo chords can be named using ups and downs. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).

0-4-12 = D E A = Dsus2 = "D sus 2", or D F A = Dm = "D minor"
0-5-12 = D ^F A = D^m = "D upminor"
0-6-12 = D ^^F A = D~ = "D mid"
0-7-12 = D vF# A = Dv = "D down" or "D downmajor"
0-8-12 = D G A = Dsus4, or D F# A = D = "D" or "D major"
0-4-12-16 = D F A C = Dm7 = "D minor seven", or D F A B = Dm6 = "D minor six"
0-5-12-16 = D ^F A C = D^m,7 = "D upminor add-seven", or D ^F A B = D^m,6 = "D upminor add-six"
0-6-12-16 = D ^^F A C = D~,7 = "D mid add-seven", or D ^^F A B = D~,6 = "D mid add-six"
0-7-12-16 = D vF# A C = Dv,7 = "D down add-seven", or D vF# A B = Dv,6 = "D down add-six"
0-8-12-16 = D F# A C = D7 = "D seven", or D F# A B = D6 = "D six"
0-7-12-19 = D vF# A vC# = DvM7 = "D downmajor seven"
0-5-12-17 = D ^F A ^C = D^m7 = "D upminor-seven", or D ^F A ^B = D^m6 = "D upminor-six"

For a more complete list, see Ups and Downs Notation - Chords and Chord Progressions. Because many intervals have several names, many chords do too.

Modes

20 tone equal modes:

3 1 3 1 3 1 3 1 3 1	Blackwood Major Decatonic (bi-equal decatonic, according to the MOS naming scheme)
1 3 1 3 1 3 1 3 1 3	Blackwood Minor Decatonic (also bi-equal decatonic)
2 1 1 2 1 1 2 1 1 2 1 1	Blackwood Major Pentadecatonic (also tri-equal pentadecatonic)
1 1 2 1 1 2 1 1 2 1 1 2	Blackwood Diminished Pentadecatonic (also tri-equal pentadecatonic)
1 2 1 1 2 1 1 2 1 1 2 1	Blackwood Minor Pentadecatonic (also tri-equal pentadecatonic)
2 3 2 2 2 3 2 2 2	Balzano Nine-tone (fair mavila, score9) ^[1]
2 2 2 2 1 2 2 2 2 2 1	Balzano Eleven-tone, Agmon Diatonic DS4, score11
2 2 2 3 2 2 2 3 2	Balzano Nine-tone inverse (also fair mavila, score9)
1 2 2 2 2 2 1 2 2 2 2	Balzano Eleven-tone inverse (also score11)
2 3 2 3 2 3 2 3	Octatonic (diminished, according to the MOS naming scheme)
3 2 3 2 3 2 3 2	Diminished
2 2 1 2 2 1 2 2 1 2 2 1	Dodecatonic
2 1 2 2 1 2 2 1 2 2 1 2	Diminished
1 2 2 1 2 2 1 2 2 1 2 2	Diminished
4 3 1 4 3 4 1	Twenty-tone "Major"
4 1 3 4 1 4 3	Twenty-tone "Minor"
2 2 1 2 1 2 2 1 2 2 2 1	Twelve-tone Chromatic
2 2 2 2 1 2 2 2 2 1 2	Zweifel Major
2 1 2 2 2 2 2 1 2 2 2	Zweifel Natural Minor
3 3 3 3 3 3 2	Major quasi-equal Heptatonic (archaeotonic or Grumpy heptatonic)
3 2 3 3 3 3 3	Minor quasi-equal Heptatonic (also archaeotonic)
2 2 1 2 1 2 1 2 1 2 1 2 1	Major quasi-equal Triskaidecatonic (Grumpy triskaidecatonic)
2 1 2 1 2 1 2 1 2 1 2 1 2	Minor quasi-equal Triskaidecatonic A
1 2 1 2 1 2 1 2 1 2 1 2 2	Minor quasi-equal Triskaidecatonic B
2 1 2 1 2 1 2 1 2 1 2 2 1	Minor quasi-equal Triskaidecatonic C
3 2 2 2 2 3 2 2 2	Rothenberg Generalized Diatonic (also balzano or score9)
3 4 1 4 3 3 2	Stearns Major
7 2 7 2 2	score5 pentic, classic pentatonic
5 2 2 5 2 2 2	score7 (mavila, anti-diatonic)

↑ Generalized Diatonic and Pentatonic Scales: A Group-Theoretic Approach

Regular temperament properties

Uniform maps

13-limit uniform maps between 19.5 and 20.5
Min. size	Max. size	Wart notation	Map
19.5000	19.5119	20bccddeeeeffff	⟨20 31 45 55 67 72]
19.5119	19.5923	20bccddeeffff	⟨20 31 45 55 68 72]
19.5923	19.5958	20bccddeeff	⟨20 31 45 55 68 73]
19.5958	19.7695	20bddeeff	⟨20 31 46 55 68 73]
19.7695	19.8009	20beeff	⟨20 31 46 56 68 73]
19.8009	19.8625	20bff	⟨20 31 46 56 69 73]
19.8625	19.8743	20b	⟨20 31 46 56 69 74]
19.8743	20.0265	20	⟨20 32 46 56 69 74]
20.0265	20.0900	20c	⟨20 32 47 56 69 74]
20.0900	20.1257	20ce	⟨20 32 47 56 70 74]
20.1257	20.1327	20cde	⟨20 32 47 57 70 74]
20.1327	20.3791	20cdef	⟨20 32 47 57 70 75]
20.3791	20.4030	20cdeeef	⟨20 32 47 57 71 75]
20.4030	20.4571	20cdeeefff	⟨20 32 47 57 71 76]
20.4571	20.4819	20cccdeeefff	⟨20 32 48 57 71 76]
20.4819	20.5000	20cccdddeeefff	⟨20 32 48 58 71 76]

Commas

20 EDO tempers out the following commas. (Note: This assumes the val ⟨20 32 46 56 69 74].)

Prime Limit	Ratio^[1]	Monzo	Cents	Color name	Name(s)
3	256/243	[8 -5⟩	90.22	Sawa	Limma, Pythagorean Minor 2nd
5	16875/16384	[-14 3 4⟩	51.12	Laquadyo	Negri Comma, Double Augmentation Diesis
5	(16 digits)	[-25 7 6⟩	31.57	Lala-tribiyo	Ampersand, Ampersand's Comma
5	2048/2025	[11 -4 -2⟩	19.55	Sagugu	Diaschisma
7	525/512	[-9 1 2 1⟩	43.41	Lazoyoyo	Avicennma, Avicenna's Enharmonic Diesis
7	49/48	[-4 -1 0 2⟩	35.70	Zozo	Slendro Diesis
7	50/49	[1 0 2 -2⟩	34.98	Biruyo	Tritonic Diesis, Jubilisma
7	686/675	[1 -3 -2 3⟩	27.99	Trizo-agugu	Senga
7	64/63	[6 -2 0 -1⟩	27.26	Ru	Septimal Comma, Archytas' Comma, Leipziger Komma
7	(18 digits)	[-10 7 8 -7⟩	22.41	Lasepru-aquadbiyo	Blackjackisma
7	1029/1024	[-10 1 0 3⟩	8.43	Latrizo	Gamelisma
7	225/224	[-5 2 2 -1⟩	7.71	Ruyoyo	Septimal Kleisma, Marvel Comma
7	16875/16807	[0 3 4 -5⟩	6.99	Quinru-aquadyo	Mirkwai
7	(24 digits)	[11 -10 -10 10⟩	5.57	Saquinbizogu	Linus
7	2401/2400	[-5 -1 -2 4⟩	0.72	Bizozogu	Breedsma
11	121/120	[-3 -1 -1 0 2⟩	14.37	Lologu	Biyatisma
13	91/90	[-1 -2 -1 1 0 1⟩	19.13	Thozogu	Superleap
13	676/675	[2 -3 -2 0 0 2⟩	2.56	Bithogu	Parizeksma

↑ Ratios longer than 10 digits are presented by placeholders with informative hints

Instruments

Like other members of the 5EDO family, 20-EDO lends itself well to guitar (and other fretted string instruments), on account of the fact that five of its flat 4ths (at 480 cents) exactly spans two octaves (480*5=2400), meaning the open strings can be uniformly tuned in 4ths. This allows for greater uniformity in chord and scale fingering patterns than in 12-TET, making it exceptionally easy to learn. For instance, the fingering for an "E" chord would be 0-4-4-2-0-0 (low to high), an "A" chord would be 0-0-4-4-2-0, and a "D" chord would be 2-0-0-4-4-2.
Lumatone mapping for 20edo