52edo
| ← 51edo | 52edo | 53edo → |
52 equal divisions of the octave (abbreviated 52edo or 52ed2), also called 52-tone equal temperament (52tet) or 52 equal temperament (52et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 52 equal parts of about 23.1 ¢ each. Each step represents a frequency ratio of 21/52, or the 52nd root of 2.
Theory
52edo has 26edo's very flat meantone fifth and a very sharp fifth close to 1/2-septimal-comma superpyth. The patent val has the same mapping for 3, 7, 11 and 13 as 26 does, but its 5 is sharp rather than flat. From this it tempers out 648/625 rather than 81/80 in the 5-limit, and 225/224 and 1029/1024 in the 7-limit, showing it supports miracle, albeit badly, and may be defined by the tempering out of both 648/625 and miracle. In the 11-limit it tempers out 99/98 and 176/175 and in the 13-limit 78/77, 144/143 and 169/168. It supplies the optimal patent val for then 12 & 40 temperament of the diminished family in the 7- and 11-limit, and also in the 13-limit where it can be defined as tempering out 78/77, 99/98, 176/175, 567/550 rather than by two patent vals. It also gives the 13-limit patent val for the 21 & 52 variant of miracle.
Using the sharp fifth rather than the flat fifth (that is, using the 52b val), it contains a version of porcupine temperament, and combining 30\52 with 31\52 leads to a whole tone of 9\52, or 208 cents, which can be used inconsistently.
The 5\52 interval approximates 31/29 well, and when used as a generator produces tricesimoprimal miracloid temperament. The relationship is also preserved exactly in the period-52 french deck temperament.
The 11\52 (253.846 ¢) semifourth is a very accurate 22/19, with an error of only +0.041 ¢ and a closing error of only 9.3%.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -9.6 | +6.0 | +0.4 | +3.8 | +2.5 | -9.8 | -3.7 | +10.4 | +2.5 | -9.2 | -5.2 |
| Relative (%) | -41.8 | +26.0 | +1.8 | +16.4 | +11.0 | -42.3 | -15.8 | +45.2 | +10.8 | -40.1 | -22.5 | |
| Steps (reduced) |
82 (30) |
121 (17) |
146 (42) |
165 (9) |
180 (24) |
192 (36) |
203 (47) |
213 (5) |
221 (13) |
228 (20) |
235 (27) | |
Subsets and supersets
Since 52 factors into 22 × 13, 52edo contains subset edos 2, 4, 13, and 26.
Intervals
| Degrees | Centss | Ups and downs notation | ||
|---|---|---|---|---|
| 0 | 0.000 | Perfect 1sn | P1 | D |
| 1 | 23.077 | Up 1sn | ^1 | ^D |
| 2 | 46.154 | Aug 1sn | A1 | D# |
| 3 | 69.231 | Downdim 2nd, Upaug 1sn | vd2, ^A1 | vEbb, ^D# |
| 4 | 92.308 | Dim 2nd | d2 | Ebb |
| 5 | 115.358 | Downminor 2nd | vm2 | vEb |
| 6 | 138.462 | Minor 2nd | m2 | Eb |
| 7 | 161.538 | Mid 2nd | ~2 | vE, ^Eb |
| 8 | 184.615 | Major 2nd | M2 | E |
| 9 | 207.692 | Upmajor 2nd | ^M2 | ^E |
| 10 | 230.769 | Aug 2nd | A2 | E# |
| 11 | 253.846 | Downdim 3rd, Upaug 2nd | vd3, ^A2 | vFb, ^E# |
| 12 | 276.923 | Dim 3rd | d3 | Fb |
| 13 | 300.000 | Downminor 3rd | vm3 | vF |
| 14 | 323.077 | Minor 3rd | m3 | F |
| 15 | 346.154 | Mid 3rd | ~3 | ^F, vF# |
| 16 | 369.231 | Major 3rd | M3 | F# |
| 17 | 392.308 | Upmajor 3rd | ^M3 | ^F# |
| 18 | 415.385 | Aug 3rd | A3 | Fx |
| 19 | 438.462 | Downdim 4th, Upaug 3rd | vd4, ^A4 | vGb, ^Fx |
| 20 | 461.538 | Dim 4th | d4 | Gb |
| 21 | 484.615 | Down 4th | v4 | vG |
| 22 | 507.692 | Perfect 4th | P4 | G |
| 23 | 530.769 | Up 4th | ^4 | ^G |
| 24 | 553.846 | Aug 4th | A4 | G# |
| 25 | 576.293 | Upaug 4th | ^A4 | ^G# |
| 26 | 600.000 | Double-aug 4th, Double-dim 5th | AA4, dd5 | Gx, Abb |
| 27 | 623.077 | Downdim 5th | vd5 | vAb |
| 28 | 646.154 | Dim 5th | d5 | Ab |
| 29 | 669.231 | Down 5th | v5 | vA |
| 30 | 692.308 | Perfect 5th | P5 | A |
| 31 | 715.385 | Up 5th | ^5 | ^A |
| 32 | 738.462 | Aug 5th | A5 | A# |
| 33 | 761.538 | Downdim 6th, Upaug 5th | vd6, ^A5 | vBbb, ^A# |
| 34 | 784.615 | Dim 6th | d6 | Bbb |
| 35 | 807.692 | Downminor 6th | vm6 | vBb |
| 36 | 830.769 | Minor 6th | m6 | Bb |
| 37 | 853.846 | Mid 6th | ~6 | vB, ^Bb |
| 38 | 876.923 | Major 6th | M6 | B |
| 39 | 900.000 | Upmajor 6th | ^M6 | ^B |
| 40 | 923.077 | Aug 6th | A6 | B# |
| 41 | 946.154 | Downdim 7th, Upaug 6th | vd7, ^A6 | vCb, ^B# |
| 42 | 969.231 | Dim 7th | d7 | Cb |
| 43 | 992.308 | Downminor 7th | vm7 | vC |
| 44 | 1015.385 | Minor 7th | m7 | C |
| 45 | 1038.462 | Mid 7th | ~7 | ^C, vC# |
| 46 | 1061.538 | Major 7th | M7 | C# |
| 47 | 1084.615 | Upmajor 7th | ^M7 | ^C# |
| 48 | 1107.692 | Aug 7th | A7 | Cx |
| 49 | 1130.769 | Downdim 8ve, Upaug 7th | vd8, ^A7 | vDb, ^Cx |
| 50 | 1153.846 | Dim 8ve | d8 | Db |
| 51 | 1176.923 | Down 8ve | v8 | vD |
| 52 | 1200.000 | Perfect 8ve | P8 | D |
Notation
13edo notation can be used together with +/- eighth-tone accidentals.
Ups and downs notation
Using Helmholtz–Ellis accidentals, 52edo can also be notated using ups and downs notation or Stein–Zimmerman quarter tone accidentals:
| Step offset | −4 | −3 | −2 | −1 | 0 | +1 | +2 | +3 | +4 |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
|
|
|
|
| Step offset | −4 | −3 | −2 | −1 | 0 | +1 | +2 | +3 | +4 |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
|
|
|
|
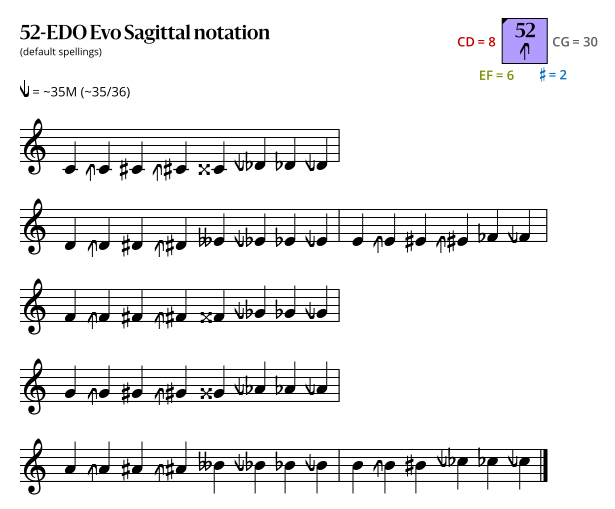
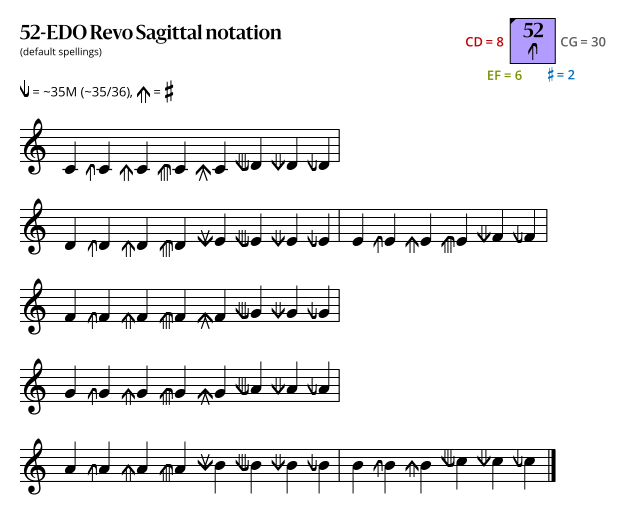
Sagittal notation
This notation uses the same sagittal sequence as EDOs 45 and 59b, and is a superset of the notations for EDOs 26 and 13.
Evo flavor
Revo flavor
Evo-SZ flavor
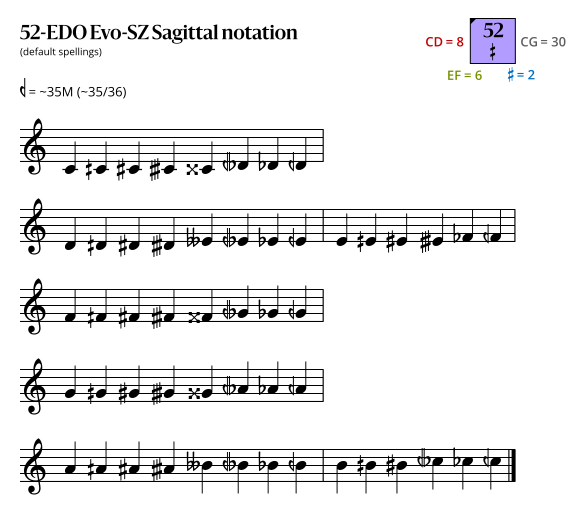
Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is also a Stein-Zimmerman notation.
Instruments
Lumatone
See Lumatone mapping for 52edo
Music
- microtonal improvisation in 52edo (2025)
- Waltz in 52edo (2025)