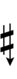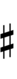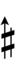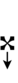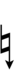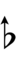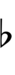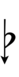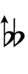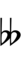57edo
| ← 56edo | 57edo | 58edo → |
57 equal divisions of the octave (abbreviated 57edo or 57ed2), also called 57-tone equal temperament (57tet) or 57 equal temperament (57et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 57 equal parts of about 21.1 ¢ each. Each step represents a frequency ratio of 21/57, or the 57th root of 2.
Theory
57edo is an excellent tuning for the 2.5/3.7.11.13.17.19 just intonation subgroup. One way to describe 57edo is that it has a 5-limit part consisting of three rings of 19edo, plus a no-threes no-fives part which is much more accurate.
Using the full prime-limit patent val, the equal temperament tempers out 81/80, 1029/1024, and 3125/3072 in the 7-limit; and 99/98, 385/384, 441/440, and 625/616 in the 11-limit. A good generator to exploit the 2.5/3.7.11.13.17.19 aspect of 57 is the approximate 11/8, which is 26\57. This gives the 19-limit 46 & 57 temperament heinz. It can also be used to tune mothra as well as trismegistus.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -7.22 | -7.37 | -0.40 | +6.62 | -3.95 | +1.58 | +6.47 | +0.31 | -2.78 | -7.62 | +3.30 |
| Relative (%) | -34.3 | -35.0 | -1.9 | +31.4 | -18.8 | +7.5 | +30.7 | +1.5 | -13.2 | -36.2 | +15.7 | |
| Steps (reduced) |
90 (33) |
132 (18) |
160 (46) |
181 (10) |
197 (26) |
211 (40) |
223 (52) |
233 (5) |
242 (14) |
250 (22) |
258 (30) | |
Subsets and supersets
57edo contains 3edo and 19edo as subsets.
Intervals
| # | Cents | Ups and downs notation (Flat Fifth 11\19) |
Ups and downs notation (Sharp Fifth 34\57) |
|---|---|---|---|
| 0 | 0.00 | D | D |
| 1 | 21.05 | ^D, ^E♭♭♭ | ^D, E♭ |
| 2 | 42.11 | vD♯, vE♭♭ | ^^D, ^E♭ |
| 3 | 63.16 | D♯, E♭♭ | ^3D, ^^E♭ |
| 4 | 84.21 | ^D♯, ^E♭♭ | ^4D, ^3E♭ |
| 5 | 105.26 | vD𝄪, vE♭ | ^5D, ^4E♭ |
| 6 | 126.32 | D𝄪, E♭ | v4D♯, v5E |
| 7 | 147.37 | ^D𝄪, ^E♭ | v3D♯, v4E |
| 8 | 168.42 | vD♯𝄪, vE | vvD♯, v3E |
| 9 | 189.47 | E | vD♯, vvE |
| 10 | 210.53 | ^E, ^F♭♭ | D♯, vE |
| 11 | 231.58 | vE♯, vF♭ | E |
| 12 | 252.63 | E♯, F♭ | F |
| 13 | 273.68 | ^E♯, ^F♭ | ^F, G♭ |
| 14 | 294.74 | vE𝄪, vF | ^^F, ^G♭ |
| 15 | 315.79 | F | ^3F, ^^G♭ |
| 16 | 336.84 | ^F, ^G♭♭♭ | ^4F, ^3G♭ |
| 17 | 357.89 | vF♯, vG♭♭ | ^5F, ^4G♭ |
| 18 | 378.95 | F♯, G♭♭ | v4F♯, v5G |
| 19 | 400.00 | ^F♯, ^G♭♭ | v3F♯, v4G |
| 20 | 421.05 | vF𝄪, vG♭ | vvF♯, v3G |
| 21 | 442.11 | F𝄪, G♭ | vF♯, vvG |
| 22 | 463.16 | ^F𝄪, ^G♭ | F♯, vG |
| 23 | 484.21 | vF♯𝄪, vG | G |
| 24 | 505.26 | G | ^G, A♭ |
| 25 | 526.32 | ^G, ^A♭♭♭ | ^^G, ^A♭ |
| 26 | 547.37 | vG♯, vA♭♭ | ^3G, ^^A♭ |
| 27 | 568.42 | G♯, A♭♭ | ^4G, ^3A♭ |
| 28 | 589.47 | ^G♯, ^A♭♭ | ^5G, ^4A♭ |
| 29 | 610.53 | vG𝄪, vA♭ | v4G♯, v5A |
| 30 | 631.58 | G𝄪, A♭ | v3G♯, v4A |
| 31 | 652.63 | ^G𝄪, ^A♭ | vvG♯, v3A |
| 32 | 673.68 | vG♯𝄪, vA | vG♯, vvA |
| 33 | 694.74 | A | G♯, vA |
| 34 | 715.79 | ^A, ^B♭♭♭ | A |
| 35 | 736.84 | vA♯, vB♭♭ | ^A, B♭ |
| 36 | 757.89 | A♯, B♭♭ | ^^A, ^B♭ |
| 37 | 778.95 | ^A♯, ^B♭♭ | ^3A, ^^B♭ |
| 38 | 800.00 | vA𝄪, vB♭ | ^4A, ^3B♭ |
| 39 | 821.05 | A𝄪, B♭ | ^5A, ^4B♭ |
| 40 | 842.11 | ^A𝄪, ^B♭ | v4A♯, v5B |
| 41 | 863.16 | vA♯𝄪, vB | v3A♯, v4B |
| 42 | 884.21 | B | vvA♯, v3B |
| 43 | 905.26 | ^B, ^C♭♭ | vA♯, vvB |
| 44 | 926.32 | vB♯, vC♭ | A♯, vB |
| 45 | 947.37 | B♯, C♭ | B |
| 46 | 968.42 | ^B♯, ^C♭ | C |
| 47 | 989.47 | vB𝄪, vC | ^C, D♭ |
| 48 | 1010.53 | C | ^^C, ^D♭ |
| 49 | 1031.58 | ^C, ^D♭♭♭ | ^3C, ^^D♭ |
| 50 | 1052.63 | vC♯, vD♭♭ | ^4C, ^3D♭ |
| 51 | 1073.68 | C♯, D♭♭ | ^5C, ^4D♭ |
| 52 | 1094.74 | ^C♯, ^D♭♭ | v4C♯, v5D |
| 53 | 1115.79 | vC𝄪, vD♭ | v3C♯, v4D |
| 54 | 1136.84 | C𝄪, D♭ | vvC♯, v3D |
| 55 | 1157.89 | ^C𝄪, ^D♭ | vC♯, vvD |
| 56 | 1178.95 | vC♯𝄪, vD | C♯, vD |
| 57 | 1200.00 | D | D |
Notation
Ups and downs notation
Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
||||||
| Flat symbol | |
|
Using Helmholtz–Ellis accidentals, 57edo can also be notated using alternative ups and downs:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
Here, a sharp raises by three steps, and a flat lowers by three steps, so arrows can be used to fill in the gap. If the arrows are taken to have their own layer of enharmonic spellings, some notes may be best spelled with double arrows.
Sagittal notation
This notation uses the same sagittal sequence as EDOs 50, 64, and 71b, and is a superset of the notation for 19-EDO.
Evo flavor

Revo flavor

In the diagrams above, a sagittal symbol followed by an equals sign (=) means that the following comma is the symbol's primary comma (the comma it exactly represents in JI), while an approximately equals sign (≈) means it is a secondary comma (a comma it approximately represents in JI). In both cases the symbol exactly represents the tempered version of the comma in this EDO.
Scales
- 2 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 1 - 3mos of type 18L 21s (augene)
Instruments
Since 57edo contains 19edo as a non-trivial subset, it would be possible to use three 19edo instruments tuned 1\57 apart from each other to play the full gamut of 57edo.
A Lumatone mapping for 57edo is available.
Music
- 57edo improv (2025)