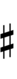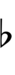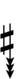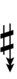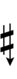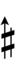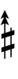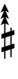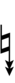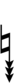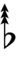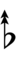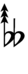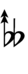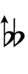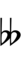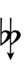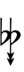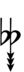91edo
| ← 90edo | 91edo | 92edo → |
91 equal divisions of the octave (abbreviated 91edo or 91ed2), also called 91-tone equal temperament (91tet) or 91 equal temperament (91et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 91 equal parts of about 13.2 ¢ each. Each step represents a frequency ratio of 21/91, or the 91st root of 2.
Theory
The harmonics 3, 5 and 7 for 91edo are on the flat side, making this a mostly flat system. It tempers out 15625/15552 in the 5-limit, 225/224 and 4375/4374 in the 7-limit, 245/242, 385/384 in the 11-limit, and 105/104, 144/143, 196/195 in the 13-limit. It provides the optimal patent val for 11- and 13-limit septimin temperament, and the 13-limit rank-3 tripod temperament, as well as the 11-limit rank-4 temperament tempering out 245/242 and the 13-limit rank-5 temperament tempering out 105/104, or rank-4 tempering out 105/104 and 144/143, or else 105/104 and 196/195 and hence 225/224 also.
Using the 91c val, it is audibly indistinguishable from a closed system of 1/7-comma meantone, with a 5th only 0.018 cents sharper. The chromatic semitone in this scale corresponds to 135/128, the eigenmonzo (unchanged-interval) of 1/7-comma meantone. Being 7 steps, what is also remarkable is that in this instance the chromatic semitone is equal to one step of 13edo. Since 135/128 is also equal to 1/13 of the octave, the 91c val tempers out the aluminium comma in the 5-limit.
The equal temperament also tempers out the [-11 26 -13⟩, the tridecatonic comma, which assigns 10/9 to 2/13 of the octave, and it supports trideci in the 7-limit, tempering out 4375/4374 and 83349/81920. It supports a variant of semaphore temperament which tempers out the [-42 23 2⟩ comma in the 2.3.7 subgroup, and is generated by a 19\91 generator. It is the second highest in a series of four consecutive edos that temper out quartisma ([24 -6 0 1 -5⟩), and as a corollary it is a tuning for the quartkeenlig temperament, which can also act as a stretched 23edo. In the 13-limit, it supports vidar and gives a reasonable tuning for its size.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -3.05 | -3.90 | -6.19 | -6.11 | +2.53 | +3.43 | +6.24 | +0.54 | +5.78 | +3.94 | +4.69 |
| Relative (%) | -23.2 | -29.5 | -46.9 | -46.3 | +19.2 | +26.0 | +47.3 | +4.1 | +43.9 | +29.9 | +35.6 | |
| Steps (reduced) |
144 (53) |
211 (29) |
255 (73) |
288 (15) |
315 (42) |
337 (64) |
356 (83) |
372 (8) |
387 (23) |
400 (36) |
412 (48) | |
Subsets and supersets
91 is the smallest composite number whose composite character is not immediately evident in the decimal system; it is, in fact, the product of 7 and 13. As such, 91edo contains 7edo and 13edo as subsets.
Miscellany
The concoctic scale for 91edo is 27 steps, where two concoctic neutral thirds make a sharp fifth of 54\91, representing 3/2 in the 91b val.
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-144 91⟩ | [⟨91 144]] | +0.963 | 0.964 | 7.31 |
| 2.3.5 | 15625/15552, 43046721/41943040 | [⟨91 144 211]] | +1.202 | 0.857 | 6.49 |
| 2.3.5.7 | 225/224, 4375/4374, 50421/50000 | [⟨91 144 211 255]] | +1.453 | 0.860 | 6.51 |
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 1 | 2\91 | 26.37 | 49/48 | Sfourth |
| 1 | 4\91 | 52.75 | 33/32 | Quartkeenlig (91f) |
| 1 | 11\91 | 145.05 | 49/45 | Swetneus (91ef) |
| 1 | 19\91 | 250.55 | 1240029/1048576 | Semaphore variant (24 & 91)** |
| 1 | 20\91 | 263.74 | 7/6 | Septimin (91) |
| 1 | 24\91 | 316.48 | 6/5 | Catakleismic (91f) |
| 1 | 33\91 | 435.16 | 9/7 | Supermajor |
| 1 | 34\91 | 448.35 | 35/27 | Semidimfourth |
| 1 | 38\91 | 501.10 | 4/3 | Python |
| 1 | 44\91 | 580.22 | 7/5 | Tritonic |
| 7 | 38\91 (1\91) |
501.10 (13.19) |
4/3 (81/80) |
Absurdity |
| 13 | 38\91 (1\91) |
501.10 (13.19) |
4/3 (265/252) |
Trideci (91) Aluminium (91c) |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
** Derived from scales in the Scales section, official name not decided upon yet.
Interval table
| Steps | Cents | Approximate ratios | Ups and downs notation |
|---|---|---|---|
| 0 | 0 | 1/1 | D |
| 1 | 13.2 | ^D, E♭♭ | |
| 2 | 26.4 | ^^D, ^E♭♭ | |
| 3 | 39.6 | ^3D, ^^E♭♭ | |
| 4 | 52.7 | 32/31, 33/32, 34/33 | v3D♯, ^3E♭♭ |
| 5 | 65.9 | vvD♯, v3E♭ | |
| 6 | 79.1 | 23/22 | vD♯, vvE♭ |
| 7 | 92.3 | 39/37 | D♯, vE♭ |
| 8 | 105.5 | 17/16, 33/31 | ^D♯, E♭ |
| 9 | 118.7 | 15/14 | ^^D♯, ^E♭ |
| 10 | 131.9 | 27/25, 41/38 | ^3D♯, ^^E♭ |
| 11 | 145.1 | 37/34 | v3D𝄪, ^3E♭ |
| 12 | 158.2 | 34/31 | vvD𝄪, v3E |
| 13 | 171.4 | 32/29 | vD𝄪, vvE |
| 14 | 184.6 | 10/9 | D𝄪, vE |
| 15 | 197.8 | 28/25, 37/33 | E |
| 16 | 211 | 26/23 | ^E, F♭ |
| 17 | 224.2 | 33/29 | ^^E, ^F♭ |
| 18 | 237.4 | 39/34 | ^3E, ^^F♭ |
| 19 | 250.5 | 37/32 | v3E♯, ^3F♭ |
| 20 | 263.7 | vvE♯, v3F | |
| 21 | 276.9 | 34/29 | vE♯, vvF |
| 22 | 290.1 | 13/11 | E♯, vF |
| 23 | 303.3 | 25/21, 31/26 | F |
| 24 | 316.5 | 6/5 | ^F, G♭♭ |
| 25 | 329.7 | 23/19, 29/24 | ^^F, ^G♭♭ |
| 26 | 342.9 | 39/32 | ^3F, ^^G♭♭ |
| 27 | 356 | v3F♯, ^3G♭♭ | |
| 28 | 369.2 | vvF♯, v3G♭ | |
| 29 | 382.4 | vF♯, vvG♭ | |
| 30 | 395.6 | 39/31 | F♯, vG♭ |
| 31 | 408.8 | ^F♯, G♭ | |
| 32 | 422 | 37/29 | ^^F♯, ^G♭ |
| 33 | 435.2 | 9/7 | ^3F♯, ^^G♭ |
| 34 | 448.4 | 22/17, 35/27 | v3F𝄪, ^3G♭ |
| 35 | 461.5 | vvF𝄪, v3G | |
| 36 | 474.7 | vF𝄪, vvG | |
| 37 | 487.9 | F𝄪, vG | |
| 38 | 501.1 | G | |
| 39 | 514.3 | 31/23, 39/29 | ^G, A♭♭ |
| 40 | 527.5 | ^^G, ^A♭♭ | |
| 41 | 540.7 | 26/19 | ^3G, ^^A♭♭ |
| 42 | 553.8 | 11/8 | v3G♯, ^3A♭♭ |
| 43 | 567 | 25/18 | vvG♯, v3A♭ |
| 44 | 580.2 | 7/5 | vG♯, vvA♭ |
| 45 | 593.4 | 31/22 | G♯, vA♭ |
| 46 | 606.6 | ^G♯, A♭ | |
| 47 | 619.8 | 10/7 | ^^G♯, ^A♭ |
| 48 | 633 | 36/25 | ^3G♯, ^^A♭ |
| 49 | 646.2 | 16/11 | v3G𝄪, ^3A♭ |
| 50 | 659.3 | 19/13 | vvG𝄪, v3A |
| 51 | 672.5 | vG𝄪, vvA | |
| 52 | 685.7 | G𝄪, vA | |
| 53 | 698.9 | A | |
| 54 | 712.1 | ^A, B♭♭ | |
| 55 | 725.3 | ^^A, ^B♭♭ | |
| 56 | 738.5 | ^3A, ^^B♭♭ | |
| 57 | 751.6 | 17/11, 37/24 | v3A♯, ^3B♭♭ |
| 58 | 764.8 | 14/9 | vvA♯, v3B♭ |
| 59 | 778 | vA♯, vvB♭ | |
| 60 | 791.2 | 41/26 | A♯, vB♭ |
| 61 | 804.4 | ^A♯, B♭ | |
| 62 | 817.6 | ^^A♯, ^B♭ | |
| 63 | 830.8 | ^3A♯, ^^B♭ | |
| 64 | 844 | v3A𝄪, ^3B♭ | |
| 65 | 857.1 | vvA𝄪, v3B | |
| 66 | 870.3 | 38/23 | vA𝄪, vvB |
| 67 | 883.5 | 5/3 | A𝄪, vB |
| 68 | 896.7 | 42/25 | B |
| 69 | 909.9 | 22/13 | ^B, C♭ |
| 70 | 923.1 | 29/17 | ^^B, ^C♭ |
| 71 | 936.3 | ^3B, ^^C♭ | |
| 72 | 949.5 | v3B♯, ^3C♭ | |
| 73 | 962.6 | vvB♯, v3C | |
| 74 | 975.8 | vB♯, vvC | |
| 75 | 989 | 23/13, 39/22 | B♯, vC |
| 76 | 1002.2 | 25/14, 41/23 | C |
| 77 | 1015.4 | 9/5 | ^C, D♭♭ |
| 78 | 1028.6 | 29/16 | ^^C, ^D♭♭ |
| 79 | 1041.8 | 31/17 | ^3C, ^^D♭♭ |
| 80 | 1054.9 | v3C♯, ^3D♭♭ | |
| 81 | 1068.1 | vvC♯, v3D♭ | |
| 82 | 1081.3 | 28/15 | vC♯, vvD♭ |
| 83 | 1094.5 | 32/17 | C♯, vD♭ |
| 84 | 1107.7 | ^C♯, D♭ | |
| 85 | 1120.9 | ^^C♯, ^D♭ | |
| 86 | 1134.1 | ^3C♯, ^^D♭ | |
| 87 | 1147.3 | 31/16, 33/17 | v3C𝄪, ^3D♭ |
| 88 | 1160.4 | vvC𝄪, v3D | |
| 89 | 1173.6 | vC𝄪, vvD | |
| 90 | 1186.8 | C𝄪, vD | |
| 91 | 1200 | 2/1 | D |
Other notations
Eliora's notation
Eliora, who believes the diatonic way of naming intervals in 91edo is not useful due to the fact that other temperaments and techniques for 91edo are more prominent, proposes a way of naming that merges the factors 7 and 13—7 equidistant notes are named do, re, mi, and 13 are named by some other virtue. The proposition is to use Old Slavic letter names, since no one uses them for naming or in mathematics. The 7 + 13 naming convention can be called a duality notation. Intervals can be named through Latin ones for the 7-note scale, and Greek ones for the 13-note.
| # | Eliora's Naming System | Eliora's Notation | Associated Ratio | |
|---|---|---|---|---|
| 0 | unison perfect prime perfect prota |
A Az (А) |
1/1 | |
| 1 | major prime major prota |
A# Az# |
1728/1715 | |
| 2 | augmented prota | Az## | ||
| 3 | biaugmented prota | Az### | ||
| 4 | bidiminished deiteria | Buki♭♭♭ | 33/32 | |
| 5 | diminished deiteria | Buki♭♭ | ||
| 6 | minor deiteria | Buki♭ | ||
| 7 | neutral deiteria | Buki (Б) | 135/128 | |
| 8 | major deiteria | Buki# | ||
| 9 | augmented deiteria | Buki## | ||
| 10 | biaugmented deiteria | Buki### | ||
| 11 | bidiminished tritia | Vedi♭♭♭ | 13/12, 12/11 | |
| 12 | diminished tritia | Vedi♭♭ | ||
| 13 | neutral secunde minor tritia |
B Vedi♭ |
11/10 | |
| 14 | neural tritia | Vedi (В) | 10/9 | |
| 15 | major tritia | Vedi# | 9/8 | |
| 16 | augmented tritia | Vedi## | ||
| 17 | biaugmented tritia | Vedi### | ||
| 18 | bidiminished tesseria | Glagol♭♭♭ | 8/7 | |
| 19 | diminished tesseria | Glagol♭♭ | ||
| 20 | minor tesseria | Glagol♭ | 7/6 | |
| 21 | neutral tesseria | Glagol (Г) | ||
| 22 | major tesseria | Glagol# | 13/11 | |
| 23 | augmented tesseria | Glagol## | ||
| 24 | biaugmented tesseria | Glagol### | 6/5 | |
| 25 | bidiminished pemptia | Dobro♭♭♭ | ||
| 26 | neutral tertie diminished pemptia |
C Dobro♭♭ |
11/9 | |
| 27 | major tertie minor pemptia |
C# Dobro♭ |
16/13, 27/22 | |
| 28 | neutral pemptia | Dobro (Д) | ||
| 29 | major pemptia | Dobro# | 5/4 | |
| 30 | augmented pemptia | Dobro## | ||
| 31 | biaugmented pemptia | Dobro### | ||
| 32 | bidiminished hektia | Yest♭♭♭ | 14/11 | |
| 33 | diminished hektia | Yest♭♭ | 9/7 | |
| 34 | minor hektia | Yest♭ | ||
| 35 | neutral hektia | Yest (Е) | ||
| 36 | major hektia | Yest# | ||
| 37 | augmented hektia | Yest## | ||
| 38 | biaugmented hektia | Yest### | 4/3 | |
| 39 | neutral quarte bidiminished hebdomia |
D Zhivete♭♭♭ |
||
| 40 | diminished hebdomia | Zhivete♭♭ | ||
| 41 | minor hebdomia | Zhivete♭ | ||
| 42 | neutral hebdomia | Zhivete (Ж) | 11/8 | |
| 43 | major hebdomia | Zhivete# | ||
| 44 | augmented hebdomia | Zhivete## | 7/5 | |
| 45 | biaugmented hebdomia | Zhivete### | ||
| 46 | bidiminished ogdonia | Dzelo♭♭♭ | ||
| 47 | diminished ogdonia | Dzelo♭♭ | 10/7 | |
| 48 | minor ogdonia | Dzelo♭ | ||
| 49 | neutral ogdonia | Dzelo (Ѕ) | ||
| 52 | neutral quinte | E | 121/81 | |
| 53 | major quinte | E# | 3/2 | |
| 54 | augmented quinte diminished ennatia |
E## Zemle♭♭ |
256/169 | |
| 55 | minor ennatia | Zemle♭ | ||
| 56 | neutral ennatia | Zemle (З) | ||
| 63 | neutral decatia | Izhe (И) | ||
| 64 | major decatia minor sexte |
Izhe# F♭ |
||
| 65 | neutral sexte | F | ||
| 70 | neutral hendecatia | Jerve (Ђ) | ||
| 77 | neutral dodecatia | Kako (К) | ||
| 78 | neutral septime | G | ||
| 84 | neutral decatotritia | Ludi (Л) | ||
| 91 | perfect octave perfect decatotetartia |
A Az (А) |
2/1 exact |
Scales
- Semaphore5: 19 15 19 19 19
- Semaphore9: 15 4 15 4 15 4 15 15 4
- Semaphore14: 4 11 4 4 11 4 4 11 4 11 4 4 11 4
- NaiveMajor[7]: 13 16 10 13 16 13 10
- NaiveMinor[7]: 13 10 16 13 10 13 16
- Septimin[9]: 11 9 11 9 11 9 11 9 11
- SeptiminHijaz[9]: 5 15 11 9 11 9 5 15 11
- Meantone[12]: 878787887878
- Meantone43 in 91edo
- Meantone55 in 91edo
- NaiveOrwell[13]: 5795797597579
- ArabicNaiveOrwell[13]: 1 11 9 5 1 15 7 5 9 7 1 11 9
- HungarianNaiveSurorwell[13]: 7 7 8 6 11 5 5 7 10 4 4 13 4
- Quartkeenlig[23]: 44444444444444444444443
- ConcocticSubset[7]: 17 10 17 10 17 10 17
- ConcocticMaqamSikah: 10 17 17 10 10 17 10