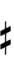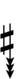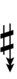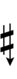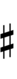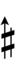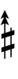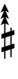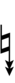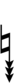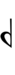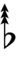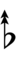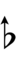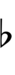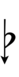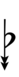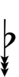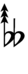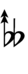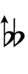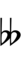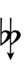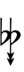82edo
| ← 81edo | 82edo | 83edo → |
82 equal divisions of the octave (abbreviated 82edo or 82ed2), also called 82-tone equal temperament (82tet) or 82 equal temperament (82et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 82 equal parts of about 14.6 ¢ each. Each step represents a frequency ratio of 21/82, or the 82nd root of 2.
Theory
82edo's patent val is contorted in the 11-limit, since 82 = 2 × 41. In the 13-limit the patent val tempers out 169/168 and 676/675, and in the 17-limit tempers out 273/272. It provides the optimal patent val for soothsaying temperament and supports baladic temperament. The 82d val tempers out 50/49 and is an excellent tuning for astrology and byhearted, surpassing their optimal patent vals. The alternative 82e val tempers out 121/120 instead.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | +0.48 | -5.83 | -2.97 | +4.78 | -6.38 | -2.52 | -4.83 | +0.99 | -5.19 | -3.57 |
| Relative (%) | +0.0 | +3.3 | -39.8 | -20.3 | +32.7 | -43.6 | -17.2 | -33.0 | +6.8 | -35.4 | -24.4 | |
| Steps (reduced) |
82 (0) |
130 (48) |
190 (26) |
230 (66) |
284 (38) |
303 (57) |
335 (7) |
348 (20) |
371 (43) |
398 (70) |
406 (78) | |
Subsets and supersets
82edo contains 2edo and 41edo as subsets. 164edo, which doubles it, is a notable tuning.
A step of 82edo is exactly 30 minas.
Intervals
| # | Cents | Approximate ratios* | Additional ratios | |
|---|---|---|---|---|
| Using the 82e val | Using the patent val | |||
| 0 | 0.000 | 1/1 | 1/1 | 1/1 |
| 1 | 14.634 | 65/64, 91/90 | 55/54 | |
| 2 | 29.268 | 49/48, 50/49, 81/80, 126/125 | 45/44, 55/54 | |
| 3 | 43.902 | 40/39 | 33/32, 45/44 | |
| 4 | 58.537 | 25/24, 28/27, 36/35 | 33/32 | |
| 5 | 73.171 | 26/25, 27/26 | 22/21 | |
| 6 | 87.805 | 19/18, 20/19, 21/20 | 22/21 | |
| 7 | 102.439 | 17/16, 18/17 | ||
| 8 | 117.073 | 15/14, 16/15 | ||
| 9 | 131.707 | 14/13, 13/12 | ||
| 10 | 146.341 | 12/11 | ||
| 11 | 160.976 | 11/10, 12/11 | ||
| 12 | 175.610 | 10/9, 21/19 | 11/10 | |
| 13 | 190.244 | 19/17 | ||
| 14 | 204.878 | 9/8 | ||
| 15 | 219.512 | 17/15 | ||
| 16 | 234.146 | 8/7 | ||
| 17 | 248.780 | 15/13 | 22/19 | |
| 18 | 263.415 | 7/6 | 22/19 | |
| 19 | 278.049 | 20/17 | 13/11 | |
| 20 | 292.683 | 19/16 | 13/11 | |
| 21 | 307.317 | |||
| 22 | 321.951 | 6/5 | ||
| 23 | 336.585 | 17/14 | 11/9 | |
| 24 | 351.220 | 11/9 | ||
| 25 | 365.854 | 16/13, 21/17, 26/21 | ||
| 26 | 380.488 | 5/4 | ||
| 27 | 395.122 | |||
| 28 | 409.756 | 19/15, 24/19 | 14/11 | |
| 29 | 424.390 | 14/11 | ||
| 30 | 439.024 | 9/7 | 22/17 | |
| 31 | 453.659 | 13/10 | 22/17 | |
| 32 | 468.293 | 17/13, 21/16 | ||
| 33 | 482.927 | |||
| 34 | 497.561 | 4/3 | ||
| 35 | 512.195 | |||
| 36 | 526.829 | 19/14 | 15/11 | |
| 37 | 541.463 | 26/19 | 11/8, 15/11 | |
| 38 | 556.098 | 11/8 | ||
| 39 | 570.732 | 18/13 | ||
| 40 | 585.366 | 7/5 | ||
| 41 | 600.000 | 17/12, 24/17 | ||
| … | … | |||
* As a no-11 19-limit temperament
Notation
Ups and downs notation
60edo can be notated using ups and downs notation using Helmholtz–Ellis accidentals:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|||||||||||||||||||
| Flat symbol |
Approximation to JI
Zeta peak index
| Tuning | Strength | Octave (cents) | Integer limit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per 8ve |
Step size (cents) |
Height | Integral | Gap | Size | Stretch | Consistent | Distinct | |
| Tempered | Pure | |||||||||
| 448zpi | 81.954146 | 14.642334 | 6.653983 | 5.154524 | 0.941321 | 14.718732 | 1200.671416 | 0.671416 | 8 | 8 |