143edo
| ← 142edo | 143edo | 144edo → |
143 equal divisions of the octave (abbreviated 143edo or 143ed2), also called 143-tone equal temperament (143tet) or 143 equal temperament (143et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 143 equal parts of about 8.39 ¢ each. Each step represents a frequency ratio of 21/143, or the 143rd root of 2.
143edo is only consistent to the 5-odd-limit, and the error of the harmonic 3 is quite large.
The 143b val provides a tuning almost identical with that of the POTE tuning for 7-limit meantone.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +2.94 | -0.30 | -3.79 | -2.51 | +2.53 | -1.37 | +2.64 | +4.14 | -3.81 | -0.85 | +1.10 |
| Relative (%) | +35.0 | -3.6 | -45.2 | -29.9 | +30.1 | -16.3 | +31.5 | +49.3 | -45.4 | -10.1 | +13.1 | |
| Steps (reduced) |
227 (84) |
332 (46) |
401 (115) |
453 (24) |
495 (66) |
529 (100) |
559 (130) |
585 (13) |
607 (35) |
628 (56) |
647 (75) | |
Subsets and supersets
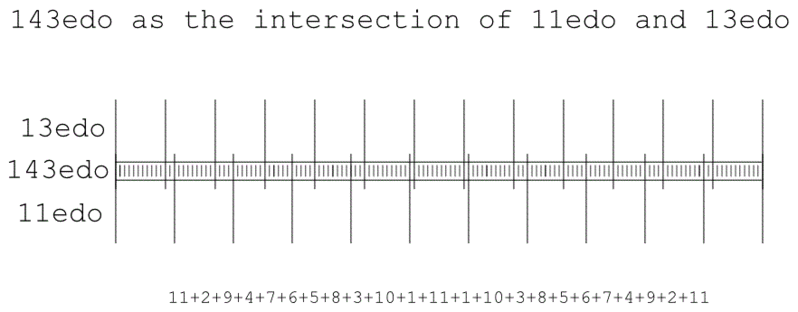
As 143 is 11 × 13, 143edo allows the polymicrotonal juxtaposition of 11edo and 13edo:
If the 11edo and 13edo subsets are analyzed as two scales that share the tonic and are then combined (as in the diagram above), the resulting scale would have 23 tones in the octave; otherwise, it would have 24.