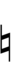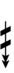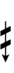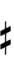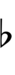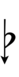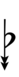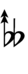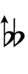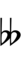120edo

From Xenharmonic Wiki
Jump to navigation Jump to search
← 119edo 120edo 121edo →
Prime factorization 23 × 3 × 5
Step size 10¢ 
Fifth 70\120 (700¢) (→7\12)
Semitones (A1:m2) 10:10 (100¢ : 100¢)
Consistency limit 3
Distinct consistency limit 3
Special properties

120 equal divisions of the octave (abbreviated 120edo or 120ed2), also called 120-tone equal temperament (120tet) or 120 equal temperament (120et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 120 equal parts of exactly 10 ¢ each. Each step represents a frequency ratio of 21/120, or the 120th root of 2.

Theory

120edo shares the perfect fifth with 12edo, tempering out the Pythagorean comma. 120edo is an excellent tuning in the 2.3.7.11.13.23.29 subgroup. In the no-5's 11-limit, it tempers out 243/242. In the patent val 120edo is also a tuning for the 7-limit decoid temperament.

The 120bdd val is a tuning for superpyth where 3/2 is tuned to exactly 710 cents. It may be used as a de facto dual fifth in newcome temperament.

Prime harmonics

Approximation of prime harmonics in 120edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0.00 -1.96 +3.69 +1.17 -1.32 -0.53 -4.96 +2.49 +1.73 +0.42 +4.96
Relative (%) +0.0 -19.6 +36.9 +11.7 -13.2 -5.3 -49.6 +24.9 +17.3 +4.2 +49.6
Steps
(reduced) 		120
(0) 		190
(70) 		279
(39) 		337
(97) 		415
(55) 		444
(84) 		490
(10) 		510
(30) 		543
(63) 		583
(103) 		595
(115)

Subsets and supersets

120edo is the 10th highly composite edo and the 5th factorial edo (120 = 5! = 1 × 2 × 3 × 4 × 5). It has many subsets: 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, and 60.

Miscellaneous properties

Being the simplest division of the octave by the Germanic long hundred, it has a unit step which is the fine relative cent of 1edo.

120edo also has a concoctic generator that resembles the leap day excess of earth, 29\120 corresponding to 5 hours and 48 minutes.

JI approximation

The following tables show how 15-odd-limit intervals are represented in 120edo. Prime harmonics are in bold; inconsistent intervals are in italics.

15-odd-limit intervals in 120edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/8, 16/13 0.528 5.3
15/14, 28/15 0.557 5.6
11/6, 12/11 0.637 6.4
13/11, 22/13 0.790 7.9
7/4, 8/7 1.174 11.7
11/8, 16/11 1.318 13.2
13/12, 24/13 1.427 14.3
13/7, 14/13 1.702 17.0
15/8, 16/15 1.731 17.3
3/2, 4/3 1.955 19.6
15/13, 26/15 2.259 22.6
9/5, 10/9 2.404 24.0
11/7, 14/11 2.492 24.9
7/5, 10/7 2.512 25.1
11/9, 18/11 2.592 25.9
15/11, 22/15 3.049 30.5
7/6, 12/7 3.129 31.3
13/9, 18/13 3.382 33.8
5/4, 8/5 3.686 36.9
9/8, 16/9 3.910 39.1
13/10, 20/13 4.214 42.1
5/3, 6/5 4.359 43.6
9/7, 14/9 4.916 49.2
11/10, 20/11 4.996 50.0
15-odd-limit intervals in 120edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
13/8, 16/13 0.528 5.3
15/14, 28/15 0.557 5.6
11/6, 12/11 0.637 6.4
13/11, 22/13 0.790 7.9
7/4, 8/7 1.174 11.7
11/8, 16/11 1.318 13.2
13/12, 24/13 1.427 14.3
13/7, 14/13 1.702 17.0
15/8, 16/15 1.731 17.3
3/2, 4/3 1.955 19.6
15/13, 26/15 2.259 22.6
11/7, 14/11 2.492 24.9
7/5, 10/7 2.512 25.1
11/9, 18/11 2.592 25.9
15/11, 22/15 3.049 30.5
7/6, 12/7 3.129 31.3
13/9, 18/13 3.382 33.8
5/4, 8/5 3.686 36.9
9/8, 16/9 3.910 39.1
13/10, 20/13 4.214 42.1
11/10, 20/11 5.004 50.0
9/7, 14/9 5.084 50.8
5/3, 6/5 5.641 56.4
9/5, 10/9 7.596 76.0

Intervals

Steps Cents Approximate ratios Ups and downs notation
0 0 1/1 D
1 10 ^D, ^E♭♭
2 20 ^^D, ^^E♭♭
3 30 ^3D, ^3E♭♭
4 40 42/41, 43/42, 44/43, 45/44, 46/45 ^4D, ^4E♭♭
5 50 34/33 ^5D, v5E♭
6 60 29/28, 30/29 v4D♯, v4E♭
7 70 v3D♯, v3E♭
8 80 22/21, 45/43 vvD♯, vvE♭
9 90 20/19, 39/37 vD♯, vE♭
10 100 18/17 D♯, E♭
11 110 16/15, 49/46 ^D♯, ^E♭
12 120 15/14 ^^D♯, ^^E♭
13 130 14/13, 41/38 ^3D♯, ^3E♭
14 140 13/12 ^4D♯, ^4E♭
15 150 12/11 ^5D♯, v5E
16 160 45/41 v4D𝄪, v4E
17 170 32/29, 43/39 v3D𝄪, v3E
18 180 vvD𝄪, vvE
19 190 29/26, 48/43 vD𝄪, vE
20 200 37/33, 46/41 E
21 210 35/31, 44/39 ^E, ^F♭
22 220 42/37 ^^E, ^^F♭
23 230 8/7 ^3E, ^3F♭
24 240 23/20 ^4E, ^4F♭
25 250 37/32 ^5E, v5F
26 260 43/37 v4E♯, v4F
27 270 v3E♯, v3F
28 280 47/40 vvE♯, vvF
29 290 13/11 vE♯, vF
30 300 44/37 F
31 310 49/41 ^F, ^G♭♭
32 320 ^^F, ^^G♭♭
33 330 23/19 ^3F, ^3G♭♭
34 340 28/23, 45/37 ^4F, ^4G♭♭
35 350 49/40 ^5F, v5G♭
36 360 16/13 v4F♯, v4G♭
37 370 26/21 v3F♯, v3G♭
38 380 vvF♯, vvG♭
39 390 vF♯, vG♭
40 400 29/23, 34/27 F♯, G♭
41 410 19/15 ^F♯, ^G♭
42 420 37/29 ^^F♯, ^^G♭
43 430 41/32 ^3F♯, ^3G♭
44 440 40/31, 49/38 ^4F♯, ^4G♭
45 450 48/37 ^5F♯, v5G
46 460 30/23, 43/33 v4F𝄪, v4G
47 470 21/16 v3F𝄪, v3G
48 480 29/22 vvF𝄪, vvG
49 490 vF𝄪, vG
50 500 4/3 G
51 510 43/32, 47/35 ^G, ^A♭♭
52 520 ^^G, ^^A♭♭
53 530 19/14 ^3G, ^3A♭♭
54 540 41/30 ^4G, ^4A♭♭
55 550 11/8 ^5G, v5A♭
56 560 29/21 v4G♯, v4A♭
57 570 32/23 v3G♯, v3A♭
58 580 vvG♯, vvA♭
59 590 45/32 vG♯, vA♭
60 600 41/29 G♯, A♭
61 610 37/26 ^G♯, ^A♭
62 620 ^^G♯, ^^A♭
63 630 23/16 ^3G♯, ^3A♭
64 640 42/29 ^4G♯, ^4A♭
65 650 16/11 ^5G♯, v5A
66 660 41/28 v4G𝄪, v4A
67 670 28/19 v3G𝄪, v3A
68 680 43/29 vvG𝄪, vvA
69 690 vG𝄪, vA
70 700 3/2 A
71 710 ^A, ^B♭♭
72 720 44/29, 47/31 ^^A, ^^B♭♭
73 730 32/21 ^3A, ^3B♭♭
74 740 23/15 ^4A, ^4B♭♭
75 750 37/24 ^5A, v5B♭
76 760 31/20, 45/29 v4A♯, v4B♭
77 770 v3A♯, v3B♭
78 780 vvA♯, vvB♭
79 790 30/19, 41/26 vA♯, vB♭
80 800 27/17, 46/29 A♯, B♭
81 810 ^A♯, ^B♭
82 820 45/28 ^^A♯, ^^B♭
83 830 21/13 ^3A♯, ^3B♭
84 840 13/8 ^4A♯, ^4B♭
85 850 49/30 ^5A♯, v5B
86 860 23/14 v4A𝄪, v4B
87 870 38/23, 43/26 v3A𝄪, v3B
88 880 vvA𝄪, vvB
89 890 vA𝄪, vB
90 900 37/22 B
91 910 22/13, 49/29 ^B, ^C♭
92 920 ^^B, ^^C♭
93 930 ^3B, ^3C♭
94 940 ^4B, ^4C♭
95 950 45/26 ^5B, v5C
96 960 40/23 v4B♯, v4C
97 970 7/4 v3B♯, v3C
98 980 37/21 vvB♯, vvC
99 990 39/22 vB♯, vC
100 1000 41/23 C
101 1010 43/24 ^C, ^D♭♭
102 1020 ^^C, ^^D♭♭
103 1030 29/16 ^3C, ^3D♭♭
104 1040 ^4C, ^4D♭♭
105 1050 11/6 ^5C, v5D♭
106 1060 24/13 v4C♯, v4D♭
107 1070 13/7 v3C♯, v3D♭
108 1080 28/15 vvC♯, vvD♭
109 1090 15/8 vC♯, vD♭
110 1100 17/9 C♯, D♭
111 1110 19/10 ^C♯, ^D♭
112 1120 21/11 ^^C♯, ^^D♭
113 1130 ^3C♯, ^3D♭
114 1140 29/15 ^4C♯, ^4D♭
115 1150 33/17 ^5C♯, v5D
116 1160 41/21, 43/22, 45/23 v4C𝄪, v4D
117 1170 v3C𝄪, v3D
118 1180 vvC𝄪, vvD
119 1190 vC𝄪, vD
120 1200 2/1 D
Retrieved from "https://en.xen.wiki/index.php?title=120edo&oldid=149070"