Harmonotonic tuning
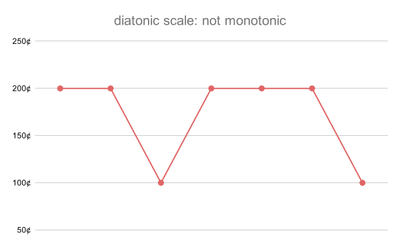
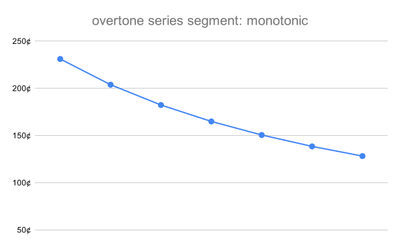
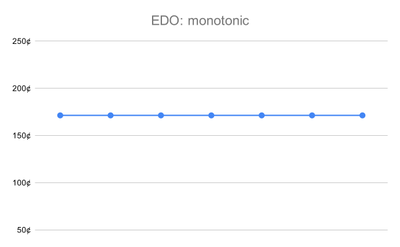
A harmonotonic tuning, or step-monotonic tuning, is one whose step sizes are monotonic: they do not both increase and decrease.
- A diatonic tuning is not harmonotonic because it goes back and forth between whole and half steps.
- A segment of the harmonic series is harmonotonic because its steps always decrease in size (within the interval of repetition).
- An EDO tuning is harmonotonic because the steps are all the same size.
Essentially, "harmonotonic" references the mathematical concept of monotonicity to form an umbrella term for tunings which are closely related to the harmonic series.
Categorization
Harmonotonic tunings can be categorized in two different ways: by shape, and by type.
Here are the three different shapes, according to their pitches sorted in ascending order:
- decreasing step size (e.g. harmonic series)
- equal step size (e.g. EDO)
- increasing step size (e.g. subharmonic series)
And here are the three different types:
- arithmetic & rational (e.g. harmonic or subharmonic series)
- arithmetic & irrational (e.g. EDO)
- non-arithmetic & irrational
Because different acronyms are used to distinguish rational (JI) tunings from general tunings which include irrational (non-JI) tunings, while the acronyms used for general tunings technically include the JI tunings, these general acronyms are more useful when reserved for non-JI tunings, and this is what is typically done. So when "irrational" is used on this page, it more accurately means "probably irrational".
Arithmetic tunings
See arithmetic tunings.
Non-arithmetic harmonotonic tunings
New arithmetic tunings can found by adding (or subtracting) a constant amount of frequency from the harmonic series. But addition is not the only operation we could try applying to the frequencies of a basic harmonotonic harmonic series.
The next operation above addition is multiplication. This operation is not very interesting, however, because multiplying frequency is equivalent to adding pitch, which does not meaningfully change a tuning; this merely transposes it. The reason multiplying frequency is equivalent to adding pitch is because pitch is found by taking the logarithm of frequency, and taking the logarithm of something effectively gears it down one operation lower on the hierarchy of operations: addition, multiplication, exponentiation, tetration, etc.
The next operation above multiplication is exponentiation. Exponentiating frequency is equivalent to multiplying pitch. Multiplying all pitch values does give you meaningfully new tunings. However, it does not preserve the arithmetic quality of a tuning for frequency or for pitch. So, these are now non-arithmetic tunings.
For example, we could start with the harmonic series, then take the square root of all the frequencies. This results in something like the harmonic series, except you don't reach the 2nd harmonic until the 4th step, the 3rd harmonic until the 9th step, or the 4th harmonic until the 16th step, etc. Because the square root is the same as raising to the power of 1/2, this is equivalent to multiplying all pitches by 1/2 (i.e. dividing them by 2). We could call this the 1/2-powharmonic series.
The next operation above exponentiation is tetration. Tetrating frequency is equivalent to exponentiating pitch. This operation and beyond will not be explored here.
Adding frequency is called shifting a tuning. Exponentiating frequency (or multiplying pitch) is called stretching (or compressing) a tuning.
Here is a table to illustrate:
| operation | frequency | pitch |
|---|---|---|
| shifting | addition | Gaussian logarithmic addition |
| transposition | multiplication | addition |
| stretching | exponentiation | multiplication |
| ... | tetration | exponentiation |
All powharmonic tunings are harmonotonic, but non-arithmetic and ir-rational.
Table of harmonotonic tunings
Shaahin Mohajeri has previously developed some tunings which qualify as harmonotonic. His n-ADO is equivalent to n-ODO, and his n-EDL is equivalent to a 2n-UDO (therefore EDL cannot be used to represent a UDO with an odd value for n).
Example harmonotonic tuning charts and graphs for comparison
Typically, the subharmonic series is displayed moving from 1/1, descending in pitch. To better illustrate the analogies between these different types of harmonotonic tunings, however, all tunings are shown starting on 1/1 but ascending in pitch. This means that all utonal tunings here were necessary to truncate, so that the lowest pitch would be known, so that the pitches' order could be reversed and the lowest pitch repositioned to 1/1 and all other pitches relative to that instead.
For a variety of perspectives, the frequency table values have been left unreduced, to illustrate the ideas behind the tuning better; the length values have been reduced.
The first several examples repeat after 4 steps. Their second repetition is italicized in the tables below.
In the charts, dots indicate places where values are rational with respect to the given quantity kind. Thicker lines indicate harmonotonic tunings which have equal steps in the given quantity kind.
| harmonotonic tuning | frequency (f) | pitch (log₂f) | length (1/f) | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | (0) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | (0) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 4-ODO = 4th harmonic mode = 4-ADO | (4/4) | 5/4 | 6/4 | 7/4 | 8/4 | 5/2 | 3/1 | 7/2 | 4/1 | (0) | 0.32 | 0.58 | 0.81 | 1.00 | 1.32 | 1.58 | 1.81 | 2.00 | (1/1) | 4/5 | 2/3 | 4/7 | 1/2 | 2/5 | 1/3 | 2/7 | 1/4 | |||
| 4-EDO = rank-1 temperament w/ generator 300¢ = APS⁴√2 ≈ APS1.189 | (2⁰⸍⁴) | 2¹⸍⁴ | 2²⸍⁴ | 2³⸍⁴ | 2⁴⸍⁴ | 2.38 | 2.83 | 3.36 | 4 | (0) | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | (1) | 0.84 | 0.71 | 0.59 | 0.50 | 0.42 | 0.35 | 0.30 | 0.25 | |||
| 4-UDO = 4th subharmonic mode | (8/8) | 8/7 | 8/6 | 8/5 | 8/4 | 16/7 | 8/3 | 16/5 | 4/1 | (0) | 0.19 | 0.42 | 0.68 | 1.00 | 1.19 | 1.42 | 1.68 | 2.00 | (1/1) | 7/8 | 3/4 | 5/8 | 1/2 | 7/16 | 3/8 | 5/16 | 1/4 | |||
| 4-EFDφ | (1+(0/4)(φ-1)) | 1+(1/4)(φ-1) | 1+(2/4)(φ-1) | 1+(3/4)(φ-1) | 1+(4/4)(φ-1) | 1.87 | 2.12 | 2.37 | 2.62 | (0) | 0.21 | 0.39 | 0.55 | 0.69 | 0.90 | 1.08 | 1.24 | 1.39 | (1) | 0.87 | 0.76 | 0.68 | 0.62 | 0.54 | 0.47 | 0.42 | 0.38 | |||
| 4-ELDφ | (1) | 1.11 | 1.24 | 1.40 | φ | 1.79 | 2.00 | 2.27 | 2.62 | (0) | 0.14 | 0.31 | 0.49 | 0.69 | 0.84 | 1.00 | 1.18 | 1.39 | (1) | 0.90 | 0.81 | 0.71 | 0.62 | 0.56 | 0.50 | 0.44 | 0.38 | |||
| harmonic series segment = 8-OS = 8-OD9 | (1/1) | 2/1 | 3/1 | 4/1 | 5/1 | 6/1 | 7/1 | 8/1 | 9/1 | (0) | 1.00 | 1.58 | 2.00 | 2.32 | 2.58 | 2.81 | 3.00 | 3.17 | (1/1) | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | |||
| subharmonic series segment = 8-US = 8-UD9 | (9/9) | 9/8 | 9/7 | 9/6 | 9/5 | 9/4 | 9/3 | 9/2 | 9/1 | (0) | 0.17 | 0.36 | 0.58 | 0.85 | 1.17 | 1.58 | 2.17 | 3.17 | (1/1) | 8/9 | 7/9 | 2/3 | 5/9 | 4/9 | 1/3 | 2/9 | 1/9 | |||
| 8-OS(3/4) | (4/4) | 7/4 | 10/4 | 13/4 | 16/4 | 19/4 | 22/4 | 25/4 | 28/4 | (0) | 0.81 | 1.32 | 1.70 | 2.00 | 2.25 | 2.46 | 2.64 | 2.81 | (1/1) | 4/7 | 2/5 | 4/13 | 1/4 | 4/19 | 2/11 | 4/25 | 1/7 | |||
| 8-US(3/4) | (28/28) | 28/25 | 28/22 | 28/19 | 28/16 | 28/13 | 28/10 | 28/7 | 28/4 | (0) | 0.16 | 0.35 | 0.56 | 0.81 | 1.11 | 1.49 | 2.00 | 2.81 | (1/1) | 25/28 | 11/14 | 19/28 | 4/7 | 13/28 | 5/14 | 1/4 | 1/7 | |||
| (1/⁴√2)-shifted harmonic series segment = 8-AFS(1/⁴√2) | (1) | 1.84 | 2.68 | 3.52 | 4.36 | 5.20 | 6.05 | 6.89 | 7.73 | (0) | 0.88 | 1.42 | 1.82 | 2.13 | 2.38 | 2.60 | 2.78 | 2.95 | (1) | 0.54 | 0.37 | 0.28 | 0.23 | 0.19 | 0.17 | 0.15 | 0.13 | |||
| (1/⁴√2)-shifted subharmonic series segment = 8-ALS(1/⁴√2) | (1) | 1.12 | 1.28 | 1.48 | 1.77 | 2.19 | 2.88 | 4.20 | 7.73 | (0) | 0.17 | 0.35 | 0.57 | 0.82 | 1.13 | 1.53 | 2.07 | 2.95 | (1) | 0.89 | 0.78 | 0.67 | 0.56 | 0.46 | 0.35 | 0.24 | 0.13 | |||
| AS5/4 = 1D JI lattice of 5/4 = 5/4 chain | (5⁰/4⁰) | 5¹/4¹ | 5²/4² | 5³/4³ | 5⁴/4⁴ | 5⁵/4⁵ | 5⁶/4⁶ | 5⁷/4⁷ | 5⁸/4⁸ | (0) | 0.32 | 0.64 | 0.97 | 1.29 | 1.61 | 1.93 | 2.25 | 2.58 | (1/1) | 4/5 | 16/25 | 64/125 | 256/625 | 1024/3125 | 4096/15625 | 16384/78125 | 65536/390625 | |||
| 8 pitches of 1/2-powharmonic series = harmonic series compressed by 1/2 | (√1) | √2 | √3 | √4 | √5 | √6 | √7 | √8 | √9 | (0) | 0.50 | 0.79 | 1.00 | 1.16 | 1.29 | 1.40 | 1.50 | 1.58 | (1) | 0.71 | 0.58 | 0.50 | 0.45 | 0.41 | 0.38 | 0.35 | 0.33 | |||
| 8 pitches of 1/2-subpowharmonic = subharmonic series compressed by 1/2 | (1) | 1.06 | 1.13 | 1.22 | 1.34 | 1.50 | 1.73 | 2.12 | 3 | (0) | 0.08 | 0.18 | 0.29 | 0.42 | 0.58 | 0.79 | 1.08 | 1.58 | (1) | 0.94 | 0.88 | 0.82 | 0.75 | 0.67 | 0.58 | 0.47 | 0.33 | |||
| 8 pitches of 2-logharmonic series | (1) | 1.58 | 2.00 | 2.32 | 2.58 | 2.81 | 3.00 | 3.17 | 3.32 | (0) | 0.66 | 1.00 | 1.22 | 1.37 | 1.49 | 1.58 | 1.66 | 1.73 | (1) | 0.63 | 0.50 | 0.43 | 0.39 | 0.36 | 0.33 | 0.32 | 0.30 | |||
| 8 pitches of 2-sublogharmonic series | (1) | 1.05 | 1.11 | 1.18 | 1.29 | 1.43 | 1.66 | 2.10 | 3.32 | (0) | 0.07 | 0.15 | 0.24 | 0.36 | 0.52 | 0.73 | 1.07 | 1.73 | (1) | 0.95 | 0.90 | 0.85 | 0.78 | 0.70 | 0.60 | 0.48 | 0.30 | |||
Notes on etymology
The "-tonic" root of "harmonotonic" does share etymology with the musical terms "tone" and "tonic". They both come from the Greek word "tonikos" which means "a stretching". This is also the explanation for "tonic" water, which supposedly relaxes you by stretching your muscles. So, the term "harmonotonic tuning" reunites these divergent applications of stretching — function values, and instrument strings — back into one place.
There is no relation between the "mono" Greek root meaning "one" and the "mon" in "harmony". It is just a fun coincidence that we can combine the two words this way.
Notes on monotonicity
Pitches of any tuning could be sorted in order to be monotonic, so for monotonicity to be meaningful for tunings, it must be applied to their steps after sorting their pitches.
Monotonicity is also used in another sense in xenharmonics, however, for scales, which are not order-agnostic. In these cases, the monotonicity does apply to the pitches, not the steps. See: https://en.xen.wiki/index.php?search=monotone&title=Special%3ASearch&go=Go
Monotonicity must also be restricted to within the interval of repetition to have much value. Otherwise, only scales with equal step sizes would qualify as monotonic, because any increase or decrease in step size would be countered with an opposite change once the scale repeated.
In mathematics, monotonicity is sometimes distinguished as strictly monotonic, when it is not permitted for a value to stay the same. In this sense, all tunings are strictly monotonic. But only some tunings are strictly step-monotonic. Of the tunings classified here, only those with increasing or decreasing step size are strictly step-monotonic.
The sequence of step-sizes is the "first difference" of the sequence of pitches. If you were to list the differences between the sizes of successive steps, that would be the second difference. A monotonic sequence, all of whose differences are monotonic, is called "absolutely monotonic". All tunings categorized here are absolutely monotonic.
History
Harmonotonic tunings are not at all new concepts. However, the classifications and manners of specification for harmonotonic and arithmetic tunings described here were developed by Douglas Blumeyer in March 2021, incorporating existing ideas and further significant input and guidance from Billy Stiltner, Shaahin Mohajeri, Paul Erlich, Joakim Bang Larsen, Dave Keenan, and Mike Battaglia. Discussion mostly occurred on Facebook on this comment thread. Other discussion occurred over email and private Facebook messages.
Dave and Mike independently suggested the term "step-monotonic" and prefer it to "harmonotonic" because it is more descriptive and mathematically accurate. Douglas does not disagree with those motivations or facts, but nonetheless prefers the name "harmonotonic" because it is friendly for non-mathematicians: it references the harmonic series, which is the core of this umbrella naming effort (with monotonicity merely happening-to-be-the-case, providing a convenient etymological root to reference).