Powharmonic series
Introduction
A powerharmonic series, like the harmonic series, is an infinitely ascending set of pitches from which scales can be drawn.
p-Powharmonic series
A powharmonic series can be built on any number [math]\displaystyle{ p }[/math], whether it is rational or irrational, positive or negative. The formula for a p-powharmonic series is simply:
[math]\displaystyle{ \qquad f(n) = n^p }[/math]
For example, the 0.69314718056-powharmonic series looks like this:
| Pitch | Frequency multiplier | Pitch | |||
|---|---|---|---|---|---|
| Definition | Decimal | Cents | Change (cents) | Octave-reduced (cents) | |
| 1 | 10.69314718056 | 1.0 | 0.0 | 0.0 | 0.0 |
| 2 | 20.69314718056 | 1.6 | 831.8 | 831.8 | 831.8 |
| 3 | 30.69314718056 | 2.1 | 1318.3 | 486.6 | 118.3 |
| 4 | 40.69314718056 | 2.6 | 1663.6 | 345.2 | 463.6 |
| 5 | 50.69314718056 | 3.1 | 1931.3 | 267.8 | 731.3 |
| 6 | 60.69314718056 | 3.5 | 2150.1 | 218.8 | 950.1 |
| 7 | 70.69314718056 | 3.9 | 2335.1 | 185.0 | 1135.1 |
| 8 | 80.69314718056 | 4.2 | 2495.3 | 160.2 | 95.3 |
| 9 | 90.69314718056 | 4.6 | 2636.7 | 141.3 | 236.7 |
| 10 | 100.69314718056 | 4.9 | 2763.1 | 126.4 | 363.1 |
| 11 | 110.69314718056 | 5.3 | 2877.5 | 114.4 | 477.5 |
| 12 | 120.69314718056 | 5.6 | 2981.9 | 104.4 | 581.9 |
The harmonic series is technically a powharmonic series, but it is the trivial case, with the exponent equal to 1. [math]\displaystyle{ p }[/math] closer to 1 give series closer to the harmonic series, in case a series is desired which is close enough to the harmonic series to evoke it but has some finely alternately tuned characteristics.
Multiplying the exponent of a powharmonic series by some constant c is equivalent to multiplying each of its pitches' cents by that constant c. For example, the 1.5-powharmonic series would be like stretching each octave of the harmonic series from 1200¢ to 1800¢. If you were to instead manipulate a harmonic series by adding or subtracting frequency, rather than exponentiating it, you instead get an AFS (arithmetic frequency sequence).
Using a negative power for the exponent gives a similar, but inverted effect. [math]\displaystyle{ f(n) = n^{-1} }[/math] is simply the subharmonic series. Other negative powers give you the subharmonic equivalent of their (super) powharmonic counterpart. You could call these subpowharmonic series.
log-base-b-of-a-Powharmonic series
Description
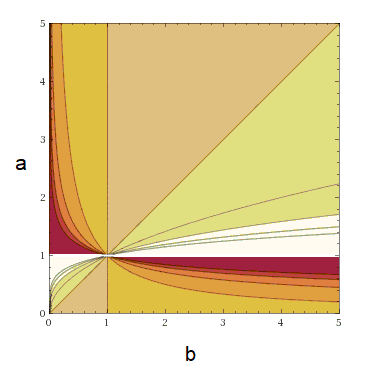
When we choose a [math]\displaystyle{ p }[/math] of the form [math]\displaystyle{ \log_{b}a }[/math], the resulting scale will include every integer power of [math]\displaystyle{ a }[/math], and the count of steps between each power of [math]\displaystyle{ a }[/math] will increase by a factor of [math]\displaystyle{ b }[/math].
Extending the naming scheme p-powharmonic series, we call this a log-base-b-of-a-powharmonic series.
Pitches per period
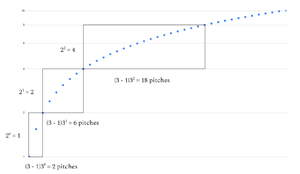
For example, the log-base-3-of-2-powharmonic series, where [math]\displaystyle{ p = log_{3}2 }[/math], will—like the harmonic series and by virtue of being "of 2"—include every octave (multiple of 2) of the fundamental. However, instead of the counts of pitches per octave increasing by a factor of 2:
[math]\displaystyle{ 2, 4, 8, 16… }[/math]
they will—by virtue of being "base-3"—increase by a factor of 3:
[math]\displaystyle{ 2, 6, 18, 54… }[/math]
Equality explanation
An equality involving exponents and logarithms helps us understand why:
[math]\displaystyle{ \qquad n^{\log_{b}a} = a^{log_{b}n} }[/math]
Breaking this down step by step:
- [math]\displaystyle{ \log_{b}n }[/math] gives the power to which [math]\displaystyle{ b }[/math] must be raised to give [math]\displaystyle{ n }[/math]
- whenever [math]\displaystyle{ n }[/math] is an integer power (squared, cubed, etc.) of [math]\displaystyle{ b }[/math], [math]\displaystyle{ \log_{b}n }[/math] will be an integer
- whenever [math]\displaystyle{ \log_{b}n }[/math] is an integer, we raise [math]\displaystyle{ a }[/math] to an integer power
- [math]\displaystyle{ n }[/math], being the pitch # or index, increments linearly by 1
- it takes longer and longer each time for [math]\displaystyle{ n }[/math] to reach the next power of [math]\displaystyle{ b }[/math]
Initial count
The first period of the series, determined by [math]\displaystyle{ a }[/math], will contain [math]\displaystyle{ b - 1 }[/math] pitches. For example, the log-base-4-of-5-powharmonic series' first 5/1 interval will contain [math]\displaystyle{ 4 - 1 = 3 }[/math] pitches.
Equivalences
The harmonic series features counts of pitches of increasing powers of 2 in each next octave, but it also contains counts of pitches of increasing powers of 3 in each next tritave, and counts of pitches in increasing powers of 5 in each next 5/1 interval, and so forth. This is because the harmonic series is equivalent to the log-base-2-of-2-powharmonic series, the log-base-3-of-3-powharmonic series, the log-base-5-of-5-powharmonic series, and so forth (the log-base-b-of-b-powharmonic series). This because any [math]\displaystyle{ \log_{b}b = 1 }[/math].
Any powharmonic series has infinite equivalent ways of being expressed. We can visualize the equivalences with the following coloration of powharmonic space:
a-Edharmonic series
Prerequisite: ln-of-a-powharmonic series
Irrational values can be used as [math]\displaystyle{ a }[/math] or [math]\displaystyle{ b }[/math].
In particular it may be of interest to use [math]\displaystyle{ e }[/math] as [math]\displaystyle{ b }[/math]—in other words, to use a natural logarithm.
For example, the ln-of-2-powharmonic series fits [math]\displaystyle{ e }[/math] times as many many more pitches into each next octave as the previous octave. Because [math]\displaystyle{ e }[/math] is irrational, however, no integer multiples of the octave will ever be reached.
In fact, this series is equivalent to the example given in the introduction, because [math]\displaystyle{ ln(2) ≈ 0.69314718056 }[/math], and if any powharmonic series were to qualify to be referred to for short as "the" powharmonic series, this would be the one.
Description
Perhaps even more interestingly, a ln-of-a-powharmonic series can be approximated by moving by steps of increasing equal divisions of [math]\displaystyle{ a }[/math].
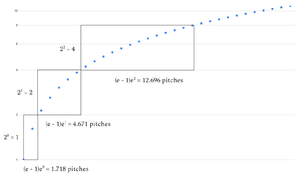
For example, if we first move by a step of 1ed2 (1200¢), then by 2ed2 (600¢), then 3ed2 (400¢), etc. we will soon find that the deltas between steps of our series are very close to the deltas between steps of the ln-of-2-powharmonic series. We could call this series the 2-edharmonic series.
Relation to ln-of-a-powharmonic series
The ratio between pitches of the ln-of-2-powharmonic series and the 2-edharmonic series approaches [math]\displaystyle{ 2^γ ≈ 1.49196704047 }[/math], where [math]\displaystyle{ γ }[/math] is the Euler-Mascheroni constant, [math]\displaystyle{ ≈ 0.5772156649 }[/math], which represents the difference between the natural logarithm and the mathematical harmonic series (as opposed to the musical harmonic series). This is because moving by steps of increasing equal divisions of [math]\displaystyle{ a }[/math] is equivalent to a series of pitches [math]\displaystyle{ 2^{H(n)} }[/math] where [math]\displaystyle{ H(n) }[/math] is the [math]\displaystyle{ n^{th} }[/math] harmonic number:
[math]\displaystyle{ \qquad H(1) = 1 \\ \qquad H(2) = \frac{3}{2} = 1 + \frac{1}{2} \\ \qquad H(3) = \frac{11}{6} = 1 + \frac{1}{2} + \frac{1}{3} \\ \qquad H(4) = \frac{25}{12} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} \\ \qquad … }[/math]
In other words, if we have gone by a step of 1ed2, we are at [math]\displaystyle{ 2^1 }[/math]. If we then go by a step of 2ed2, we have gone by [math]\displaystyle{ 2^1 · 2^{\frac12} = 2^{\frac32} }[/math]. And a further step of 3ed2 gets us to [math]\displaystyle{ 2^1 · 2^{\frac12} · 2^{\frac13} = 2^{\frac{11}{6}} }[/math], etc.
| Pitch # | ln-of-2-Powharmonic series | 2-Edharmonic series | Ratio between frequency multipliers | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency multiplier | Pitch | Frequency multiplier | Pitch | ||||||||
| Definition | Decimal | Cents | Change (cents) | Octave-reduced (cents) | Definition | Decimal | Cents | Change (cents) | Octave-reduced (cents) | ||
| 1 | 1ln(2) = 2ln(1) | 1 | 0.00 | — | 0.00 | 2H(1) = 21 | 2 | 1200.00 | — | 0.00 | 2 |
| 2 | 2ln(2) = 2ln(2) | 1.616806672 | 831.78 | 831.78 | 831.78 | 2H(2) = 23/2 | 2.828427125 | 1800.00 | 600.00 | 600.00 | 1.749391052 |
| 3 | 3ln(2) = 2ln(3) | 2.141486064 | 1318.33 | 486.56 | 118.33 | 2H(3) = 211/6 | 3.563594873 | 2200.00 | 400.00 | 1000.00 | 1.664075677 |
| 4 | 4ln(2) = 2ln(4) | 2.614063815 | 1663.55 | 345.22 | 463.55 | 2H(4) = 225/12 | 4.237852377 | 2500.00 | 300.00 | 100.00 | 1.621174033 |
| 5 | 5ln(2) = 2ln(5) | 3.05132936 | 1931.33 | 267.77 | 731.33 | 2H(5) = 2137/60 | 4.868014055 | 2740.00 | 240.00 | 340.00 | 1.595374829 |
| 6 | 6ln(2) = 2ln(6) | 3.462368957 | 2150.11 | 218.79 | 950.11 | 2H(6) = 249/20 | 5.464161027 | 2940.00 | 200.00 | 540.00 | 1.578156775 |
| 7 | 7ln(2) = 2ln(7) | 3.852807616 | 2335.09 | 184.98 | 1135.09 | 2H(7) = 2363/140 | 6.032922891 | 3111.43 | 171.43 | 711.43 | 1.56585106 |
| 8 | 8ln(2) = 2ln(8) | 4.226435818 | 2495.33 | 160.24 | 95.33 | 2H(8) = 2761/280 | 6.578949063 | 3261.43 | 150.00 | 861.43 | 1.556618708 |
| 9 | 9ln(2) = 2ln(9) | 4.585962562 | 2636.67 | 141.34 | 236.67 | 2H(9) = 27129/2520 | 7.105658007 | 3394.76 | 133.33 | 994.76 | 1.549436549 |
| 10 | 10ln(2) = 2ln(10) | 4.933409668 | 2763.10 | 126.43 | 363.10 | 2H(10) | 7.615655686 | 3514.76 | 120.00 | 1114.76 | 1.543690105 |
| 11 | 11ln(2) = 2ln(11) | 5.270337212 | 2877.47 | 114.37 | 477.47 | 2H(11) | 8.110986229 | 3623.85 | 109.09 | 23.85 | 1.538988096 |
| 12 | 12ln(2) = 2ln(12) | 5.597981231 | 2981.89 | 104.41 | 581.89 | 2H(12) | 8.593290568 | 3723.85 | 100.00 | 123.85 | 1.535069557 |
| 13 | 13ln(2) = 2ln(13) | 5.917342318 | 3077.94 | 96.05 | 677.94 | 2H(13) | 9.063911377 | 3816.16 | 92.31 | 216.16 | 1.531753765 |
| 14 | 14ln(2) = 2ln(14) | 6.22924506 | 3166.87 | 88.93 | 766.87 | 2H(14) | 9.523965051 | 3901.87 | 85.71 | 301.87 | 1.528911603 |
| 15 | 15ln(2) = 2ln(15) | 6.5343793 | 3249.66 | 82.79 | 849.66 | 2H(15) | 9.974392624 | 3981.87 | 80.00 | 381.87 | 1.526448369 |
| 16 | 16ln(2) = 2ln(16) | 6.833329631 | 3327.11 | 77.45 | 927.11 | 2H(16) | 10.41599671 | 4056.87 | 75.00 | 456.87 | 1.524293028 ... → 2γ = 1.49196704047 |
In yet other words, the definition of an a-edharmonic series is:
[math]\displaystyle{ \qquad f(n) = a^{H(n)} }[/math]
Naming details
We cross-pollinate the abbreviation for "equal division" with affiliation for the pronunciation of "enharmonic" to get the name "edharmonic series".
Due to the dominance of octave in music, we can actually refer to the 2-edharmonic series simply as the edharmonic series for short.
Other examples
As another example, the 3-edharmonic series would be moving first by a tritave (1ed3), then by 2ed3, 3ed3, 4ed3, etc.
Analogy with matharmonic series
Edharmonic series are to powharmonic series as the matharmonic series is to the logharmonic series.
Emulatory edharmonic series
The 0th harmonic number is not defined, however, if it were, it seems reasonable to assume it would be defined as 0; in other words, the first step of the harmonic series would be to add [math]\displaystyle{ \frac11 }[/math] to 0.
In accordance with this observation, it further seems reasonable that any a-edharmonic series could be prefixed with the frequency multiplier 1, rather than beginning straight away with the frequency multiplier [math]\displaystyle{ a }[/math].
In the case of the (2-)edharmonic series, doing so brings it closer in similarity to the (musical) harmonic series; the first step is exactly an octave, the second step a fifth (701.96¢ vs 600.00¢), the third step a fourth (498.04¢ vs 400.00¢), the fourth step a third, (386.31¢ vs 300¢), etc. This similarity could be useful when using the entire series as a scale rather than drawing scales from it. We therefore propose referring to this variation as the "emulatory edharmonic series", because it emulates the harmonic series.
| Pitch # | Harmonic series | Emulatory edharmonic series | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Frequency multiplier | Pitch | Frequency multiplier | Pitch | ||||||
| Decimal | Cents | Change (cents) | Octave-reduced (cents) | Definition | Decimal | Cents | Change (cents) | Octave-reduced (cents) | |
| 1 | 1.000000 | 0 | — | 0 | 2H(0) = 20 | 1.000000000 | 0 | — | 0 |
| 2 | 2.000000 | 1200 | 1200 | 0 | 2H(1) = 21 | 2.000000000 | 1200.00 | 1200.00 | 0.00 |
| 3 | 3.000000 | 1901.955001 | 701.955001 | 701.955001 | 2H(2) = 23/2 | 2.828427125 | 1800.00 | 600.00 | 600.00 |
| 4 | 4.000000 | 2400 | 498.044999 | 0 | 2H(3) = 211/6 | 3.563594873 | 2200.00 | 400.00 | 1000.00 |
| 5 | 5.000000 | 2786.313714 | 386.313714 | 386.313714 | 2H(4) = 225/12 | 4.237852377 | 2500.00 | 300.00 | 100.00 |
| 6 | 6.000000 | 3101.955001 | 315.6412870 | 701.955001 | 2H(5) = 2137/60 | 4.868014055 | 2740.00 | 240.00 | 340.00 |
| 7 | 7.000000 | 3368.825906 | 266.8709056 | 968.825906 | 2H(6) = 249/20 | 5.464161027 | 2940.00 | 200.00 | 540.00 |
| 8 | 8.000000 | 3600 | 231.1740935 | 0 | 2H(7) = 2363/140 | 6.032922891 | 3111.43 | 171.43 | 711.43 |
| 9 | 9.000000 | 3803.910002 | 203.9100017 | 203.910002 | 2H(8) = 2761/280 | 6.578949063 | 3261.43 | 150.00 | 861.43 |
| 10 | 10.000000 | 3986.313714 | 182.4037121 | 386.313714 | 2H(9) = 27129/2520 | 7.105658007 | 3394.76 | 133.33 | 994.76 |
| 11 | 11.000000 | 4151.317942 | 165.0042285 | 551.317942 | 2H(10) | 7.615655686 | 3514.76 | 120.00 | 1114.76 |
| 12 | 12.000000 | 4301.955001 | 150.6370585 | 701.955001 | 2H(11) | 8.110986229 | 3623.85 | 109.09 | 23.85 |
| 13 | 13.000000 | 4440.527662 | 138.5726609 | 840.527662 | 2H(12) | 8.593290568 | 3723.85 | 100.00 | 123.85 |
| 14 | 14.000000 | 4568.825906 | 128.2982447 | 968.825906 | 2H(13) | 9.063911377 | 3816.16 | 92.31 | 216.16 |
| 15 | 15.000000 | 4688.268715 | 119.4428083 | 1088.268715 | 2H(14) | 9.523965051 | 3901.87 | 85.71 | 301.87 |
| 16 | 16.000000 | 4800 | 111.7312853 | 0 | 2H(15) | 9.974392624 | 3981.87 | 80.00 | 381.87 |
An analogous emulatory matharmonic series exists.
See also
Harmonotonic tunings: powharmonic series are non-arithmetic harmonotonic tunings.
Logharmonic series: another type of non-arithmetic harmonotonic tuning.