Lattice
A lattice is a geometric construction that organizes pitches (or pitch classes) according to their intervallic relationships. In a lattice, pitches are represented by points, and tones that differ by a specific interval consistently appear in fixed relative positions to each other. These points can be connected by lines to highligh specific consonances. This creates a structure where pitch relationships can be analyzed through their geometric arrangement, which can be visualized in a lattice diagram.
Most lattice diagrams reduce the dimensionality by one through octave equivalence, meaning intervals separated by octaves are treated as equivalent points. This reduction makes a lattice diagram more comprehensible when projected onto a two-dimensional plane.
While lattices are often used to represent just intonation, they can also be applied to tempered spaces, in particular rank-3 systems generated by two distinct intervals (aside from the period) and which thus function equivalently to three-prime JI subgroups.
Tonnetz
The Tonnetz is a prominent example of a lattice representing 5-limit intervals. In its conventional hexagonal arrangement, the perfect fifth (3/2) and major third (5/4) intervals are positioned 60 degrees apart, with the major sixth (5/3) placed 60 degrees from the major third and 120 degrees from the perfect fifth. This arrangement results in 5-limit major triads (4:5:6) and minor triads (10:12:15) forming triangular patterns within the lattice structure.
The Tonnetz can be generalized to other subgroups with 3 primes, such as 2.3.7, where a respective fundamental chord such as 6:7:8 can be assigned to a triangle.
Higher dimensions
Lattices naturally extend into higher dimensions as more prime factors are incorporated into the tuning system. After applying octave reduction, a 5-limit system requires two dimensions, a 7-limit system requires three dimensions, and each additional prime factor adds another dimension to the full representation.
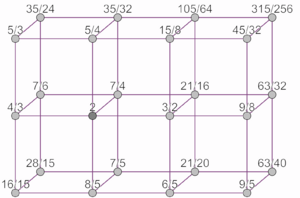
Vogel's Tonnetz extends Euler's 5-limit Tonnetz to the 7-limit, resulting in a three-dimensional diagram. This additional dimension allows for the representation of relationships involving the prime 7, adding intervals like the harmonic seventh (7/4) and the septimal minor third (7/6) alongside the 5-limit intervals.
Higher-dimensional lattices have been used by composers like Ben Johnston, and Kyle Gann to organize their harmonic materials. The lattice structure can guide everything from chord progressions to large-scale form, with paths through the lattice corresponding to harmonic progressions.
Isomorphic keyboards
- See also: Alternative keyboards
Isomorphic keyboards are a practical application of lattices in instrument design. An isomorphic keyboard is an instrument with a two-dimensional grid of buttons or keys, arranged so that any given sequence or combination of musical intervals maintains the same shape, regardless of where it occurs. This corresponds directly to a lattice: the keyboard layout is essentially a lattice mapped to physical space. This mapping creates consistent fingering patterns for musicians, where a particular chord shape or scale pattern can be transposed by simply moving the same finger configuration to a different position on the keyboard.
Unlike lattice diagrams that often reduce dimensionality through octave equivalence, isomorphic keyboards must physically represent all pitches. This effectively limits them to rank 2 systems, where the two-dimensional physical layout must accommodate the full range of playable notes. Quite often these are still tuned to EDOs, which are rank-1 systems. In such cases, there is an additional interval on the keyboard that is a unison, although it may be out of reach on the keyboard.
Examples of isomorphic keyboard designs include the Jankó keyboard, the Wicki–Hayden note layout and digital controllers like the Lumatone and Linnstrument. Isomorphic layouts are not limited to keyboards, skip fretting systems are also examples.

In mathematics
The lattices used in music theory correspond to mathematical structures of the same name.[note 1] In mathematical terms, a lattice is defined as a free abelian group embedded into Euclidean space. As expected, each point in the lattice represents a pitch class (or pitch), and the vectors between points represent musical intervals. The lattice is generated by a set of basis vectors corresponding to prime harmonics, or other fundamental intervals. The embedding into Euclidean space then also induces a norm onto intervals, which serves as a way of measuring complexity.
An example is the construction of Tenney-Euclidean interval space, which provides a metric for measuring harmonic distances between pitches. We map a p-limit JI space into R^n by representing each ratio as a vector, according to its prime decomposition. The axes are then scaled according to the logarithms of their respective primes, so prime 2 has length log2(2) = 1, prime 3 has length log2(3), and prime 5 has length log2(5), etc.
For the 5 limit, we get the embedding:
- [math]\displaystyle{ 2^x \cdot 3^y \cdot 5^z \to \left[x, y \log_2(3), z \log_2(5) \right] \in \mathbb{R}^3 }[/math]
When distances are measured in this space, we get the Tenney-Euclidean distance, a useful measure which is often used for finding optimal temperaments.
Gallery
-
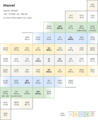
A square lattice representing marvel temperament.
-
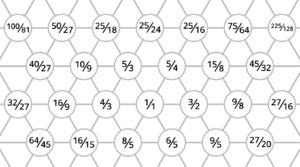
A hexagonal lattice representing 41edo's mapping of 5-limit intervals, using ups and downs notation.
-
A hexagonal lattice representing a subset of 7-limit intervals, using color notation.
-
A torus of notes in 15edo, notated by porcupine notation with LH-NiceIonian as the base scale.
See also
External links
- Beginner's guide to lattices: See chapter 1.3 of Alternative Tunings: Theory, Notation and Practice by Kite Giedraitis (2016)
- "lattice/lattice diagram" on Tonalsoft Encyclopedia
- "Octave Equivalent Music Lattices" by Graham Breed (2008)
- "Unison Vectors and Periodicity Blocks in the Three-Dimensional (3-5-7-) Harmonic Lattice of Notes" by Adriaan Fokker (1969)
- "Harmonic Lattice Diagrams" by Joseph L. Monzo (1998)