380edo
Jump to navigation
Jump to search
Prime factorization
22 × 5 × 19
Step size
3.15789¢
Fifth
222\380 (701.053¢) (→111\190)
Semitones (A1:m2)
34:30 (107.4¢ : 94.74¢)
Consistency limit
5
Distinct consistency limit
5
| ← 379edo | 380edo | 381edo → |
380 equal divisions of the octave (abbreviated 380edo or 380ed2), also called 380-tone equal temperament (380tet) or 380 equal temperament (380et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 380 equal parts of about 3.16 ¢ each. Each step represents a frequency ratio of 21/380, or the 380th root of 2.
Theory
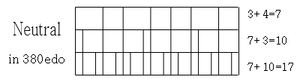
380edo notably provides the optimal patent val for the 2.3.11 subgroup neutral temperament. It has particularly accurate approximations of primes 23 and 29. Approximations of 7, 13, 17, and 19 are also very good.
Odd harmonics
| Harmonic | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.90 | -1.05 | +0.65 | +1.35 | +1.31 | -0.53 | +1.20 | -0.74 | -0.67 | -0.25 | +0.15 |
| Relative (%) | -28.6 | -33.3 | +20.5 | +42.8 | +41.6 | -16.7 | +38.2 | -23.6 | -21.2 | -8.1 | +4.6 | |
| Steps (reduced) |
602 (222) |
882 (122) |
1067 (307) |
1205 (65) |
1315 (175) |
1406 (266) |
1485 (345) |
1553 (33) |
1614 (94) |
1669 (149) |
1719 (199) | |
Subsets and supersets
Since 380 factors into 22 × 5 × 19, 380edo has subset edos 2, 4, 5, 10, 19, 20, 38, 76, 95, and 190.