No-twos subgroup temperaments
- This is a list showing technical temperament data. For an explanation of what information is shown here, you may look at the technical data guide for regular temperaments.
| Todo: WIP Further entries in the catalog of 3.5.7 subgroup rank two temperaments will eventually be documented here. |
This is a collection of subgroup temperaments which omit the prime harmonic of 2. Because of the absence of octaves, these are all nonoctave scales using a period of a tritave, or if harmonic 3 is also excluded, 5/1.
Overview by mapping of 5
Classified by focusing on the mapping of 5th harmonic, similar to Rank-2 temperaments by mapping of 3.
- Arcturus, Aldebaran and Polaris have a 3/1 period and ~5/3 generator. There is one-to-one correspondence between the 3.5 subgroup and mapped intervals.
- BPS has a ~9/7 generator, two of which give the ~5/3.
- Sirius has a ~25/21 generator, three of which give the ~5/3.
- Deneb has a ~11/9 generator, three of which give the ~9/5.
- Canopus has a ~7/5 generator, five of which give the ~27/5 (9/5 up a tritave).
- Alnilam has a ~81/55 generator, ten of which give the ~243/5 (9/5 up three tritaves).
- Izar has a ~16807/10125 generator, twelve of which give the ~2187/5 (9/5 up five tritaves).
- Nekkar has a ~16807/10935 generator, sixteen of which give the ~6561/5 (9/5 up six tritaves).
- Mintaka does not include the 5th harmonic, and has an ~11/7 generator, two of which give the ~27/11, and three of which give the ~27/7 (9/7 and a tritave).
- Antipyth uses 5/1 as a period, and has a ~7/5 generator. There is one-to-one correspondence between the 5.7 subgroup and mapped intervals.
- Juggernaut uses half-pentave(~11/5) as a period, and has a ~7/5 generator.
3.5.7 subgroup temperaments
Arcturus
As for extensions of this temperament that include the prime 2, see opossum, crepuscular, catalan, bunya, bohpier, and superkleismic.
Subgroup: 3.5.7
Comma list: 15625/15309
Sval mapping: [⟨1 0 -7], ⟨0 1 6]]
Sval mapping generators: ~3, ~5
POTE generator: ~5/3 = 878.042
Optimal ET sequence: b2, b11, b13
Badness (Sintel): 0.535
Polturus
This extension of Arcturus adds Polaris's mapping for 11/9, mapping it to 5 generators down.
Subgroup: 3.5.7.11
Comma list: 15625/15309, 177147/171875
Gencom: [3/1 5/3; 15625/15309 177147/171875]
Mapping: [⟨1 1 -1 5], ⟨0 1 6 -6]]
POTE generator: ~5/3 = 884.268
EDTs: 15, 13e, 28e, 43dee
Badness (Sintel): 2.507
BPS
For extensions to this temperament that include the octave, see Sensamagic clan. Non-octave extensions will be documented below.
Subgroup: 3.5.7
Comma list: 245/243
Sval mapping: [⟨1 1 2], ⟨0 2 -1]]
Sval mapping generators: ~3, ~9/7
Optimal tuning (POTE): ~3 = 1\1edt, ~9/7 = 440.4881
Optimal ET sequence: b4, b9, b13, b56, b69, b82, b95
Badness (Sintel): 0.066
Alhena
This is a strong extension to BPS in the subgroup 3.5.7.11/2.13/4 that equates the "semitone" of 27/25~49/45 to 13/12, and then three of these intervals to 14/11.
Subgroup: 3.5.7.11/2.13/4
Comma list: 196/195, 325/324, 1001/1000
Sval mapping: [⟨1 1 2 -1 2], ⟨0 2 -1 11 -4]]
Sval mapping generators: ~3, ~7/3
Optimal tuning (CWE): ~3 = 1\1edt, ~9/7 = 441.025
Supporting ETs: b13, b69, b56, b82, b43, b125, b30, b151, b95, b17é, b194d, b99, b181d, b108é (Note that é is used as the wart for 11/2.)
Badness (Sintel): 0.187
Mintra
This temperament splits 27/7 (the BPS generator up a tritave) into three by means of 11/7 or, equivalently, 7/1 in three by means of 21/11, and is the intersection of BPS, Deneb, and Mintaka temperaments as well as the most natural temperament satisfied in the 3.5.7.11 subgroup in 39edt.
Subgroup: 3.5.7.11
Comma list: 245/243, 1331/1323
Subgroup-val mapping: [⟨1 5 0 1], ⟨0 -6 3 2]]
Sval mapping generators: ~3, ~21/11
Optimal tuning (CWE): ~3 = 1\1edt, ~11/7 = 780.752
Supporting ETs: 39, 17, 56, 22, 5, 95, 12, 61, 73, 134, 27c, 151e, 100, 90
Badness (Sintel): 0.302
Tridecimal Mintra
This temperament uses the canonical extension for prime 13 described at Tridecimal Mintaka.
Subgroup: 3.5.7.11.13
Comma list: 245/243, 275/273, 1575/1573
Subgroup-val mapping: [⟨1 5 0 1 10], ⟨0 -6 3 2 -13]]
Sval mapping generators: ~3, ~21/11
Optimal tuning (CWE): ~3 = 1\1edt, ~11/7 = 780.428
Supporting ETs: 39, 17, 22, 56, 5f, 61, 95, 100, 134, 73f, 139cf, 83cf, 173e, 178cef
Badness (Sintel): 0.373
Dubhe
This temperament is a simple 3.5.7.17 weak extension of BPS that splits the generator of 9/7 into two intervals of 17/15. The name was suggested by MidnightBlue after Dubhe, a bright double star (the ninth brightest) and similarities to the word "double".
Subgroup: 3.5.7.17
Comma list: 245/243, 2025/2023
Subgroup-val mapping: [⟨1 1 2 2], ⟨0 4 -2 5]]
Optimal tuning (CWE): ~3 = 1\1edt, ~17/15 = 220.142
Supporting ETs: 26, 9, 17, 43, 69, 8, 35, 95, 61, 60, 121, 25g, 112, 44
Badness (Sintel): 0.177
Canopus
For extensions to this temperament that include the prime 2, see Mirkwai clan. No-twos extensions will be documented below.
Subgroup: 3.5.7
Comma list: 16875/16807
Subgroup-val mapping: [⟨1 3 3], ⟨0 -5 -4]]
Sval mapping generators: ~3, ~7/5
Optimal ET sequence: b13, b62, b75, b88, b101, b114, b355, b469, b583, b697
Badness (Sintel): 0.100
Suhail
Tempering out the 3.13-subgroup threedie splits the tritave into three, meeting 11/1 at seven generators after tempering out the sopreisma.
Subgroup: 3.5.7.11.13
Comma list: 1575/1573, 1625/1617, 4459/4455
Subgroup-val mapping: [⟨3 4 5 6 7], ⟨0 5 4 7 0]]
Sval mapping generators: ~13/9, ~65/63
Generator tunings:
WE TE Optimized 634.144, 49.695 634.1448, 49.6946 Constrained 1\b3 = 633.985, 49.733 1\b3 = 633.985, 49.839 Destretched 1\b3 = 633.985, 49.6825 1\b3 = 633.985, 49.6821
Optimal ET sequence: b39, b114, b153, b498cf, b651cf
Badness (Sintel): 0.330
Izar
Subgroup: 3.5.7
Comma list: 13841287201/13839609375
Subgroup-val mapping: [⟨1 7 5], ⟨0 -12 -7]]
Sval mapping generators: ~3, ~16807/10125
Optimal tuning (CTE): ~3 = 1\1edt, ~16807/10125 = 877.280
Optimal ET sequence: b13, b141, b154, ... b258, b271, b800, b1071, b1342, b1613, b4568, b6181
Badness (Sintel): 0.017
Nekkar
This temperament is the no-twos restriction of squares, and as such is named after a star that belonged to the obsolete constellation of Quadrans Muralis, whose name has to do with squares. However, seeing the sheer complexity and size of the commas, Nekkar is much more naturally thought of as 3.5.7.11 than 3.5.7, whereupon it becomes a strong extension of Mintaka.
Subgroup: 3.5.7
Comma list: 35303692060125/33232930569601
Subgroup-val mapping: [⟨1 8 3], ⟨0 -16 -3]]
Sval mapping generators: ~3, ~16807/10935
Optimal tuning (CWE): ~3 = 1\1edt, ~16807/10935 = 776.767
Supporting ETs: 22, 49, 5c, 71, 27, 17c, 120, 93, 76c, 32cc, 169d, 115, 191d, 164d
Badness (Sintel): 17.120
3.5.7.11 subgroup
See also Mintaka.
This continues the canonical 11-limit extension of squares.
Subgroup: 3.5.7.11
Comma list: 1331/1323, 120285/117649
Subgroup-val mapping: [⟨1 8 3 3], ⟨0 -16 -3 -2]]
Sval mapping generators: ~3, ~11/7
Optimal tuning (CWE): ~3 = 1\1edt, ~11/7 = 776.781
Supporting ETs: 22, 49, 71, 5c, 27, 120, 93, 17c, 76c, 169d, 191d, 115, 164d, 125cd
Badness (Sintel): 1.375
3.5.7.11.13 subgroup
This uses the Minalzidar mapping of 13.
Subgroup: 3.5.7.11.13
Comma list: 169/165, 351/343, 11011/10935
Subgroup-val mapping: [⟨1 8 3 3 6], ⟨0 -16 -3 -2 -9]]
Sval mapping generators: ~3, ~11/7
Optimal tuning (CWE): ~3 = 1\1edt, ~11/7 = 776.678
Supporting ETs: 22, 5c, 27, 49, 71f, 17cf
Badness (Sintel): 1.723
Procyon
This tempers out the Don Page comma between 7/5 and 9/7, allowing an accurate representation of the 5:7:9 chord, similar to the 3:5:7 in Sirius.
Subgroup: 3.5.7
Comma list: 823543/820125
Subgroup-val mapping: [⟨1 2 2], ⟨0 -7 -3]]
- sval mapping generators: ~3, ~17/9
Optimal tuning (CTE): ~3 = 1\1edt, ~49/45 = 145.333
Supporting ETs: b13, b157, b144, b170, b131, b183, b118, b14, b105, b12c, b196, b92, b27, b79
Badness (Sintel): 0.200
Erigone
Erigone splits the (tritave-augmented) generator of procyon into three, allowing for an accurate representation of 11/9 at -19 generators and 13/9 at -13 generators.
Comma list: 847/845, 1575/1573, 4459/4455
Subgroup-val mapping: [⟨1 9 5 9 7], ⟨0 -21 -9 -19 -13]]
Optimal tuning (WE): ~3 = 1901.9699, ~49/33 = 682.4486
Optimal tuning (CWE): ~3 = 1\1edt, ~49/33 = 682.4427
Optimal ET sequence: b25ce, b39, b92, b131, b170, b301, b471
Badness (Smith): 0.00271
Badness (Sintel): 0.21396
Hemigone
By tempering out 3971/3969, erigone's tritave-augmented generator (49/11) is split into two 19/9s. Then, 17/1 is approximated at 39/35 below 19/1 (tempering out 665/663).
Comma list: 665/663, 847/845, 1575/1573, 1617/1615, 4459/4455
Subgroup-val mapping: [⟨1 30 14 28 20 25 2], ⟨0 -42 -18 -38 -26 -33 1]]
Optimal tuning (WE): ~3 = 1902.0918, ~19/9 = 1292.3032
Optimal tuning (CWE): ~3 = 1\1edt, ~19/9 = 1292.2083
Optimal ET sequence: b25ce, b53, b78, b131, b209, b340
Badness (Smith): 0.00501
Badness (Sintel): 0.45479
(no-2s) 23-limit
2277/2275 may be used in the same way to extend the simpler erigone to the 3.5.7.11.13.23 subgroup.
Subgroup: 3.5.7.11.13.17.19.23
Comma list: 665/663, 847/845, 1575/1573, 1617/1615, 2277/2275, 4459/4455
Subgroup-val mapping: [⟨1 30 14 28 20 25 2 64], ⟨0 -42 -18 -38 -26 -33 1 -90]]
Optimal tuning (WE): ~3 = 1902.0149, ~19/9 = 1292.2401
Optimal tuning (CWE): ~3 = 1\1edt, ~19/9 = 1292.1988
Optimal ET sequence: b53i, b78i, b131, b340, b471
Badness (Smith): 0.00539
Badness (Sintel): 0.54174
Sirius
This tempers out the Don Page comma between 5/3 and 7/5, allowing an accurate representation of the 3:5:7 chord, similar to the 5:7:9 in Procyon.
For an overview of extensions to this temperament that include prime 2, see Gariboh clan#Overview to extensions.
Subgroup: 3.5.7
Comma list: 3125/3087
Subgroup-val mapping: [⟨1 1 1], ⟨0 3 5]]
- sval mapping generators: ~3, ~25/21
Optimal tuning (POTE): ~3 = 1\1edt, ~25/21 = 293.740
Optimal ET sequence: b6, b7, b13, b71, b84, b97, b110, b123, b136
Badness (Sintel): 0.213
Remus
By splitting the generator of Sirius into three, remus efficiently represents the no-2s 13-limit with MOS scales of 18, 25, 32, or 39 steps.
This is essentially electra but with prime 7, or more accurately, electra is the no-sevens restriction of this temperament.
Subgroup: 3.5.7.11.13
Comma list: 275/273, 1625/1617, 1575/1573
Subgroup-val mapping: [⟨1 4 6 5 6], ⟨0 -9 -15 -10 -13]]
- sval mapping generators: ~3, ~15/11
Optimal tuning (CWE): ~3 = 1\1edt, ~15/11 = 536.090
Supporting ETs: 39, 7, 32, 71, 110, 46, 149, 188, 181
Badness (Sintel): 0.286
Mizar
This temperament uses a weak extension to 3.5.7.17 similar to what Dubhe does: tempering out 2025/2023 to split the 7-limit generator in half; in this case, 25/7 is split into two intervals of 17/9, which turns out to occupy the position of a macrodiatonic fifth, specifically a macro-flattone fifth.
Subgroup: 3.5.7.17
Comma list: 3125/3087, 2025/2023
Subgroup-val mapping: [⟨1 -2 -4 2], ⟨0 6 10 1]]
- sval mapping generators: ~3, ~17/9
Optimal tuning (CWE): ~3 = 1\1edt, ~17/9 = 1097.800
Supporting ETs: 26, 7, 19, 45, 71, 97, 33, 123, 12d, 149, 59d, 175, 64d, 85cd
Badness (Sintel): 0.383
Full no-twos 17-limit
This exploits the Sirius tuning of the 25/21 generator being close to 13/11 (in order to split 7/5 evenly); additionally this tempers out 459/455, equating 17/13 to 35/27.
Subgroup: 3.5.7.11.13.17
Comma list: 275/273, 459/455, 1625/1617, 2025/2023
Subgroup-val mapping: [⟨1 -2 -4 12 11 2], ⟨0 6 10 -17 -15 1]]
- sval mapping generators: ~3, ~17/9
Optimal tuning (CWE): ~3 = 1\1edt, ~17/9 = 1098.298
Supporting ETs: 26, 71, 45, 19, 97f, 116d
Badness (Sintel): 0.841
Tuning diagrams
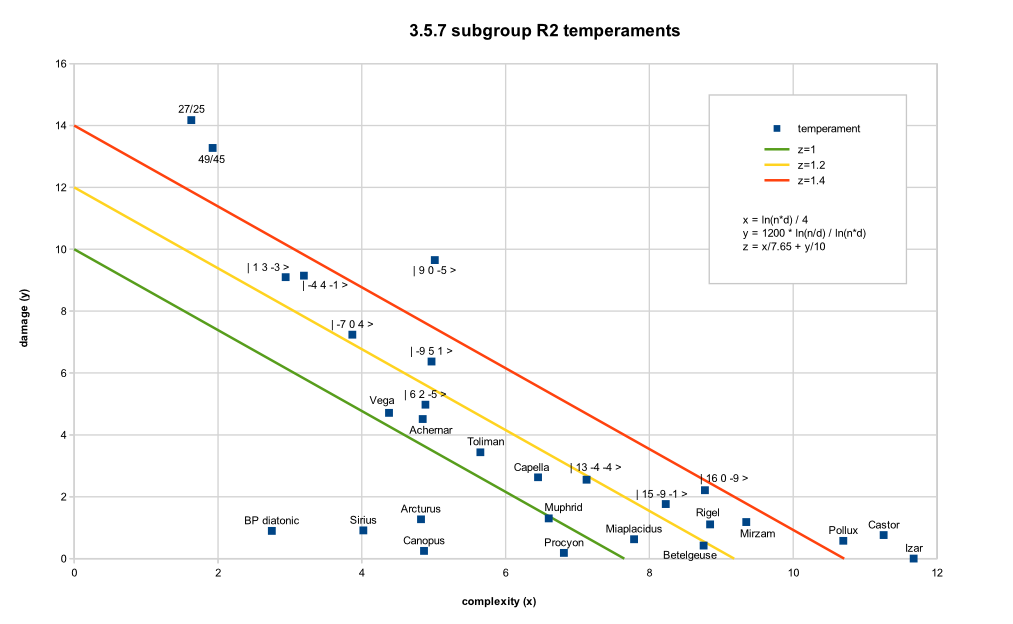
|
| Complexity vs. damage plot. z < 1 corresponds to the "Middle Path" inclusion criterion. |
3.5.11 subgroup temperaments
Polaris
Polaris tempers out the comma 177147/171875, and thus equates 7 5/3's with 15/11, or equivalently 7 9/5's with 11/9.
Subgroup: 3.5.11
Comma list: 177147/171875
Gencom: [3/1 5/3; 177147/171875]
Sval mapping: [⟨1 2 1], ⟨0 1 -6]]
POTE generator: ~5/3 = 892.6
EDTs: 17, 15, 32, 49, 13[+11], 47, 19, 11[+11], 81, 66, 79[+11], 62[+11], 28[+11], 21[-11]
Deneb
Subgroup: 3.5.11
Comma list: 6655/6561
Gencom: [3/1 11/9; 6655/6561]
Sval mapping: [⟨1 2 2], ⟨0 -3 1]]
POTE generator: ~11/9 = 340.242
EDTs: 28, 11, 17, 6, 39, 5, 67, 45, 50, 16, 23, 73, 61, 62
Fomalhaut
Fomalhaut is an extension of Deneb to higher limits that splits the interval of 11/3 in three.
The 23-limit version of Fomalhaut was created first, as an attempt to approximate the no-2s, no-7s 23-limit as accurately as possible using 25 to 35 notes per equave, defined as the b28 & b33 temperament in this limit. Then the lower limit versions were created by simply extrapolating the temperament downwards.
Fomalhaut follows the convention of naming no-twos temperaments after stars.
Subgroup: 3.5.11.13
Comma list: 6655/6561, 274625/264627
Gencom: [3/1 99/65; 6655/6561 274625/264627]
Sval mapping: [⟨1 5 1 -2], ⟨0 -9 3 11]]
POTE generator: ~99/65 = 748.0156
EDTs: b28, b5, b33, b23f, b61, b56f, b38c, b10cf, b66c, b51ff
- Complexity: 1.561892
- Adjusted Error: 6.495941 cents
- TE Error: 1.755451 cents/octave
3.5.11.13.17
Subgroup: 3.5.11.13.17
Comma list: 1105/1089, 4225/4131, 6655/6561
Gencom: [3/1 99/65; 1105/1089 4225/4131 6655/6561]
Sval mapping: [⟨1 5 1 -2 1], ⟨0 -9 3 11 4]]
POTE generator: ~17/11 = 748.0236
EDTs: b28, b5, b33, b23f, b61, b56f, b38c, b10cf, b66c, b51ffg
- Complexity: 1.418914
- Adjusted Error: 6.431616 cents
- TE Error: 1.573498 cents/octave
3.5.11.13.17.19
Subgroup: 3.5.11.13.17.19
Comma list: 247/243, 325/323, 1105/1089, 4675/4617
Gencom: [3/1 99/65; 247/243 325/323 1105/1089 4675/4617]
Sval mapping: [⟨1 5 1 -2 1 7], ⟨0 -9 3 11 4 -11]]
POTE generator: ~17/11 = 747.9960
EDTs: b28, b33, b5, b61, b56f, b23f, b38ch, b66ch, b89fgh, b10cfh
- Complexity: 1.449992
- Adjusted Error: 6.125446 cents
- TE Error: 1.441985 cents/octave
3.5.11.13.17.19.23
Subgroup: 3.5.11.13.17.19.23
Comma list: 209/207, 247/243, 255/253, 325/323, 4675/4617
Gencom: [3/1 99/65; 209/207 247/243 255/253 325/323 4675/4617]
Sval mapping: [⟨1 5 1 -2 1 7 6], ⟨0 -9 3 11 4 -11 -8]]
POTE generator: ~17/11 = 748.0874
EDTs: b28, b5, b33, b23f, b61, b56f, b38ch, b10cfhi, b66ch, b51ffg
- Complexity: 1.382541
- Adjusted Error: 7.087107 cents
- TE Error: 1.566709 cents/octave
Alnilam
Effectively a microtemperament, Alnilam takes a generator of an 81/55 flat fifth and equates 9 of them with 11/9. The name was given by CompactStar to continue with the theme of naming no-twos temperaments after proper star names, but also to indirectly reference mavila.
Subgroup: 3.5.11
Comma list: [0 -35 9 0 10⟩
Gencom: [3/1 81/55; [0 -35 9 0 10⟩]
Sval mapping: [⟨1 5 -1], ⟨0 -10 9]]
CTE generator: ~81/55 = 672.410
EDTs: 99, 17, 82, 116, 181, 65, 14[-5], 280, 48, 215, 31, 133, 314, 263
3.7.11 subgroup temperaments
Mintaka
Extensions to prime 5 are covered at Mintra and Nekkar.
Subgroup: 3.7.11
Comma list: 1331/1323
Sval mapping: [⟨1 0 1], ⟨0 3 2]]
Sval mapping generators: ~3, ~21/11
Supporting ETs: b22, b5, b17, b39, b12, b61, b27, b7, b83, b49, b56, b32, b29, b100
Tridecimal Mintaka
This extension to prime 13 works in the sharper half of the Mintaka tuning range, where the most important pental extension is Mintra.
Subgroup: 3.7.11.13
Comma list: 1331/1323, 218491/216513
Sval mapping: [⟨1 0 1 10], ⟨0 3 2 -13]]
Sval mapping generators: ~3, ~21/11
Supporting ETs: b39, b22, b17, b5f, b61, b56, b100, b139f, b95, b178ef, b83f, b134, b73f, b217ef
Minalzidar
This extension to prime 13 works in the flatter half of the Mintaka tuning range, where the most important pental extension is Nekkar.
Subgroup: 3.7.11.13
Comma list: 1331/1323, 351/343
Sval mapping: [⟨1 0 1 -3], ⟨0 3 2 9]]
Sval mapping generators: ~3, ~21/11
Supporting ETs: b5, b27, b22, b32, b17f, b37f, b12ff, b49, b59, b42df, b76, b39ff, b86d, b71f
Mebsuta
Mebsuta is a microtemperament in the 3.7.11 subgroup that sets the relative sizes of 9/7 and 11/9 to be in the ratio of 5:4; its generator is identifiable as the ratio between these intervals, 81/77. It produces a 21L 1s MOS scale against the tritave, which serves as a well-temperament of 22edt; that scale's chroma is identified with 1331/1323.
Subgroup: 3.7.11
Comma list: 387420489/386683451
Sval mapping: [⟨1 2 2], ⟨0 -5 4]]
Sval mapping generators: ~3, ~81/77
Supporting ETs: b22, b175, b153, b197, b131, b328, b109, b21, b219, b87, b43, b372, b65, b23
3.7.11.19 subgroup
Mebsuta naturally extends itself with prime 19, identifying the two-generator interval as 21/19, since its square differs from 11/9 (the four-generator interval) by the small comma 3971/3969.
Subgroup: 3.7.11.19
Comma list: 3971/3969, 41553/41503
Sval mapping: [⟨1 2 2 3], ⟨0 -5 4 -7]]
Sval mapping generators: ~3, ~81/77
Supporting ETs: b22, b175, b197, b153, b131, b219, b372, b109, b328, b241, b87, b21, b65, b43
3.5.7.11.19 subgroup
Tempering out 12005/11979, the unisquary comma, sets the chroma 1331/1323 equal to 245/243, producing an accurate if complex mapping for prime 5 at 32 generators up; it is notable that this sets eight 11/9s equal to 5/1, which is the 3.5.11 restriction of mohaha.
Subgroup: 3.5.7.11.19
Comma list: 3971/3969, 12005/11979, 41553/41503
Sval mapping: [⟨1 0 2 2 3], ⟨0 32 -5 4 -7]]
Sval mapping generators: ~3, ~81/77
Supporting ETs: b131, b22, b153, b284, b415, b109, b437, b175, b546, b87c, b699, b240, b590, b721
Adhara
Adhara cleaves the step of Mebsuta in three to produce a remarkable Don Page temperament for the chord 7:9:11:13:17 (that is, setting 13/11 to two-thirds of 9/7, and 17/13 to four-thirds of 11/9). It can be extended to even higher subgroups fairly naturally, and encompasses several prominent tunings within its structure (such as 65edt~41edo, 131edt, and 197edt).
Subgroup: 3.7.11.13.17
Comma list: 14161/14157, 107811/107653, 1108809/1108723
Sval mapping: [⟨1 2 2 2 2], ⟨0 -15 12 22 38]]
Sval mapping generators: ~3, ~119/117
Optimal ET sequence: b65, b66, b131, b197, b328, b525, b722, b1247f, b3216defff
3.7.11.13.17.19 subgroup
This includes the natural extension of Mebsuta to prime 19.
Subgroup: 3.7.11.13.17.19
Comma list: 3213/3211, 3971/3969, 14161/14157, 41553/41503
Sval mapping: [⟨1 2 2 2 2 2], ⟨0 -15 12 22 38 -21]]
Sval mapping generators: ~3, ~119/117
Optimal ET sequence: b65, b66, b131, b197, b525, b722, b919, b2035df
3.7.8.11.13.17.19 subgroup
This sets two-thirds of 11/9 to 8/7.
Subgroup: 3.7.8.11.13.17.19
Comma list: 513/512, 729/728, 833/832, 969/968, 3971/3969
Sval mapping: [⟨1 2 2 2 2 2], ⟨0 -15 -7 12 22 38 -21]]
Sval mapping generators: ~3, ~64/63
Optimal ET sequence: b65, b66, b131, b197, b328, b525, b722, b1247âf, b1969ââf (â is the wart for 8.)
3.5.7.8.11.13.17.19.23 subgroup
At slightly lower accuracy, Procyon can be added to the Adhara structure, thereby spanning the entire triple-octave 23-limit.
Subgroup: 3.5.7.8.11.13.17.19.23
Comma list: 361/360, 441/440, 513/512, 729/728, 833/832, 969/968, 1127/1125
Sval mapping: [⟨1 2 2 2 2 2], ⟨0 -35 -15 -7 12 22 38 -21 -75]]
Sval mapping generators: ~3, ~64/63
Optimal ET sequence: b65i, b66i, b131
Other tritave-based subgroups
Aldebaran
Subgroup: 3.5.13
Comma list: 3159/3125
Sval mapping: [⟨1 0 5], ⟨0 1 -2]]
Supporting ETs: 15, 17, 13, 32, 47, 28, 11[-13], 19[+13], 43, 9[-13], 7[-13], 49[+13], 21[+13], 41[-13]
CTE generator: ~5/3 = 887.76
Keladic
Subgroup: 3.7.13
Comma list: 351/343
Sval mapping: [⟨1 1 0], ⟨0 1 3]]
Sval mapping generators: ~3, ~7/3
Supporting ETs: b9, b5, b14, b13, b23, b22, b32, b6f, b31, b19f, b17f, b41, b7ff, b40
Sadalmelik
Subgroup: 3.13.17
Comma list: 85293/83521
Sval mapping: [⟨1 0 2], ⟨0 4 1]]
Sval mapping generators: ~3, ~17/9
Supporting ETs: b12, b5, b7, b17, b29, b19, b41, b53, b31, b65, b22f, b9ff, b77, b43
No-twos-or-threes subgroup temperaments
Antipyth
Subgroup: 5.7.11
Comma list: 859375/823543
Subgroup-val mapping: [⟨1 2 7], ⟨0 1 7]]
Mapping generators: ~5, ~7/25
Optimal tuning (CTE): ~5 = 1\1ed5, ~7/5 = 592.728
Supporting ETs: c14, c5, c19, c33, c47, c9e, c61, c75, c23e, c24e, c52e, c80e, c89e, c37e
Juggernaut
Subgroup: 5.7.11
Comma list: 125/121
Subgroup-val mapping: [⟨2 4 3], ⟨0 1 0]]
Mapping generators: ~11/5, ~7/25
Optimal tuning (CTE): ~11/5 = 1\2ed5, ~7/5 = 582.512
Supporting ETs: c14, c10, c6, c18, c24, c22, c32, c16, c38, c8d, c34, c26d, c46, c52e
Tridecimal juggernaut
Subgroup: 5.7.11.13
Comma list: 125/121, 637/625
Subgroup-val mapping: [⟨2 4 3 0], ⟨0 1 0 -2]]
Mapping generators: ~11/5, ~7/25
Optimal tuning (CTE): ~11/5 = 1\2ed5, ~7/5 = 582.512
Supporting ETs: c10, c14, c6, c24, c34, c16f, c44, c18f, c38, c26f, c54, c64
Graphs
See: Catalog of 3.5.7 subgroup rank two temperaments#Graphs
Projective tuning space diagrams
See: Catalog of 3.5.7 subgroup rank two temperaments#Projective tuning space diagrams