Mintaka
| Mintaka |
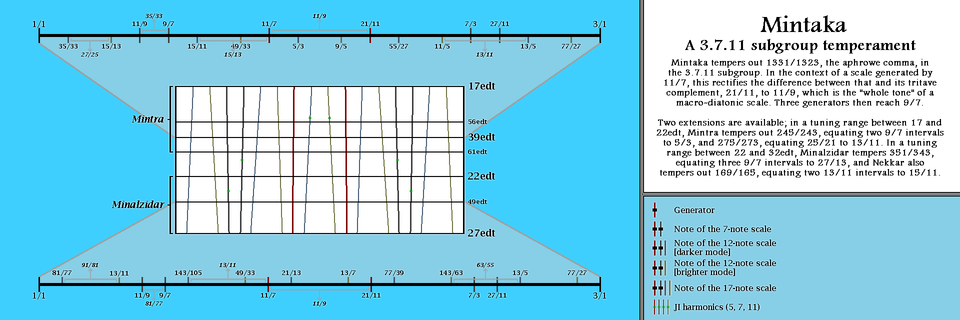
Mintaka is a temperament in the 3.7.11 subgroup where ~11/7 is a generator, and the comma 1331/1323 is tempered out, so a stack of two generators represents 27/11 in addition to 121/49, and a stack of three generators, tritave-reduced, represents 9/7. As 11/7 as a generator against the tritave produces a 5L 2s (macrodiatonic) scale, with the generator here occupying the role of a perfect fourth, it is possible to use an analogue of the chain-of-fifths notation that is standardly used for diatonic scales, with the understanding that sharps are sharper than flats (for example, A♯ is sharper than B♭) and that all intervals are extremely stretched, though the 5L 7s macrochromatic scale is suggested for musical use due to the hardness of the macrodiatonic and the increased breadth of the tritave. 9\22edt is a very good tuning for the generator, and 22edt overall excels in the 3.7.11 subgroup, but other tunings such as 7\17edt and 16\39edt are also useful, especially for extensions involving primes 5 and 13 (see below).
As perhaps the simplest temperament of this subgroup delivering decent accuracy—and, in particular, the simplest supported by tunings such as 17edt and 22edt–Mintaka can be considered the 3.7.11 analog of 3.5.7 BPS or 2.3.5 meantone, using 7:9:11 as its fundamental consonant chord in the place of 3:5:7 or of 4:5:6.
Mos scales of reasonable tunings have cardinalities of 5 (2L 3s), 7 (5L 2s), 12 (5L 7s), or 17 (5L 12s).
For technical data, see No-twos subgroup temperaments#Mintaka.
Extensions of Mintaka
Several extensions of this temperament are possible to incorporate additional harmonics.
Add 23/4 & 20
Off the bat, given that 1331/1323 is a lopsided comma with S-expression S222
- S23, one can reliably choose to temper both S22 = 484/483 and S23 = 529/528 in the 3.7.11.23/4 subgroup, which equates the 11/7 generator to 36/23, and the interval 11/9 to 28/23. Furthermore, the tiny comma S161 = 25921/25920 can be tempered to add harmonic 20 to the subgroup, finding it 8 generators down. More neatly, this can be expressed as the temperament that tempers out the commas 253/252, 484/483, and 540/539 in the 3.7.11.20.23/4 subgroup.
Add 19
Noting that the interval 21/19 is fairly close to the square of 81/77, in tunings near 2/5-comma it is reasonable to temper out 41553/41503 or equivalently 16929/16807 to place 21/19 ten generators up, and the 19th harmonic itself 13 generators down.
Add 13
There are two reasonable ways to incorporate prime 13 into the subgroup. For tunings of the generator sharper than 9\22edt, the step 81/77 approaches or exceeds 260/243 in quality, and therefore can be identified with 260/243 by tempering out 20020/19683, equating 27/13 to (77/81)(20/9), 13 generators down (or alternatively, if one refuses to admit the even number 20 into the subgroup, by tempering out 218491/216513); this is the extension listed as "tridecimal Mintaka". The alternative extension to include prime 13, known as Minalzidar, works better for tunings flatter than 9\22edt, where it is the most accurate to find 13/9 at 3(9/7)−3, 9 generators down, tempering out the comma 351/343. The two representations meet at 22edt.
Add 5
Mintra
| Mintra |
245/243, 275/273, 1331/1323 (3.5.7.11.13)
((13-limited) 25-throdd limit) 8.77c
((13-limited) 25-throdd limit) 39 notes
For tunings of the generator that possess a sharp 9/7 (sharper than 1/3 comma, or effectively between 17edt and 22edt tuning), it is reasonable to combine this temperament with BPS (as well as Deneb in the 3.5.11 subgroup), and additionally temper out 245/243, thereby equating 5/3 to 81/49 at 6 generators up. This is Mintra temperament, which splits the BPS generator in three. A good tuning for this temperament is 39edt, the triple BP equalized scale, though others such as 95edt are possible.
In this range, the "canonical" extension to prime 13 makes sense, though it is worth noting that the Minalzidar extension corresponds directly to the 3.5.7.13 extension of BPS. This extension then is equivalent to tempering out 275/273 and equating 13/11 to 25/21. Furthermore, 13/11 appears 15 generators up, and has a cube root in the temperament: 35/33. Therefore, as 13/11 = (35/33)(37/35)(39/37), it is "free" to equate 35/33 additionally to 37/35 and 39/37 (which amounts to tempering out 407/405), placing the 37th harmonic 8 generators up.
With the inclusion of 20 in the subgroup above, 4/3 would therefore also appear, at the position of (20/9)/(5/3), 14 generators down; though the more interesting case with regard to harmonic 20 is documented below.
Nekkar and Eshurizel
In the flatter generator range (supported by the Minalzidar extension), the optimal representation of 5 is instead that obtained by tempering out 120285/117649, which equates 5 with (529/243)2, placing it 16 generators down; this leads to the 3.5.7.11.13 subgroup version of Nekkar temperament.
Nekkar, as soon as harmonic 20 is inserted, this also equates 5 with (20/9)2, tempering 81/80 in the 3.4.5 subgroup. Furthermore, this then equates 4/3 to 27/20, 8 generators up, therefore creating a square root of 4 at 4 generators up and making this an insane restriction of meantone that must be fixed by including a mapping for 2, which turns out to equate it to the false octave of 243/121 or 99/49. Therefore, as soon as prime 5 is incorporated, this temperament folds into Eshurizel, an elaborate add-19 add-23 extension of 11-limit squares (with commas 81/80, 99/98, and 243/242).
Even without the mappings for other primes, this method can be used to introduce octaves into Mintaka in a manner alike to sensi and hedgehog being produced as extensions of BPS. Equating the false octave (243/121~99/49) to 2/1 provides 2.3.7.11 skwares temperament, to which the aforementioned Eshurizel is but an extension.
Interval chains
One important feature of subgroups involving 3 and 11 is the quasi-octave at the interval designated 243/121; in this temperament, it is equated to 99/49 and placed four generators up. In flatter tunings of the generator, this is closer to a true octave. This interval is meriting of special treatment in terms of consonance and dissonance.
Tritave-reduced harmonics below 243 are marked in bold.
| # | Cents* | Approximate Ratios | |
|---|---|---|---|
| 3.7.11 subgroup | 3.7.11.20.23/4 extension | ||
| −4 | 690.0 | 49/33, 121/81 | 161/108, 180/121 |
| −3 | 1468.5 | 7/3 | 180/77 |
| −2 | 345.0 | 11/9, 147/121 | 28/23, 60/49 |
| −1 | 1123.5 | 21/11, 121/63 | 23/12, 44/23 |
| 0 | 0.0 | 1/1 | 253/252, 484/483, 540/539 |
| 1 | 778.5 | 11/7, 189/121 | 36/23, 69/44 |
| 2 | 1556.9 | 27/11, 121/49 | 69/28, 49/20 |
| 3 | 433.4 | 9/7 | 77/60 |
| 4 | 1211.9 | 99/49, 243/121 | 324/161, 121/60 |
| 5 | 88.4 | 81/77, 363/343 | 207/196, 21/20 |
| 6 | 866.9 | 81/49 | 33/20 |
| 7 | 1645.4 | 891/343, 2187/847 | 207/80 |
| 8 | 521.9 | 729/539 | 759/560, 27/20 |
* In 3.7.11-targeted DKW tuning
Mintra
Good tunings of Mintra lie on the sharper side of the generator range, and include 17edt, 39edt, 56edt, and 95edt.
| # | Cents* | Approximate Ratios | ||
|---|---|---|---|---|
| 3.5.7.11 subgroup | Tridecimal mintra | Add-37 extension | ||
| −6 | 1021.3 | 9/5, 49/27 | 165/91 | |
| −5 | 1802.1 | 77/27, 99/35 | 405/143 | 37/13, 105/37 |
| −4 | 680.9 | 81/55, 49/33, 121/81 | 135/91, 175/117 | 37/25, 273/185 |
| −3 | 1461.7 | 7/3, 81/35 | 275/117 | 333/143 |
| −2 | 340.5 | 11/9, 147/121, 297/245 | 91/75, 175/143 | 111/91, 315/259, 333/275 |
| −1 | 1121.2 | 21/11, 121/63 | 25/13, 143/75 | 333/175, 351/185, 495/259 |
| 0 | 0.0 | 1/1, 245/243 | 275/273 | |
| 1 | 780.8 | 11/7, 189/121 | 39/25 | 175/111, 185/117, 259/165 |
| 2 | 1561.5 | 27/11, 121/49, 245/99 | 225/91, 429/175 | 91/37, 259/105, 275/111 |
| 3 | 440.3 | 9/7, 35/27 | 351/275 | 143/111 |
| 4 | 1221.1 | 55/27, 99/49, 243/121 | 91/45, 351/175 | 75/37, 185/91 |
| 5 | 99.9 | 35/33, 81/77 | 143/135 | 37/35, 39/37, 259/243 |
| 6 | 880.6 | 5/3, 81/49 | 91/55 | |
| 7 | 1661.4 | 55/21 | 13/5 | 259/99, 675/259 |
| 8 | 540.2 | 15/11 | 143/105 | 37/27, 351/259 |
| 9 | 1320.9 | 15/7, 175/81 | 117/55 | 259/121 |
| 10 | 199.7 | 55/49, 135/121, 275/243 | 39/35, 91/81 | 37/33 |
| 11 | 980.5 | 135/77, 175/99 | 143/81 | 37/21 |
| 12 | 1761.2 | 25/9, 135/49 | 91/33 | 333/121 |
| 13 | 640.0 | 175/121, 275/189 | 13/9, 351/245 | 111/77 |
| 14 | 1420.8 | 25/11 | 143/63, 273/121 | 111/49, 185/81 |
| 15 | 299.5 | 25/21 | 13/11 | |
* In 3.5.7.11-subgroup CWE tuning
Tuning spectrum
| Edt Generator |
Eigenmonzo (Unchanged-interval) |
Generator (¢) |
Comments |
|---|---|---|---|
| 7\17 | 783.158 | ||
| 11/7 | 782.492 | 0-comma | |
| 5/3 | 781.378 | in Mintra | |
| 23\56 | 781.160 | ||
| 39\95 | 780.803 | ||
| 28/23 | 780.702 | ||
| 55\134 | 780.653 | ||
| 7/5 | 780.590 | in Mintra | |
| 13/9 | 780.492 | in tridecimal Mintaka | |
| 11/5 | 780.352 | in Mintra | |
| 16\39 | 780.289 | ||
| 13/7 | 780.214 | in tridecimal Mintaka | |
| 13/11 | 780.063 | in tridecimal Mintaka | |
| 57\139 | 779.938 | ||
| 49/33 | 779.883 | 1/4-comma | |
| 41\100 | 779.802 | ||
| 13/5 | 779.732 | in tridecimal Mintra | |
| 25\61 | 779.490 | ||
| 59\144 | 779.273 | ||
| 34\83 | 779.114 | ||
| 9/7 | 779.013 | 1/3-comma | |
| 43\105 | 778.896 | ||
| 52\127 | 778.753 | ||
| 33/20 | 778.478 | ||
| 81/77 | 778.317 | 2/5-comma | |
| 27/20 | 778.177 | ||
| 778.124 | DR 7:9:11, close to 18/43-comma | ||
| 9\22 | 778.073 | ||
| 21/20 | 777.675 | ||
| 11/9 | 777.274 | 1/2-comma | |
| 38\93 | 777.143 | ||
| 29\71 | 776.855 | ||
| 20\49 | 776.308 | ||
| 31\76 | 775.797 | ||
| 49/20 | 775.669 | ||
| 23/12 | 775.636 | ||
| 11\27 | 774.871 | ||
| 121/63 | 772.055 | Full comma |
Other tunings
Scales
- Mintaka7 – 7-note macrodiatonic scale (5L 2s) for 3.7.11 Mintaka
- Mintaka12 – 12-note macrochromatic scale (5L 7s) for 3.7.11 Mintaka
- Mintaka17 – 17-note macroënharmonic scale (5L 12s) for 3.7.11 Mintaka
- Mintra7 – 7-note macrodiatonic scale (5L 2s) for tridecimal Mintra
- Mintra12 – 12-note macrochromatic scale (5L 7s) for tridecimal Mintra
- Mintra17 – 17-note macroënharmonic scale (5L 12s) for tridecimal Mintra
- Mintra22 – 22-note scale (17L 5s) for tridecimal Mintra
Properties and uses
The 7-note scale of Mintaka encompasses the entire (3, 7, 11) tonality diamond in its symmetric mode; as the most consonant chord in the subgroup is 7:9:11, it is useful to speak of modes that have this chord on the tonic, which are those that stack at least three 11/7s up: macro-Dorian (LsLLLsL), Aeolian (LsLLsLL), Phrygian (sLLLsLL), and Locrian (sLLsLLL); the macro-Dorian and Aeolian modes also include the inversion of this chord.
While the macrodiatonic might suffice for the 3.7.11 subgroup, larger scales are needed to represent the primes 5 and 13 in Mintra; the tetrads 5:7:9:11 (~7:9:11:15), 7:9:11:13, and 9:11:13:15 would be bases of harmony in this extended subgroup. In terms of amount of generators (11/7) up from the tonic, these become 0:-9:-6:-8 (~0:3:1:9); 0:3:1:16, and 0:-2:13:6; the 17-note scale therefore includes all tetrads, although not on the same tonic.
Images
A pictorial representation of Mintaka[7], two modes of Mintaka[12], and Mintaka[17], and how they vary across the tuning spectrum, with representative tunings of the two main 13-limit extensions depicted in more detail including approximate JI ratios of each interval.
Music
- Tune in 22edt – Peter Kosmorsky (2011) – uses the LssLssLsssLssLsss MOS (Mintaka[17])