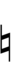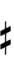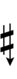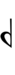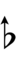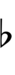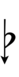41edo

From Xenharmonic Wiki
(Redirected from 82ed4)
Jump to navigation Jump to search
← 40edo 41edo 42edo →
Prime factorization 41 (prime)
Step size 29.2683¢ 
Fifth 24\41 (702.439¢)
(convergent)
Semitones (A1:m2) 4:3 (117.1¢ : 87.8¢)
Consistency limit 15
Distinct consistency limit 9
Special properties
English Wikipedia has an article on:

41 equal divisions of the octave (abbreviated 41edo or 41ed2), also called 41-tone equal temperament (41tet) or 41 equal temperament (41et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 41 equal parts of about 29.3 ¢ each. Each step represents a frequency ratio of 21/41, or the 41st root of 2.

Theory

41edo is the second smallest equal division (after 29edo) whose perfect fifth is closer to just intonation than that of 12edo, and is the seventh zeta integral edo, after 31; it is not, however, a zeta gap edo. This has to do with the fact that it can deal with the 11-limit fairly well, and perhaps the 13-limit. In fact, it is consistent to the 15-odd-limit, or the no-17's 21-odd-limit. All of its intervals between 100 and 1100 cents in size are 15-odd-limit consonances, although its ~13/10 is 14 cents sharp and arguably manifests itself as 21/16 rather than 13/10.

41edo is perhaps the smallest edo with a satisfactory model of the 9-odd-limit, not only because it is the smallest one to tune the 9-odd-limit distinctly consistent, but it is also consistent to distance 2. In other words, all intervals in the 9-odd-limit are more in-tune than out of tune. It is also the first edo to either match or improve on 12edo's accuracy of every harmonic up to the 16th, and no interval from the 11-odd-limit except for 11/10 and 20/11 is represented with more than 10 cents of error in it. Apart from the full 13-limit, it is even more prominent as a 2.3.5.7.11.19.29.31 subgroup temperament for its size.

A step of 41edo is close and consistently mapped to 64/63, the septimal comma.

41edo can be seen as a tuning of the garibaldi temperament[1][2], the magic temperament, the superkleismic temperament and multiple temperaments in the tetracot family. Various 13-limit magic extensions are supported by 41: 13-limit magic, and less successfully necromancy and witchcraft, all merge into one in 41edo tuning. The 41f val provides a superb tuning for sorcery, giving a less-complex version of the 13-limit, and the 41ef val likewise works well for telepathy; telepathy and sorcery merging into one however not in 41edo but in 22edo. 41edo is also a great tetracot tuning, and works as an alternative to 34edo, providing proper approximations to the 7th and 11th harmonic at the cost of the 13th, and supporting monkey, bunya and octacot simultaneously. All three of these extend to the 11-limit by way of interpreting the flat 10/9 as an 11/10 by tempering out 100/99. This equivalence is especially useful in 41edo, wherein this comma-flat whole tone a.k.a. the second of tetracot[7] can also be more accurately interpreted as 21/19 – which is equated with 32/29 above 31/28 below (both very near) — providing an explanation of the accuracy of primes 29 and 31 so that it is a uniquely good/versatile choice for interpreting the harmony of tetracot.

41et is used by the Kite Guitar, see below in #Instruments.

Prime harmonics

Approximation of prime harmonics in 41edo
Harmonic 2 3 5 7 11 13 17 19 23 29 31 37
Error Absolute (¢) +0.0 +0.5 -5.8 -3.0 +4.8 +8.3 +12.1 -4.8 -13.6 -5.2 -3.6 +12.1
Relative (%) +0.0 +1.7 -19.9 -10.2 +16.3 +28.2 +41.4 -16.5 -46.6 -17.7 -12.2 +41.2
Steps
(reduced) 		41
(0) 		65
(24) 		95
(13) 		115
(33) 		142
(19) 		152
(29) 		168
(4) 		174
(10) 		185
(21) 		199
(35) 		203
(39) 		214
(9)
Approximation of prime harmonics in 41edo (continued)
Harmonic 41 43 47 53 59 61 67 71 73 79 83 89
Error Absolute (¢) +10.0 -14.0 +7.7 +4.5 -5.5 -4.7 +8.5 -4.1 +6.4 -13.3 -11.0 +14.5
Relative (%) +34.0 -47.7 +26.2 +15.5 -18.8 -16.0 +29.0 -14.0 +21.7 -45.5 -37.7 +49.5
Steps
(reduced) 		220
(15) 		222
(17) 		228
(23) 		235
(30) 		241
(36) 		243
(38) 		249
(3) 		252
(6) 		254
(8) 		258
(12) 		261
(15) 		266
(20)

Subsets and supersets

41edo is the 13th prime edo, following 37edo and coming before 43edo.

205edo, which slices each step of 41edo into five, corrects some approximations of 41edo to near-just quality. As such, 41edo forms the foundation of the H-System, which uses the scale degrees of 41edo as the basic 13-limit intervals requiring fine tuning +/- 1 average JND from the 41edo circle in 205edo.

Intervals

See also: 41edo solfege
# Cents Approximate Ratios* Ups and Downs Notation SKULO notation (K or S = 1, U = 2) Kite's
Solfege 		Andrew's
Solfege
0 0.00 1/1 perfect unison P1 D perfect unison P1 D Da Do
1 29.27 81/80, 64/63, 49/48 up-unison ^1 ^D comma-wide unison, super unison K1/S1 KD, SD Du Di
2 58.54 25/24, 28/27, 36/35, 33/32 dup-unison, downminor 2nd ^^1, vm2 ^^D, vEb subminor 2nd, classic aug unison, uber unison sm2, kkA1, U1 sEb, kkD#, UD Fro Ro
3 87.80 21/20, 22/21, 19/18, 20/19 down-aug 1sn, minor 2nd vA1, m2 vD#, Eb minor 2nd, comma-narrow augmented unison m2, kA1 Eb, kD# Fra Rih
4 117.07 16/15, 15/14, 14/13 augmented 1sn, upminor 2nd A1, ^m2 D#, ^Eb classic minor 2nd, augmented unison Km2, A1 KEb, D# Fru Ra
5 146.34 12/11, 13/12 mid 2nd ~2 ^D#, vvE neutral second, super augmented unison N2, SA1 UEb/uE, sD# Ri Ru
6 175.61 10/9, 11/10, 21/19 downmajor 2nd vM2 vE classic/comma-wide major 2nd kM2 kE Ro Reh
7 204.88 9/8 major 2nd M2 E major 2nd M2 E Ra Re
8 234.15 8/7, 15/13 upmajor 2nd ^M2 ^E supermajor 2nd SM2 SE Ru Ri
9 263.41 7/6, 22/19 downminor 3rd vm3 vF subminor 3rd sm3 sF No Ma
10 292.68 32/27, 13/11, 19/16 minor 3rd m3 F minor 3rd m3 F Na Meh
11 321.95 6/5 upminor 3rd ^m3 ^F classicminor 3rd Km3 KF Nu Me
12 351.22 11/9, 27/22, 16/13 mid 3rd ~3 ^^F, vGb neutral 3rd, sub diminished 4th N3, sd4 UF/uF#, sGb Mi Mu
13 380.49 5/4, 26/21 downmajor 3rd vM3 vF#, Gb classic major 3rd, diminished 4th kM3, d4 kF#, Gb Mo Mi
14 409.76 81/64, 14/11, 24/19, 19/15 major 3rd M3 F#, ^Gb major 3rd, comma-wide diminished 4th M3, Kd4 F#, KGb Ma Maa
15 439.02 9/7, 32/25 upmajor 3rd ^M3 ^F#, vvG supermajor 3rd, classic diminished 4th SM3, KKd4 SF#, KKGb Mu Mo
16 468.29 21/16, 13/10 down-4th v4 vG sub 4th s4 sG Fo Fe
17 497.56 4/3 perfect 4th P4 G perfect 4th P4 G Fa Fa
18 526.83 27/20, 15/11, 19/14 up-4th ^4 ^G comma-wide 4th K4 KG Fu Fih
19 556.10 11/8, 18/13, 26/19 mid-4th, downdim 5th ~4, vd5 ^^G, vAb uber/neutral 4th, classic augmented 4th U4/N4, kkA4 UG, kkG# Fi/Sho Fu
20 585.37 7/5, 45/32 downaug 4th, dim 5th vA4, d5 vG#, Ab comma-narrow augmented 4th, diminished 5th kA4/d5 kG#, Ab Po/Sha Fi
21 614.63 10/7, 64/45 aug 4th, updim 5th A4, ^d5 G#, ^Ab augmented 4th, comma-wide diminished 5th A4/Kd5 G#, KAb Pa/Shu Se
22 643.90 16/11, 13/9, 19/13 mid-5th, upaug 4th ~5, ^A4 ^G#, vvA unter/neutral 5th, classic diminished 5th u5/N5, KKd5 uA, KKAb Pu/Si Su
23 673.17 40/27, 22/15, 28/19 down-5th v5 vA comma-narrow 5th k5 kA So Sih
24 702.44 3/2 perfect 5th P5 A perfect 5th P5 A Sa Sol
25 731.71 32/21, 20/13 up-5th ^5 ^A super 5th S5 SA Su Si
26 760.98 14/9, 25/16 downminor 6th vm6 ^^A, vBb subminor 6th, classic augmented 5th sm6 sBb, kkA# Flo Lo
27 790.24 128/81, 11/7, 19/12, 30/19 minor 6th m6 vA#, Bb minor 6th, comma-narrow augmented 5th m6 Bb, kA# Fla Leh
28 819.51 8/5, 21/13 upminor 6th ^m6 A#, ^Bb classic minor 6th, augmented 5th Km6, A5 KBb, A# Flu Le
29 848.78 18/11, 44/27, 13/8 mid 6th ~6 ^A#, vvB neutral 6th, super augmented 5th N6 UBb/uB, sA# Li Lu
30 878.05 5/3 downmajor 6th vM6 vB classic major 6th kM6 kB Lo La
31 907.32 27/16, 22/13, 32/19 major 6th M6 B major 6th M6 B La Laa
32 936.59 12/7, 19/11 upmajor 6th ^M6 ^B supermajor 6th SM6 SB Lu Li
33 965.85 7/4, 26/15 downminor 7th vm7 vC subminor 7th sm7 sC Tho Ta
34 995.12 16/9 minor 7th m7 C minor 7th m7 C Tha Teh
35 1024.39 9/5, 20/11, 38/21 upminor 7th ^m7 ^C classic/comma-wide minor seventh Km7 KC Thu Te
36 1053.66 11/6, 24/13 mid 7th ~7 ^^C, vDb neutral 7th, sub diminished 8ve N7 UC/uC#, sDb Ti Tu
37 1082.93 15/8, 28/15, 13/7 downmajor 7th vM7 vC#, Db classic major 7th, diminished 8ve kM7, d8 kC#, Db To Ti
38 1112.20 40/21, 21/11, 36/19, 19/10 major 7th M7 C#, ^Db major 7th, comma-wide diminished 8ve M7, Kd8 C#, KDb Ta Taa
39 1141.46 48/25, 27/14, 35/18, 64/33 upmajor 7th ^M7 C#^, vvD supermajor 7th, classic dim 8ve, unter 8ve SM7, KKd8, U8 SC#, KKDb, u8 Tu To
40 1170.73 160/81, 63/32, 96/49 dim 8ve v8 vD comma-narrow 8ve, sub 8ve k8/s8 kD, sD Do Da
41 1200.00 2/1 perfect 8ve P8 D perfect 8ve P8 D Da Do

* Based on treating 41edo as a 2.3.5.7.11.13.19 subgroup temperament; other approaches are possible.

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality Color Monzo Format Examples
downminor zo (a, b, 0, 1) 7/6, 7/4
minor fourthward wa (a, b) with b < -1 32/27, 16/9
upminor gu (a, b, -1) 6/5, 9/5
mid ilo (a, b, 0, 0, 1) 11/9, 11/6
" lu (a, b, 0, 0, -1) 12/11, 18/11
downmajor yo (a, b, 1) 5/4, 5/3
major fifthward wa (a, b) with b > 1 9/8, 27/16
upmajor ru (a, b, 0, -1) 9/7, 12/7

All 41edo chords can be named using ups and downs. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are. Here are the zo, gu, ilo, yo and ru triads:

Color of the 3rd JI Chord Notes as Edosteps Notes of C Chord Written Name Spoken Name
zo (7-over) 6:7:9 0-9-24 C vEb G Cvm C downminor
gu (5-under) 10:12:15 0-11-24 C ^Eb G C^m C upminor
ilo (11-over) 18:22:27 0-12-24 C vvE G C~ C mid
yo (5-over) 4:5:6 0-13-24 C vE G Cv C downmajor or C down
ru (7-under) 14:18:21 0-15-24 C ^E G C^ C upmajor or C up

Other common triads are

  • 0-10-20 = D F Ab = Dd = D dim
  • 0-10-21 = D F ^Ab = Dd(^5) = D dim up-five
  • 0-10-22 = D F vvA = Dm(~5) = D minor mid-five
  • 0-10-23 = D F vA = Dm(v5) = D minor down-five
  • 0-10-24 = D F A = Dm = D minor
  • 0-14-24 = D F# A = D = D or D major
  • 0-14-25 = D F# ^A = D(^5) = D up-five
  • 0-14-26 = D F# ^^A = D(^^5) = D half-aug
  • 0-14-27 = D F# vA# = Da(v5) = D aug down-five or perhaps D(v#5) = D downsharp-five
  • 0-14-28 = D F# A# = Da = D aug

For a more complete list, see 41edo Chord Names and Ups and Downs Notation #Chords and Chord Progressions.

Notations

Red-Blue Notation

A red-note/blue-note system, similar to the one proposed for 36edo, is one option for notating 41edo. This is a special case of Kite's color notation, treating 41edo as a temperament of the 2,3,7 subgroup. We have the "white key" albitonic notes A-G (7 in total), the "black key" sharps and flats (10 in total), a "red" and "blue" version of each albitonic note (14 in total), a "red" (dark red?) version of each sharp and a "blue" (dark blue?) version of each flat (10 in total), adding up to 41. This would result in quite a colorful keyboard! Note that there are no red flats or blue sharps. Using this nomenclature the notes are:

 A ,  A ,  B♭ ,  B♭ ,  A♯ ,  A♯ ,  B ,  B ,  B ,  C ,  C ,  C ,  D♭ ,  D♭ ,  C♯ ,  C♯ ,  D ,  D ,  D ,  E♭ ,  E♭ ,  D♯ ,  D♯ ,  E ,  E ,  E ,  F ,  F ,  F ,  G♭ ,  G♭ ,  F♯ ,  F♯ ,  G ,  G ,  G ,  A♭ ,  A♭ ,  G♯ ,  G♯ ,  A ,  A 

Interval classes could also be named by analogy. The natural, colorless, or gray interval classes are the Pythagorean ones (which show up in the standard diatonic scale), while "red" and "blue" versions are one step higher or lower. Gray thirds, sixths, and sevenths are usually more dissonant than their colorful counterparts, but the reverse is true of fourths and fifths.

The step size of 41edo is small enough that the smallest interval (the "red/blue unison", seventh-tone, comma, diesis or whatever you want to call it) is actually fairly consonant with most timbres; it resembles a "noticeably out of tune unison" rather than a minor second, and has its own distinct character and appeal.

If "red" is replaced by "up", "blue" by "down", and "neutral" by "mid", and if "gray" is omitted, this notation becomes essentially the same as ups and downs notation. The only difference is the use of minor tritone and major tritone.

Sagittal

From the appendix to The Sagittal Songbook by Jacob A. Barton, a diagram of how to notate 41-EDO in the Revo flavor of Sagittal:

41edo Sagittal.png

Ups and downs notation

41edo can also be notated with quarter-tone accidentals and ups and downs. This can be done by combining sharps and flats with arrows borrowed from extended Helmholtz-Ellis notation:

Step Offset 0 1 2 3 4 5 6 7 8 9
Sharp Symbol
Heji18.svg
Heji19.svg
HeQu1.svg
Heji24.svg
Heji25.svg
Heji26.svg
HeQu3.svg
Heji31.svg
Heji32.svg
Heji33.svg
Flat Symbol
Heji17.svg
HeQd1.svg
Heji12.svg
Heji11.svg
Heji10.svg
HeQd3.svg
Heji5.svg
Heji4.svg
Heji3.svg

The notes within an octave from A are thus:

A, B HeQd3.svg, A HeQu1.svg, B♭, A♯, B HeQd1.svg, A HeQu3.svg, B, C HeQd1.svg, B HeQu1.svg, C, D HeQd3.svg, C HeQu1.svg, D♭, C♯, D HeQd1.svg, C HeQu3.svg, D, E HeQd3.svg, D HeQu1.svg, E♭, D♯, E HeQd1.svg, D HeQu3.svg, E, F HeQd1.svg, E HeQu1.svg, F, G HeQd3.svg, F HeQu1.svg, G♭, F♯, G HeQd1.svg, F HeQu3.svg, G, A HeQd3.svg, G HeQu1.svg, A♭, G♯, A HeQd1.svg, G HeQu3.svg, A

Approximation to JI

Interval mappings

The following table shows how 15-odd-limit intervals are represented in 41edo. Prime harmonics are in bold.

As 41edo is consistent in the 15-odd-limit, the mappings by direct approximation and through the patent val are identical.

15-odd-limit intervals in 41edo
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
3/2, 4/3 0.484 1.7
9/8, 16/9 0.968 3.3
15/14, 28/15 2.370 8.1
7/5, 10/7 2.854 9.8
7/4, 8/7 2.972 10.2
7/6, 12/7 3.456 11.8
13/11, 22/13 3.473 11.9
11/9, 18/11 3.812 13.0
9/7, 14/9 3.940 13.5
11/6, 12/11 4.296 14.7
11/8, 16/11 4.780 16.3
15/8, 16/15 5.342 18.3
5/4, 8/5 5.826 19.9
5/3, 6/5 6.310 21.6
9/5, 10/9 6.794 23.2
13/9, 18/13 7.285 24.9
11/7, 14/11 7.752 26.5
13/12, 24/13 7.769 26.5
13/8, 16/13 8.253 28.2
15/11, 22/15 10.122 34.6
11/10, 20/11 10.606 36.2
13/7, 14/13 11.225 38.4
15/13, 26/15 13.595 46.4
13/10, 20/13 14.079 48.1

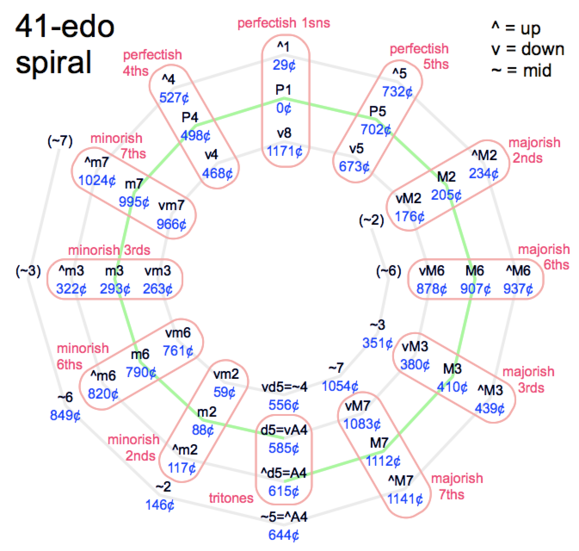
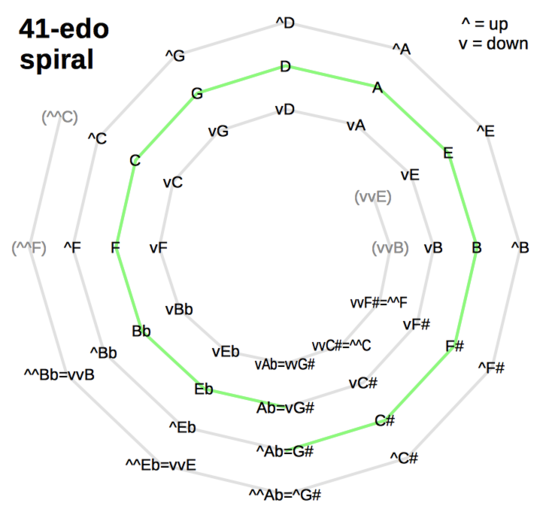
Relationship to 12-edo

Whereas 12edo has a circle of twelve 5ths, 41edo has a spiral of twelve 5ths, since 24\41 is on the 7\12 kite in the scale tree. (See Chapter 5.7 of Kite's book for an explanation of kites.) This spiral of 5th shows 41edo in a 12edo-friendly format. Excellent for introducing 41edo to musicians unfamiliar with microtonal music. There are 12 "-ish" categories, where "-ish" means ±1 edostep. The 6 mid intervals are uncategorized, since they are all so far from 12edo. The two innermost and two outermost intervals on the spiral are duplicates.

41-edo spiral.png

The same spiral, but with notes not intervals:

41-edo spiral with notes.png

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [65 -41⟩ [⟨41 65]] −0.153 0.15 0.52
2.3.5 3125/3072, 20000/19683 [⟨41 65 95]] +0.734 1.26 4.31
2.3.5.7 225/224, 245/243, 1029/1024 [⟨41 65 95 115]] +0.815 1.10 3.76
2.3.5.7.11 100/99, 225/224, 243/242, 245/242 [⟨41 65 95 115 142]] +0.375 1.32 4.51
2.3.5.7.11.13 100/99, 105/104, 144/143, 196/195, 243/242 [⟨41 65 95 115 142 152]] −0.060 1.55 5.29
2.3.5.7.11.13.19 100/99, 105/104, 133/132, 144/143, 171/169, 196/195 [⟨41 65 95 115 142 152 174]] +0.111 1.49 5.10
  • 41et is lower in relative error than any previous equal temperaments in the 3-, 13- and 19-limit. The next equal temperaments doing better in these subgroups are 53, 53, and 46, respectively. It is even more prominent in the 2.3.5.7.11.19 and 2.3.5.7.11.13.19 subgroup. The next equal temperaments doing better in these subgroups are 72 and 53, respectively.

Commas

41edo tempers out the following commas using its patent val, ⟨41 65 95 115 142 152 168 174 185 199 203].

Prime
limit 		Ratio[3] Cents Monzo Color name Name(s)
3 (40 digits) 19.84 [65 -41⟩ Wa-41 41-edo 41-comma
5 (14 digits) 57.27 [-5 -10 9⟩ Tritriyo y9 Shibboleth comma
5 (16 digits) 31.57 [-25 7 6⟩ Lala-tribiyo LLy3 Ampersand
5 3125/3072 29.61 [-10 -1 5⟩ Laquinyo Ly5 Magic comma
5 (10 digits) 27.66 [5 -9 4⟩ Saquadyo sy4 Tetracot comma
5 (18 digits) 25.71 [20 -17 3⟩ Sasa-triyo ssy3 Roda
5 (10 digits) 1.95 [-15 8 1⟩ Layo Ly Schisma
7 (10 digits) 35.37 [0 -7 6 -1⟩ Rutribiyo ry6 Great BP diesis
7 (18 digits) 22.41 [-10 7 8 -7⟩ Lasepru-aquadbiyo Lr7y8 Blackjackisma
7 875/864 21.90 [-5 -3 3 1⟩ Zotriyo zy3 Keema
7 3125/3087 21.18 [0 -2 5 -3⟩ Triru-aquinyo r3y5 Gariboh comma
7 (12 digits) 19.95 [10 -11 2 1⟩ Sazoyoyo szyy Tolerma
7 (10 digits) 16.14 [-15 3 2 2⟩ Labizoyo Lzzyy Mirwomo comma
7 245/243 14.19 [0 -5 1 2⟩ Zozoyo zzy Sensamagic comma
7 4000/3969 13.47 [5 -4 3 -2⟩ Rurutriyo rry3 Octagar comma
7 (12 digits) 9.15 [-15 0 -2 7⟩ Lasepzo-agugu Lz7gg Quince comma
7 1029/1024 8.43 [-10 1 0 3⟩ Latrizo Lz3 Gamelisma
7 225/224 7.71 [-5 2 2 -1⟩ Ruyoyo ryy Marvel comma
7 (10 digits) 6.99 [0 3 4 -5⟩ Quinru-aquadyo r5y4 Mirkwai comma
7 (10 digits) 6.48 [5 -7 -1 3⟩ Satrizo-agu sz3g Hemimage comma
7 5120/5103 5.76 [10 -6 1 -1⟩ Saruyo sry Hemifamity comma
7 (16 digits) 3.80 [25 -14 0 -1⟩ Sasaru ssr Garischisma
7 2401/2400 0.72 [-5 -1 -2 4⟩ Bizozogu z4gg Breedsma
11 (12 digits) 29.72 [15 0 1 0 -5⟩ Saquinlu-ayo s1u5y Thuja comma
11 245/242 21.33 [-1 0 1 2 -2⟩ Luluzozoyo 1uuzzy Frostma
11 100/99 17.40 [2 -2 2 0 -1⟩ Luyoyo 1uyy Ptolemisma
11 1344/1331 16.83 [6 1 0 1 -3⟩ Trilu-azo 1u3z Hemimin comma
11 896/891 9.69 [7 -4 0 1 -1⟩ Saluzo s1uz Pentacircle comma
11 (10 digits) 8.39 [16 0 0 -2 -3⟩ Satrilu-aruru s1u3rr Orgonisma
11 243/242 7.14 [-1 5 0 0 -2⟩ Lulu 1uu Rastma
11 385/384 4.50 [-7 -1 1 1 1⟩ Lozoyo 1ozg Keenanisma
11 441/440 3.93 [-3 2 -1 2 -1⟩ Luzozogu 1uzzg Werckisma
11 1375/1372 3.78 [-2 0 3 -3 1⟩ Lotriruyo 1or3y Moctdel comma
11 540/539 3.21 [2 3 1 -2 -1⟩ Lururuyo 1urry Swetisma
11 3025/3024 0.57 [-4 -3 2 -1 2⟩ Loloruyoyo 1ooryy Lehmerisma
11 (12 digits) 0.15 [-1 2 -4 5 -2⟩ Luluquinzo-aquadgu 1uuz5g4 Odiheim comma
13 343/338 25.42 [-1 0 0 3 0 -2⟩ Thuthutrizo 3uuz3
13 105/104 16.57 [-3 1 1 1 0 -1⟩ Thuzoyo 3uzy Animist comma
13 (10 digits) 14.61 [12 -7 0 1 0 -1⟩ Sathuzo s3uz Secorian comma
13 275/273 12.64 [0 -1 2 -1 1 -1⟩ Thuloruyoyo 3u1oryy Gassorma
13 144/143 12.06 [4 2 0 0 -1 -1⟩ Thulu 3u1u Grossma
13 196/195 8.86 [2 -1 -1 2 0 -1⟩ Thuzozogu 3uzzg Mynucuma
13 640/637 8.13 [7 0 1 -2 0 -1⟩ Thururuyo 3urry Huntma
13 1188/1183 7.30 [2 3 0 -1 1 -2⟩ Thuthuloru 3uu1or Kestrel comma
13 31213/31104 6.06 [-7 -5 0 4 0 1⟩ Thoquadzo 3oz43 Praveensma
13 325/324 5.34 [-2 -4 2 0 0 1⟩ Thoyoyo 3oyy Marveltwin comma
13 352/351 4.93 [5 -3 0 0 1 -1⟩ Thulo 3u1o Major minthma
13 364/363 4.76 [2 -1 0 1 -2 1⟩ Tholuluzo 3o1uuz Minor minthma
13 847/845 4.09 [0 0 -1 1 2 -2⟩ Thuthulolozogu 3uu1oozg Cuthbert comma
13 729/728 2.38 [-3 6 0 -1 0 -1⟩ Lathuru L3ur Squbema
13 2080/2079 0.83 [5 -3 1 -1 -1 1⟩ Tholuruyo 3o1ury Ibnsinma
13 4096/4095 0.42 [12 -2 -1 -1 0 -1⟩ Sathurugu s3urg Schismina
13 6656/6655 0.26 [9 0 -1 0 -3 1⟩ Thotrilo-agu 3u1o3g2 Jacobin comma
13 (10 digits) 0.16 [3 -2 0 -1 3 -2⟩ Thuthutrilo-aru 3uu1o3r Harmonisma
17 2187/2176 8.73 [-7 7 0 0 0 0 -1⟩ Lasu L17u Septendecimal schisma
17 256/255 6.78 [8 -1 -1 0 0 0 -1⟩ Sugu 17ug Charisma
17 715/714 2.42 [-1 -1 1 -1 1 1 -1⟩ Sutholoruyo 17u3o1ory Septendecimal bridge comma
19 210/209 8.26 [1 1 1 1 -1 0 0 -1⟩ Nuluzoyo 19u1uzy Spleen comma
19 361/360 4.80 [-3 -2 -1 0 0 0 0 2⟩ Nonogu 19oog2 Go comma
19 513/512 3.38 [-9 3 0 0 0 0 0 1⟩ Lano L19o Boethius' comma
19 1216/1215 1.42 [6 -5 -1 0 0 0 0 1⟩ Sanogu s19og Eratosthenes' comma
23 736/729 16.54 [5 -6 0 0 0 0 0 0 1⟩ Satwetho s23o Vicesimotertial comma
29 145/144 11.98 [-4 -2 1 0 0 0 0 0 0 1⟩ Twenoyo 29oy 29th-partial chroma

Rank-2 temperaments

Table of temperaments by generator
Degree Cents Temperament(s) Pergen Mos scales
1 29.27 Slendi (P8, P4/17) Pathological 38-tone mos
2 58.54 Hemimiracle
Dodecacot 		(P8, P5/12) 21-tone mos
3 87.80 Octacot (P8, P5/8) 14-tone mos: 3 3 3 3 3 3 3 3 3 3 3 3 3 2
4 117.07 Miracle (P8, P5/6) 11-tone mos: 4 4 4 4 4 4 4 4 4 4 1
5 146.34 BPS / bohpier (P8, P12/13) 20-tone mos
6 175.61 Tetracot / bunya / monkey
Sesquiquartififths / sesquart 		(P8, P5/4) 13-tone mos: 1 5 1 5 1 5 1 5 5 1 5 1 5
7 204.88 Baldy
Quadrimage 		(P8, c3P4/20) 11-tone mos: 6 1 6 6 1 6 1 6 1 6 1
8 234.15 Slendric / rodan / guiron (P8, P5/3) 11-tone mos: 7 1 7 1 7 1 7 1 1 7 1
9 263.41 Septimin (P8, ccP4/11) 9-tone mos: 5 4 5 5 4 5 4 5 4
10 292.68 Quasitemp (P8, c3P4/14) 29-tone mos
11 321.95 Superkleismic (P8, ccP4/9) 11-tone mos: 5 3 5 3 3 5 3 3 5 3 3
12 351.22 Hemif / hemififths / salsa
Karadeniz 		(P8, P5/2) 10-tone mos: 5 2 5 5 2 5 5 5 2 5
13 380.49 Magic / witchcraft
Quanharuk 		(P8, P12/5) 10-tone mos: 2 9 2 2 9 2 2 9 2 2
14 409.76 Hocum
Hocus 		(P8, c3P4/10) 32-tone mos
15 439.02 Superthird (P8, c6P5/18) 11-tone mos: 4 3 4 4 4 3 4 4 3 4 4
16 468.29 Barbad (P8, c7P4/19) 8-tone mos: 7 2 7 7 2 7 7 2
17 497.56 Helmholtz / garibaldi / cassandra / andromeda
Kwai 		(P8, P5) 12-tone mos: 4 3 4 3 3 4 3 4 3 4 3 4 3 3
18 526.83 Trismegistus (P8, c6P5/15) 9-tone mos: 5 5 3 5 5 5 5 3 5
19 556.10 Alphorn (P8, c7P4/16) 9-tone mos: 3 3 3 10 3 3 3 3 10
20 585.37 Pluto
Merman 		(P8, c3P4/7) Pathological 35-tone mos

Scales and modes

Lists of 41edo scales

Harmonic scale

41edo is the first edo to do some justice to Mode 8 of the harmonic series, which Dante Rosati calls the "Diatonic Harmonic Series Scale," consisting of overtones 8 through 16 (sometimes made to repeat at the octave).

Overtones in "Mode 8": 8 9 10 11 12 13 14 15 16
… as JI Ratio from 1/1: 1/1 9/8 5/4 11/8 3/2 13/8 7/4 15/8 2/1
… in cents: 0 203.9 386.3 551.3 702.0 840.5 968.8 1088.3 1200.0
Nearest degree of 41edo: 0 7 13 19 24 29 33 37 41
… in cents: 0 204.9 380.5 556.1 702.4 848.8 965.9 1082.9 1200.0

While each overtone of Mode 8 is approximated within a reasonable degree of accuracy, the steps between the intervals are not uniquely represented. (41edo is, after all, a temperament.)

  • 7\41 (7 degrees of 41edo) (204.9 cents) stands in for just ratio 9/8 (203.9 cents) – a close match.
  • 6\41 (175.6 cents) stands in for both 10/9 (182.4 cents) and 11/10 (165.0 cents).
  • 5\41 (146.3 cents) stands in for both 12/11 (150.6 cents) and 13/12 (138.6 cents).
  • 4\41 (117.1 cents) stands in for 14/13 (128.3 cents), 15/14 (119.4 cents), and 16/15 (111.7 cents).

The scale in 41, as adjacent steps, thus goes: 7 6 6 5 5 4 4 4.

Nonoctave temperaments

Taking every third degree of 41edo produces a scale extremely close to 88cET or 88-cent equal temperament (or the 8th root of 3:2). Likewise, taking every fifth degree produces a scale very close to the equal-tempered Bohlen-Pierce Scale (or the 13th root of 3). See Relationship between Bohlen-Pierce and octave-ful temperaments, and see this chart:

3 degrees of 41edo near 88cET overlap 5 degrees of 41edo near BP
41edo 88cET cents cents cents BP 41edo
0 0 0 0 0
3 1 87.8
146.3 1 5
6 2 175.6
9 3 263.4
292.7 2 10
12 4 351.2
15 5 439.0 3 15
18 6 526.8
585.4 4 20
21 7 614.6
24 8 702.4
731.7 5 25
27 9 790.2
30 10 878.0 6 30
33 11 965.9
1024.4 7 35
36 12 1053.7
39 13 1141.5
1170.7 8 40
[ second octave ]
1 14 29.2
4 15 117.1 9 4
7 16 204.9
263.4 10 9
10 17 292.7
13 18 380.5
409.8 11 14
16 19 468.3
19 20 556.1 12 19
22 21 643.9
702.4 13 24
25 22 731.7
28 23 819.5
848.8 14 29
31 24 907.3
34 25 995.1 15 34
37 26 1082.9
1141.5 16 39
40 27 1170.7
[ third octave ]
2 28 58.5
87.8 17 3
5 29 146.3
8 30 234.1 18 8
11 31 322.0
380.5 19 13
14 32 409.8
17 33 497.6
526.8 20 18
20 34 585.3
23 35 673.2 21 23
26 36 761.0
819.5 22 28
29 37 848.8
32 38 936.6
965.9 23 33
35 39 1024.4
38 40 1112.2 24 38

More scales

Instruments

Guitars

The first 41edo guitar was probably this one, built by Erv Wilson in the 1960's:

Erv Wilson's full-41 guitar 2.jpg

Note the new bridge, several inches below the original bridge. The new bridge increases the scale length and spreads the frets out, making the guitar more playable. Erv numbered the frets as seen here, with the 3-limit dorian scale in enlarged numbers.

Erv Wilson's full-41 guitar 3.jpg

Several more modern guitars:

Melleweijters.com 41edo.jpg

Melle Weijters' 10-string guitar (Melleweijters.com)

41-EDD elektrische gitaar.jpg

41edo electric guitar, by Gregory Sanchez.

Ron_Sword_with_a_41ET_Guitar.jpg

41edo classical guitar, by Ron Sword.

The Kite Guitar (see also KiteGuitar.com and Kite Tuning) is a guitar fretting using every other step of 41edo, i.e. 41ed4 or "20½-edo". However, the interval between two adjacent open strings is always an odd number of 41-edosteps. Thus each string only covers half of 41edo, but the full edo can be found on every pair of adjacent strings. Kite-fretting makes 41edo about as playable as 19edo or 22edo, although there are certain trade-offs.

Caleb's Kite guitar.jpg

For more photos of Kite guitars, see Kite Guitar Photographs.

Keyboards

A possible 41edo keyboard design:

41edo keyboard layout.png

See also 41-edo Keyboards for Lumatone, Linnstrument and Harpejji options, as well as DIY options.

41edo as a Universal Tuning

41's claim to fame as a "universal tuning" is the fact that it approximates scales present in many important world music traditions, and thus is good for both combining and exploring cultural playstyles. It makes no claim to perfectly and faithfully represent the musical cultures listed, as doing so would require far more notes and small details than are present in 41. That being said, it has certain attributes that allow it to approximate common scales in these cultures with far more accuracy than most comparable EDOs.

Western

Due to 41edo's extremely accurate perfect fifth, it makes a good tuning for schismatic temperament and the 12-note MOS, which in turn is a good approximation of the standard 12edo scale, and when arranged as a Bbb-D gamut, approximates the 12-note roughly Pythagorean tuning known as Kirnberger I. This extends the Ptolemy Diatonic Scale (7 6 4 7 6 7 4), which 41 approximates excellently, by completing the circle of fifths with pure 3/2s. By using this system and occasionally substituting in alternate major seconds and sixths when necessary, it becomes quite reminiscent of (and can improve on) 12edo harmony. Additionally, the Pythagorean Pentatonic scale can be used for melodies overtop due to the strong quartal nature of the scale. The Pythagorean diatonic scale exists as an option as well, but use may be limited unless Gentle triads are ideal. An alternate option is approximating a Just Intonation scale such as the Asymmetric scale, a common option for a 5-limit JI scale, or Centaur, a 7-limit JI scale using "blue" or subminor intervals for the accidental notes. There exist other options for 5-limit JI scales, all of which have some reasonable approximation in 41 due to its relative excellence in the 5-limit.

Middle Eastern

See also: Arabic, Turkish, Persian

While the Hemif[7] scale itself and MODMOSes related to it give the middle eastern sound well, 41 has other interesting properties that make it an ideal system for Arabic and Turkish music. It is considered a "Level 2 EDO" due to the fact that it has neutral seconds and thirds as well as submajor and supraminor ones added to a Pythagorean skeleton, with small semitones as minor seconds and major whole tones as major seconds. The submajor third is great for Turkish Rast, around Ozan Yarman’s ideal size, and is sharp enough to sound close to a 5/4, while the neutral third exists as half of a 3/2 and works well for Arabic Rast and some Persian scales. Additionally, a large apotome exists for the Hijaz maqam.

Indonesian

Gamelan music is mainly based on two scales, the older Slendro and newer Pelog, though these scales are expanded on extensively through octave stretching, extensions and combination of the scales, and more. Slendro is excellently approximated by the 8\41 generator. Pelog is approximated quite well also, this time by mavila temperament, using the "grave" fifth of 41 as the generator (23\41).

Indian

See also: Magic22 as srutis

Carnatic music, which is normally based on a 22-note unequal scale, has found some use from 22edo as a good approximation, but 41 offers another option with Magic[22], which not only represents 22edo closely, but preserves accurate perfects fifths and the unequal quality of a more typical carnatic scale. Like any EDO system with an accurate 5-limit and essentially pure fifth, 41 can also approximate a system of Just Shrutis.

Japanese

Japanese classical music known as Gagaku is largely built around winds, strings, and percussion, and the melodies, like many Asian cultures, are built around Pythagorean pentatonic scales, alongside chromaticism with narrow semitones, which are well represented by Pythagorean limmas.

Blues

Due to its pure sounding major thirds and approximations of standard western harmony, 41 naturally is good for jazz and blues music, though a great strength of this system as opposed to many others is its excellent harmonic seventh, alongside MOS scales that supply them, Magic and Miracle in particular.

Coltrane changes can be represented with two Pythagorean major thirds and a pental one, or a temperament like Magic, whose MOSes are characterized by circles of major thirds, giving options for rotating major and minor triads within one scale. Similarly, the Whole Tone scale is represented by Baldy[6], with two pental major thirds and four Pythagorean. This scale can be extended to an 11-note MOS, including a single 4:5:7:9:11 chord and numerous subsets.

Superkleismic presents another option for this purpose, featuring circles of minor thirds, and generating harmonic sevenths with very low complexity.

Blue notes, rather than being considered inflections, can be notated as accidentals instead, such as the "blue third" which is represented by a neutral third, or any number of septimal intervals that are useful in a blues context.

Other

Georgian Polyphonic singing can be done in a 41edo context due to its excellent approximations of prime harmonics and neutral third, as well as Pythagorean seconds and sevenths. Asian musical traditions built around pentatonic scales can use both Pythagorean and Barbad[5].

Music

Modern renderings

Johann Sebastian Bach
Nicolaus Bruhns
Scott Joplin
  • Maple Leaf Rag (1899) – arranged for harpsichord and rendered by Claudi Meneghin (2024)

20th century

Joseph Monzo

21st century

Abnormality
Beheld
Cameron Bobro
Flora Canou
"Chaotic Witch #1" · "Party Cubes" · "Big Dreamer Pavilion" · "Lost Cyclops" · "Sky Tree" · "Long Night Ahead" · "Fractocraft" · "After the Generation"
Francium
Jake Freivald
LΛMPLIGHT
  • Caftaphata (2024) - Also partially in just intonation and 12edo
Ray Perlner
Tapeworm Saga
Chris Vaisvil (site)
Xeno Ov Eleas

Kite Guitar Recordings

Kite Giedraitis
Igliashon Jones
Pixel Archipelago
"Red" · "Orange" · "Yellow" · "Green" · "Blue" · "Indigo" · "Violet"
Aaron Wolf

Kite Guitar Videos

Timmy Barnett
Wilckerson Ganda
Travis Johnson

Kite Guitar Scores

Kite Guitar originals
Kite Guitar translations

See also

External links

Notes

  1. ↑ Schismic Temperaments at x31eq.com, the website of Graham Breed
  2. ↑ Lattices with Decimal Notation at x31eq.com
  3. ↑ Ratios with more than 8 digits are presented by placeholders with informative hints
Retrieved from "https://en.xen.wiki/index.php?title=41edo&oldid=169823"