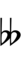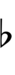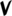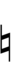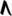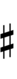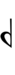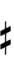31edo
| ← 30edo | 31edo | 32edo → |
31 equal divisions of the octave (abbreviated 31edo or 31ed2), also called 31-tone equal temperament (31tet) or 31 equal temperament (31et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 31 equal parts of about 38.7 ¢ each. Each step represents a frequency ratio of 21/31, or the 31st root of 2.
31edo is also referred to as the tricesimoprimal meantone temperament. The term tricesimoprimal was first used by Adriaan Fokker.
Theory
31edo's perfect fifth is flat of just by 5.2 ¢, as befits a tuning of meantone. The major third is less than a cent sharp of just 5/4, making it slightly sharp of quarter-comma meantone. 31edo's approximation of 7/4, a cent flat, is also very close to just. Because of the near-just 5/4 and 7/4, 31edo is relatively quite accurate in the 7-limit. Many 7-limit JI scales are well-approximated in 31 (with tempering, of course).
Prime 11 is somewhat less accurate, making intervals like 11/8 off by about 9 cents. However, intervals like 11/9 and 11/6 are approximated quite well because the errors cancel out. This makes 31edo a very tone-efficient melodic approximation of the 11-limit (and specifically the 11-odd-limit), although it conflates 9/7 with 14/11 and 11/8 with 15/11. It also maps most 15-odd-limit intervals consistently, the exceptions being 13/9, 13/11, and their octave complements.
Other ways in which 31edo is especially accurate is that it represents a record in Pepper ambiguity in the 7-, 9-, and 11-odd-limit, which it is consistent through. It is also a strict zeta edo, meaning that it is a zeta peak, zeta peak integer, zeta integral, and zeta gap edo all at once.
One step of 31edo, measuring about 38.7 ¢, is called a diesis because it stands in for several intervals called dieses (most notably, 128/125 and 648/625) which are tempered out in 12edo. The diesis is a defining sound of 31edo; when it does not appear directly in a scale, it often shows up as the difference between two or more intervals of a similar size. The diesis is demonstrated in SpiralProgressions. Zhea Erose's 31edo music uses the interval frequently.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -5.2 | +0.8 | -1.1 | -9.4 | +11.1 | +11.2 | +12.2 | -8.9 |
| Relative (%) | +0.0 | -13.4 | +2.0 | -2.8 | -24.2 | +28.6 | +28.9 | +31.4 | -23.0 | |
| Steps (reduced) |
31 (0) |
49 (18) |
72 (10) |
87 (25) |
107 (14) |
115 (22) |
127 (3) |
132 (8) |
140 (16) | |
| Harmonic | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +15.6 | +16.3 | -19.1 | -3.3 | -8.3 | -7.4 | +16.8 | -14.0 | +5.7 |
| Relative (%) | +40.3 | +42.0 | -49.3 | -8.4 | -21.4 | -19.2 | +43.4 | -36.2 | +14.7 | |
| Steps (reduced) |
151 (27) |
154 (30) |
161 (6) |
166 (11) |
168 (13) |
172 (17) |
178 (23) |
182 (27) |
184 (29) | |
As a tuning of other temperaments
Besides meantone, 31edo can be used as a tuning for mohajira, mothra, or less optimally miracle and valentine. These temperaments split 31edo's fifth, at 18 steps, into two, three, six, and nine equal parts. Mohajira and its alternative, called migration, merge in 31edo, and create a near-optimal 11-limit meantone structure in one unified system. In fact, 31edo can be defined as the unique temperament that tempers out 81/80, 99/98, 121/120, and 126/125.
31edo also supports orwell, which splits the perfect twelfth into seven equal parts of ~7/6. Another notable temperament it supports is myna, which divides the category of thirds into five different intervals: subminor, minor, neutral, major, and supermajor, representing 7/6, 6/5, 11/9~16/13, 5/4, and 9/7, respectively.
Subsets and supersets
31edo is the 11th prime edo, following 29edo and coming before 37edo. It does not contain any nontrivial subset edos, though it contains 31ed4. 62edo, which doubles it, provides an alternative way to extend the temperament to the 13- and 17- and 19-limit.
Stretched and compressed tunings
31edo can benefit from slightly stretching the octave, especially when using it as an 11-limit equal temperament. With the right amount of stretch we can find a slightly better 3rd harmonic and significantly better 11th harmonic at the expense of somewhat less accurate approximations of 5, 7, and 13. Tunings such as 80ed6 and 111ed12 are great demonstrations of this.
229ed169 has an octave stretched by 2.23893 ¢. Since the 13th harmonic is exactly halfway between 114 and 115 steps, this difference is the absolute maximum amount of octave stretch 31edo can tolerate before a discrepancy for the 13th harmonic occurs.
Intervals
| Degree | Cents | Approximate ratios[note 1] | Ups and downs notation (EUs: vvA1 and vd2) |
Extended pythagorean notation | SKULO notation (S or U = 1) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1/1 | P1 | perfect unison | D | P1 | perfect unison | D | P1 | perfect unison | D |
| 1 | 38.7 | 45/44, 49/48, 46/45, 128/125, 36/35 | ^1, d2 | up-unison, dim 2nd | ^D, Ebb | d2 | dim 2nd | Ebb | S1/U1 | super/uber unison | SD/UD |
| 2 | 77.4 | 25/24, 21/20, 22/21, 23/22 | A1, vm2 | aug 1sn, downminor 2nd | D#, vEb | A1 | aug 1sn | D# | sm2 | subminor 2nd | sEb |
| 3 | 116.1 | 15/14, 16/15 | m2 | minor 2nd | Eb | m2 | minor 2nd | Eb | m2 | minor 2nd | Eb |
| 4 | 154.8 | 12/11, 11/10, 35/32 | ~2 | mid 2nd | vE | AA1, dd3 | double-aug 1sn, double-dim 3rd | Dx, Fbb | N2 | neutral 2nd | UEb/uE |
| 5 | 193.5 | 9/8, 10/9, 19/17, 28/25 | M2 | major 2nd | E | M2 | major 2nd | E | M2 | major 2nd | E |
| 6 | 232.3 | 8/7, 144/125 | ^M2 | upmajor 2nd | ^E | d3 | dim 3rd | Fb | SM2 | supermajor 2nd | SE |
| 7 | 271.0 | 7/6, 75/64 | vm3 | downminor 3rd | vF | A2 | aug 2nd | E# | sm3 | subminor 3rd | sF |
| 8 | 309.7 | 6/5, 13/11, 25/21 | m3 | minor 3rd | F | m3 | minor 3rd | F | m3 | minor 3rd | F |
| 9 | 348.4 | 11/9, 27/22, 16/13, 60/49, 49/40 | ~3 | mid 3rd | ^F | AA2, dd4 | double-aug 2nd, double-dim 4th | Ex, Gbb | N3 | neutral 3rd | UF/uF# |
| 10 | 387.1 | 5/4 | M3 | major 3rd | F# | M3 | major 3rd | F# | M3 | major 3rd | F# |
| 11 | 425.8 | 9/7, 14/11, 23/18, 32/25 | ^M3 | upmajor 3rd | ^F# | d4 | dim 4th | Gb | SM3 | supermajor 3rd | SF# |
| 12 | 464.5 | 21/16, 64/49, 13/10, 17/13, 125/96 | v4 | down-4th | vG | A3 | aug 3rd | Fx | s4 | sub 4th | sG |
| 13 | 503.2 | 4/3 | P4 | perfect 4th | G | P4 | perfect 4th | G | P4 | perfect 4th | G |
| 14 | 541.9 | 175/128, 11/8, 15/11, 18/13, 26/19 | ^4, ~4 | up-4th, mid 4th | ^G | AA3, dd5 | double-aug 3rd, double-dim 5th | Fx#, Abb | U4/N4 | uber/neutral 4th | UG |
| 15 | 580.6 | 7/5, 45/32, 25/18 | A4, vd5 | aug 4th, downdim 5th | G#, vAb | A4 | aug 4th | G# | A4 | aug 4th | G# |
| 16 | 619.4 | 10/7, 64/45, 36/25 | ^A4, d5 | upaug 4th, dim 5th | ^G#, Ab | d5 | dim 5th | Ab | d5 | dim 5th | Ab |
| 17 | 658.1 | 256/175, 13/9, 16/11, 22/15, 19/13 | v5, ~5 | down-5th, mid 5th | vA | AA4, dd6 | double-aug 4th, double-dim 6th | Gx, Bbbb | u5/N5 | unter/neutral 5th | uA |
| 18 | 696.8 | 3/2 | P5 | perfect 5th | A | P5 | perfect 5th | A | P5 | perfect 5th | A |
| 19 | 735.5 | 32/21, 49/32, 20/13, 26/17, 192/125 | ^5 | up-5th | ^A | d6 | dim 6th | Bbb | S5 | super 5th | SA |
| 20 | 774.2 | 14/9, 11/7, 25/16 | vm6 | downminor 6th | vBb | A5 | aug 5th | A# | sm6 | subminor 6th | sBb |
| 21 | 812.9 | 8/5 | m6 | minor 6th | Bb | m6 | minor 6th | Bb | m6 | minor 6th | Bb |
| 22 | 851.6 | 18/11, 44/27, 13/8, 49/30, 80/49 | ~6 | mid 6th | vB | AA5, dd7 | double-aug 5th, double-dim 7th | Ax, Cbb | N6 | neutral 6th | UBb/uB |
| 23 | 890.3 | 5/3, 42/25 | M6 | major 6th | B | M6 | major 6th | B | M6 | major 6th | B |
| 24 | 929.0 | 12/7, 128/75 | ^M6 | upmajor 6th | ^B | d7 | dim 7th | Cb | SM6 | supermajor 6th | SB |
| 25 | 967.7 | 7/4, 125/72 | vm7 | downminor 7th | vC | A6 | aug 6th | B# | sm7 | subminor 7th | sC |
| 26 | 1006.5 | 16/9, 9/5, 34/19, 25/14 | m7 | minor 7th | C | m7 | minor 7th | C | m7 | minor 7th | C |
| 27 | 1045.2 | 11/6, 20/11, 64/35 | ~7 | mid 7th | ^C | AA6, dd8 | double-aug 6th, double-dim 8ve | Bx, Dbb | N7 | neutral 7th | UC/uC# |
| 28 | 1083.9 | 28/15, 15/8 | M7 | major 7th | C# | M7 | major 7th | C# | M7 | major 7th | C# |
| 29 | 1122.6 | 48/25, 40/21, 21/11, 44/23 | ^M7 | upmajor 7th | ^C# | d8 | dim 8ve | Db | SM7 | supermajor 7th | SC# |
| 30 | 1161.3 | 88/45, 96/49, 45/23, 125/64, 35/18 | v8 | down-8ve | vD | A7 | aug 7th | Cx | s8/u8 | sub 8th, unter 8ve | sD/uD |
| 31 | 1200.0 | 2/1 | P8 | perfect 8ve | D | P8 | perfect 8ve | D | P8 | perfect 8ve | D |
Interval quality and chord names in color notation
Combining ups and downs notation with color notation, qualities can be loosely associated with colors:
| Quality | Color name | Monzo format | Examples |
|---|---|---|---|
| downminor | zo | [a b 0 1⟩ | 7/6, 7/4 |
| minor | fourthward wa | [a b⟩ where b > −1 | 32/27, 16/9 |
| gu | [a b -1⟩ | 6/5, 9/5 | |
| mid | ilo | [a b 0 0 1⟩ | 11/9, 11/6 |
| lu | [a b 0 0 -1⟩ | 12/11, 18/11 | |
| major | yo | [a b 1⟩ | 5/4, 5/3 |
| fifthward wa | [a b⟩ where b > 1 | 9/8, 27/16 | |
| upmajor | ru | [a b 0 -1⟩ | 9/7, 12/7 |
All 31edo chords can be named using ups and downs. Alterations are always enclosed in parentheses, additions never are. An up, down or mid immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Here are the zo, gu, ilo, yo and ru triads:
| Color of the 3rd | JI chord | Edosteps | Notes of C chord | Written name | Spoken name |
|---|---|---|---|---|---|
| zo (7-over) | 6:7:9 | 0 – 7 – 18 | C – vE – G or C – E – G | Cvm | C downminor |
| gu (5-under) | 10:12:15 | 0 – 8 – 18 | C – E – G | Cm | C minor |
| ilo (11-over) | 18:22:27 | 0 – 9 – 18 | C – vE – G or C – E – G | C~ | C mid |
| yo (5-over) | 4:5:6 | 0 – 10 – 18 | C – E – G | C, Cmaj | C, C major |
| ru (7-under) | 14:18:21 | 0 – 11 – 18 | C – ^E – G or C – E – G | C^ | C up, C upmajor |
For a more complete list of chords, see 31edo Chord Names and Ups and downs notation #Chords and chord progressions.
Notation
Ups and downs notation
Spoken as up, sharp, upsharp, etc. Note that up can be respelled as downsharp. The gamut runs D, ^D/vD#, D#, Eb, ^Eb/vE, E, ^E, vF, F etc.
| Step offset | −4 | −3 | −2 | −1 | 0 | +1 | +2 | +3 | +4 |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
|
|
|
|
Neutral chain-of-fifths notation
Since a sharp raises by 2 steps, 31edo can be notated using quarter-tone accidentals. Between C and D (do and re) for example, we have the following notes:
| Degree | Letter | Solfège | English full name |
|---|---|---|---|
| 0 | C | do | C |
| 1 | C |
do |
C half-sharp |
| 2 | C♯ | do ♯ | C sharp |
| 3 | D♭ | re ♭ | D flat |
| 4 | D |
re |
D half-flat |
| 5 | D | re | D |
Stein–Zimmermann accidentals
| Step offset | −4 | −3 | −2 | −1 | 0 | +1 | +2 | +3 | +4 |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
|
|
|
|
Chain-of-fifths notation
Chain-of-fifths notation uses double sharps and double flats only:
| Degree | Letter | Solfège | English full name |
|---|---|---|---|
| 0 | C | do | C |
| 1 | D𝄫 | re 𝄫 | D double flat |
| 2 | C♯ | do ♯ | C sharp |
| 3 | D♭ | re ♭ | D flat |
| 4 | C𝄪 | do 𝄪 | C double sharp |
| 5 | D | re | D |
While using double sharps and double flats may seem confusing because it alternates between C and D, it provides a way of writing chords that is consistent with traditional notation. For example, the subminor7 chord 12:14:18:21 is written like so:
- C / D♯ / G / A♯
- C♯ / D𝄪 / G♯ / A𝄪
- D♭ / E / A♭ / B
- D / E♯ / A / B♯
In 12edo, the enharmonic equivalences include C♯ = D♭, E♯ = F, and E = F♭. But in 31edo we have:
Sagittal notation
This notation uses the same sagittal sequence as edos 17, 24, and 38, and is a subset of the notation for 62edo.
Evo flavor

Revo flavor

We also have a diagram from the appendix to The Sagittal Songbook by Jacob A. Barton, which gives multiple spellings for each pitch, and up to the double-apotome:
Evo-SZ flavor

Because it contains no Sagittal symbols, this Evo-SZ Sagittal notation is identical to Stein–Zimmerman notation.
Relationship to 12edo
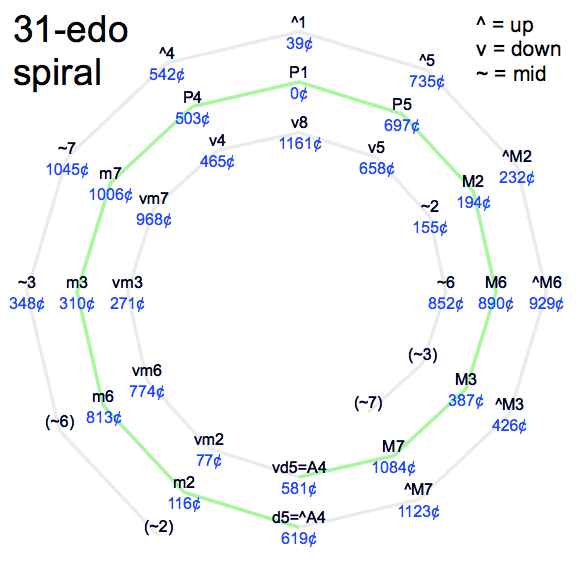
31edo’s circle of 31 fifths can be bent into a 12-spoked "spiral of fifths". In Kite Giedraitis' theory, this is possible because going up 12 fifths in 31edo yields a difference (the absolute value of the dodeca-sharpness) of 1 edostep (which also implies that 18\31 is on the 7\12 kite in the scale tree).
This "spiral of fifths" can be a useful construct for introducing 31edo to musicians unfamiliar with microtonal music. It may help composers and musicians to make visual sense of the notation, and to understand what size of a jump is likely to land them where compared to 12edo.
The two innermost and two outermost intervals on the spiral are duplicates, reflecting the fact that it is a repeating circle at heart and the spiral shape is only a helpful illusion.
Scales
MOS scales
The fact that 31edo has meantone diatonic and chromatic scales is well-known, but some other MOSes and MOS chains[clarification needed] are also useful:
- 9\31, the neutral third, generates ultrasoft mosh and superhard dicotonic MOSes.
- 11\31, the supermajor third or diminished fourth, generates a parahard sensoid scale with resolution from neutral thirds, sixths, and sevenths to perfect fourths, fifths, and octaves, and a semihard 3L 8s scale with a jagged-but-chromatic feel.
- 12\31 generator generates a semihard oneirotonic (5L 3s) scale, similar to the 5L 3s scale in 13edo but with the 9/8, 5/4, and 7/6 better in tune and with the flat fifth close to 19/13.
- A chain of 5\31 whole tones is exceptionally rich in 4:5:7 chords, which are approximated very well in 31edo.
- If you're fond of orwell tetrads (which are also found in 31edo's oneirotonic), you will like the 7\31 (271.0 ¢) subminor third generator. The ultrasoft 9-tone orwelloid 4L 5s MOS could be treated as a 9-tone well temperament.
- It has close approximations to 6edf (→ miracle) and 9edf (→ Carlos Alpha), fifth-equivalent equal divisions that hit many good JI approximations.
See #Rank-2 temperaments for a table of MOSes and their temperament interpretations.
Harmonic scales
31edo approximates Mode 8 of the harmonic series okay, but many intervals between the harmonics aren't distinguished, most importantly 9/8 (major tone) and 10/9 (minor tone), as 31EDO is a meantone temperament. The interval between the 8th and 11th harmonics is approximated okay, but the intervals between the 11th harmonic and closer harmonics such as the 12th and 9th harmonics are approximated much better. 31edo's closest approximation of 13/8, the neutral sixth, is significantly sharper than just and only vaguely suggests the 13-limit.
The steps are: 5 5 4 4 4 3 3 3.
| Overtones in "Mode 8": | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|
| …as JI Ratio from 1/1: | 1/1 | 9/8 | 5/4 | 11/8 | 3/2 | 13/8 | 7/4 | 15/8 | 2/1 |
| …in cents: | 0 | 203.9 | 386.3 | 551.3 | 702.0 | 840.5 | 968.8 | 1088.3 | 1200.0 |
| Nearest degree of 31edo: | 0 | 5 | 10 | 14 | 18 | 22 | 25 | 28 | 31 |
| …in cents: | 0 | 193.5 | 387.1 | 541.9 | 696.8 | 851.6 | 967.7 | 1083.9 | 1200.0 |
In mode 16, the most closely-matched harmonics are the composite ones, 21 and 25. Of the other harmonics:
- 17 is sharp, like 13. In fact, the 17:13 ratio is matched within a tenth of a cent.
- 19 is also sharp, like 13 and 17. The 19:17 ratio is about one cent sharp. 31edo could be considered a tuning of the 2.5.7.13.17.19 subgroup, on which it is consistent (see mercy temperament).
- 23 is about as flat as 11. The chromatic semitone is about half a cent off from 23:22. 31edo could be considered a tuning of the 2.3.5.7.11.23 subgroup, on which it is consistent.
- 27 is quite flat, as it's 33 and the error from the meantone fifths accumulates.
- 29 and 31 are both almost critically sharp, and intervals involving them are unlikely to play any major role.
| Odd overtones in "Mode 16": | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
|---|---|---|---|---|---|---|---|---|
| …as JI Ratio from 1/1: | 17/16 | 19/16 | 21/16 | 23/16 | 25/16 | 27/16 | 29/16 | 31/16 |
| …in cents: | 105.0 | 297.5 | 470.8 | 628.3 | 772.6 | 905.9 | 1029.6 | 1145.0 |
| Nearest degree of 31edo: | 3 | 8 | 12 | 16 | 20 | 23 | 27 | 30 |
| …in cents: | 116.1 | 309.7 | 464.5 | 619.4 | 774.2 | 890.3 | 1045.1 | 1161.3 |
Various subsets
A large open list of subsets from 31edo that people have named:
- 31edo modes
- Strictly proper 7-tone 31edo scales
- Interesting (to somebody) 9-tone 31edo scales
- the Erose–McClain double modes, which are nonoctave
- the Euler–Fokker genus (technically JI but representable in 31)
- the altered pentad
- diasem (2.3.7 subgroup scale; 5 2 5 1 5 2 5 1 5 or 5 1 5 2 5 1 5 2 5 in 31edo)
Approximation to JI
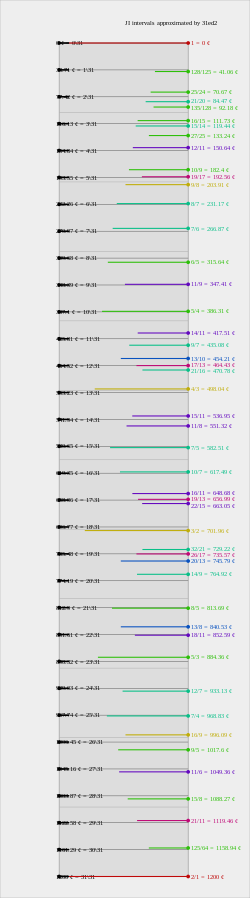
Interval mappings
The following tables show how 15-odd-limit intervals are represented in 31edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 5/4, 8/5 | 0.783 | 2.0 |
| 11/9, 18/11 | 0.979 | 2.5 |
| 7/4, 8/7 | 1.084 | 2.8 |
| 7/5, 10/7 | 1.867 | 4.8 |
| 15/14, 28/15 | 3.314 | 8.6 |
| 7/6, 12/7 | 4.097 | 10.6 |
| 11/6, 12/11 | 4.202 | 10.9 |
| 15/8, 16/15 | 4.398 | 11.4 |
| 15/11, 22/15 | 4.985 | 12.9 |
| 3/2, 4/3 | 5.181 | 13.4 |
| 5/3, 6/5 | 5.964 | 15.4 |
| 11/7, 14/11 | 8.298 | 21.4 |
| 9/7, 14/9 | 9.278 | 24.0 |
| 11/8, 16/11 | 9.382 | 24.2 |
| 11/10, 20/11 | 10.166 | 26.3 |
| 13/10, 20/13 | 10.302 | 26.6 |
| 9/8, 16/9 | 10.362 | 26.8 |
| 13/8, 16/13 | 11.085 | 28.6 |
| 9/5, 10/9 | 11.145 | 28.8 |
| 13/7, 14/13 | 12.169 | 31.4 |
| 15/13, 26/15 | 15.483 | 40.0 |
| 13/12, 24/13 | 16.266 | 42.0 |
| 13/9, 18/13 | 17.263 | 44.6 |
| 13/11, 22/13 | 18.242 | 47.1 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 5/4, 8/5 | 0.783 | 2.0 |
| 11/9, 18/11 | 0.979 | 2.5 |
| 7/4, 8/7 | 1.084 | 2.8 |
| 7/5, 10/7 | 1.867 | 4.8 |
| 15/14, 28/15 | 3.314 | 8.6 |
| 7/6, 12/7 | 4.097 | 10.6 |
| 11/6, 12/11 | 4.202 | 10.9 |
| 15/8, 16/15 | 4.398 | 11.4 |
| 15/11, 22/15 | 4.985 | 12.9 |
| 3/2, 4/3 | 5.181 | 13.4 |
| 5/3, 6/5 | 5.964 | 15.4 |
| 11/7, 14/11 | 8.298 | 21.4 |
| 9/7, 14/9 | 9.278 | 24.0 |
| 11/8, 16/11 | 9.382 | 24.2 |
| 11/10, 20/11 | 10.166 | 26.3 |
| 13/10, 20/13 | 10.302 | 26.6 |
| 9/8, 16/9 | 10.362 | 26.8 |
| 13/8, 16/13 | 11.085 | 28.6 |
| 9/5, 10/9 | 11.145 | 28.8 |
| 13/7, 14/13 | 12.169 | 31.4 |
| 15/13, 26/15 | 15.483 | 40.0 |
| 13/12, 24/13 | 16.266 | 42.0 |
| 13/11, 22/13 | 20.468 | 52.9 |
| 13/9, 18/13 | 21.447 | 55.4 |
Consistent circles
31edo is close to a circle made by stacking 31 pure 17/13 subfourths. A circle of 31 pure 17/13's closes with an error of only 2.74 cents (relative error 7.1%). Remarkably, 31edo tempers out 83521/83486, the 0.7-cent difference between a stack of four 17/13's and a stack of one 19/13 and one 2/1, giving 31edo's oneirotonic (5L 3s) mos accurate 13:17:19 chords.
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-49 31⟩ | [⟨31 49]] | +1.637 | 1.637 | 4.228 |
| 2.3.5 | 81/80, 393216/390625 | [⟨31 49 72]] | +0.976 | 1.628 | 4.204 |
| 2.3.5.7 | 81/80, 126/125, 1029/1024 | [⟨31 49 72 87]] | +0.828 | 1.432 | 3.700 |
| 2.3.5.7.11 | 81/80, 99/98, 121/120, 126/125 | [⟨31 49 72 87 107]] | +1.205 | 1.487 | 3.841 |
| 2.3.5.7.11.13 | 66/65, 81/80, 99/98, 105/104, 121/120 | [⟨31 49 72 87 107 115]] | +0.502 | 2.072 | 5.353 |
| 2.3.5.7.11.23 | 81/80, 99/98, 126/125, 161/160, 231/230 | [⟨31 49 72 87 107 140]] | +1.333 | 1.387 | 3.584 |
- 31et is lower in relative error than any previous equal temperaments in the 7-, 11-, 13-, and 17-limit. The next equal temperaments doing better in those subgroups are 72, 72, 41, and 46, respectively.
- 31et excels in the 2.5.7 subgroup (the JI chord 4:5:7 is represented highly consistently: to distance 10.36). In 2.5.7 it tempers out the didacus comma 3136/3125 and the quince comma 823543/819200, thus also tempering out the very small rainy comma, the simplest 2.5.7 comma tempered out by the 7-limit microtemperament 171edo.
- In the 17-limit it tempers out 120/119, equating the otonal tetrad of 4:5:6:7 and the inversion of the 10:12:15:17 minor tetrad.
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 30.7934 | 30.8119 | 31ddf | ⟨31 49 72 86 107 114] |
| 30.8119 | 30.9423 | 31f | ⟨31 49 72 87 107 114] |
| 30.9423 | 31.0745 | 31 | ⟨31 49 72 87 107 115] |
| 31.0745 | 31.1681 | 31e | ⟨31 49 72 87 108 115] |
| 31.1681 | 31.2125 | 31de | ⟨31 49 72 88 108 115] |
Commas
31et tempers out the following commas. This assumes the val ⟨31 49 72 87 107 115], comma values rounded to 5 significant digits.
| Prime limit |
Ratio[note 2] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | (30 digits) | [-49 31⟩ | 160.605 | Quadlawa | 31-comma |
| 5 | (16 digits) | [-25 7 6⟩ | 31.567 | Lala-tribiyo | Ampersand comma |
| 5 | 81/80 | [-4 4 -1⟩ | 21.506 | Gu | Syntonic comma |
| 5 | (12 digits) | [17 1 -8⟩ | 11.445 | Saquadbigu | Würschmidt comma |
| 5 | (14 digits) | [-21 3 7⟩ | 10.061 | Lasepyo | Semicomma |
| 5 | (24 digits) | [38 -2 -15⟩ | 1.3843 | Sasa-quintrigu | Hemithirds comma |
| 7 | 59049/57344 | [-13 10 0 -1⟩ | 50.72 | Laru | Harrison's comma |
| 7 | 3645/3584 | [-9 6 1 -1⟩ | 29.22 | Laruyo | Schismean comma |
| 7 | (18 digits) | [-10 7 8 -7⟩ | 22.413 | Lasepru-aquadbiyo | Blackjackisma |
| 7 | 64827/64000 | [-9 3 -3 4⟩ | 22.227 | Laquadzo-atrigu | Squalentine comma |
| 7 | 2430/2401 | [1 5 1 -4⟩ | 20.785 | Quadru-ayo | Nuwell comma |
| 7 | 50421/50000 | [-4 1 -5 5⟩ | 14.516 | Quinzogu | Trimyna comma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.795 | Zotrigu | Starling comma, septimal semicomma |
| 7 | 1728/1715 | [6 3 -1 -3⟩ | 13.074 | Trizo-agu | Orwellisma |
| 7 | 1029/1024 | [-10 1 0 3⟩ | 8.4327 | Latrizo | Gamelisma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.7115 | Ruyoyo | Marvel comma, septimal kleisma |
| 7 | 16875/16807 | [0 3 4 -5⟩ | 6.9903 | Quinru-aquadyo | Mirkwai comma |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.0832 | Zozoquingu | Hemimean comma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.3621 | Sarurutrigu | Porwell comma |
| 7 | (18 digits) | [-26 -1 1 9⟩ | 3.7919 | Latritrizo-ayo | Wadisma |
| 7 | 65625/65536 | [-16 1 5 1⟩ | 2.3495 | Lazoquinyo | Horwell comma |
| 7 | (12 digits) | [-11 2 7 -3⟩ | 1.6283 | Latriru-asepyo | Metric comma |
| 7 | 2401/2400 | [-5 -1 -2 4⟩ | 0.72120 | Bizozogu | Breedsma |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.576 | Loruru | Mothwellsma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.367 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.8646 | Lorugugu | Valinorsma |
| 11 | 243/242 | [-1 5 0 0 -2⟩ | 7.1391 | Lulu | Rastma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.5026 | Lozoyo | Keenanisma |
| 11 | 441/440 | [-3 2 -1 2 -1⟩ | 3.9302 | Luzozogu | Werckisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.2090 | Lururuyo | Swetisma |
| 11 | 3025/3024 | [-4 -3 2 -1 2⟩ | 0.57240 | Loloruyoyo | Lehmerisma |
| 13 | 105/104 | [-3 1 1 1 0 -1⟩ | 16.567 | Thuzoyo | Animist comma |
| 13 | 144/143 | [4 2 0 0 -1 -1⟩ | 12.064 | Thulu | Grossma |
| 13 | 196/195 | [2 -1 -1 2 0 -1⟩ | 8.8554 | Thuzozogu | Mynucuma |
| 13 | 351/350 | [-1 3 -2 -1 0 1⟩ | 4.94 | Thorugugu | Ratwolfsma |
| 13 | 352/351 | [5 -3 0 0 1 -1⟩ | 4.93 | Thulo | Minor minthma |
| 13 | 625/624 | [-4 -1 4 0 0 -1⟩ | 2.77 | Thuquadyo | Tunbarsma |
| 13 | 1001/1000 | [-3 0 -3 1 1 1⟩ | 1.73 | Tholozotrigu | Fairytale comma, sinbadma |
| 13 | 4096/4095 | [12 -2 -1 -1 0 -1⟩ | 0.42 | Sathurugu | Schismina |
Rank-2 temperaments
- List of 31et rank two temperaments by badness
- List of edo-distinct 31et rank two temperaments
- Syntonic–31 equivalence continuum
31edo provides the optimal patent val for the rank-5 temperament tempering out the 13-limit comma 66/65, which equates 6/5 and 13/11. It also provides the optimal patent val for mohajira, squares, and casablanca in the 11-limit, and huygens/meantone, squares, winston, lupercalia, and nightengale in the 13-limit.
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
Instruments
Keyboard Instruments
String Instruments
Other Instruments

Lumatone
Skip fretting
Skip fretting system 31 2 9 is a skip fretting system for 31edo.
Skip fretting system 31 3 7 is another skip fretting system for 31edo.
Skip fretting system 31 2 5 is another skip fretting system for 31edo. All examples on this page are for 7-string guitar.
- Prime harmonics
1/1: string 2 open
2/1: string 7 fret 3
3/2: string 4 fret 4
5/4: string 4 open
7/4: string 7 open
11/8: string 4 fret 2
13/8: string 6 fret 1
17/16: string 1 fret 4
19/16: string 2 fret 4
23/16: string 4 fret 3
29/16: string 7 fret 1
31/16: string 1 fret 2
Music
- See also: Category:31edo tracks
See also
- List of 31edo chords
- Pentachords of 31edo
- Tricesimoprimal Tetrachordal Tesseract
- MicroPedagogyCollective – is at work (as of 2012) producing demonstrative material which will encourage and enable more people to learn this system. There have been two ThirtyOneToneSinginCamps as well.
- CG-31
Notes
Further reading
Books
- Coates, Bill. Diesis: An Introduction to the Temperament of 31 Notes to Each Octave. Self-published, 1992.
- Sword, Ron. Tricesimoprimal Scales for Guitar: Scales for 31-EDO. 2009. (Metatonal Music link) (A comprehensive approach to 31edo and all the families associated for guitar. Features over 300 scale charts/scale examples.)
Articles
- The Development of 31-tone Music Permalink by Anton de Beer
- Equal Temperament and the Thirty-one-keyed organ Permalink by Adriaan Daniël Fokker
- New Music with 31 Notes by Adriaan Daniël Fokker, translated by Leigh Gerdine
- About 31-tone Equal Temperament Permalink by Paul Rapoport
- Toward a Theory of Meantone (and 31-et) Harmony Permalink by Siemen Terpstra
- 31-ed2 / 31-edo / 31-ET / 31-tone equal-temperament Permalink on Tonalsoft Encyclopedia
- Harmonic Resources of 31Et EMT and 31EBMT by Juhan Puhm (2016)
External links
Websites
Videos
- Quarter sharps and flats in the same diatonic key signature – Youtube by Stephen Weigel – a list of diatonic key signatures and major scales in 31edo (including semi- and sesqui-sharps); and docs in its description.
- Playlist of 31edo music theory videos on YouTube by Zhea Erose
Software
Diagrams
- Keys and Modes of 31Et by Juhan Puhm (2016)
- Keyboard Mapping for 31Et by Juhan Puhm (2017)
- Mapping Range for 31Et by Juhan Puhm (2017)