Diasem
Diasem (also denoted 2s in groundfault's aberrismic theory) is a 9-note max-variety-3, generator-offset scale with step signature 5L 2m 2s, equivalent to the semiquartal (5L 4s) mos with two of the small steps made larger and the other two made smaller. Diasem is chiral, with two rotationally non-equivalent variants: right-handed (RH) diasem LmLsLmLsL and left-handed (LH) diasem LsLmLsLmL; these step patterns are mirror images. The fact that the small step of diatonic is made smaller results in 26edo and 31edo diasem having better melodic properties than the respective diatonic scales. 21edo is the smallest edo to support a non-degenerate diasem.
Diasem can be tuned as a 2.3.7 subgroup JI scale or a tempered version thereof, where L represents 9/8, m represents 28/27, and s represents 64/63. This interpretation, or more generally the series of generator sequence scales generated by GS(7/6, 8/7) or GS(8/7, 7/6), has been named Tas.
"Diasem" is a name given by groundfault (though others have discussed the scale before her). The name is a portmanteau of "diatonic" and "semiquartal" (or "Semaphore") since its step sizes are intermediate between that of diatonic (5L 2s) and semiquartal (5L 4s); it is also a pun based on the diesis, which appears as the small step in the scale in the 31edo and 36edo tunings.
| Name | Structure | Step Sizes | Graphical Representation |
|---|---|---|---|
| Semiquartal | 5L 4s | 10\62, 3\62 | ├─────────┼──┼─────────┼──┼─────────┼──┼─────────┼──┼─────────┤ |
| Diasem | 5L 2m 2s | 10\62, 4\62, 2\62 | ├─────────┼───┼─────────┼─┼─────────┼───┼─────────┼─┼─────────┤ |
| Diatonic | 5L 2s | 10\62, 6\62 | ├─────────┼─────┼─────────╫─────────┼─────┼─────────╫─────────┤ |
Intervals
The following is a table of diasem intervals and their abstract sizes in terms of L, m and s. Given concrete sizes of L, m and s in edo steps or cents, you can compute the concrete size of any interval in diasem using the following expressions.
| Interval class | Sizes | 2.3.7 JI | 21edo (L:m:s = 3:2:1) | 31edo (L:m:s = 5:2:1) | |
|---|---|---|---|---|---|
| 1-steps | small | s | 64/63, 27.26¢ | 1\21, 57.14¢ | 1\31, 38.71¢ |
| medium | m | 28/27, 62.96¢ | 2\21, 114.29¢ | 2\31, 77.42¢ | |
| large | L | 9/8, 203.91¢ | 3\21, 171.43¢ | 5\31, 193.55¢ | |
| 2-steps | small | L + s | 8/7, 231.17¢ | 4\21, 228.57¢ | 6\31, 232.26¢ |
| medium | L + m | 7/6, 266.87¢ | 5\21, 285.71¢ | 7\31, 270.97¢ | |
| large | 2L | 81/64, 407.82¢ | 6\21, 342.86¢ | 10\31, 387.10¢ | |
| 3-steps | small | L + m + s | 32/27, 294.14¢ | 6\21, 342.86¢ | 8\31, 309.68¢ |
| medium | 2L + s | 9/7, 435.08¢ | 7\21, 400.00¢ | 11\31, 425.81¢ | |
| large | 2L + m | 21/16, 470.78¢ | 8\21, 457.14¢ | 12\31, 464.52¢ | |
| 4-steps | small | 2L + m + s | 4/3, 498.04¢ | 9\21, 514.29¢ | 13\31, 503.23¢ |
| medium | 3L + s | 81/56, 638.99¢ | 10\21, 571.43¢ | 16\31, 619.35¢ | |
| large | 3L + m | 189/128, 674.69¢ | 11\21, 628.57¢ | 17\31, 658.06¢ | |
| 5-steps | small | 2L + m + 2s | 256/189, 525.31¢ | 10\21, 571.43¢ | 14\31, 541.94¢ |
| medium | 2L + 2m + s | 112/81, 561.01¢ | 11\21, 628.57¢ | 15\31, 580.65¢ | |
| large | 3L + m + s | 3/2, 701.96¢ | 12\21, 685.71¢ | 18\31, 696.77¢ | |
| 6-steps | small | 3L + m + 2s | 32/21, 729.22¢ | 13\21, 742.86¢ | 19\31, 735.48¢ |
| medium | 3L + 2m + s | 14/9, 764.92¢ | 14\21, 800.00¢ | 20\31, 774.19¢ | |
| large | 4L + m + s | 27/16, 905.87¢ | 15\21, 857.14¢ | 23\31, 890.32¢ | |
| 7-steps | small | 3L + 2m + 2s | 128/81, 792.18¢ | 15\21, 857.14¢ | 21\31, 812.90¢ |
| medium | 4L + m + 2s | 12/7, 933.13¢ | 16\21, 914.29¢ | 24\31, 929.03¢ | |
| large | 4L + 2m + s | 7/4, 968.83¢ | 17\21, 971.43¢ | 25\31, 967.74¢ | |
| 8-steps | small | 4L + 2m + 2s | 16/9, 996.09¢ | 18\21, 1028.57¢ | 26\31, 1006.45¢ |
| medium | 5L + m + 2s | 54/28, 1137.04¢ | 19\21, 1085.71¢ | 29\31, 1122.58¢ | |
| large | 5L + 2m + s | 63/32, 1172.74¢ | 20\21, 1142.86¢ | 30\31, 1161.29¢ | |
The octave can be called the "perfect 9-step" in TAMNAMS.
Properties
Any diasem scale with positive step sizes has a fifth (large 5-step) between 4\9 (666.67¢) and 3\5 (720¢). The fifth is:
- > 4\7 if L > m + s
- = 4\7 if L = m + s
- < 4\7 if L < m + s
(This can be seen as follows: Let s' = m + s. Then the fifth generates the mos 5L 2s', which is either diatonic, 7edo or antidiatonic depending on the above conditions.)
The scale has two chains of fifth generators (with 5 notes and 4 notes, respectively) with offset L + m or L + s (respectively a flat minor third or a sharp major second in tunings of diasem with "reasonable" fifths and small s steps).
Modes
Diasem has 18 modes, 9 modes of LH diasem and 9 modes of RH diasem. We have provided names based on the modes of the 5L 4s, 5L 2s and 7L 2s temperings of each mode.
Cyclic order
The modes arranged in cyclic order:
| Left-handed modes | Right-handed modes |
|---|---|
| LsLmLsLmL LH Diasem Nucifragan LH Diasem Mixo LH Diasem Superaeolian |
LmLsLmLsL RH Diasem Nucifragan RH Diasem Aeolian RH Diasem Supermixo |
| sLmLsLmLL LH Diasem Pyrrhian LH Diasem Bright Aeolian LH Diasem Superlocrian |
mLsLmLsLL RH Diasem Pyrrhian RH Diasem Locrian RH Diasem Olympian |
| LmLsLmLLs LH Diasem Cornician LH Diasem Dark Aeolian LH Diasem Superionian |
LsLmLsLLm RH Diasem Cornician RH Diasem Ionian RH Diasem Superaeolian |
| mLsLmLLsL LH Diasem Coloean LH Diasem Locrian LH Diasem Corinthian |
sLmLsLLmL RH Diasem Coloean RH Diasem Bright Dorian RH Diasem Superlocrian |
| LsLmLLsLm LH Diasem Stellerian LH Diasem Ionian LH Diasem Superdorian |
LmLsLLmLs RH Diasem Stellerian RH Diasem Dark Dorian RH Diasem Superionian |
| sLmLLsLmL LH Diasem Frugilegian LH Diasem Bright Dorian LH Diasem Superphrygian |
mLsLLmLsL RH Diasem Frugilegian RH Diasem Phrygian RH Diasem Corinthian |
| LmLLsLmLs LH Diasem Pican LH Diasem Dark Dorian LH Diasem Superlydian |
LsLLmLsLm RH Diasem Pican RH Diasem Lydian RH Diasem Superdorian |
| mLLsLmLsL LH Diasem Coracian LH Diasem Phrygian LH Diasem Supermixo |
sLLmLsLmL RH Diasem Coracian RH Diasem Bright Mixo RH Diasem Superphrygian |
| LLsLmLsLm LH Diasem Cristatan LH Diasem Lydian LH Diasem Olympian |
LLmLsLmLs RH Diasem Cristatan RH Diasem Dark Mixo RH Diasem Superlydian |
Arranged by generator chain
When we arrange the modes in the order given by rotating each mode by the generator (the perfect fifth) we obtain the following families of modes (">" roughly means 'brighter than'):
- RH
- LsLLmLsLm (RH Lydian) > LsLmLsLLm (RH Ionian) > sLLmLsLmL (RH Bright Mixo) > sLmLsLLmL (RH Bright Dorian)
- LLmLsLmLs (RH Dark Mixo) > LmLsLLmLs (RH Dark Dorian) > LmLsLmLsL (RH Aeolian) > mLsLLmLsL (RH Phrygian) > mLsLmLsLL (RH Locrian)
- LH
- LLsLmLsLm (LH Lydian) > LsLmLLsLm (LH Ionian) > LsLmLsLmL (LH Mixo) > sLmLLsLmL (LH Bright Dorian) > sLmLsLmLL (LH Bright Aeolian)
- LmLLsLmLs (LH Dark Dorian) > LmLsLmLLs (LH Dark Aeolian) > mLLsLmLsL (LH Phrygian) > mLsLmLLsL (LH Locrian)
This provides a clear motivation for the diatonic-based mode names.
Negative-s blackdye
Consider right-hand diasem, fixing a choice of positive step sizes. There exists a way of superimposing a left-hand diasem mode on the right hand diasem so that the right-hand diasem and the left-hand diasem overlap in 8 notes, yielding a scale of 10 notes, possibly after changing the mode of right-hand diasem. For example, superimposing LmLsLmLsL (RH Aeolian) and LmLsLmLLs (LH Dark Aeolian) gives LmLsLmLs(L-s)s (in fifth-based notation on C: C D Ebv Fv F G Abv Bbv Bb Cv C, where v denotes lowering by s). Note that the union is achiral. This new scale has two chains of perfect fifths each spanning 5 notes:
Chain 1: Bb (L-s)sLmLs F LmLs(L-s)S C LmLsL G mLs(L-s)sL D
Chain 2: Abv Ls(L-s)sLm Ebv LsLmL Bbv S(L-s)sLmL Fv sLmLs(L-s) Cv
Notice that we have two generator chains of equal length. To give this scale a generator-offset structure we can treat the large 7-step as the offset of the 10-note scale. We treat L+S as one scale step and consider the scale an interleaving of two pentatonic scales, using the notes of C-D-F-G-Bb for the even numbered notes and Cv-Ebv-Fv-Abv-Bbv for the odd ones. This gives the following ordering: C Cv D Ebv F Fv G Abv Bb Bbv C, or in step sizes, -s L+s M L+s -s L+s M L+s -s L+s. This is formally a blackdye (sL'mL's'L'mL's'L') pattern, albeit with a negative step size s' = -s! This scale has been called negative blackdye or negative-s blackdye.
Alterations
- Diasem Melodic Minor LmLsLLsLm
In JI and similar tunings
Like Superpyth, JI diasem is great for diatonic melodies in the 2.3.7 subgroup; however, it does not temper 64/63, adding two diesis-sized steps to what would normally be a diatonic scale. Not tempering 64/63 is actually quite useful, because it's the difference between only two 4/3 and a 7/4, so the error is spread over just two perfect fourths. On the other hand, the syntonic comma where the error is spread out over four perfect fifths. As a result, the results of tempering out 81/80 are not as bad, because each fifth only needs to be bent by about half as much to achieve the same optimization for the 5-limit. So in the case of 2.3.7, it may actually be worth it to accept the addition of small step sizes in order to improve tuning accuracy. Another advantage of detempering the septimal comma is that it allows one to use both 9/8 and 8/7, as well as 21/16 and 4/3, in the same scale. Semaphore in a sense does the opposite of what Superpyth does, exaggerating 64/63 to the point that 21/16 is no longer recognizable, and the small steps of diasem become equal to the medium steps.
As a Fokker block
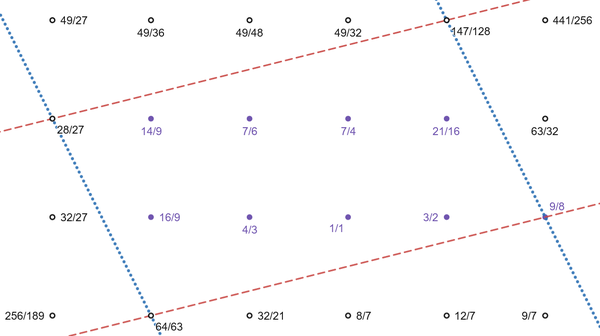
The 2.3.7 JI diasem scale can be viewed as a Fokker block living in the 2.3.7 octave-equivalent pitch class lattice. The x-axis goes along the 3 direction and the y-axis goes along the 7 direction.
The diagram shows the LmLsLmLsL mode. Each dot represents a pitch class of a note in the 2.3.7 lattice. All the notes of the mode are marked as solid purple dots. Notes of the lattice outside the mode are black hollow dots. The red dashed lines are separated by the chroma 49/48, and the blue dotted lines are separated by the chroma 567/512. Note that both 49/48 and 567/512 are tempered out by (the 2.3.7 patent val of) 9edo.
The notes of diasem form the {49/48, 567/512} Fokker block, which is a fundamental domain of the 2.3.7 pitch class lattice; it is possible to tile the entire infinite lattice with copies of right-hand diasem transLated by (49/48)m(567/512)n for integer m and n. Including any one of the other three points on the boundary (28/27, 147/128, or 64/63) instead of 9/8 aLso yields Fokker blocks, more specifically, modes of three of the other domes of diasem, and transLates of the parallelogram that do not have lattice points on the boundary lead to other domes of this Fokker block. However, only one other choice, 28/27, yields a diasem scale, and it yields the left-handed diasem mode mLLsLmLsL.
As a Fokker block, 2.3.7 JI diasem is aLso a product of the tempered 2.3.7 mosses Semaphore[9] (LsLsLsLsL) and septimal Mavila[9] (LLLsLLLsL).
Tunings
| Tuning | L:m:s | Good JI approximations | other comments | Degrees of the mode LmLsLmLsL | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 2.3.7 subgroup interpretation | 9/8 | 7/6 | 21/16 | 4/3 | 3/2 | 14/9 | 7/4 | 16/9 | |||
| JI | 7.479:2.309:1 | Just 7/6, 8/7, and 3/2 | 203.910 | 266.871 | 470.781 | 498.045 | 701.955 | 764.916 | 968.826 | 996.090 | |
| 21edo | 3:2:1 | 16/15, 23/16 and 39/32 | 171.429 | 285.714 | 457.143 | 514.286 | 685.714 | 800 | 971.429 | 1028.571 | |
| 26edo | 4:2:1 | 14/11, 8/7 and 11/8 | 184.615 | 276.923 | 461.538 | 507.692 | 692.308 | 784.615 | 969.231 | 1015.385 | |
| 28edo | 4:3:1 | 5/4 and 13/7 | 171.429 | 300 | 471.429 | 514.286 | 685.714 | 814.286 | 985.714 | 1028.571 | |
| 30edo | 4:3:2 | 13/8 | superdiatonic fifth | 160 | 280 | 440 | 520 | 680 | 800 | 960 | 1040 |
| 31edo | 5:2:1 | Pental thirds and 7/5 | 193.548 | 270.968 | 464.516 | 503.226 | 696.774 | 774.194 | 967.742 | 1006.452 | |
| 33edo | 5:3:1 | 9/7, 13/11 and 10/9 | 181.818 | 290.909 | 472.727 | 509.091 | 690.909 | 763.636 | 981.818 | 1018.182 | |
| 35edo | 5:3:2 | 171.429 | 274.286 | 445.714 | 514.286 | 685.714 | 788.571 | 960 | 1028.571 | ||
| 35edo | 5:4:1 | 171.429 | 308.571 | 480 | 514.286 | 685.714 | 822.857 | 994.286 | 1028.571 | ||
| 36edo | 6:2:1 | Septimal thirds and 3/2 | 200.000 | 266.667 | 466.667 | 500.000 | 700.000 | 766.667 | 966.667 | 1000.000 | |
| 37edo | 5:4:2 | 35/32 | superdiatonic fifth | 162.162 | 291.892 | 454.054 | 518.919 | 681.081 | 810.811 | 972.973 | 1037.838 |
| 38edo | 6:3:1 | 189.474 | 284.2105 | 473.684 | 505.263 | 694.737 | 789.474 | 978.947 | 1010.526 | ||
| 39edo | 5:4:3 | superdiatonic fifth | 153.846 | 276.923 | 430.769 | 523.077 | 676.923 | 800 | 953.846 | 1046.154 | |
| 40edo | 6:3:2 | 180 | 270 | 450 | 510 | 690 | 780 | 960 | 1020 | ||
| 40edo | 6:4:1 | 180 | 300 | 480 | 510 | 690 | 810 | 990 | 1020 | ||
| 41edo | 7:2:1 | 204.878 | 263.415 | 468.293 | 497.561 | 702.439 | 760.976 | 965.854 | 995.122 | ||
| 42edo | 6:5:1 | 171.429 | 314.286 | 485.714 | 514.286 | 685.714 | 828.571 | 1000 | 1028.571 | ||
| 43edo | 7:3:1 | 195.349 | 279.07 | 474.419 | 502.326 | 697.674 | 781.395 | 976.744 | 1004.651 | ||
| 44edo | 6:4:3 | 11/10 (and 9/7) | superdiatonic fifth | 163.636 | 272.727 | 436.364 | 518.182 | 681.818 | 790.909 | 954.5455 | 1036.364 |
| 44edo | 6:5:2 | 11/10 (and 9/7) | superdiatonic fifth | 163.636 | 300 | 463.636 | 518.182 | 681.818 | 818.182 | 981.818 | 1036.364 |
| 45edo | 7:3:2 | 186.667 | 266.667 | 453.333 | 506.667 | 693.333 | 773.333 | 960 | 1013.333 | ||
| 45edo | 7:4:1 | 186.667 | 293.333 | 480 | 506.667 | 693.333 | 800 | 986.667 | 1013.333 | ||
| 46edo | 6:5:3 | Neogothic thirds | superdiatonic fifth | 156.522 | 286.9565 | 443.478 | 521.739 | 678.231 | 808.696 | 965.218 | 1043.418 |
| 46edo | 8:2:1 | Neogothic thirds | gentle fifth | 208.696 | 260.87 | 469.565 | 495.652 | 704.348 | 756.522 | 965.218 | 991.314 |
| 47edo | 7:4:2 | 178.723 | 280.851 | 459.578 | 510.638 | 689.362 | 791.489 | 970.212 | 1021.277 | ||
| 47edo | 7:5:1 | 178.723 | 306.383 | 485.106 | 510.638 | 689.362 | 817.021 | 995.744 | 1021.277 | ||
| 48edo | 6:5:4 | superdiatonic fifth | 150 | 275 | 425 | 525 | 675 | 800 | 950 | 1050 | |
| 48edo | 8:3:1 | superdiatonic fifth | 200 | 275 | 475 | 500 | 700 | 775 | 975 | 1000 | |
| 49edo | 7:4:3 | 171.429 | 269.388 | 440.817 | 514.286 | 685.714 | 783.6735 | 955.102 | 1028.571 | ||
| 49edo | 7:5:2 | 171.429 | 293.878 | 465.756 | 514.286 | 685.714 | 808.163 | 979.592 | 1028.571 | ||
| 49edo | 7:6:1 | 171.429 | 318.367 | 489.796 | 514.286 | 685.714 | 832.653 | 1004.082 | 1028.571 | ||
| 50edo | 8:3:2 | 192 | 264 | 456 | 504 | 696 | 768 | 960 | 1008 | ||
| 50edo | 8:4:1 | 192 | 288 | 480 | 504 | 696 | 792 | 984 | 1008 | ||
| 51edo | 7:5:3 | superdiatonic fifth | 164.706 | 282.353 | 447.059 | 517.647 | 682.353 | 800 | 964.706 | 1035.294 | |
| 51edo | 7:6:2 | superdiatonic fifth | 164.706 | 305.882 | 470.588 | 517.647 | 682.353 | 823.529 | 988.235 | 1035.294 | |
| 52edo | 8:5:1 | 184.615 | 300 | 484.615 | 507.692 | 692.308 | 807.692 | 992.308 | 1015.385 | ||
| 53edo | 7:5:4 | 27/20 | superdiatonic fifth | 158.491 | 271.698 | 429.189 | 520.755 | 679.245 | 792.453 | 950.944 | 1041.509 |
| 53edo | 7:6:3 | 27/20 | superdiatonic fifth | 158.491 | 294.34 | 452.831 | 520.755 | 679.245 | 815.094 | 973.585 | 1041.509 |
Tuning examples
LsLLmLsLm
An example in the RH Diasem Lydian mode LsLLmLsLm. (score)
14edo, L:M:S = 2:1:1 (degenerate; this is basic semiquartal)
16edo, L:M:S = 2:2:1 (degenerate; this is basic superdiatonic)
19edo, L:M:S = 3:1:1 (degenerate; this is hard semiquartal)
21edo, L:M:S = 3:2:1
23edo, L:M:S = 3:2:2 (degenerate; this is soft semiquartal)
24edo, L:M:S = 4:1:1 (degenerate; this is superhard semiquartal)
26edo, L:M:S = 4:2:1
28edo, L:M:S = 4:3:1
31edo, L:M:S = 5:2:1
33edo, L:M:S = 5:3:1
33edo, L:M:S = 5:2:2 (degenerate; this is semihard semiquartal)
35edo, L:M:S = 5:4:1
35edo, L:M:S = 5:3:2
36edo, L:M:S = 6:2:1
38edo, L:M:S = 6:3:1
41edo, L:M:S = 7:2:1
mLsLmLLsL
An example in LH Diasem Locrian mode mLsLmLLsL. (score)
14edo, L:M:S = 2:1:1 (degenerate; this is basic semiquartal)
16edo, L:M:S = 2:2:1 (degenerate; this is basic superdiatonic)
19edo, L:M:S = 3:1:1 (degenerate; this is hard semiquartal)
21edo, L:M:S = 3:2:1
24edo, L:M:S = 4:1:1 (degenerate; this is superhard semiquartal)
26edo, L:M:S = 4:2:1
28edo, L:M:S = 4:3:1
31edo, L:M:S = 5:2:1
33edo, L:M:S = 5:3:1
35edo, L:M:S = 5:4:1
36edo, L:M:S = 6:2:1
38edo, L:M:S = 6:3:1
41edo, L:M:S = 7:2:1
mLLsLmLsL
21edo, L:M:S = 3:2:1
26edo, L:M:S = 4:2:1
31edo, L:M:S = 5:2:1
Supersets
The diasem scale extends to a 14-note generator-offset scale: LmLsLmLsL and LsLmLsLmL both extend to the scale mcmcmsmcmcmsmc (c = L − m), with two 7-note mosses generated by the diasem's fifths separated by m. This scale is not chiral. This scale extends diasem like how blackdye is a 10-note non-chiral generator-offset superset of the Zarlino scale's AG pattern 3L 2m 2s, LmsLmLs. The 14-note superset is one of:
- 5L 7m 2s (if m < c < L)
- a 2-step modmos of 12L 2s (if c = m)
- 7L 5m 2s (if s < c < m)
- 7L 7s (if c = s)
- 7L 2m 5s (if c < s).
5L 7m 2s must have a diatonic fifth, since L > 2m > m + s. The 31edo tuning (c = 3\31, m = 2\31, s = 1\31) of the scale is ideal for the 81/80-tempering 2.3.5.7 interpretation.
Another superset is scscsmscscsmsc, with c = L - s (5L 2m 7s if c > m). 31edo diasem yields 5L 2m 7s with step ratio 4:2:1.
Both these tunings, 5L 7m 2s and 5L 2m 7s, have been named crossdye ("crossed eyes" referring to the two copies of 5L 2s diatonic + "blackdye", courtesy of cellularAutomaton). 5L 7m 2s has been called chromatic crossdye, and 5L 2m 7s has been called dietic crossdye and whitedye.
2.3.7 JI diasem also has the following generator-offset, SV3 supersets:
- a 19-note superset: mLsmsLmsmLsmsLmsmLs (5L 7m 7s), with L = 2187/2048, m = 28/27, and s = 64/63,
- a 29-note superset: mLsmLmLsmLmLmsLmLmLsmLmLmsLmL (12L 12m 5s), with L = 28/27, m = 64/63, and s = 531441/524288.
See also
- Blackdye, a similar diatonic detempering but for 2.3.5
Links
- Play JI diasem - Sevish Scale Workshop
- Play 26edo diasem - Sevish Scale Workshop