Dyadic chord: Difference between revisions
Wikispaces>genewardsmith **Imported revision 266266880 - Original comment: ** |
mNo edit summary |
||
| (137 intermediate revisions by 22 users not shown) | |||
| Line 1: | Line 1: | ||
{{Distinguish| Dyad }} | |||
A '''dyadic chord''', also described as a '''dyadically consonant chord''' or '''pairwise consonant chord''', is a [[chord]] each of whose [[interval]]s belongs to a specified set of intervals considered to be [[consonance and dissonance|consonant]]; it is therefore relative to the set of intervals in question. | |||
For example, the [[tetrad]] | |||
* 1 – 6/5 – 7/5 – 8/5 | |||
is a dyadic chord in the [[7-odd-limit]] since every interval involved in it is an element of the 7-odd-limit [[tonality diamond]]. Now if we replace 7/5 with 10/7: | |||
* 1 – 6/5 – 10/7 – 8/5 | |||
is ''not'' a dyadic chord in the 7-odd-limit. Although each note is 7-odd-limit over the bass, the interval between 10/7 and 6/5 is 25/21, and that between 10/7 and 8/5 is 28/25 – these are not 7-odd-limit. | |||
The significance of dyadic chords and of the paradigm where all interval pairs are examined in the chord has the psychoacoustic basis of timbral fusion and emergence of the [[virtual fundamental]]. In the above examples, it can be shown that the lower harmonics of each note in the first chord blends better than in the second. Meanwhile, the virtual fundamental of the first chord appears 5/1 below the bass, whereas that of the second appears much lower, at 35/1 below the bass as the denominators "fight" each other. For these reasons we tend to find the first chord more consonant than the second. | |||
== Essentially tempered dyadic chord == | |||
[[ | In [[regular temperament theory]], we may speak of a just or tempered dyadic chord. By a ''just'' dyadic chord is meant a chord in just intonation which is dyadic, so that each of its notes in relation to the lowest note is a rational number belonging to the set of consonances, and moreover each interval between the notes belongs to the set of consonances. An ''essentially just'' dyadic chord is a chord which is considered to be an approximation of a just dyadic chord, such that each of its intervals is considered to be an approximation of the corresponding interval in the just dyadic chord. So, for instance, [[4:5:6|1 – 5/4 – 3/2]] is a just dyadic chord when the consonance set is the [[5-odd-limit]] diamond with [[octave equivalence]], and 0 – 10 – 18 in 31edo with consonance set {8, 10, 13, 18, 21, 23, 31} modulo 31 is an essentially just dyadic chord approximating 1 – 5/4 – 3/2. | ||
[[1 | |||
[[ | |||
[[ | |||
[[File:Essentially tempered chord.png|400px|thumb|right|A more in-depth work-through of the starling 1-6/5-10/7 essentially tempered chord example]] | |||
An '''essentially tempered dyadic chord''' is a chord defined in a [[abstract regular temperament|regular temperament]] and relative to a set of consonances such that each interval is within that consonance set, but there is no corresponding just dyadic chord. This means there is no just chord such that each interval, when mapped by the abstract regular temperament, belongs to the consonance set. For example, the chord 1 – 6/5 – 10/7, when mapped by starling temperament, which makes [[126/125]] [[vanish]], has each of its intervals in the set of [[7-odd-limit]] consonances which is the tempering of the 7-odd-limit diamond by 126/125 (this is because 10/7 is off from 36/25 by 126/125, and therefore 10/7 and 36/25 are tempered together in starling temperament, and since 36/25 = (6/5)², the interval from 6/5 to 10/7 in starling may be heard as a second move by 6/5). However, (10/7)/(6/5) = 25/21 is [[25-odd-limit]], and there is no other 7-odd-limit just dyadic chord which can be used instead to give the result, so it is an essentially tempered dyadic chord. | |||
[[ | |||
Essentially tempered dyadic chords are a related notion to [[comma pump]]s, and can be used as a basis for creating pumps. Using essentially tempered chords in chord progressions breaks the harmony out of exclusively just chord relations, and serves as a sort of harmonic lubricant imparting fluidity and dynamism to the harmony, at the cost fairly often of some blurring of the sense of tonality. | |||
[[ | |||
== | == Innate comma chord == | ||
[[ | An '''innate comma chord''', proposed by [[Kite Giedraitis]], is the type of chord that cannot be mapped to just intonation in a given prime limit and odd limit. However, instead of specifying the targeted JI ratios as in an [[#Essentially_tempered_dyadic_chord|essentially tempered chord]], an innate comma chord describes only the general chord shape: the [[mapped interval]] representations or the [[interval span|sizes]] of its constituent intervals. For example, the [[augmented triad]] in 5-limit JI is an innate comma chord below the 25-odd-limit, because it is impossible to tune all three major thirds (in the four-note chord doubling the root up an octave) to [[5/4]] or any other 5-limit interval with odd limit below 25: the innate comma here is 128/125 (41¢). In practice, it might be sung or played justly but with a large odd limit (containing [[wolf interval]]s): for example, 1–5/4–8/5–2, or 1–5/4–25/16–2 (or even 1–5/4–25/16–125/64). Or it might be tempered, e.g. in 12edo as 0¢–400¢–800¢–1200¢. In 7-limit JI, one of the major thirds can be tuned to 9/7, reducing the innate comma to 225/224 (only 8¢). This comma can be distributed among the three thirds, tempering each by only a few cents, which is usually close enough to be acceptable. In 11-limit JI, the augmented chord is not an innate comma chord, because it can be tuned justly as 7:9:11:14, a low enough odd limit to "ring". (However, it is debatable whether this chord qualifies as an augmented triad, because the middle [[11/9]] interval is a neutral third rather than a major third.) | ||
[[ | |||
[[ | |||
[[ | |||
[[ | |||
[[ | |||
[[ | |||
[[ | |||
== | == Anomalous saturated suspension == | ||
[[ | An '''anomalous saturated suspension''' ('''ASS'''), introduced by [[Graham Breed]]<ref>[https://www.webcitation.org/60VBgPSUS ''Anomalous Saturated Suspensions'']</ref>, is a ''q''-odd-limit just dyadic chord to which no pitch ''q''-odd-limit pitch class can be added while keeping it in the ''q''-odd-limit, and which is neither an otonal or a utonal chord; that is, it is not contained as a subchord of either the 1:3:5:…:''q'' chord or the 1:1/3:1/5:…:1/''q'' chord. The existence of such chords was discovered by [[Paul Erlich]]<ref>[https://www.webcitation.org/60VCUHe6d ''Anomalous Saturated Suspensions -- Paul Erlich's post'']</ref>. Below are listed two 9-odd-limit ASSes of special interest, as they avoid intervals smaller than a minor whole tone. | ||
[ | |||
[[ | |||
[ | |||
* [[12:15:18:20]] | |||
[[ | * [[12:14:18:21]] | ||
[[ | |||
For a complete list of ASS chords through the 23-odd-limit see [[List of anomalous saturated suspensions]]. | |||
[[ | |||
== | == List of just intonation tetrads == | ||
[[ | * [[Seven limit tetrads]] | ||
* [[Nine limit tetrads]] | |||
* [[1-3-7-11 tetrads]] | |||
* [[Thirteen limit tetrads]] | |||
* [[Fifteen limit tetrads]] | |||
* [[Seventeen limit tetrads]] | |||
== List of essentially tempered dyadic chords == | |||
Here are some pages on certain essentially tempered dyadic chords, sorted by the lowest odd limit in which they are available. See [[Dyadic chord/Pattern of essentially tempered chords]] for some notable abstract chord patterns. | |||
=== 7-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Archytas chords]] || [[Archytas clan|Archytas]] || [[64/63]] | |||
|- | |||
| [[Starling chords]] || [[Starling]] || [[126/125]] | |||
|} | |||
=== 9-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Didymic chords]] || [[Meantone]] || [[81/80]] | |||
|- | |||
| [[Marvel chords]] || [[Marvel]] || [[225/224]] | |||
|- | |||
| [[Sensamagic chords]] || [[Sensamagic]] || [[245/243]] | |||
|} | |||
=== 11-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Mothwellsmic chords]] || [[Mothwellsmic]] || [[99/98]] | |||
|- | |||
| [[Ptolemismic chords]] || [[Ptolemismic]] || [[100/99]] | |||
|- | |||
| [[Biyatismic chords]] || [[Biyatismic]] || [[121/120]] | |||
|- | |||
| [[Valinorsmic chords]] || [[Valinorsmic]] || [[176/175]] | |||
|- | |||
| [[Rastmic chords]] || [[Rastmic]] || [[243/242]] | |||
|- | |||
| [[Frostmic chords]] || [[Frostmic]] || [[245/242]] | |||
|- | |||
| [[Keenanismic chords]] || [[Keenanismic]] || [[385/384]] | |||
|- | |||
| [[Werckismic chords]] || [[Werckismic]] || [[441/440]] | |||
|- | |||
| [[Swetismic chords]] || [[Swetismic]] || [[540/539]] | |||
|- | |||
| [[Pentacircle chords]] || [[Pentacircle]] || [[896/891]] | |||
|- | |||
| [[Undecimal marvel chords]] || [[Marvel]] || 225/224, 385/384 | |||
|- | |||
| [[Prodigy chords]] || [[Prodigy]] || 225/224, 441/440 | |||
|- | |||
| [[Undecimal sensamagic chords]] || [[Sensamagic]] || 245/243, 385/384 | |||
|- | |||
| [[Jove chords]] || [[Jove]] || 243/242, 441/440 | |||
|- | |||
| [[Miracle chords]] || [[Miracle]] || 225/224, 243/242, 385/384 | |||
|- | |||
| [[Magic chords]] || [[Magic]] || 100/99, 225/224, 245/243 | |||
|- | |||
| [[Supermagic chords]] || [[Supermagic]] || 100/99, 385/384 | |||
|- | |||
| [[Orwell tetrad]] || [[Guanyin]] || 176/175, 540/539 | |||
|- | |||
| [[Tutonic hexad|Tutonic hexads]] || [[Meantone]] || 81/80, 99/98, 126/125 | |||
|- | |||
| [[Baldanders chords|Baldanders hexads]] || [[Andromeda]] || 100/99, 225/224, 245/242 | |||
|- | |||
| [[Porcupine heptad]] || [[Porkypine]] || 55/54, 100/99 | |||
|} | |||
=== 13-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Buzurgismic chords]] || [[Buzurgismic]] || [[169/168]] | |||
|- | |||
| [[Mynucumic chords]] || [[Mynucumic]] || [[196/195]] | |||
|- | |||
| [[Gassormic chords]] || [[Gassormic]] || [[275/273]] | |||
|- | |||
| [[Marveltwin chords]] || [[Marveltwin]] || [[325/324]] | |||
|- | |||
| [[Ratwolfsmic chords]] || [[Ratwolfsmic]] || [[351/350]] | |||
|- | |||
| [[Major minthmic chords]] || [[Major minthmic]] || [[352/351]] | |||
|- | |||
| [[Minor minthmic chords]] || [[Minor minthmic]] || [[364/363]] | |||
|- | |||
| [[Huntmic chords]] || [[Huntmic]] || [[640/637]] | |||
|- | |||
| [[Squbemic chords]] || [[Squbemic]] || [[729/728]] | |||
|- | |||
| [[Cuthbert chords]] || [[Cuthbert]] || [[847/845]] | |||
|- | |||
| [[Sinbadmic chords]] || [[Sinbadmic]] || [[1001/1000]] | |||
|- | |||
| [[Kestrel chords]] || [[Kestrel]] || [[1188/1183]] | |||
|- | |||
| [[Catadictmic chords]] || [[Catadictmic]] || [[1287/1280]] | |||
|- | |||
| [[Lambeth chords]] || [[Lambeth]] || [[1573/1568]] | |||
|- | |||
| [[Petrmic chords]] || [[Petrmic]] || [[2200/2197]] | |||
|- | |||
| [[Rastmic chords #Rastgross heptad|Rastgross heptad]] || [[Namo]] || 144/143, 243/242 | |||
|- | |||
| [[Parapyth chords]] || [[Parapyth]], [[gentle]] || 352/351, 364/363 | |||
|- | |||
| [[Hecate hexad]] || [[Hecate]] || 225/224, 325/324, 385/384 | |||
|- | |||
| [[Woodpecker octad]] || [[Woodpecker]] || 66/65, 121/120, 126/125 | |||
|- | |||
| [[Miraculous decad]] || [[Miraculous]], [[Revelation]] || 105/104, 196/195, 512/507 | |||
|} | |||
=== 15-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Island chords]] || [[The Archipelago|Island]] || [[676/675]] | |||
|- | |||
| [[Nicolic chords]] || [[Nicolic]] || [[1575/1573]] | |||
|- | |||
| [[Myhemiwell chords]] || [[Myhemiwell]] || [[3388/3375]] | |||
|- | |||
| [[Battaglia chord]] || [[Marvel]] || 225/224 | |||
|- | |||
| [[Tetracot chords]] || [[Tetracot]] || 100/99, 243/242 | |||
|- | |||
| [[Orwell tetrad|Orwell ennead]] || [[Guanyin]] || 176/175, 540/539 | |||
|} | |||
=== 17-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Augustmic chords]] || [[Augustmic]] || [[154/153]] | |||
|- | |||
| [[Charismic chords]] || [[Charismic]] || [[256/255]] | |||
|- | |||
| [[Prototannismic chords]] || [[Prototannismic]] || [[273/272]] | |||
|- | |||
| [[Ursulismic chords]] || [[Ursulismic]] || [[375/374]] | |||
|- | |||
| [[Seminaiadmic chords]] || [[Seminaiadmic]] || [[442/441]] | |||
|- | |||
| [[Monardismic chords]] || [[Monardismic]] || [[561/560]] | |||
|- | |||
| [[Dakotismic chords]] || [[Dakotismic]] || [[595/594]] | |||
|- | |||
| [[September chords]] || [[September]] || [[715/714]] | |||
|- | |||
| [[Horizmic chords]] || [[Horizmic]] || [[833/832]] | |||
|- | |||
| [[Ainismic chords]] || [[Ainismic]] || [[936/935]] | |||
|- | |||
| [[Twosquare chords]] || [[Twosquare]] || [[1089/1088]] | |||
|- | |||
| [[Quadrantonismic chords]] || [[Quadrantonismic]] || [[1156/1155]] | |||
|- | |||
| [[Cimbrismic chords]] || [[Cimbrismic]] || [[1275/1274]] | |||
|- | |||
| [[Fidesmic chords]] || [[Fidesmic]] || [[2025/2023]] | |||
|- | |||
| [[Heptacircle chords]] || [[Heptacircle]] || [[2431/2430]] | |||
|- | |||
| [[Sextantonismic chords]] || [[Sextantonismic]] || [[2601/2600]] | |||
|} | |||
=== 19-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Photismic chords]] || [[Photismic]] || [[324/323]] | |||
|- | |||
| [[Nutrismic chords]] || [[Nutrismic]] || [[343/342]] | |||
|- | |||
| [[Dudon chords]] || [[Dudon]] || [[361/360]] | |||
|- | |||
| [[Devichromic chords]] || [[Devichromic]] || [[400/399]] | |||
|- | |||
| [[Abnobismic chords]] || [[Abnobismic]] || [[456/455]] | |||
|- | |||
| [[Hedwigmic chords]] || [[Hedwigmic]] || [[476/475]] | |||
|- | |||
| [[Eulalismic chords]] || [[Eulalismic]] || [[495/494]] | |||
|- | |||
| [[Boethius chords]] || [[Boethius]] || [[513/512]] | |||
|- | |||
| [[Kingfisher chords]] || [[Kingfisher]] || [[969/968]] | |||
|- | |||
| [[Bihendrixmic chords]] || [[Bihendrixmic]] || [[1083/1078]] | |||
|- | |||
| [[Eratosthenes chords]] || [[Eratosthenes]] || [[1216/1215]] | |||
|- | |||
| [[Solvejgsmic chords]] || [[Solvejgsmic]] || [[1331/1330]] | |||
|- | |||
| [[Aureusmic chords]] || [[Aureusmic]] || [[1445/1444]] | |||
|- | |||
| [[Pinkanberry chords]] || [[Pinkanberry]] || [[1521/1520]] | |||
|- | |||
| [[Kevolismic chords]] || [[Kevolismic]] || [[1540/1539]] | |||
|- | |||
| [[Ramanujanismic chords]] || [[Ramanujanismic]] || [[1729/1728]] | |||
|- | |||
| [[Blumeyer chords]] || [[Blumeyer]] || [[2432/2431]] | |||
|- | |||
| [[Neovulturismic chords]] || [[Neovulturismic]] || [[2926/2925]] | |||
|- | |||
| [[Neomirkwaismic chords]] || [[Neomirkwaismic]] || [[3136/3135]] | |||
|- | |||
| [[Neosatanismic chords]] || [[Neosatanismic]] || [[4200/4199]] | |||
|- | |||
| [[Langwismic chords]] || [[Langwismic]] || [[6144/6137]] | |||
|} | |||
=== 21-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Slendric pentad]] || [[Gamelismic clan|Gamelismic]] || [[1029/1024]] | |||
|- | |||
| [[Palingenetic chords]] || [[Palingenetic]] || [[1701/1700]] | |||
|- | |||
| [[Xenismic chords]] || [[Xenismic]] || [[2058/2057]] | |||
|- | |||
| [[Ibnsinmic chords]] || [[Ibnsinmic]] || [[2080/2079]] | |||
|- | |||
| [[Heartlandismic chords]] || [[Heartlandismic]] || [[3971/3969]] | |||
|- | |||
| [[Schisminic chords]] || [[Schisminic]] || [[4096/4095]] | |||
|- | |||
| [[Baladismic chords]] || [[Baladismic]] || [[4914/4913]] | |||
|- | |||
| [[Neogrendelismic chords]] || [[Neogrendelismic]] || [[5985/5984]] | |||
|- | |||
| [[Heartland #Chords|Heartland chords]] || [[Heartland]] || 243/242, 1083/1078 | |||
|} | |||
=== 23-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Scanismic chords]] || [[Scanismic]] || [[460/459]] | |||
|- | |||
| [[Pittsburghismic chords]] || [[Pittsburghismic]] || [[484/483]] | |||
|- | |||
| [[Laodicismic chords]] || [[Laodicismic]] || [[507/506]] | |||
|- | |||
| [[Preziosismic chords]] || [[Preziosismic]] || [[529/528]] | |||
|- | |||
| [[Worcester chords]] || [[Worcester]] || [[576/575]] | |||
|- | |||
| [[Harvardismic chords]] || [[Harvardismic]] || [[736/735]] | |||
|- | |||
| [[Squadronismic chords]] || [[Squadronismic]] || [[760/759]] | |||
|- | |||
| [[Lysistratismic chords]] || [[Lysistratismic]] || [[897/896]] | |||
|- | |||
| [[Fragarismic chords]] || [[Fragarismic]] || [[1105/1104]] | |||
|- | |||
| [[Rodessismic chords]] || [[Rodessismic]] || [[1197/1196]] | |||
|- | |||
| [[Triaphonismic chords]] || [[Triaphonismic]] || [[1288/1287]] | |||
|- | |||
| [[Turkismic chords]] || [[Turkismic]] || [[1496/1495]] | |||
|- | |||
| [[Antinousismic chords]] || [[Antinousismic]] || [[1863/1862]] | |||
|- | |||
| [[Artifismic chords]] || [[Artifismic]] || [[2024/2023]] | |||
|- | |||
| [[Cupcake chords]] || [[Cupcake]] || [[2025/2024]] | |||
|- | |||
| [[Guangdongismic chords]] || [[Guangdongismic]] || [[2185/2184]] | |||
|- | |||
| [[Travellismic chords]] || [[Travellismic]] || [[2300/2299]] | |||
|- | |||
| [[Biyativice chords]] || [[Biyativice]] || [[2646/2645]] | |||
|- | |||
| [[Kotkismic chords]] || [[Kotkismic]] || [[2737/2736]] | |||
|- | |||
| [[Vicious chords]] || [[Vicious]] || [[3060/3059]] | |||
|- | |||
| [[Mikkolismic chords]] || [[Mikkolismic]] || [[3381/3380]] | |||
|- | |||
| [[Vicedim chords]] || [[Vicedim]] || [[3520/3519]] | |||
|- | |||
| [[Shoalmic chords]] || [[Shoalmic]] || [[3888/3887]] | |||
|- | |||
| [[Viceaug chords]] || [[Viceaug]] || [[4693/4692]] | |||
|- | |||
| [[Demiquartervice chords]] || [[Demiquartervice]] || [[4761/4760]] | |||
|- | |||
| [[Broadviewsmic chords]] || [[Broadviewsmic]] || [[5083/5082]] | |||
|- | |||
| [[Vicetertismic chords]] || [[Vicetertismic]] || [[Vicetertisma|12168/12167]] | |||
|} | |||
=== 25-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Tunbarsmic chords]] || [[Tunbarsmic]] || [[625/624]] | |||
|- | |||
| [[Nymphismic chords]] || [[Nymphismic]] || [[875/874]] | |||
|- | |||
| [[Noellismic chords]] || [[Noellismic]] || [[1225/1224]] | |||
|- | |||
| [[Trichthonismic chords]] || [[Trichthonismic]] || [[2376/2375]] | |||
|- | |||
| [[Sperasmic chords]] || [[Sperasmic]] || [[2500/2499]] | |||
|- | |||
| [[Lehmerismic chords]] || [[Lehmerismic temperaments|Lehmerismic]] || [[3025/3024]] | |||
|- | |||
| [[Martebismic chords]] || [[Martebismic]] || [[3250/3249]] | |||
|- | |||
| [[Leprechaun chords]] || [[Leprechaun]] || [[4225/4224]] | |||
|- | |||
| [[Neovishmic chords]] || [[Neovishmic]] || [[5776/5775]] | |||
|- | |||
| [[Neonewtismic chords]] || [[Neonewtismic]] || [[6175/6174]] | |||
|} | |||
=== 27-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Ragismic chords]] || [[Ragismic microtemperaments|Ragismic]] || [[4375/4374]] | |||
|- | |||
| [[Hagendorfismic chords]] || [[Hagendorfismic]] || [[8075/8073]] | |||
|} | |||
=== 29-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Vinecute chords]] || [[Vinecute]] || [[4641/4640]] | |||
|- | |||
| [[Large grapevine chords]] || [[Large grapevine]] || [[4901/4900]] | |||
|- | |||
| [[Small grapevine chords]] || [[Small grapevine]] || [[7425/7424]] | |||
|- | |||
| [[Vinous chords]] || [[Vinous]] || [[8671/8670]] | |||
|} | |||
=== 31-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Kibismic chords]] || [[Kibismic]] || [[1024/1023]] | |||
|- | |||
| [[Acronymismic chords]] || [[Acronymismic]] || [[Acronymisma|17577/17576]] | |||
|- | |||
| [[Tricecubismic chords]] || [[Tricecubismic]] || [[Tricecubisma|29792/29791]] | |||
|} | |||
=== 33-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Wizardharry chords]] || [[Wizardharry]] || [[4000/3993]] | |||
|- | |||
| [[Flashmic chords]] || [[The Flashmob|Flashmic]] || [[12376/12375]] | |||
|} | |||
=== 35-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Lummic chords]] || [[Lummic]] || [[1716/1715]] | |||
|} | |||
=== 37-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Bullionismic chords]] || [[Bullionismic]] || [[5292/5291]] | |||
|} | |||
=== 39-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Harmonismic chords]] || [[Harmonismic]] || [[10648/10647]] | |||
|} | |||
=== 55-odd-limit === | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Jacobin chords]] || [[The Jacobins|Jacobin]] || [[6656/6655]] | |||
|} | |||
== List of innate comma chords == | |||
{| class="wikitable" | |||
|- | |||
! Chords !! Associated Temperament !! Associated Commas | |||
|- | |||
| [[Diminished seventh chord]] || [[Diminished (temperament)|Diminished]] || [[36/35]], [[50/49]] | |||
|- | |||
| [[Augmented triad]] || [[Augmented (temperament)|Augmented]] || [[128/125]] | |||
|} | |||
== List of essentially just dyadic chords == | |||
As chords that are unambiguous counterparts to common JI chords are not of particular relevance to this page, most of the entries here will be what [[User:Kaiveran|Kaiveran]] calls '''plurichords''', where there are multiple sets of consonances that a given chord can be mapped to. Note that this can still lead to ambiguous tonality in the case of otonal and utonal intervals being identified together. | |||
{| class="wikitable" | |||
|+ | |||
! Chords | |||
! Equivalent Mappings | |||
! Associated Commas | |||
|- | |||
| [[Hendrix chord]] | |||
| <font style="font-size:0.85em">8:10:14:19 ~ 12:15:21:28</font> | |||
| [[57/56]] | |||
|- | |||
| [[Rootsubminor triad]] | |||
| 6:7:9 ~ 16:19:24 | |||
| 57/56 | |||
|- | |||
| [[The Biosphere|Biosphere]] triads | |||
| 6:7:9 ~ 26:30:39 <br>10:13:15 ~ 14:18:21 | |||
| [[91/90]] | |||
|- | |||
| [[Rootminor triad]] | |||
| 10:12:15 ~ 16:19:24 | |||
| [[96/95]] | |||
|- | |||
| [[Lynchismic chords|Lynchismic plurichords]] | |||
| <font style="font-size:0.85em">12:14:17:20 ~ 1/(20:17:14:12) <br>6:7:8:10 ~ 1/(20:17:15:12)</font> | |||
| [[120/119]] | |||
|- | |||
| [[Augustmic chords|Augustmic plurichords]] | |||
| <font style="font-size:0.85em">14:17:18:22 ~ 1/(22:18:17:14)</font> | |||
| [[154/153]] | |||
|} | |||
== See also == | |||
* [[Essential tempering comma]] | |||
== Notes == | |||
[[Category:Terms]] | |||
[[Category:Regular temperament theory]] | |||
[[Category:Dyadic chords| ]] <!-- main article --> | |||
[[Category:Lists of chords]] | |||
<references /> | |||
Latest revision as of 11:21, 4 August 2025
- Not to be confused with Dyad.
A dyadic chord, also described as a dyadically consonant chord or pairwise consonant chord, is a chord each of whose intervals belongs to a specified set of intervals considered to be consonant; it is therefore relative to the set of intervals in question.
For example, the tetrad
- 1 – 6/5 – 7/5 – 8/5
is a dyadic chord in the 7-odd-limit since every interval involved in it is an element of the 7-odd-limit tonality diamond. Now if we replace 7/5 with 10/7:
- 1 – 6/5 – 10/7 – 8/5
is not a dyadic chord in the 7-odd-limit. Although each note is 7-odd-limit over the bass, the interval between 10/7 and 6/5 is 25/21, and that between 10/7 and 8/5 is 28/25 – these are not 7-odd-limit.
The significance of dyadic chords and of the paradigm where all interval pairs are examined in the chord has the psychoacoustic basis of timbral fusion and emergence of the virtual fundamental. In the above examples, it can be shown that the lower harmonics of each note in the first chord blends better than in the second. Meanwhile, the virtual fundamental of the first chord appears 5/1 below the bass, whereas that of the second appears much lower, at 35/1 below the bass as the denominators "fight" each other. For these reasons we tend to find the first chord more consonant than the second.
Essentially tempered dyadic chord
In regular temperament theory, we may speak of a just or tempered dyadic chord. By a just dyadic chord is meant a chord in just intonation which is dyadic, so that each of its notes in relation to the lowest note is a rational number belonging to the set of consonances, and moreover each interval between the notes belongs to the set of consonances. An essentially just dyadic chord is a chord which is considered to be an approximation of a just dyadic chord, such that each of its intervals is considered to be an approximation of the corresponding interval in the just dyadic chord. So, for instance, 1 – 5/4 – 3/2 is a just dyadic chord when the consonance set is the 5-odd-limit diamond with octave equivalence, and 0 – 10 – 18 in 31edo with consonance set {8, 10, 13, 18, 21, 23, 31} modulo 31 is an essentially just dyadic chord approximating 1 – 5/4 – 3/2.
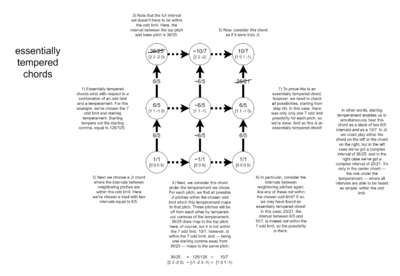
An essentially tempered dyadic chord is a chord defined in a regular temperament and relative to a set of consonances such that each interval is within that consonance set, but there is no corresponding just dyadic chord. This means there is no just chord such that each interval, when mapped by the abstract regular temperament, belongs to the consonance set. For example, the chord 1 – 6/5 – 10/7, when mapped by starling temperament, which makes 126/125 vanish, has each of its intervals in the set of 7-odd-limit consonances which is the tempering of the 7-odd-limit diamond by 126/125 (this is because 10/7 is off from 36/25 by 126/125, and therefore 10/7 and 36/25 are tempered together in starling temperament, and since 36/25 = (6/5)², the interval from 6/5 to 10/7 in starling may be heard as a second move by 6/5). However, (10/7)/(6/5) = 25/21 is 25-odd-limit, and there is no other 7-odd-limit just dyadic chord which can be used instead to give the result, so it is an essentially tempered dyadic chord.
Essentially tempered dyadic chords are a related notion to comma pumps, and can be used as a basis for creating pumps. Using essentially tempered chords in chord progressions breaks the harmony out of exclusively just chord relations, and serves as a sort of harmonic lubricant imparting fluidity and dynamism to the harmony, at the cost fairly often of some blurring of the sense of tonality.
Innate comma chord
An innate comma chord, proposed by Kite Giedraitis, is the type of chord that cannot be mapped to just intonation in a given prime limit and odd limit. However, instead of specifying the targeted JI ratios as in an essentially tempered chord, an innate comma chord describes only the general chord shape: the mapped interval representations or the sizes of its constituent intervals. For example, the augmented triad in 5-limit JI is an innate comma chord below the 25-odd-limit, because it is impossible to tune all three major thirds (in the four-note chord doubling the root up an octave) to 5/4 or any other 5-limit interval with odd limit below 25: the innate comma here is 128/125 (41¢). In practice, it might be sung or played justly but with a large odd limit (containing wolf intervals): for example, 1–5/4–8/5–2, or 1–5/4–25/16–2 (or even 1–5/4–25/16–125/64). Or it might be tempered, e.g. in 12edo as 0¢–400¢–800¢–1200¢. In 7-limit JI, one of the major thirds can be tuned to 9/7, reducing the innate comma to 225/224 (only 8¢). This comma can be distributed among the three thirds, tempering each by only a few cents, which is usually close enough to be acceptable. In 11-limit JI, the augmented chord is not an innate comma chord, because it can be tuned justly as 7:9:11:14, a low enough odd limit to "ring". (However, it is debatable whether this chord qualifies as an augmented triad, because the middle 11/9 interval is a neutral third rather than a major third.)
Anomalous saturated suspension
An anomalous saturated suspension (ASS), introduced by Graham Breed[1], is a q-odd-limit just dyadic chord to which no pitch q-odd-limit pitch class can be added while keeping it in the q-odd-limit, and which is neither an otonal or a utonal chord; that is, it is not contained as a subchord of either the 1:3:5:…:q chord or the 1:1/3:1/5:…:1/q chord. The existence of such chords was discovered by Paul Erlich[2]. Below are listed two 9-odd-limit ASSes of special interest, as they avoid intervals smaller than a minor whole tone.
For a complete list of ASS chords through the 23-odd-limit see List of anomalous saturated suspensions.
List of just intonation tetrads
- Seven limit tetrads
- Nine limit tetrads
- 1-3-7-11 tetrads
- Thirteen limit tetrads
- Fifteen limit tetrads
- Seventeen limit tetrads
List of essentially tempered dyadic chords
Here are some pages on certain essentially tempered dyadic chords, sorted by the lowest odd limit in which they are available. See Dyadic chord/Pattern of essentially tempered chords for some notable abstract chord patterns.
7-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Archytas chords | Archytas | 64/63 |
| Starling chords | Starling | 126/125 |
9-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Didymic chords | Meantone | 81/80 |
| Marvel chords | Marvel | 225/224 |
| Sensamagic chords | Sensamagic | 245/243 |
11-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Mothwellsmic chords | Mothwellsmic | 99/98 |
| Ptolemismic chords | Ptolemismic | 100/99 |
| Biyatismic chords | Biyatismic | 121/120 |
| Valinorsmic chords | Valinorsmic | 176/175 |
| Rastmic chords | Rastmic | 243/242 |
| Frostmic chords | Frostmic | 245/242 |
| Keenanismic chords | Keenanismic | 385/384 |
| Werckismic chords | Werckismic | 441/440 |
| Swetismic chords | Swetismic | 540/539 |
| Pentacircle chords | Pentacircle | 896/891 |
| Undecimal marvel chords | Marvel | 225/224, 385/384 |
| Prodigy chords | Prodigy | 225/224, 441/440 |
| Undecimal sensamagic chords | Sensamagic | 245/243, 385/384 |
| Jove chords | Jove | 243/242, 441/440 |
| Miracle chords | Miracle | 225/224, 243/242, 385/384 |
| Magic chords | Magic | 100/99, 225/224, 245/243 |
| Supermagic chords | Supermagic | 100/99, 385/384 |
| Orwell tetrad | Guanyin | 176/175, 540/539 |
| Tutonic hexads | Meantone | 81/80, 99/98, 126/125 |
| Baldanders hexads | Andromeda | 100/99, 225/224, 245/242 |
| Porcupine heptad | Porkypine | 55/54, 100/99 |
13-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Buzurgismic chords | Buzurgismic | 169/168 |
| Mynucumic chords | Mynucumic | 196/195 |
| Gassormic chords | Gassormic | 275/273 |
| Marveltwin chords | Marveltwin | 325/324 |
| Ratwolfsmic chords | Ratwolfsmic | 351/350 |
| Major minthmic chords | Major minthmic | 352/351 |
| Minor minthmic chords | Minor minthmic | 364/363 |
| Huntmic chords | Huntmic | 640/637 |
| Squbemic chords | Squbemic | 729/728 |
| Cuthbert chords | Cuthbert | 847/845 |
| Sinbadmic chords | Sinbadmic | 1001/1000 |
| Kestrel chords | Kestrel | 1188/1183 |
| Catadictmic chords | Catadictmic | 1287/1280 |
| Lambeth chords | Lambeth | 1573/1568 |
| Petrmic chords | Petrmic | 2200/2197 |
| Rastgross heptad | Namo | 144/143, 243/242 |
| Parapyth chords | Parapyth, gentle | 352/351, 364/363 |
| Hecate hexad | Hecate | 225/224, 325/324, 385/384 |
| Woodpecker octad | Woodpecker | 66/65, 121/120, 126/125 |
| Miraculous decad | Miraculous, Revelation | 105/104, 196/195, 512/507 |
15-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Island chords | Island | 676/675 |
| Nicolic chords | Nicolic | 1575/1573 |
| Myhemiwell chords | Myhemiwell | 3388/3375 |
| Battaglia chord | Marvel | 225/224 |
| Tetracot chords | Tetracot | 100/99, 243/242 |
| Orwell ennead | Guanyin | 176/175, 540/539 |
17-odd-limit
19-odd-limit
21-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Slendric pentad | Gamelismic | 1029/1024 |
| Palingenetic chords | Palingenetic | 1701/1700 |
| Xenismic chords | Xenismic | 2058/2057 |
| Ibnsinmic chords | Ibnsinmic | 2080/2079 |
| Heartlandismic chords | Heartlandismic | 3971/3969 |
| Schisminic chords | Schisminic | 4096/4095 |
| Baladismic chords | Baladismic | 4914/4913 |
| Neogrendelismic chords | Neogrendelismic | 5985/5984 |
| Heartland chords | Heartland | 243/242, 1083/1078 |
23-odd-limit
25-odd-limit
27-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Ragismic chords | Ragismic | 4375/4374 |
| Hagendorfismic chords | Hagendorfismic | 8075/8073 |
29-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Vinecute chords | Vinecute | 4641/4640 |
| Large grapevine chords | Large grapevine | 4901/4900 |
| Small grapevine chords | Small grapevine | 7425/7424 |
| Vinous chords | Vinous | 8671/8670 |
31-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Kibismic chords | Kibismic | 1024/1023 |
| Acronymismic chords | Acronymismic | 17577/17576 |
| Tricecubismic chords | Tricecubismic | 29792/29791 |
33-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Wizardharry chords | Wizardharry | 4000/3993 |
| Flashmic chords | Flashmic | 12376/12375 |
35-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Lummic chords | Lummic | 1716/1715 |
37-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Bullionismic chords | Bullionismic | 5292/5291 |
39-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Harmonismic chords | Harmonismic | 10648/10647 |
55-odd-limit
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Jacobin chords | Jacobin | 6656/6655 |
List of innate comma chords
| Chords | Associated Temperament | Associated Commas |
|---|---|---|
| Diminished seventh chord | Diminished | 36/35, 50/49 |
| Augmented triad | Augmented | 128/125 |
List of essentially just dyadic chords
As chords that are unambiguous counterparts to common JI chords are not of particular relevance to this page, most of the entries here will be what Kaiveran calls plurichords, where there are multiple sets of consonances that a given chord can be mapped to. Note that this can still lead to ambiguous tonality in the case of otonal and utonal intervals being identified together.
| Chords | Equivalent Mappings | Associated Commas |
|---|---|---|
| Hendrix chord | 8:10:14:19 ~ 12:15:21:28 | 57/56 |
| Rootsubminor triad | 6:7:9 ~ 16:19:24 | 57/56 |
| Biosphere triads | 6:7:9 ~ 26:30:39 10:13:15 ~ 14:18:21 |
91/90 |
| Rootminor triad | 10:12:15 ~ 16:19:24 | 96/95 |
| Lynchismic plurichords | 12:14:17:20 ~ 1/(20:17:14:12) 6:7:8:10 ~ 1/(20:17:15:12) |
120/119 |
| Augustmic plurichords | 14:17:18:22 ~ 1/(22:18:17:14) | 154/153 |