Porcupine
| Porcupine |
55/54, 100/99 (2.3.5.11);
55/54, 64/63, 100/99 (2.3.5.7.11)
((11-limit) 15-odd limit) 19.9 ¢
((11-limit) 15-odd limit) 37 notes
Porcupine is a temperament that is generated by a minor whole tone which is tuned flat to around 160–165 cents, and the porcupine comma (250/243) is tempered out. Two generators (stacked) represent 6/5, and three represent 4/3; from this, the generator itself represents a (severely flattened) 10/9. This is obviously in stark contrast to meantone temperaments, including 12edo, where 10/9 is tuned sharp and equated with 9/8 so that two of them reach a major third of 5/4. The "equal tetrachord" formed by dividing 4/3 into 3 equal parts is a characteristic feature of many of porcupine's scales.
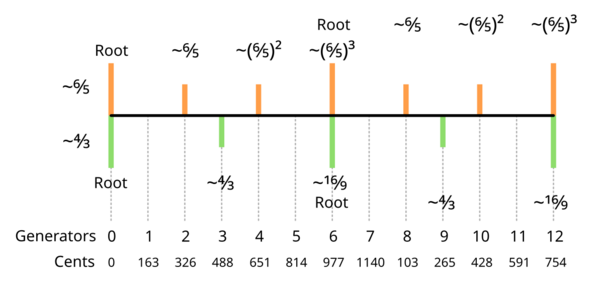
One may also note that in just intonation, a stack of three 6/5's is flat of the classical minor seventh 9/5 by 25/24, and a stack of two 4/3's is the Pythagorean minor seventh 16/9, which is flat of 9/5 by 81/80. Thus, it can be determined that porcupine equates the syntonic comma 81/80 with the 5-limit chromatic semitone 25/24, which simplifies the 5-limit to a rank-2 structure in a simple way distinct from temperaments that reduce it to a strong extension of pythagorean (such as meantone and schismic).
Porcupine can be thought of as a 2.3.5.11-subgroup temperament (sometimes called porkypine) without much additional damage compared to the 5-limit; the generator here represents not only 10/9, but also 11/10 and 12/11 (equivalently, 55/54, 100/99, and 121/120 are tempered out), with the consequence that the 11/9 interval, usually considered a neutral third, is in porcupine identical to the 6/5 minor third, due to the extreme flatness of 10/9. This also means that 27/20, the 5-limit "acute fourth", is equivalent to 11/8 (rather than becoming 4/3 as in meantone), found at −4 generators (tuned to about 540–560 cents). This is because as the syntonic comma has been expanded, sharpening a fourth by a comma now leads to a significantly sharp interval close to the 11th harmonic. Porcupine is one of the most efficient temperaments in the 2.3.5.11 subgroup at a certain standard of accuracy.
It is also very easy to extend porcupine to prime 7, because the 16/9, found at +6 generators (tuned to about 960–990 cents), has already been flattened to merge it with (6/5)3, and therefore can be equated to 7/4. This makes porcupine a weak extension of archy, splitting its generator into three parts; its Pythagorean major third is mapped to 9/7, and its fifth is tuned sharp, ranging from around 705–720 cents, with the best tunings around 711–712 cents, which roughly splits the damage on 7/4 and 9/7.
See Porcupine family #Porcupine for technical data and alternative 7-limit extensions. See Porcupine extensions for a discussion on 13-limit extensions.
Interval chain
In the following table, odd harmonics 1–11 are in bold.
| Up from the tonic, and fourthward | Down from the octave, and fifthward | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| # | Cents* | Ratios | Porcupine notation |
Ups and downs notation |
# | Cents* | Ratios | Porcupine notation |
Ups and downs notation |
| 0 | 0.0 | 1/1 | P1 | P1 | 0 | 1200.0 | 2/1 | P8 | P8 |
| 1 | 162.8 | 10/9, 11/10, 12/11 | P2 | vM2 = ^^m2 | −1 | 1037.2 | 9/5, 11/6, 20/11 | P7 | ^m7 = vvM7 |
| 2 | 325.6 | 6/5, 11/9 | m3 | ^m3 = vvM3 | −2 | 874.4 | 5/3, 18/11 | M6 | vM6 = ^^m6 |
| 3 | 488.4 | 4/3 | m4 | P4 | −3 | 711.6 | 3/2 | M5 | P5 |
| 4 | 651.3 | 16/11, 22/15 | m5 | v5 = ^^d5 | −4 | 548.7 | 11/8, 15/11 | M4 | ^4 = vvA4 |
| 5 | 814.1 | 8/5 | m6 | ^m6 = vvM6 | −5 | 385.9 | 5/4 | M3 | vM3 = ^^m3 |
| 6 | 976.9 | 7/4, 16/9 | d7 | m7 | −6 | 223.1 | 8/7, 9/8 | A2 | M2 |
| 7 | 1139.7 | 35/18, 48/25, 64/33 | d8 | v8 = ^^d8 | −7 | 60.3 | 25/24, 33/32, 36/35 | A1 | ^1 = vvA1 |
| 8 | 102.5 | 16/15, 21/20 | d2 | ^m2 = vvM2 | −8 | 1097.5 | 15/8, 40/21 | A7 | vM7 = ^^m7 |
| 9 | 265.3 | 7/6 | d3 | m3 | −9 | 934.7 | 12/7 | A6 | M6 |
| 10 | 428.2 | 14/11 | d4 | v4 = ^^d4 | −10 | 771.8 | 11/7 | A5 | ^5 = vvA5 |
| 11 | 591.0 | 7/5 | d5 | ^d5 = vv5 | −11 | 609.0 | 10/7 | A4 | vA4 = ^^4 |
| 12 | 753.8 | 14/9 | d6 | m6 | −12 | 446.2 | 9/7 | A3 | M3 |
* In 11-limit CWE tuning, octave reduced
In the ups and downs notation, the enharmonic unison is the trudsharp, the triple-down augmented unison. The porcupine notation does not have an enharmonic unison.
Besides the specific tuning shown here, there is a range of acceptable porcupine tunings that includes generators as small as 160 cents (15edo) and as large as 165.5 cents (29edo). However, the 29edo patent val does not support 11-limit porcupine proper, since it does not temper out 64/63.
Chords and harmony
12/11, 11/10, and 10/9 are all represented by the same interval, the generator. This makes chords such as 8:9:10:11:12 exceptionally common and easy to find.
| 8:9:10:11:12 chord, in just intonation. All intervals are slightly different. |
Porcupine-tempered 8:9:10:11:12 chord, in 22edo. Except the first, the intervals are the same. |
Porcupine-tempered 8:9:10:11:12 chord, in 29edo. Except the first, the intervals are the same. |
The interval representing both 25/24 and 81/80 can be found in this interval chain at −7 steps, and ranges from about 45 to 80 ¢ depending on the tuning. This can be considered the "chroma" of porcupine temperament.
Scales
- Mos scales, tuning optimized on the 2.3.5.11 subgroup
- Mos scales, 8/5.12/7 eigenmonzo (unchanged interval) tuning
Tunings
| Euclidean | |||
|---|---|---|---|
| Constrained | Constrained & skewed | Destretched | |
| Equilateral | CEE: ~10/9 = 163.6049 ¢ | CSEE: ~10/9 = 163.2835 ¢ | POEE: ~10/9 = 163.9280 ¢ |
| Tenney | CTE: ~10/9 = 164.1659 ¢ | CWE: ~10/9 = 164.0621 ¢ | POTE: ~10/9 = 163.9504 ¢ |
| Benedetti, Wilson |
CBE: ~10/9 = 164.3761 ¢ | CSBE: ~10/9 = 164.3761 ¢ | POBE: ~10/9 = 164.1610 ¢ |
| Euclidean | |||
|---|---|---|---|
| Constrained | Constrained & skewed | Destretched | |
| Equilateral | CEE: ~11/10 = 163.1459 ¢ | CSEE: ~11/10 = 162.8445 ¢ | POEE: ~11/10 = 164.1867 ¢ |
| Tenney | CTE: ~11/10 = 163.8867 ¢ | CWE: ~11/10 = 163.9951 ¢ | POTE: ~11/10 = 164.0777 ¢ |
| Benedetti, Wilson |
CBE: ~11/10 = 164.2393 ¢ | CSBE: ~11/10 = 164.4623 ¢ | POBE: ~11/10 = 164.2221 ¢ |
| Euclidean | |||
|---|---|---|---|
| Constrained | Constrained & skewed | Destretched | |
| Equilateral | CEE: ~11/10 = 162.4448 ¢ | CSEE: ~11/10 = 162.2333 ¢ | POEE: ~11/10 = 162.2522 ¢ |
| Tenney | CTE: ~11/10 = 163.1055 ¢ | CWE: ~11/10 = 162.8156 ¢ | POTE: ~11/10 = 162.7474 ¢ |
| Benedetti, Wilson |
CBE: ~11/10 = 163.5299 ¢ | CSBE: ~11/10 = 163.2310 ¢ | POBE: ~11/10 = 163.0304 ¢ |
Tuning spectrum
| EDO generator |
Unchanged interval (eigenmonzo)* |
Generator (¢) | Comments |
|---|---|---|---|
| 1\8 | 150.000 | Lower bound of 5-odd-limit diamond monotone | |
| 12/11 | 150.637 | Lower bound of 11- and 15-odd-limit diamond tradeoff | |
| 6/5 | 157.821 | 1/2-comma; lower bound of 5-, 7-, and 9-odd-limit diamond tradeoff | |
| 2\15 | 160.000 | Lower bound of 7- to (11-limit) 15-odd-limit diamond monotone | |
| 7/4 | 161.471 | ||
| 7\52 | 161.538 | 52b val | |
| 14/11 | 161.751 | ||
| 7/5 | 162.047 | ||
| 5\37 | 162.162 | ||
| 16/11 | 162.171 | ||
| 8\59 | 162.712 | ||
| 8/5 | 162.737 | 2/5-comma, 5-odd and 7-odd minimax | |
| 28/15 | 162.897 | ||
| 7/6 | 162.986 | ||
| 3\22 | 163.636 | Upper bound of 7- to (11-limit) 15-odd-limit diamond monotone | |
| 14/9 | 163.743 | 9-, 11-, and (11-limit) 15-odd-limit minimax | |
| 16/15 | 163.966 | 3/8-comma | |
| 7\51 | 164.706 | 51d val | |
| 11/10 | 165.004 | ||
| 4\29 | 165.517 | 29d val | |
| 22/15 | 165.762 | ||
| 4/3 | 166.015 | 1/3-comma; upper bound of 5- and 7-odd-limit diamond tradeoff | |
| 5\36 | 166.667 | 36cde val | |
| 1\7 | 171.429 | Upper bound of 5-odd-limit diamond monotone | |
| 11/9 | 173.704 | ||
| 10/9 | 182.404 | Untempered generator; upper bound of 9- to 15-odd-limit diamond tradeoff |
* besides the octave
History
Porcupine temperament/scales were discovered by Dave Keenan, but did not have a name until Herman Miller mentioned that his Mizarian Porcupine Overture in 15et had a section that pumps the 250/243 comma. Although this music did not use a porcupine mos or modmos (which would have 7 or 8 notes), the name was adopted for such scales as well, once the essentially one-to-one relationship between vanishing commas and sequences of DE scales was fully evident. It was clear that even though Herman's piece was in 15edo, 22edo was a porcupine tuning par excellence, and that was an interesting development in itself.
See also
Music
20th century
- Mizarian Porcupine Overture (1999) – play – in 15edo tuning, namesake of the temperament
21st century
- "April Porkfest" from TOTMC Suite Vol. 1 (2023) – in 11-limit CTE tuning
- Porcupine Walk (2019)
- Sanctus (2015)
- being a (2010) – in Porcupine[8], mode 1|6, 22edo tuning
- Porcupeen (2017)
- "Porcupine", from pato, with friends (2019)
- Second Breakfast (15edo) (2018)[dead link]
- Porcupine Experience (2012) – in 22edo tuning
- Flying Straight Down (2020) – in 22edo tuning
- Life on Mars (2014)
- Porcupine Lullaby (2020) – in 37edo tuning
- Porcupine[7] Modal Fugues – 7-piece playlist
- Night on Porcupine Mountain (archived 2010) – in 22edo tuning
- Gently Playing With Miller's Porcupine (2011) – blog | play – in Porcupine[7], mode 3|3, 15edo tuning
- 15 Porcupines in India – sarangi, tambura and sitar improvisation
- 15 Quills – piano solo
- Prickly Side of Love – rock band with vocals
- Porcupine Organ Composition
- Porcupine Prelude 1 – in 22edo tuning
- Porcupine Prelude 2 – in 22edo tuning
- Porcupine Prelude 3 – in 22edo tuning
- Porcupine Praeambulum – in 22edo tuning
- Porcupine Chorale with Prelude "Nature's Lament" – in 22edo tuning
- Porcupine Major Overture (2015) – in 22edo tuning
- Waltzing in Candyland (2015) – in Porcupine[8], 15edo tuning