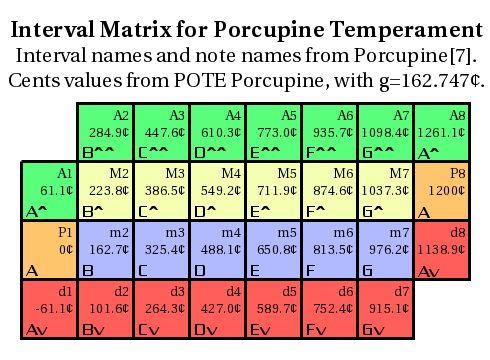
Porcupine intervals
These are the intervals found in porcupine temperament.
In 22edo, all the neighboring intervals on this chart that are shown as about 20 cents apart are actually the same. For example, the augmented third (9/7) and the diminished fourth (14/11) are both the same interval (8\22) in 22edo. This corresponds to 99/98 being tempered out in 22edo.
In 15edo, on the other hand, the intervals that are shown as about 40 cents apart are actually the same. For example, the augmented third (9/7), is now the same as a minor fourth (4/3) rather than a diminished one. That is because 28/27 is tempered out in 15edo.
| Name (ups and downs) | Name (1L 6s (onyx)) | Size* | Ratio | Genspan | Comments |
|---|---|---|---|---|---|
| Unisons | |||||
| Perfect unison (P1) | Perfect unison (P1) | 0.0 | 1/1 | 0 | |
| Up unison (^1) | Augmented unison (A1) | 61.1 | 81/80~36/35~33/32~25/24 | -7 | Among other ratios |
| Seconds | |||||
| Upminor second (^m2) | Diminished second (d2) | 101.6 | 21/20~16/15 | 8 | |
| Downmajor second (vM2) | Perfect second (P2) | 162.7 | 12/11~11/10~10/9~35/32 | 1 | |
| Major second (M2) | Augmented second (A2) | 223.8 | 9/8~8/7 | -6 | |
| Upmajor second (^M2) | Double-augmented second (AA2) | 284.9 | Close to 13/11 | -13 | Also "subminor third" |
| Thirds | |||||
| Minor third (m3) | Diminished third (d3) | 264.3 | 7/6 | 9 | Also "supermajor second" |
| Upminor third (^m3) | Minor third (m3) | 325.4 | 6/5~11/9 | 2 | |
| Downmajor third (vM3) | Major third (M3) | 386.5 | 5/4 | -5 | |
| Major third (M3) | Augmented third (A3) | 447.6 | 9/7 (close to 13/10) | -12 | Also "subminor fourth" |
| Fourths | |||||
| Down fourth (v4) | Diminished fourth (d4) | 427.0 | 14/11 | 10 | Also "supermajor third" |
| Perfect fourth (P4) | Minor fourth (m4) | 488.1 | 4/3 | 3 | |
| Upfourth (^4) | Major fourth (M4) | 549.2 | 11/8 | -4 | |
| Downaugmented fourth (vA4) | Augmented fourth (A4) | 610.3 | 10/7 | -11 | Also "subminor fifth" |
| Fifths | |||||
| Updiminished fifth (^d5) | Diminished fifth (d5) | 589.7 | 7/5 | 11 | Also "supermajor fourth" |
| Down fifth (v5) | Minor fifth (m5) | 650.8 | 16/11 | 4 | |
| Perfect fifth (P5) | Major fifth (M5) | 711.9 | 3/2 | -3 | |
| Up fifth (^5) | Augmented fifth (A5) | 773.0 | 11/7 | -10 | Also "subminor sixth" |
| Sixths | |||||
| Minor sixth (m6) | Diminished sixth (d6) | 752.4 | 14/9 (close to 20/13) | 12 | Also "supermajor fifth" |
| Upminor sixth (^m6) | Minor sixth (m6) | 813.5 | 8/5 | 5 | |
| Downmajor sixth (vM6) | Major sixth (M6) | 874.6 | 5/3 | -2 | |
| Major sixth (M6) | Augmented sixth (A6) | 935.7 | 12/7 | -9 | Also "subminor seventh" |
| Sevenths | |||||
| Downminor seventh (vm7) | Double-diminished seventh (dd7) | 915.1 | Close to 22/13 | 13 | Also "supermajor sixth" |
| Minor seventh (m7) | Diminished seventh (d7) | 976.2 | 7/4~16/9 | 6 | |
| Upminor seventh (^m7) | Perfect seventh (P7) | 1037.3 | 9/5~11/6 | -1 | |
| Downmajor seventh (vM7) | Augmented seventh (A7) | 1098.4 | 15/8 | -8 | |
| Octaves | |||||
| Down octave (v8) | Diminished octave (d8) | 1138.9 | 21/11~35/18~160/81 | 7 | |
| Perfect octave (P8) | Perfect octave (P8) | 1200.0 | 2/1 | 0 | |
| Up octave (^8) | Augmented octave (A8) | 1261.1 | 81/40~45/22~33/16~25/12 | -7 | |
- In cents, 11-limit POTE tuning of porcupine, where the generator is ~162.7¢.