19edo
| ← 18edo | 19edo | 20edo → |
19 equal divisions of the octave (abbreviated 19edo or 19ed2), also called 19-tone equal temperament (19tet) or 19 equal temperament (19et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 19 equal parts of about 63.2 ¢ each. Each step represents a frequency ratio of 21/19, or the 19th root of 2.
History
Interest in this tuning system goes back to the sixteenth century, when composer Guillaume Costeley used it in his chanson Seigneur Dieu ta pitié of 1558. Costeley understood and desired the circulating aspect of this tuning, which he defined as dividing the just major second into three approximately equal parts. Costeley had other compositions that made use of intervals, such as the diminished third, which have a meaningful context in 19edo, but not in other tuning systems contemporary with the work.
In 1577 music theorist Francisco de Salinas proposed 1⁄3-comma meantone, in which the fifth is 694.786 ¢; the fifth of 19edo is 694.737 ¢, which is only a twentieth of a cent flatter. Salinas suggested tuning nineteen tones to the octave to this tuning, which comes within less than one cent of closing exactly, so that his suggestion is effectively 19edo.
In 1835, mathematician and music theorist Wesley Woolhouse proposed it as a more practical alternative to meantone tunings he regarded as better, such as 50 equal temperament (summary of Woolhouse's essay).
Theory
Having an almost just minor third and perfect fifths and major thirds about 7 cents flat, 19edo serves as a good tuning for meantone. Unlike 12edo, where enharmonic notes are conflated, 19edo distinguishes them, and differs from 17edo in that its diatonic semitone is wider than the chromatic semitone, rather than narrower. In fact, it is nearly identical to the enharmonic scale of 1/3-comma meantone, and can be considered a closed form thereof.
As an approximation of other temperaments
Besides meantone, 19edo is also suitable for magic/muggles temperament, because five of its major thirds are equivalent to one of its twelfths. Its 7-step supermajor third can be used for sensi, whose generator is a very sharp major third, two of which make an approximate 5/3 major sixth.
For all of these there are more optimal tunings: the fifth of 19edo is flatter than the usual for meantone, and 31edo is more optimal. Similarly, the generating interval of magic temperament is a major third, and again 19edo's is flatter; 41edo more closely matches it. It does make for a good tuning for muggles, but in 19edo it is the same as magic. Finally, 19edo can be used as a tuning for sensi, though 46edo provides a better sensi tuning.
However, for all of these 19edo has the practical advantage of requiring fewer pitches, which makes it easier to implement in physical instruments, and many 19edo instruments have been built. 19edo is in fact the second edo, after 12edo which is able to approximate 5-limit intervals and chords with tolerable accuracy (unless you count 15edo, which has a 18-cent-sharp fifth). It is less successful in the 7-limit (but still better than 12edo), as it conflates the septimal subminor third (7/6) with the septimal whole tone (8/7). 19edo also has the advantage of being excellent for negri, keemun, godzilla, muggles, and triton/liese. Keemun and negri are of particular note for being very simple 7-limit temperaments, with their mos scales in 19edo offering a great abundance of septimal tetrads. The Graham complexity of a 7-limit tetrad is 6 for keemun, 7 for negri, 8 for godzilla, 10 for meantone, 11 for triton, 12 for magic/muggles, and 13 for sensi.
As a means of extending harmony
Because 19edo's 5-limit chords are more blended and concordant than those of 12edo, it can be a much better candidate for using alternate forms of harmony such as quartal, secundal, and poly chords. William Lynch suggests the use of seventh chords of various types to be the fundamental sonorities with a triad deemed as incomplete. Higher extensions involving the 7th harmonic as well as other non-diatonic chord extensions which tend to clash in 12edo blend much better in 19edo.
In addition, Joseph Yasser talks about the idea of a 12-tone supra-diatonic scale where the 7-tone major scale in 19edo becomes akin to the pentatonic of western music; as it would sound to a future generation, ambiguous and not tonally fortified. As paraphrased "A system in which the undeniable laws of tonal gravity exist, yet in a much more complex tonal universe." Yasser believed that music would eventually move to a 19-tone system with a 12-note supra-diatonic scale would become the standard. While this has yet to happen, Yasser's concept of supra-diatonicity is intriguing and worth exploring for those wanting to extend tonality without sounding too alien.
19edo also closely approximates most of the intervals of Bozuji tuning, a 21st century tuning based on Gioseffo Zarlino's approach to just intonation. with most of the adjacent diatonic diminished and augmented intervals of Bozuji tuning represented enharmonically by one interval in 19edo.
Due to the narrow whole tones and wide diatonic semitones, 19edo's diatonic scale tends to sound somewhat dull compared to 12edo, but the pentatonic scale is said by many to sound much more expressive owing to the significantly larger contrast between the narrow whole tone and wide minor third. While 12edo has an expressive diatonic and dull pentatonic, the reverse is true in 19. Pentatonicism thus becomes more important in 19edo, and one option is to use the pentatonic scale as a sort of "super-chord", with "chord progressions" being modulations between pentatonic subsets of the superdiatonic scale.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -7.2 | -7.4 | -21.5 | +17.1 | -19.5 | +21.4 | +18.3 | +3.3 | -19.1 | -8.2 | +1.3 |
| Relative (%) | +0.0 | -11.4 | -11.7 | -34.0 | +27.1 | -30.8 | +33.8 | +28.9 | +5.2 | -30.2 | -13.0 | +2.0 | |
| Steps (reduced) |
19 (0) |
30 (11) |
44 (6) |
53 (15) |
66 (9) |
70 (13) |
78 (2) |
81 (5) |
86 (10) |
92 (16) |
94 (18) |
99 (4) | |
Adaptive tuning
The no-11's 13-limit is represented relatively well and consistently. 19edo's negri, sensi and godzilla scales have many 13-limit chords. (You can think of the Sensi[8] 3L 5s mos scale as 19edo's answer to the diminished scale. Both are made of two diminished seventh chords, but Sensi[8] gives you additional ratios of 7 and 13.) Its diminished fifth is also a very accurate approximation of the 23rd harmonic, being only 3.3 ¢ off 23/16.
Practically 19edo can be used adaptively on instruments which allow you to bend notes up: by different amounts, the 3rd, 5th, 7th, and 13th harmonics are all tuned flat. This is in contrast to 12edo, where this is not possible since the 5th and 7th harmonics are not only much farther from just than they are in 19edo, but fairly sharp already.
Another option would be to use octave stretching, which has similar benefits to adaptive use, but it also works for fixed-pitch Instruments. For more on that see the section: 19edo#Octave stretch.
Subsets and supersets
19edo is the 8th prime edo, following 17edo and preceding 23edo. As such, it does not contain any nontrivial subset edos, though it contains 19ed4.
38edo, which doubles 19edo, provides an approximation of harmonic 11 that works well with the flat tendency of its 5-limit mapping. See undevigintone. 57edo effectively corrects the harmonic 7 to just, although it is 76edo that fits the best. See meanmag.
Intervals
| Degree | Cents | Interval Region | Approximated JI Intervals[note 1] | Solfege | SKULO Interval | |
|---|---|---|---|---|---|---|
| 0 | 0.00 | Unison (prime) | 1/1 | Do | unison | P1 |
| 1 | 63.16 | Augmented unison | 25/24, 26/25, 28/27 | Di/Ro | super unison, subminor second | S1, sm2 |
| 2 | 126.32 | Minor second | 13/12, 14/13, 15/14, 16/15 | Ra | minor second | m2 |
| 3 | 189.47 | Major second | 9/8, 10/9 | Re | major second | M2 |
| 4 | 252.63 | Augmented second Diminished third |
7/6, 8/7, 15/13 | Ri/Ma | supermajor second, subminor third | SM2, sm3 |
| 5 | 315.79 | Minor third | 6/5 | Me | minor third | m3 |
| 6 | 378.95 | Major third | 5/4, 16/13, 56/45 | Mi | major third | M3 |
| 7 | 442.11 | Augmented third | 9/7, 13/10, 32/25 | Mo/Fe | supermajor third, sub fourth | SM3, s4 |
| 8 | 505.26 | Perfect fourth | 4/3, 75/56 | Fa | perfect fourth | P4 |
| 9 | 568.42 | Augmented fourth (Small tritone) |
7/5, 18/13, 25/18 | Fi | augmented fourth | A4 |
| 10 | 631.58 | Diminished fifth (Large tritone) |
10/7, 13/9, 36/25 | Se | diminished fifth | d5 |
| 11 | 694.74 | Perfect fifth | 3/2, 112/75 | So | perfect fifth | P5 |
| 12 | 757.89 | Augmented fifth | 14/9, 20/13, 25/16 | Si/Lo | super fifth, subminor sixth | S5, sm6 |
| 13 | 821.05 | Minor sixth | 8/5, 13/8, 45/28 | Le | minor sixth | m6 |
| 14 | 884.21 | Major sixth | 5/3 | La | major sixth | M6 |
| 15 | 947.37 | Augmented sixth Diminished seventh |
7/4, 12/7, 26/15 | Li/Ta | supermajor sixth, subminor seventh | SM6, sm7 |
| 16 | 1010.53 | Minor seventh | 9/5, 16/9 | Te | minor seventh | m7 |
| 17 | 1073.68 | Major seventh | 13/7, 15/8, 24/13, 28/15 | Ti | major seventh | M7 |
| 18 | 1136.84 | Augmented seventh | 25/13, 27/14, 48/25 | To/Da | supermajor seventh, sub octave | SM7, s8 |
| 19 | 1200.00 | Octave | 2/1 | Do | octave | P8 |
Interval quality and chord names in color notation
Using color notation, qualities can be loosely associated with colors:
| Quality | Color Name | Monzo Format | Examples |
|---|---|---|---|
| diminished | zo | (a, b, 0, 1) | 7/6, 7/4 |
| minor | fourthward wa | (a, b), b < −1 | 32/27, 16/9 |
| gu | (a, b, −1) | 6/5, 9/5 | |
| major | yo | (a, b, 1) | 5/4, 5/3 |
| fifthward wa | (a, b), b > 1 | 9/8, 27/16 | |
| augmented | ru | (a, b, 0, −1) | 9/7, 12/7 |
Key signatures are the same, but with the extra notes and different enharmonic equivalents, some key signatures can get messy. For example, the key of B𝄫 would have double-flats on B and E, and flats on C, D, F, G, and A. Thinking of rewriting this key as A♯ might seem better, but then the key signature would contain double-sharps on C, F, and G, and sharps on A, B, D, and E, which is actually worse.
All 19edo chords can be named using conventional methods, expanded to include augmented and diminished 2nd, 3rds, 6ths and 7ths. Here are the zo, gu, yo and ru triads:
| Color of the 3rd | JI Chord | Edosteps | Notes of C Chord | Written Name | Spoken Name |
|---|---|---|---|---|---|
| zo (7-over) | 6:7:9 | 0–4–11 | C–E𝄫–G | Cm(♭3) or Cmin(♭3) or C(d3) | C subminor, C minor flat-three, C dim-three |
| gu (5-under) | 10:12:15 | 0–5–11 | C–E♭–G | Cm or Cmin | C minor |
| yo (5-over) | 4:5:6 | 0–6–11 | C–E–G | C or Cmaj | C, C major |
| ru (7-under) | 14:18:21 | 0–7–11 | C–E♯–G | C(♯3) or Cmaj(♯3) or C(A3) | C supermajor, C major sharp-three, C aug-three |
| yo (5-over) | 4:5:6:7 | 0–6–11–15 | C–E–G–B𝄫 | Ch7 or C,d7 or Cadd(d7) | C harmonic 7, C (major) add dim-seven |
| gu (5-under) | 12:10:8:7 or 1:6/5:3/2:12/7 | 0–5–11–15 | C–E♭–G–A♯ | Cm♯6 or CmA6 or Cm(add(♯6)) or Cm(add(A6)) | C minor (add) sharp-six, C minor (add) aug-six |
The last two chords illustrate how the 15\19 interval can be considered as either 7/4 or 12/7, and how 19edo conflates zo and ru ratios.
For a more complete list, see 19edo Chord Names and Ups and downs notation #Chords and Chord Progressions.
Notation
Standard notation
Standard 12edo notation can be used, whether it is staff notation (with five lines), letter chain-of-fifths notation (with standard accidentals), solfege, or sargam. Note that D# and Eb are two different notes.
Any 19edo note or interval can be respelled enharmonically by adding a double-diminished 2nd to it or subtracting one from it. Adding a dd2 is equivalent to finding the 12edo equivalent with a higher degree, then diminishing it. For example, C# becomes Db, which is diminished to become Dbb.
| Degree | Cents | Standard Notation | |
|---|---|---|---|
| Diatonic Interval Names | Note Names on D | ||
| 0 | 0.00 | Perfect unison (P1) | D |
| 1 | 63.16 | Augmented unison (A1) Diminished second (d2) |
D# Ebb |
| 2 | 126.32 | Doubly augmented unison (AA1) Minor second (m2) |
Dx Eb |
| 3 | 189.47 | Major second (M2) Doubly diminished third (dd3) |
E Fbb |
| 4 | 252.63 | Augmented second (A2) Diminished third (d3) |
E# Fb |
| 5 | 315.79 | Doubly augmented second (AA2) Minor third (m3) |
Ex F |
| 6 | 378.95 | Major third (M3) Doubly diminished fourth (dd4) |
F# Gbb |
| 7 | 442.11 | Augmented third (A3) Diminished fourth (d4) |
Fx Gb |
| 8 | 505.26 | Perfect fourth (P4) | G |
| 9 | 568.42 | Augmented fourth (A4) Doubly diminished fifth (dd5) |
G# Abb |
| 10 | 631.58 | Doubly augmented fourth (AA4) Diminished fifth (d5) |
Gx Ab |
| 11 | 694.74 | Perfect fifth (P5) | A |
| 12 | 757.89 | Augmented fifth (A5) Diminished sixth (d6) |
A# Bbb |
| 13 | 821.05 | Doubly augmented fifth (AA5) Minor sixth (m6) |
Ax Bb |
| 14 | 884.21 | Major sixth (M6) Doubly diminished seventh (dd7) |
B Cbb |
| 15 | 947.37 | Augmented sixth (A6) Diminished seventh (d7) |
B# Cb |
| 16 | 1010.53 | Doubly augmented sixth (AA6) Minor seventh (m7) |
Bx C |
| 17 | 1073.68 | Major seventh (M7) Doubly diminished octave (dd8) |
C# Dbb |
| 18 | 1136.84 | Augmented seventh (A7) Diminished octave (d8) |
Cx Db |
| 19 | 1200.00 | Perfect octave (P8) | D |
In 19edo:
- Ups and downs notation is identical to standard notation;
- Mixed sagittal notation is identical to standard notation, but pure sagittal notation exchanges sharps (♯) and flats (♭) for sagittal sharp (
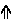 ) and sagittal flat (
) and sagittal flat ( ) respectively.
) respectively.
| Step offset | −2 | −1 | 0 | +1 | +2 |
|---|---|---|---|---|---|
| Symbol | |
|
|
|
|
Sagittal notation
This notation uses the same sagittal sequence as EDOs 5, 12, and 26, and is a subset of the notations for EDOs 38, 57, and 76.
Evo flavor
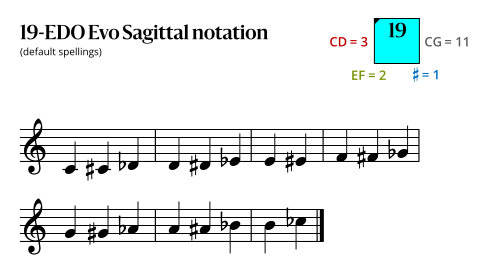
Because it includes no Sagittal symbols, this Evo Sagittal notation is also a conventional notation.
Revo flavor
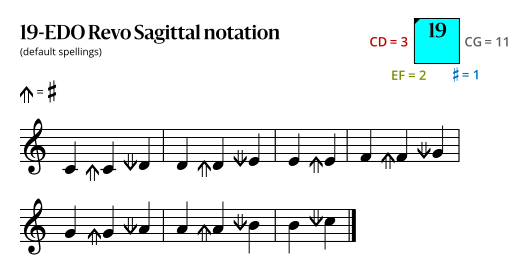
Dodecatonic notation
| Degree | Cents | Interval Names |
|---|---|---|
| 0 | 0.00 | P1 |
| 1 | 63.16 | A1, m2 |
| 2 | 126.32 | M2, m3 |
| 3 | 189.47 | M3 |
| 4 | 252.63 | m4, A3 |
| 5 | 315.79 | M4, m5 |
| 6 | 378.95 | M5 |
| 7 | 442.11 | A5, d6 |
| 8 | 505.26 | P6 |
| 9 | 568.42 | A6, m7 |
| 10 | 631.58 | M7, d8 |
| 11 | 694.74 | P8 |
| 12 | 757.89 | A8, m9 |
| 13 | 821.05 | M9, m10 |
| 14 | 884.21 | M10 |
| 15 | 947.37 | m11, A10 |
| 16 | 1010.53 | M11, m12 |
| 17 | 1073.68 | M12 |
| 18 | 1136.84 | A12, d13 |
| 19 | 1200.00 | P13 |
Approximation to JI

Interval mappings
The following tables show how 15-odd-limit intervals are represented in 19edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 5/3, 6/5 | 0.148 | 0.2 |
| 13/7, 14/13 | 1.982 | 3.1 |
| 15/13, 26/15 | 4.891 | 7.7 |
| 13/9, 18/13 | 5.039 | 8.0 |
| 15/14, 28/15 | 6.873 | 10.9 |
| 9/7, 14/9 | 7.021 | 11.1 |
| 9/5, 10/9 | 7.070 | 11.2 |
| 3/2, 4/3 | 7.218 | 11.4 |
| 5/4, 8/5 | 7.366 | 11.7 |
| 13/10, 20/13 | 12.109 | 19.2 |
| 13/12, 24/13 | 12.257 | 19.4 |
| 7/5, 10/7 | 14.091 | 22.3 |
| 7/6, 12/7 | 14.239 | 22.5 |
| 9/8, 16/9 | 14.436 | 22.9 |
| 15/8, 16/15 | 14.585 | 23.1 |
| 11/8, 16/11 | 17.103 | 27.1 |
| 13/8, 16/13 | 19.475 | 30.8 |
| 7/4, 8/7 | 21.457 | 34.0 |
| 11/6, 12/11 | 24.321 | 38.5 |
| 11/10, 20/11 | 24.469 | 38.7 |
| 11/7, 14/11 | 24.597 | 38.9 |
| 13/11, 22/13 | 26.580 | 42.1 |
| 15/11, 22/15 | 31.470 | 49.8 |
| 11/9, 18/11 | 31.539 | 49.9 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 5/3, 6/5 | 0.148 | 0.2 |
| 13/7, 14/13 | 1.982 | 3.1 |
| 15/13, 26/15 | 4.891 | 7.7 |
| 13/9, 18/13 | 5.039 | 8.0 |
| 15/14, 28/15 | 6.873 | 10.9 |
| 9/7, 14/9 | 7.021 | 11.1 |
| 9/5, 10/9 | 7.070 | 11.2 |
| 3/2, 4/3 | 7.218 | 11.4 |
| 5/4, 8/5 | 7.366 | 11.7 |
| 13/10, 20/13 | 12.109 | 19.2 |
| 13/12, 24/13 | 12.257 | 19.4 |
| 7/5, 10/7 | 14.091 | 22.3 |
| 7/6, 12/7 | 14.239 | 22.5 |
| 9/8, 16/9 | 14.436 | 22.9 |
| 15/8, 16/15 | 14.585 | 23.1 |
| 11/8, 16/11 | 17.103 | 27.1 |
| 13/8, 16/13 | 19.475 | 30.8 |
| 7/4, 8/7 | 21.457 | 34.0 |
| 11/6, 12/11 | 24.321 | 38.5 |
| 11/10, 20/11 | 24.469 | 38.7 |
| 11/9, 18/11 | 31.539 | 49.9 |
| 15/11, 22/15 | 31.688 | 50.2 |
| 13/11, 22/13 | 36.578 | 57.9 |
| 11/7, 14/11 | 38.561 | 61.1 |
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [-30 19⟩ | [⟨19 30]] | +2.277 | 2.277 | 3.612 |
| 2.3.5 | 81/80, 3125/3072 | [⟨19 30 44]] | +2.578 | 1.911 | 3.025 |
| 2.3.5.7 | 49/48, 81/80, 126/125 | [⟨19 30 44 53]] | +3.848 | 2.755 | 4.362 |
| 2.3.5.7.13 | 49/48, 65/64, 81/80, 91/90 | [⟨19 30 44 53 70]] | +4.135 | 2.530 | 4.006 |
| 2.3.5.7.13.23 | 49/48, 65/64, 70/69, 81/80, 91/90 | [⟨19 30 44 53 70 86]] | +3.319 | 2.936 | 4.649 |
- 19et is lower in relative error than any previous equal temperaments in the 5-, 7-, 13-, 17-, and 19-limit—both 19 and 19e val achieve this in the case of 13-limit, 19eg val in the 17-limit, and 19egh val in the 19-limit. The next equal temperaments doing better in those subgroups are 34, 31, 27e, 22, and 26, respectively.
- 19et is best in the 2.3.5.7.13 subgroup, and the next equal temperament that does better in this is 53.
Uniform maps
| Min. size | Max. size | Wart notation | Map |
|---|---|---|---|
| 18.7816 | 18.9337 | 19e | ⟨19 30 44 53 65 70] |
| 18.9337 | 19.0518 | 19 | ⟨19 30 44 53 66 70] |
| 19.0518 | 19.0571 | 19f | ⟨19 30 44 53 66 71] |
| 19.0571 | 19.1651 | 19df | ⟨19 30 44 54 66 71] |
| 19.1651 | 19.2228 | 19cdf | ⟨19 30 45 54 66 71] |
Commas
19et tempers out the following commas. (Note: This assumes the val ⟨19 30 44 53 66 70].)
| Prime limit |
Ratio[note 2] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | (20 digits) | [-30 19⟩ | 137.14 | Trilawa | 19-comma |
| 5 | 16875/16384 | [-14 3 4⟩ | 51.12 | Laquadyo | Negri comma |
| 5 | (14 digits) | [-2 13 -8⟩ | 34.91 | Laquadbigu | Unicorn comma |
| 5 | 3125/3072 | [-10 -1 5⟩ | 29.61 | Laquinyo | Magic comma |
| 5 | 81/80 | [-4 4 -1⟩ | 21.51 | Gu | Syntonic comma |
| 5 | 78732/78125 | [2 9 -7⟩ | 13.40 | Sepgu | Sensipent comma |
| 5 | 15625/15552 | [-6 -5 6⟩ | 8.11 | Tribiyo | Kleisma |
| 5 | (20 digits) | [8 14 -13⟩ | 5.29 | Thegu | Parakleisma |
| 5 | (28 digits) | [-14 -19 19⟩ | 2.82 | Neyo | Enneadeca |
| 7 | 59049/57344 | [-13 10 0 -1⟩ | 50.72 | Laru | Harrison's comma |
| 7 | 1029/1000 | [-3 1 -3 3⟩ | 49.49 | Trizogu | Keega |
| 7 | 525/512 | [-9 1 2 1⟩ | 43.41 | Lazoyoyo | Avicennma |
| 7 | 49/48 | [-4 -1 0 2⟩ | 35.70 | Zozo | Semaphoresma, slendro diesis |
| 7 | 3645/3584 | [-9 6 1 -1⟩ | 29.22 | Laruyo | Schismean comma |
| 7 | 686/675 | [1 -3 -2 3⟩ | 27.99 | Trizo-agugu | Senga |
| 7 | 875/864 | [-5 -3 3 1⟩ | 21.90 | Zotrigu | Keema |
| 7 | 245/243 | [0 -5 1 2⟩ | 14.19 | Zozoyo | Sensamagic comma |
| 7 | 126/125 | [1 2 -3 1⟩ | 13.79 | Zotrigu | Starling comma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Ruyoyo | Marvel comma |
| 7 | 19683/19600 | [-4 9 -2 -2⟩ | 7.32 | Labirugu | Cataharry comma |
| 7 | 10976/10935 | [5 -7 -1 3⟩ | 6.48 | Satrizo-agu | Hemimage comma |
| 7 | 3136/3125 | [6 0 -5 2⟩ | 6.08 | Zozoquingu | Hemimean comma |
| 7 | (12 digits) | [-11 2 7 -3⟩ | 1.63 | Latriru-asepyo | Metric comma |
| 7 | 4375/4374 | [-1 -7 4 1⟩ | 0.40 | Zoquadyo | Ragisma |
| 11 | 45/44 | [-2 2 1 0 -1⟩ | 38.91 | Luyo | Undecimal fifth tone |
| 11 | 56/55 | [3 0 -1 1 -1⟩ | 31.19 | Luzogu | Undecimal tritonic comma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 896/891 | [7 -4 0 1 -1⟩ | 9.69 | Saluzo | Pentacircle comma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.39 | Satrilu-aruru | Orgonisma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.21 | Lururuyo | Swetisma |
| 13 | 39/38 | [-1 1 0 0 0 1 0 -1⟩ | 44.97 | Nutho | Undevicesimal two-ninth tone |
| 13 | 65/64 | [-6 0 1 0 0 1⟩ | 26.84 | Thoyo | Wilsorma |
| 13 | 343/338 | [-1 0 0 3 0 -2⟩ | 25.42 | Thuthutrizo | |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap comma, biome comma |
| 13 | 676/675 | [2 -3 -2 0 0 2⟩ | 2.56 | Bithogu | Island comma |
| 13 | 1001/1000 | [-3 0 -3 1 1 1⟩ | 1.73 | Tholozotrigu | Fairytale comma, sinbadma |
| 23 | 2187/2116 | [-2 7 0 0 0 0 0 0 -2⟩ | 57.14 | Labitwethu | Lipsett comma |
| 23 | 70/69 | [1 -1 1 1 0 0 0 0 -⟩ | 24.91 | Twethuzoyo | Small vicesimotertial eighth tone |
| 23 | 256/253 | [8 0 0 0 -1 0 0 0 -1⟩ | 20.41 | Twethulu | 253rd subharmonic |
| 23 | 161/160 | [-5 0 -1 1 0 0 0 0 1⟩ | 10.79 | Twethozogu | Major kirnbergisma |
| 23 | 208/207 | [4 -2 0 0 0 1 0 0 -1⟩ | 8.34 | Twethutho | Vicetone comma |
| 23 | 529/528 | [-4 -1 0 0 -1 0 0 0 2⟩ | 3.28 | Bitwetho-alu | Preziosisma |
| 23 | 576/575 | [6 2 -2 0 0 0 0 0 -1⟩ | 3.01 | Twethugugu | Worcester comma |
| 23 | 1288/1287 | [3 -2 0 1 -1 -1 0 0 1⟩ | 1.34 | Twethothuluzo | Triaphonisma |
Linear temperaments
- List of 19et rank two temperaments by badness
- List of 19et rank two temperaments by complexity
- List of edo-distinct 19et rank two temperaments
- Syntonic–kleismic equivalence continuum
Since 19 is prime, all rank-2 temperaments in 19edo have one period per octave (i.e. are linear). Therefore you can make a correspondence between intervals and the linear temperaments they generate.
| Degree | Cents | Interval | Mos scales | Temperaments |
|---|---|---|---|---|
| 1 | 63.16 | A1, d2 | Unicorn / Rhinoceros | |
| 2 | 126.32 | m2 | 1L 8s, 9L 1s | Negri |
| 3 | 189.47 | M2 | 1L 5s, 6L 1s, 6L 7s | Deutone Spell |
| 4 | 252.63 | A2, d3 | 1L 3s, 4L 1s, 5L 4s, 5L 9s |
Godzilla |
| 5 | 315.79 | m3 | 3L 1s, 4L 3s, 4L 7s, 4L 11s |
Cata / keemun |
| 6 | 378.95 | M3 | 3L 1s, 3L 4s, 3L 7s, 3L 10s, 3L 13s |
Magic / muggles |
| 7 | 442.11 | A3, d4 | 3L 2s, 3L 5s, 8L 3s | Sensi |
| 8 | 505.26 | P4 | 2L 3s, 5L 2s, 7L 5s | Meantone / flattone |
| 9 | 568.42 | A4 | 2L 3s, 2L 5s, 2L 7s, 2L 9s, 2L 11s, 2L 13s, 2L 15s |
Liese / pycnic Triton |
Octave stretch or compression
Pianos are frequently tuned with stretched octaves anyway due to the slight inharmonicity inherent in their strings, which makes 19edo a promising option for pianos with split sharps.
Octave stretching also means that an out-of-tune interval can be replaced with a compounded or inverted version of it which is near-just. For example, if we are using 49ed6 or 30edt (which tune 6:1 and 3:1 just and have octaves stretched by 2.8 and 4.57 ¢, respectively), then we have near-just minor thirds (6:5), compound major thirds (as 5:1), and compound fifths (as 6:1), giving us versions of everything in the 5-odd-limit tonality diamond. The compound major and minor triads (1:5:6 and 30:6:5) are near-just as well.
What follows is a comparison of stretched-octave 19edo tunings.
- 19edo
- Step size: 63.158 ¢, octave size: 1200.000 ¢
Pure-octaves 19edo approximates all harmonics up to 16 within 21.5 ¢.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | -7.2 | +0.0 | -7.4 | -7.2 | -21.5 | +0.0 | -14.4 | -7.4 | +17.1 | -7.2 |
| Relative (%) | +0.0 | -11.4 | +0.0 | -11.7 | -11.4 | -34.0 | +0.0 | -22.9 | -11.7 | +27.1 | -11.4 | |
| Steps (reduced) |
19 (0) |
30 (11) |
38 (0) |
44 (6) |
49 (11) |
53 (15) |
57 (0) |
60 (3) |
63 (6) |
66 (9) |
68 (11) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -19.5 | -21.5 | -14.6 | +0.0 | +21.4 | -14.4 | +18.3 | -7.4 | -28.7 | +17.1 | +3.3 | -7.2 |
| Relative (%) | -30.8 | -34.0 | -23.1 | +0.0 | +33.8 | -22.9 | +28.9 | -11.7 | -45.4 | +27.1 | +5.2 | -11.4 | |
| Steps (reduced) |
70 (13) |
72 (15) |
74 (17) |
76 (0) |
78 (2) |
79 (3) |
81 (5) |
82 (6) |
83 (7) |
85 (9) |
86 (10) |
87 (11) | |
- Step size: 63.293 ¢, octave size: 1202.569 ¢
Stretching the octave of 19edo by about 2.6 ¢ results in just noticeably improved primes 3, 5, 7 and 13, but a just noticeably worse prime 11. This approximates all harmonics up to 16 but 11 within 14.3 ¢. Both 5-limit TE and WE tuning do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +2.6 | -3.2 | +5.1 | -1.4 | -0.6 | -14.3 | +7.7 | -6.3 | +1.2 | +26.0 | +2.0 |
| Relative (%) | +4.1 | -5.0 | +8.1 | -2.2 | -0.9 | -22.6 | +12.2 | -10.0 | +1.8 | +41.1 | +3.1 | |
| Step | 19 | 30 | 38 | 44 | 49 | 53 | 57 | 60 | 63 | 66 | 68 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -10.0 | -11.7 | -4.6 | +10.3 | -31.4 | -3.8 | +29.2 | +3.7 | -17.5 | +28.6 | +14.9 | +4.5 |
| Relative (%) | -15.8 | -18.5 | -7.2 | +16.2 | -49.6 | -5.9 | +46.2 | +5.9 | -27.6 | +45.2 | +23.6 | +7.2 | |
| Step | 70 | 72 | 74 | 76 | 77 | 79 | 81 | 82 | 83 | 85 | 86 | 87 | |
- Step size: 63.305 ¢, octave size: 1202.799 ¢
Stretching the octave of 19edo by about 2.8 ¢ results in greatly improved primes 3, 5, 7 and 13, but a greatly worse prime 11. This approximates all harmonics up to 16 but 11 within 13.7 ¢. The tuning 49ed6 does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +2.8 | -2.8 | +5.6 | -0.9 | +0.0 | -13.7 | +8.4 | -5.6 | +1.9 | +26.8 | +2.8 |
| Relative (%) | +4.4 | -4.4 | +8.8 | -1.4 | +0.0 | -21.6 | +13.3 | -8.8 | +3.0 | +42.4 | +4.4 | |
| Steps (reduced) |
19 (19) |
30 (30) |
38 (38) |
44 (44) |
49 (0) |
53 (4) |
57 (8) |
60 (11) |
63 (14) |
66 (17) |
68 (19) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -9.2 | -10.9 | -3.7 | +11.2 | -30.5 | -2.8 | +30.2 | +4.7 | -16.4 | +29.6 | +16.0 | +5.6 |
| Relative (%) | -14.5 | -17.1 | -5.8 | +17.7 | -48.1 | -4.4 | +47.7 | +7.4 | -26.0 | +46.8 | +25.2 | +8.8 | |
| Steps (reduced) |
70 (21) |
72 (23) |
74 (25) |
76 (27) |
77 (28) |
79 (30) |
81 (32) |
82 (33) |
83 (34) |
85 (36) |
86 (37) |
87 (38) | |
- Step size: 63.331 ¢, octave size: 1203.288 ¢
Stretching the octave of 19edo by around 3.5 ¢ results in greatly improved primes 3, 5, 7 and 13, but a greatly worse prime 11. This approximates all harmonics up to 16 but 11 within 13.2 ¢. The tuning 65zpi does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.3 | -2.0 | +6.6 | +0.2 | +1.3 | -12.3 | +9.9 | -4.1 | +3.5 | +28.5 | +4.5 |
| Relative (%) | +5.2 | -3.2 | +10.4 | +0.4 | +2.0 | -19.4 | +15.6 | -6.4 | +5.6 | +45.0 | +7.2 | |
| Step | 19 | 30 | 38 | 44 | 49 | 53 | 57 | 60 | 63 | 66 | 68 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -7.4 | -9.0 | -1.8 | +13.2 | -28.5 | -0.8 | -31.0 | +6.8 | -14.3 | -31.5 | +18.2 | +7.8 |
| Relative (%) | -11.6 | -14.2 | -2.8 | +20.8 | -45.0 | -1.2 | -49.0 | +10.8 | -22.6 | -49.8 | +28.7 | +12.4 | |
| Step | 70 | 72 | 74 | 76 | 77 | 79 | 80 | 82 | 83 | 84 | 86 | 87 | |
- Step size: 63.374 ¢, octave size: 1204.109 ¢
Stretching the octave of 19edo by around 4.1 ¢ results in greatly improved primes 3, 5, 7 and 13, but a greatly worse prime 11. This approximates all harmonics up to 16 but 11 within 16.4 ¢. Both 2.3.5.7.13-subgroup TE and WE tuning do this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +4.1 | -0.7 | +8.2 | +2.1 | +3.4 | -10.0 | +12.3 | -1.5 | +6.3 | +31.4 | +7.5 |
| Relative (%) | +6.5 | -1.2 | +13.0 | +3.4 | +5.3 | -15.8 | +19.4 | -2.3 | +9.9 | +49.5 | +11.8 | |
| Step | 19 | 30 | 38 | 44 | 49 | 53 | 57 | 60 | 63 | 66 | 68 | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -4.3 | -5.9 | +1.4 | +16.4 | -25.1 | +2.6 | -27.6 | +10.4 | -10.7 | -27.9 | +21.9 | +11.6 |
| Relative (%) | -6.8 | -9.3 | +2.2 | +25.9 | -39.7 | +4.2 | -43.5 | +16.4 | -16.9 | -44.0 | +34.6 | +18.3 | |
| Step | 70 | 72 | 74 | 76 | 77 | 79 | 80 | 82 | 83 | 84 | 86 | 87 | |
- Step size: 63.399 ¢, octave size: 1204.572 ¢
Stretching the octave of 19edo by around 4.5 ¢ has similar results to 65zpi, but it overshoots the optimum, meaning the improvements are less and the drawbacks are greater compared to 65zpi. The damage to the octave has also started to become noticeable when it is stretched this far. This approximates all harmonics up to 16 but 11 within 18.3 ¢. The tuning 30edt does this.
| Harmonic | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +4.6 | +0.0 | +9.1 | +3.2 | +4.6 | -8.7 | +13.7 | +0.0 | +7.8 | -30.4 | +9.1 |
| Relative (%) | +7.2 | +0.0 | +14.4 | +5.1 | +7.2 | -13.7 | +21.6 | +0.0 | +12.3 | -48.0 | +14.4 | |
| Steps (reduced) |
19 (19) |
30 (0) |
38 (8) |
44 (14) |
49 (19) |
53 (23) |
57 (27) |
60 (0) |
63 (3) |
65 (5) |
68 (8) | |
| Harmonic | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.6 | -4.1 | +3.2 | +18.3 | -23.3 | +4.6 | -25.6 | +12.4 | -8.7 | -25.8 | +24.0 | +13.7 |
| Relative (%) | -4.2 | -6.5 | +5.1 | +28.8 | -36.7 | +7.2 | -40.4 | +19.5 | -13.7 | -40.8 | +37.9 | +21.6 | |
| Steps (reduced) |
70 (10) |
72 (12) |
74 (14) |
76 (16) |
77 (17) |
79 (19) |
80 (20) |
82 (22) |
83 (23) |
84 (24) |
86 (26) |
87 (27) | |
One can stretch the octave even further – 12.5 cents – to get the tuning 11edf, but its approximations of most harmonics are worse than pure-octaves 19. So it is hard to see a use case for 11edf.
Scales
MOS scales
Octave-equivalent mosses
- meantone pentatonic, 2L 3s (gen = 11\19): 3 3 5 3 5
- meantone diatonic, 5L 2s (gen = 11\19): 3 3 2 3 3 3 2
- meantone chromatic, 7L 5s (gen = 11\19): 2 1 2 1 2 2 1 2 1 2 1 2
- semaphore[5], 4L 1s (gen = 4\19): 4 4 3 4 4
- semaphore[9], 5L 4s (gen = 4\19): 3 1 3 1 3 3 1 3 1
- semaphore[14], 5L 9s (gen = 4\19): 2 1 2 1 1 2 1 1 2 1 1 2 1 1
- sensi[5], 2L 3s (gen = 7\19): 5 2 5 2 5
- sensi[8], 3L 5s (gen = 7\19): 2 3 2 2 3 2 2 3
- sensi[11], 8L 3s (gen = 7\19): 2 2 1 2 2 2 1 2 2 2 1
- negri[9], 1L 8s (gen = 2\19): 2 2 2 2 3 2 2 2 2
- negri[10], 9L 1s (gen = 2\19): 2 2 2 2 2 1 2 2 2 2
- kleismic[7], 4L 3s (gen = 5\19): 1 4 1 4 1 4 4
- kleismic[11], 4L 7s (gen = 5\19): 1 3 1 1 3 1 1 3 1 3 1
- kleismic[15], 4L 11s (gen = 5\19): 1 2 1 1 1 2 1 1 1 2 1 1 2 1 1
- magic[7], 3L 4s (gen = 6\19): 5 1 5 1 5 1 1
- magic[10], 3L 7s (gen = 6\19): 4 1 1 4 1 1 4 1 1 1
- magic[13], 3L 10s (gen = 6\19): 3 1 1 1 3 1 1 1 3 1 1 1 1
- magic[16], 3L 13s (gen = 6\19): 2 1 1 1 1 2 1 1 1 1 2 1 1 1 1 1
- liese[17], 2L 15s (gen = 9\19): 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1
Other scales
- Meantone harmonic minor: 3 2 3 3 2 4 2
- Meantone melodic minor: 3 2 3 3 3 3 2
- Meantone harmonic major: 3 3 2 3 2 4 2
- chromatic octave species - Meantone / marvel double harmonic major (subset of Negri[9]): 2 4 2 3 2 4 2
- chromatic octave species (subset of Negri[9]): 2 2 4 3 2 2 4
- chromatic octave species - Sahara septatonic (subset of Negri[9]): 4 2 2 3 4 2 2
- Marvel hexatonic (subset of Negri[9]): 4 2 5 2 4 2
- enharmonic pentatonic: 2 6 3 2 6
- enharmonic pentatonic: 6 2 3 6 2
- enharmonic octave species: 1 1 6 3 1 1 6
- enharmonic octave species: 6 1 1 3 6 1 1
- enharmonic octave species: 1 6 1 3 1 6 1
- Pinetone major-harmonic octatonic: 3 2 3 1 2 3 2 3 (subset of Meantone[12])
- Pinetone minor-harmonic octatonic: 3 2 1 3 2 3 3 2 (subset of Meantone[12])
- Pinetone diminished octatonic / Porcusmine: 2 3 1 3 2 3 2 3
- Pinetone harmonic diminished: 2 3 1 4 1 3 2 3
- Blackville / 5-limit dipentatonic (superset of Meantone[7]): 1 2 3 2 1 2 3 2 1 2
- Antipental blues: 4 4 1 2 4 4
- Semiquartal 3|5 b2: 1 3 3 1 3 1 3 3 1
- 5-odd-limit tonality diamond: 5 1 2 3 2 1 5
- 7-odd-limit tonality diamond: 4 1 1 2 1 1 1 2 1 1 4
- 9-odd-limit tonality diamond: 3 1 1 1 1 1 1 1 1 1 1 1 1 1 3
Instruments


Music
- See also: Category:19edo tracks
- XA 19-ET Index
- A number of compositions that were perfomed at the midwestmicrofest concert in 2007[dead link]
See also
- 19edo modes
- 19edo chords
- Strictly proper 19edo scales
- How to tune a 19edo guitar by ear
- Primer for 19edo
- Mason Green's New Common Practice Notation
- Extraclassical tonality
- Lumatone mapping for 19edo
Further reading
- Darreg, Ivor. A Case for Nineteen. 1982.
- Darreg, Ivor. Nineteen for the Nineties[dead link]. (Unknown date of publication).
- Howe, Hubert S., Jr. 19-Tone Theory and Applications. c. 2004.
- Sethares, William A. Tunings for 19 Tone Equal Tempered Guitar. 1991.
- Sword, Ron. Enneadecaphonic Scales for Guitar: A Repository of Scales, Chord-Scales, Notations and Techniques for Nineteen Equal Divisions of the Octave. 2010.
- Yasser, Joseph. Theory of Evolving Tonality. 1932.
External links
- 19-tone equal-temperament and 1/3-comma meantone / 19-edo / 19-ed2 on the Tonalsoft Encyclopedia
- Microtonalism by Ingrid Pearson, Graham Hair, Dougie McGilvray, Nick Bailey, Amanda Morrison and Richard Parncutt (from n-ISM, the Network for Interdisciplinary Studies in Science, Technology, and Music)
- Forum Discussion with some 19-EDO xenharmonic scales Hanson (Keemun), Liese, Negri, Magic, Semaphore, Sensi played on guitar.
- Bostjan Zupancic's 19-EDO pages
- Catalog of all 19edo heptatonic scales
Notes
References
- Bucht, Saku and Huovinen, Erkki, Perceived consonance of harmonic intervals in 19-tone equal temperament, CIM04_proceedings.
- Levy, Kenneth J., Costeley's Chromatic Chanson, Annales Musicologues: Moyen-Age et Renaissance, Tome III (1955), pp. 213-261.