Hanson and cata
| Kleismic; hanson; cata |
325/324, 625/624 (2.3.5.13)
((2.3.5.13) 15-odd limit) 2.35c
((2.3.5.13) 15-odd limit) 34 notes
- "Kleismic" redirects here. For the temperament families, see Kleismic family and Kleismic rank three family.
Kleismic, known in the 5-limit as either hanson or simply "kleismic", is a rank-2 temperament and parent of the kleismic family, characterized by the vanishing of the kleisma (15625/15552). It is generated by a classical minor third (6/5), six of which make a twelfth (3/1).
Another useful interpretation of the kleisma as a comma is that it makes the classical chromatic semitone, 25/24, into a third-tone by equating three of this interval to 9/8. As 9/8 = (25/24)(26/25)(27/26), it is natural to equate 25/24 to 26/25 and 27/26 as well, thereby tempering out the marveltwin comma (S25 × S26 = 325/324), and the tunbarsma (S25 = 625/624), resulting in a low-complexity but high-accuracy extension to the 2.3.5.13 subgroup, sometimes known as cata. As the chain of generators naturally gives us hemitwelfths at only 3 generator steps, this also corresponds directly to an interpretation of these as 26/15 (and thus hemifourths as 15/13) by tempering out S26 = 676/675.
Extensions with prime 7 include catakleismic (which adds 225/224, finding 7 at 22 generators up), countercata (which adds 5120/5103, finding 7 at 31 generators down), metakleismic (which adds 179200/177147, finding 7 at 56 generators up), keemun (which adds 49/48, finding 7 at 3 generators up), anakleismic (which adds 2240/2187, finding 7 at 37 generators up), and catalan (which adds 64/63, finding 7 at 12 generators down). Of these, catakleismic can perhaps be considered the canonical, as it makes a natural further equivalence of 25/24~26/25~27/26 to 28/27 and can be defined in the 7-limit by tempering out 225/224 and 4375/4374. However, countercata exists closer to the truly optimal range of kleismic (between 53edo and 87edo) and tempers out 4096/4095 where 65/64 and therefore 64/63 are close to just.
Most of these extensions can also incorporate prime 11 (and thereby reach the full 13-limit) by tempering out 385/384, equating the ~6/5 generator to 77/64, which works well since ~6/5 should be tuned sharp of just, bringing it closer to 77/64, which is in fact just at very close to 15edo's minor third of 320c.
For technical data, see Kleismic family #Hanson.
Interval chain
In the following table, odd harmonics 1–15 are labeled in bold.
| # | Cents* | Approximate ratios |
|---|---|---|
| 0 | 0.0 | 1/1 |
| 1 | 317.1 | 6/5, 65/54 |
| 2 | 634.2 | 13/9, 36/25 |
| 3 | 950.3 | 26/15, 45/26 |
| 4 | 68.4 | 25/24, 26/25, 27/26 |
| 5 | 385.6 | 5/4, 81/65 |
| 6 | 702.7 | 3/2 |
| 7 | 1019.8 | 9/5, 65/36 |
| 8 | 136.9 | 13/12, 27/25 |
| 9 | 454.0 | 13/10 |
| 10 | 771.1 | 25/16, 39/25, 81/52 |
| 11 | 1088.2 | 15/8 |
| 12 | 205.3 | 9/8 |
| 13 | 522.4 | 27/20, 65/48 |
| 14 | 839.6 | 13/8, 81/50 |
| 15 | 1156.7 | 39/20 |
| 16 | 273.8 | 75/64 |
| 17 | 590.9 | 45/32 |
| 18 | 908.0 | 27/16 |
| 19 | 25.1 | 65/64, 81/80 |
* In 2.3.5.13-subgroup CTE tuning
Tunings
Optimized tunings
| Weight-skew\Order | Euclidean | |
|---|---|---|
| Constrained | Destretched | |
| Tenney | (2.3.5) CTE: ~6/5 = 317.0308¢ | (2.3.5) POTE: ~6/5 = 317.007¢ |
| Equilateral | (2.3.5) CEE: ~6/5 = 317.1033¢
(11/61-kleisma) | |
| Tenney | (2.3.5.13) CTE: ~6/5 = 317.1110¢ | (2.3.5.13) POTE: ~6/5 = 317.0756¢ |
| Optimized chord | Generator value | Polynomial | Further notes |
|---|---|---|---|
| 3:4:5 (+1 +1) | ~6/5 = 317.1496 | g6 + 2g5 − 8 = 0 | 1–3–5 equal-beating tuning, close to 8/43-kleisma |
| 4:5:6 (+1 +1) | ~6/5 = 317.9593 | g6 − 2g5 + 2 = 0 | 1–3–5 equal-beating tuning, close to 2/7-kleisma |
| 10:12:15 (+2 +3) | ~6/5 = 317.6675 | g6 − 5g + 3 = 0 | Close to 1/4-kleisma |
| 9:13:15 (+2 +1) | ~6/5 = 317.5679 | 3g3 + 4g − 10 = 0 | Close to 13/36-marveltwin comma |
| 13:15:18 (+2 +3) | ~6/5 = 317.0010 | 3g3 − g − 4 = 0 | Close to 13/51-marveltwin comma |
Tuning spectrum
| EDO generator |
Eigenmonzo (unchanged interval)* |
Generator (¢) | Comments |
|---|---|---|---|
| 6/5 | 315.6413 | Untempered tuning, lower bound of 5-odd-limit diamond tradeoff | |
| 5\19 | 315.7895 | Lower bound of 2.3.5.13-subgroup 15-odd-limit diamond monotone | |
| 27/26 | 316.3343 | 1/4-tunbarsma | |
| 29\110 | 316.3636 | 110ff val | |
| 24\91 | 316.4835 | 91f val | |
| 27/25 | 316.6547 | 1/8-kleisma | |
| 19\72 | 316.6667 | ||
| 9/5 | 316.7995 | 1/7-kleisma | |
| 33\125 | 316.8000 | 125f val | |
| 26/25 | 316.9750 | 1/4-marveltwin comma | |
| 14\53 | 316.9811 | ||
| 3/2 | 316.9925 | 1/6-kleisma | |
| 75/52 | 317.0274 | 1/2-tunbarsma | |
| 51\193 | 317.0984 | ||
| 15/8 | 317.1153 | 2/11-kleisma | |
| 88\333 | 317.1171 | ||
| 13/10 | 317.1349 | ||
| 37\140 | 317.1429 | ||
| 13/8 | 317.1805 | ||
| 60\227 | 317.1807 | ||
| 23\87 | 317.2414 | ||
| 5/4 | 317.2627 | 1/5-kleisma, upper bound of 5-odd-limit diamond tradeoff | |
| 13/12 | 317.3216 | ||
| 32\121 | 317.3554 | ||
| 41\155 | 317.4194 | ||
| 15/13 | 317.4197 | 1/3-marveltwin comma | |
| 9\34 | 317.6471 | ||
| 25/24 | 317.6681 | 1/4-kleisma, virtually DR 10:12:15 | |
| 22\83 | 318.0723 | 83f val | |
| 13/9 | 318.3088 | 1/2-marveltwin comma, upper bound of 2.3.5.13-subgroup 15-odd-limit diamond tradeoff | |
| 125/72 | 318.3437 | 1/3-kleisma | |
| 13\49 | 318.3673 | 49f val | |
| 125/104 | 318.4135 | Full tunbarsma | |
| 625/432 | 319.6949 | 1/2-kleisma | |
| 4\15 | 320.0000 | Upper bound of 2.3.5.13-subgroup 15-odd-limit diamond monotone | |
| 65/54 | 320.9764 | Full marveltwin comma |
* Besides the octave
Other tunings
- DKW (2.3.5): ~2 = 1\1, ~6/5 = 317.1983
Scales
Images
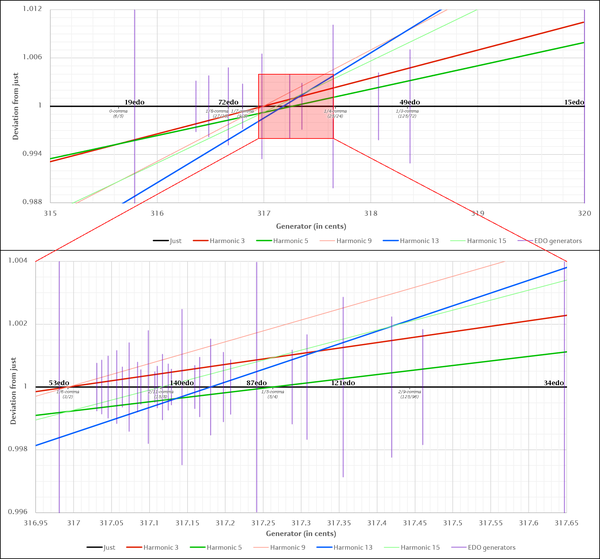
A chart of the tuning spectrum of hanson and cata, showing the offsets of odd harmonics 3, 5, 9, 13, and 15, as a function of the generator; all EDO tunings are shown with vertical lines whose length indicates the EDO's tolerance, i.e. half of its step size in either direction of just, and some small EDOs supporting the temperament are labeled. Comma fractions with corresponding eigenmonzos also labeled.