Kite's color notation
- "Color notation" redirects here. For Dolores Catherino's polychromatic notation system, see Polychromatic system.
Color notation is a musical notation system for just intonation. Features:
- No new symbols: all microtonal inflections are familiar characters; hence they are immediately speed-readable.
- Furthermore, they are all on the QWERTY keyboard, making the notation easily typeable.
- Every microtonal inflection has a spoken name (colorspeak), making the notation speakable.
- Most importantly, one can name not only notes but also intervals. As a result, color notation can name scales, chords, chord progressions, and even prime subgroups and temperaments. Thus it's not merely a notation but a complete nomenclature.
Colorspeak is the term for spoken color notation. It's designed to be easily pronounced no matter what one's native language is and also to be very concise; almost every element of colorspeak is only one short syllable ending with a vowel. The five basic vowels are pronounced /a/, /ɛ/, /i/, /o/ and /u/ (as in ma, met, me, mow, and moo) by an English speaker, but perhaps differently by others (e.g. perhaps /e/ instead of /ɛ/).
Color names for primes 3, 5, and 7
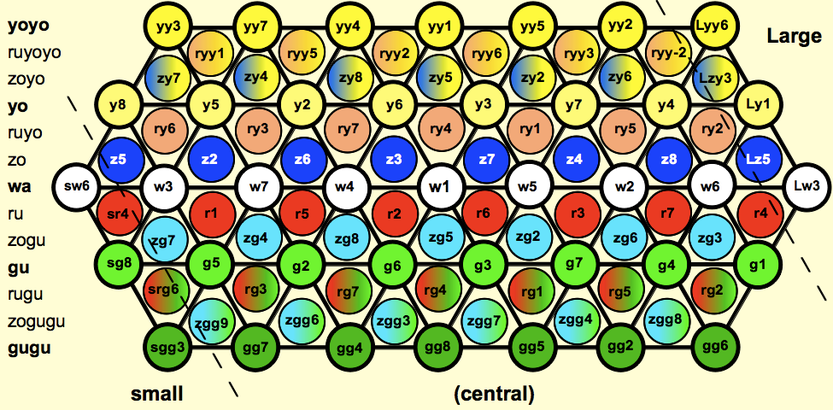
Every prime above 3 has two colors, an over color (prime in the numerator) and an under color (prime in the denominator). Over colors end with -o and under colors end with -u. The color for 3-limit ends in -a for all, which includes over (3/2, 9/8), under (4/3, 16/9) and neither (1/1, 2/1).
| 3-all | = wa /wa/ = white (strong but colorless) = often perfect |
| 5-over | = yo /jo/ ("yo") = yellow (warm and sunny) = often major |
| 5-under | = gu /gu/ ("goo") = green (not as bright as yellow) = often minor |
| 7-over | = zo /zo/ = blue/azure (dark and bluesy) = often subminor |
| 7-under | = ru /ru/ = red (alarming, inflamed) = often supermajor |
The colors make a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 – 5/4 – 6/5 – 7/6. (Those who associate these ratios with different colors can ignore the rainbow metaphor and think of w, y, g, etc. as arbitrary consonants.) Colors are abbreviated as w, y, g, z, and r. Use z (azure or Spanish/Portuguese azul), not b (blue), because b already means flat. Mnemonic: Z looks like 7 with an extra line on the bottom.
Interval names
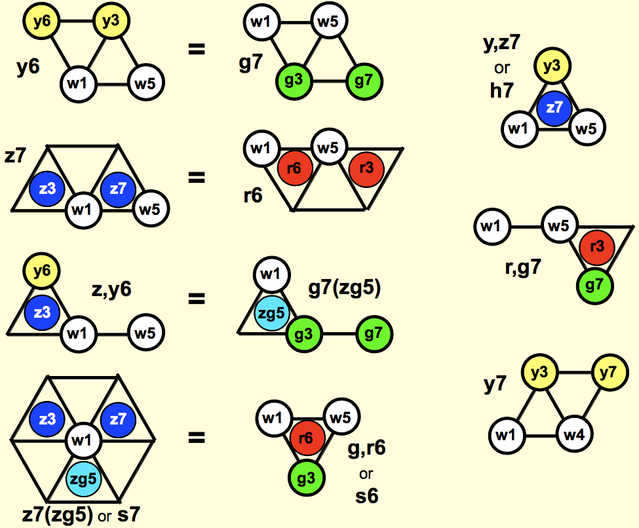
A color and a degree indicate a ratio, and vice versa. Every ratio has a spoken name and a written name. For 3/2, they are wa 5th and w5. Colors and degrees always add up predictably: z3 + g3 = zg5 = zogu 5th. Zogu, not guzo; higher primes always come first. Opposite colors cancel: y3 + g3 = w5.
The JI lattice consists of many rows, each one a chain of 5ths. Each row has its own color, and each color has its own row.
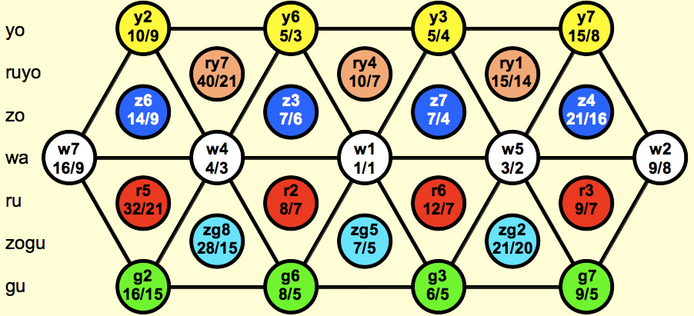
If two ratios have the same color, their prime-counts aka monzos differ only in the first two numbers. For example, all zogu ratios have a prime-count of the form [a b -1 1⟩.
The following table lists all the intervals in this lattice. See the gallery of just intervals for many more examples.
| Ratio | Prime-count | Cents | Color & degree | |
|---|---|---|---|---|
| 1/1 | [0 0⟩ | 0 ¢ | wa unison | w1 |
| 21/20 | [-2 1 -1 1⟩ | 84 ¢ | zogu 2nd | zg2 |
| 16/15 | [-4 1 1⟩ | 112 ¢ | gu 2nd | g2 |
| 15/14 | [-1 1 1 -1⟩ | 119 ¢ | ruyo unison | ry1 |
| 10/9 | [1 -2 1⟩ | 182 ¢ | yo 2nd | y2 |
| 9/8 | [-3 2⟩ | 204 ¢ | wa 2nd | w2 |
| 8/7 | [3 0 0 -1⟩ | 231 ¢ | ru 2nd | r2 |
| 7/6 | [-1 -1 0 1⟩ | 267 ¢ | zo 3rd | z3 |
| 6/5 | [1 1 -1⟩ | 316 ¢ | gu 3rd | g3 |
| 5/4 | [-2 0 1⟩ | 386 ¢ | yo 3rd | y3 |
| 9/7 | [0 2 0 -1⟩ | 435 ¢ | ru 3rd | r3 |
| 21/16 | [-4 1 0 1⟩ | 471 ¢ | zo 4th | z4 |
| 4/3 | [2 -1⟩ | 498 ¢ | wa 4th | w4 |
| 7/5 | [0 0 -1 1⟩ | 583 ¢ | zogu 5th | zg5 |
| 10/7 | [1 0 1 -1⟩ | 617 ¢ | ruyo 4th | ry4 |
| 3/2 | [-1 1⟩ | 702 ¢ | wa 5th | w5 |
| 32/21 | [5 -1 0 -1⟩ | 729 ¢ | ru 5th | r5 |
| 14/9 | [1 -2 0 1⟩ | 765 ¢ | zo 6th | z6 |
| 8/5 | [3 0 -1⟩ | 814 ¢ | gu 6th | g6 |
| 5/3 | [0 -1 1⟩ | 884 ¢ | yo 6th | y6 |
| 12/7 | [2 1 0 -1⟩ | 933 ¢ | ru 6th | r6 |
| 7/4 | [-2 0 0 1⟩ | 969 ¢ | zo 7th | z7 |
| 16/9 | [4 -2⟩ | 996 ¢ | wa 7th | w7 |
| 9/5 | [0 2 -1⟩ | 1018 ¢ | gu 7th | g7 |
| 28/15 | [2 -1 -1 1⟩ | 1081 ¢ | zogu octave | zg8 |
| 15/8 | [-3 1 1⟩ | 1088 ¢ | yo 7th | y7 |
| 40/21 | [3 -1 1 -1⟩ | 1116 ¢ | ruyo 7th | ry7 |
| 2/1 | [1 0⟩ | 1200 ¢ | wa octave | w8 |
Yo and ru intervals tend to be major, and gu and zo ones tend to be minor. But interval quality is redundant (if a third is yo, it must be major), it's not unique (there are other major thirds available), and quality isn't used with color names (see #Color Names for Higher Primes below for why). Intervals on the lattice's far right and far left are called not augmented and diminished but large and small, written as L and s, and abbreviated as la and sa. La and sa can always be distinguished from solfege's La and saregam's Sa by context. Central, the default, means neither large nor small. This lattice shows the boundaries between the large, small and central zones:
The general term for large/small/central is magnitude. Only intervals have a magnitude, notes never do, and L and s never appear on the staff. A ratio's magnitude is the sum of all the prime-counts except the first one, divided by 7, and rounded off. 0 = central, 1 = large, 2 = double large, etc. 81/64 = [-6 4⟩, and 4/7 rounds to 1, so 81/64 is a lawa 3rd = Lw3. Similarly, 135/128 = [-7 3 1⟩ is a layo unison = Ly1. Unfortunately, magnitudes do not add up predictably like colors and degrees: w2 + w2 = Lw3.
Colors can be doubled or tripled, which are abbreviated bi- ("bee", /bi/) and tri- ("tree", /tɹi/): 49/25 is a bizogu 9th = zzgg9, and 128/125 is a trigu 2nd = ggg2. Bi- is only used if it shortens the name: 25/16 is a yoyo 5th, not a biyo 5th. Likewise with magnitudes: double-large is lala and triple-large is trila. For quadruple, etc., see #Exponents.
Colors using only one prime above 3 are called primary colors. Thus gu and yoyo are primary and ruyo is non-primary.
Degrees can be negative: 50/49 = 35¢ is a biruyo negative 2nd = rryy-2. It's negative because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd.
Compound, abbreviated co- or c, is a conventional music theory term that means widened by an octave. 15/4 is a compound yo 7th = coyo 7th = cy7. 5/1 is a double-compound yo 3rd = cocoyo 3rd = ccy3. More examples in the Gallery of just intervals. Mnemonic: co- as in co-pilot means auxiliary, thus a 9th is a co-2nd. See #Prime Subgroup Names below for another mnemonic.
Note names
Notes are named zEb, yyG#, etc. spoken as "zo E flat" and "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa.
Adding gu raises a note by 81/80, and adding yo lowers it. Adding ru raises it by 64/63, and adding zo lowers it. Mnemonic: gu and ru go up, and yo and zo go down. But beware, this under/up correlation is just a coincidence. (A mapping comma is always up, and the first two mapping commas happen to be -under commas, but half of the time they will be -over commas.)
The relative-notation lattice above can be mentally superimposed on this absolute-notation lattice to name every note and interval. For example, D + y3 = yF#, and from yE to ryF# = r2.
Prime subgroup names
Just as wa means 3-all or 3-limit, ya means 5-all and includes wa, yo, gu, yoyo, gugu, etc. Ya refers to the 2.3.5 prime subgroup = 5-limit. Za = 7-all refers to 2.3.7 = no-fives 7-limit. Yaza refers to 2.3.5.7 = the full 7-limit. Nowa means without wa, and yaza nowa = 2.5.7.
Prime 2 (even more colorless than wa) is clear, abbreviated ca, and yaza noca = 3.5.7 = Bohlen–Pierce. 2-limit intervals like 2/1 are called wa not clear, for simplicity. Nowaca means without 2 or 3, thus 5.7.11 is yazala nowaca. Clear/ca is only ever used in the terms noca and nowaca, and in certain theoretical discussions. However, an additional mnemonic for "co-" (compound, widened by an octave) is "clear-over", in the sense that the ratio's numerator is multiplied by 2.
More on prime subgroups in the next section.
Color names for higher primes
Colors for primes greater than 7 are named after the number itself, using the prefix i- for disambiguation as needed:
Lo = 11-over, lu = 11-under, and la = 11-all = 2.3.11. Because "lo C" sounds like "low C", lo when by itself becomes ilo "ee-LOW" (/ilo/). But when with other syllables, it doesn't need i-, as in 11/7 = loru 5th. La when by itself becomes ila, to avoid confusion with the solfege note La, and also with La for large. Sans serif fonts like the one you're reading right now conflate upper-case-i with lower-case-L, so ilo and ila are capitalized as iLo and iLa rather than Ilo and Ila. iLo and lu are abbreviated to 1o and 1u both on the score and in interval names and chord names, e.g. ilo A = 1oA, ilo 4th = 1o4 = 11/8, and C ilo seven = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. Lolo is written 1oo. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both ilo and lu, since they are only 7.1 ¢ apart. Lavender is a pseudocolor that implies the Lulu aka Neutral temperament. iLo notes could be called lovender, and lu notes could be called luvender. Both are "shades" of lavender.
Tho (/θ/ as in "thirteen") = 13-over, thu = 13-under, and tha = 13-all. Tho and thu are abbreviated as 3o and 3u on the score and in interval names, e.g. 13/8 is a tho 6th = 3o6 and 14/13 is a thuzo 2nd = 3uz2. Thuthu is written 3uu.
Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13, and yazalatha = 2.3.5.7.11.13 = the full 13-limit. Noya is a descriptive adjective, not used in actual prime subgroup names, that indicates the absence of 5 and the presence of higher primes, e.g. zala, latha and zalatha are all noya. Likewise, there's noza, noyaza, etc.
On the score and in note names, the 1o inflection either raises by 33/32 or lowers by 729/704, i.e. 11's mapping comma can vary. The meaning will usually be clear from context, however it's safer to write at the top of the page either "1o4 = P4" or "1o4 = A4". Likewise, 3o6 should be noted as either m6 or M6. While the note 11/8 above C can be written two ways, either as 1oF or as 1oF#, the interval 11/8 can only be written one way, as 1o4. Likewise, 13/8 above C is either 3oA or 3oAb, but 13/8 is only 3o6. This is the primary rationale for using large/small/central rather than major/minor. 11/9 is ambiguously major or minor, but unambiguously central. Intervals names and chord names become unambiguous for la and tha intervals. Another rationale is that commonly used intervals and chords are all central, and get concise names: gu 3rd not gu minor 3rd, E gu not E gu minor, etc. (see #Chord Names below).
So = 17-over, su = 17-under, and sa = 17-all, abbreviated as 17o, 17u and 17a. Iso is an alternate form of so, to distinguish it from the solfege syllable So. 17/12 = 17o5 = iso So. Isa is an alternate form of sa, to distinguish it from sa for small, and from the Indian saregam syllable Sa.
No = 19-over, nu = 19-under, and na = 19-all, abbreviated as 19o, 19u and 19a. Ino is an alternate form of no, because "no 3rd" could mean either 19/16 or thirdless. Inu is an alternate form of nu, to distinguish "the nu chord" from "the new chord".
One might be tempted to write ilo as 11o instead of 1o. This would work on a score, but would be confusing in chord names. The triad C11o would look like a diminished 11th chord. Color notation avoids naming primes with the numbers found in chord names, which are 2 4 5 6 7 9 11 and 13. Thus tho is 3o not 13o, iso is 17o not 7o, and ino is 19o not 9o.
The prefix i- is only used when confusion is possible. Thus 19/15 = nogu 4th not inogu 4th.
Twetho = 23-over, twethu = 23-under, and twetha = 23-all, abbreviated as 23o, 23u and 23a. 2.3.5.7.23 = yazatwetha = yaza23a. 23/16 is a twetho 5th = 23o5, and 23/22 is a twetholu 2nd = 23o1u2. 529/512 = 23oo2 = bitwetho 2nd (not twethotho, because that means 23-over 13-over).
Similarly, tweno/-nu/-na = 29o/29u/29a, thiwo/-wu/-wa = 31o/31u/31a, etc. The abbreviations are twe-, thi-, fo-, fi- and si-. Note that wa by itself means 3-limit, but -wa as a suffix means "-one-all".
| prime | 5/4 | 7/4 | 11/8 | 13/8 | 17/16 | 19/16 | 23/16 | 29/16 | 31/16 | 37/32 | 41/32 | 43/32 | 47/32 | 53/32 | 59/32 | 61/32 | 67/64 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y3 | z7 | 1o4 | 3o6 | 17o2 | 19o3 | 23o5 | 29o7 | 31o7 | 37o3 | 41o3 | 43o4 | 47o5 | 53o6 | 59o7 | 61o7 | 67o2 | |
| word | yo | zo | (i)lo | tho | (i)so | (i)no | twetho | tweno | thiwo | thiso | fowo | fotho | foso | fitho | fino | siwo | siso |
| on the score |
M3 | m7 | P4 or A4 | m6 or M6 | m2 | m3 | d5 | m7 | M7 | m3 | M3 | P4 | P5 | M6 | M7 | M7 | m2 |
Mnemonic (sung to the tune of "Supercalifragilisticexpialidocious"):
Yaza latha sana twetha twena thiwa thisa / Fowa fotha fosa fitha fina siwa sisa
Unfortunately seventy can't become se- because that already means 17-fold (see #Exponents below). Setho means 17-fold 13-over, so it can't mean 73-over. So starting at 71, one might use the longer form: 71o is seventy-wo, 73o is seventy-tho, etc. 103o is hundred-tho and 113o is one-ten-tho. Or one might use these terms:
| prime | 71/64 | 73/64 | 79/64 | 83/64 | 89/64 | 97/64 | 101/64 | 103/64 | 107/64 | 109/64 | 113/64 | 127/64 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 71o2 | 73o2 | 79o3 | 83o4 | 89o4 | 97o5 | 101o6 | 103o6 | 107o6 | 109o6 | 113o7 | 127o8 | |
| word | fitwewo | fitwetho | fitweno | fithitho | fithino | fifoso | fifiwo | fifitho | fifiso | fifino | fisitho | sisiso |
Note that 23/16 = 628 ¢ is a 5th, not a 4th (but see po & qu below). Furthermore, 31/16 = 1145 ¢ is a 7th not an 8ve, and 37/32 = 251 ¢ is a 3rd not a 2nd. For any prime P, the degree of the ratio P/1 is chosen to minimize negative intervals. It is determined by its 8ve-reduced cents, and how it relates to 12edo:
| unison | 2nd | 3rd | 4th | 5th | 6th | 7th | 8ve |
|---|---|---|---|---|---|---|---|
| 0-50 ¢ | 50-250 ¢ | 250-450 ¢ | 450-600 ¢ | 600-750 ¢ | 750-950 ¢ | 950-1150 ¢ | 1150-1200 ¢ |
This makes the "pseudo-edomapping" <7 11 16 20 24 26 29 30 32 34 37...]. An alternative method would use the actual 7edo edomapping, but that requires using every other 14edostep as boundaries, harder to remember and much less convenient than the 24edo boundaries used here. Since negative intervals will arise no matter what, convenience is prioritized. For the first 26 primes, the 24edo-based degrees correspond to 7klmrs-edo.
Exponents
Exponent syllables aka multiplier syllables provide a way to shorten names that have repeated syllables. For example, 250/243 = [1 -5 3⟩ is a yoyoyo unison which shortens to triyo unison. Exponents can also apply to magnitudes (triple-small is trisa) and octaves (triple-compound is trico).
The triyo unison can be written as y31 for, but it's more convenient (as well as closer to the spoken form) to write 3y1. Trilo is written 3(1o) to distinguish it from 31o, thirty-one-over.
We've seen bi- for double and tri- for triple. Quadruple and quintuple are abbreviated quad- and quin-, as in quadyo or quingu. Colorspeak syllables usually end in one of the five basic vowels. Quad and quin are both exceptions, so quad may optionally be spoken as "kwah" (/kwä/), and quin as "kwee" (/kwi/).
Except for quad, all exponent syllables are prime numbers. Septuple is sep-. Above 7, all exponent syllables are the root color word plus -e for exponent. Eleven-fold is le- = "eleven exponent", pronounced as in "lens". Thirteen-fold is the- as in "thesaurus". Note that sep- means seven-fold and se- means seventeen-fold.
Exponents can be combined: sextuple = tribi-, 8-fold = quadbi-, 9-fold = tritri-, 10-fold = quinbi-, 12-fold = quadtri-, 14-fold = sepbi-, 15-fold = quintri-, 16-fold = quadquad-, etc. The component syllables are simply the number's prime factors in descending order, except that quad replaces bibi and comes before tri.
Exponents affect all subsequent syllables until the -a- delimiter occurs: trizogu = 3zg is triple-zo triple-gu, but trizo-agu = 3zag is triple-zo single-gu. The "a" in la- and sa- also acts as a delimiter: trilayo = 3Ly is triple-large single-yo. (Triple-large triple-yo would be trila-triyo = 3L3y.)
Long color names use hyphens to make the name easier to parse. There are strict rules for hyphenation, to ensure uniformity.
- Put a hyphen before every -a- delimiter
- Put a hyphen after the magnitude (after the final la- or sa-)
- Put a hyphen after coco-, trico-, etc.
- Put a hyphen before and after "seventy", "eighty", etc.
The hyphen is generally omitted if it would create a subunit of 1 syllable. Thus despite the 2nd rule, layo, lalagu and sagugu are all unhyphenated. And despite the 3rd rule, coyo, cozogu and cocowa are unhyphenated. However, the last rule always holds, e.g. 284/243 = 22 * 3-5 * 71 is a sa-seventy-wo 3rd.
Converting a ratio to/from a color name
Often a ratio can be converted by breaking it down into simpler ratios with familiar color names, then adding. For example, 45/32 is 5/4 times 9/8, which is y3 plus w2. The colors and degrees are summed, making y4. But is it y4 or Ly4? The magnitude is not summed, and must be found either visually from the lattices above, or from the prime-count vector or PCV directly. 45/32 = [-5 2 1⟩, and (2+1)/7 rounds to 0, so it's central, and 45/32 = y4.
For more complex ratios, a more direct method is needed:
Converting a ratio: Find the PCV by prime factorization. To find the color, combine all the appropriate colors for each prime > 3, higher primes first. To find the degree, first find the stepspan, which is the dot product of the PCV with the "pseudo-edomapping" discussed above <7 11 16 20 24 26 29 30...]. Then add 1, or subtract 1 if the stepspan is negative. To find the magnitude, add up all the prime counts except the first one, divide by 7, and round off. Combine the magnitude, color and degree to make the color name. If the interval is > 1200 ¢, octave-reduce as desired (e.g. a 9th may or may not become a compound 2nd). Add one co- prefix for every octave removed. Combine repeated syllables so that three yo's becomes triyo, etc. For the exact combination "grammar", see Color notation/Temperament Names.
Example: ratio = 63/40
- PCV = [-3 2 -1 1⟩
- Color = zogu
- Stepspan = ⟨7 11 16 20 | -3 2 -1 1⟩ = -21 + 22 - 16 + 20 = 5 steps
- Degree = 5 + 1 = a 6th
- Magnitude = round [(2 + (-1) + 1) / 7] = round (2/7) = 0 = central
- Interval = zogu 6th or zg6 (63/20 would be zg13 = czg6)
Converting a color name: Let S be the stepspan of the interval, S = degree − sign (degree). Let M be the magnitude of the color name, with L = 1, LL = 2, etc. Small is negative and central is zero. Let C be the number of "co-" prefixes. Let the PCV be [a b c d e …⟩. The colors directly give you all the prime counts except for a and b. Let S' be the dot product of [0 0 c d e …⟩ with the pseudo-edomapping. Let M' = round((2(S − S') + c + d + e + ...) / 7). Then a = −3 (S – S') – 11 (M – M') + C and b = 2 (S − S') + 7 (M − M'). (Derivation here) Convert the PCV to a ratio.
Example: interval = sgg2 = sagugu 2nd
- S = 2 - 1 = 1 step, M = small = -1, C = 0. PCV = [a b -2⟩
- S' = ⟨7 11 16 | 0 0 -2⟩ = -32. S - S' = 1 - (-32) = 33.
- M' = round ((2·33 + (-2)) / 7) = round (64 / 7) = 9. M - M' = -1 - 9 = -10.
- a = -3 (S - S') - 11 (M - M') + C = -3·33 - 11·(-10) + 0 = -99 + 110 = 11.
- b = 2 (S - S') + 7 (M - M') = 2·33 + 7·(-10) = 66 - 70 = -4
- PCV = [11 -4 -2⟩, ratio = 2048/2025.
Chord names
Triads are named after their 3rd, e.g. a yo chord has a yo 3rd. A yo chord rooted on C is a Cy chord = "C yo" = C yE G. Qualities such as major and minor aren't used, because a chord with an 11/9 3rd is hard to classify. Thirdless dyads are written C5 = w1 w5 or C(zg5) = w1 zg5. The four main yaza triads:
Tetrads are named e.g. "C yo-six" = Cy6 = C yE G yA. The 11 main yaza tetrads, with chord homonyms (same shape, different root) equated:
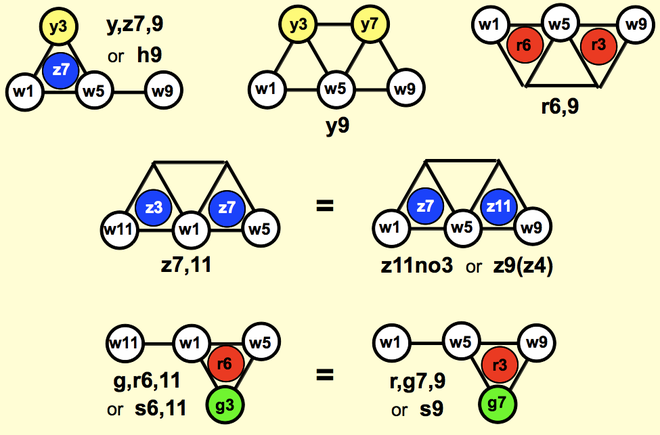
A 9th chord contains a 3rd, 5th and 7th. An 11th chord contains all these plus a 9th. A 13th chord contains all these plus an 11th. The 5th, 9th and/or 13th default to wa. The 6th, 7th, and/or 11th default to the color of the 3rd. Mnemonic: every other note of a stacked-thirds chord is non-wa: 6th-root-3rd-5th-7th-9th-11th-13th. Thus Cy13 = w1 y3 w5 y7 w9 y11 w13, and Cy9 and Cy11 are subsets of this chord. However, an added 11th defaults to wa, as in z7,11:
Alterations are always in parentheses, additions never are, e.g. z7(zg5) and z,y6. An alteration's degree must match a note in the chord, e.g. Cz7(y6) is invalid. But an exception is made for sus chords, where degree 2 or 4 alter the 3rd. The sus note defaults to wa. A 6:8:9 chord could be written C(4), but the parentheses rule is relaxed to allow the conventional C4. Likewise 8:9:12 is C2. But if the sus note isn't wa, parentheses must be used. Thus w1 z4 w5 = C(z4) = "C zo-four". More examples:
- 6:7:8:9 = Cz,4 = "C zo add-four"
- w1 w4 w5 y7 w9 = Cy9(4) = "C yo-nine sus-four"
- w1 z4 w5 z7 = Cz7(z4) or C(z4)z7 = "C zo-seven zo-four" or "C zo-four zo-seven"
Omissions are indicated by "no". The za Hendrix chord is Ch7z10no5. (To write it as a sharp-9 chord, see po and qu below.) A no3 tetrad can also be written as a 5 chord with an added 6th or 7th: Cy6no3 = C5y6, and Cz7(zg5)no3 = C(zg5)z7.
The y,z7 chord is called the h7 chord ("har-seven"), because it's part of the harmonic series. Ch9 = Cy,z7,9 and Ch11 = Cy,z7,w9,1o11. The s7 ("sub-seven") chord is part of the subharmonic series. It's the first 7 subharmonics, with the 7th subharmonic becoming the root. Cs9 = Cr,g7,9 and Cs11 = C1o11(1or5,1og9). Note that s9 is not s7 plus a 9th, but a completely different chord. Usually the 9th ascends from the root, but in a sub9 chord it descends from the top note, and becomes the new root. Thus the s7 chord is contained in the upper four notes of the s9 chord, not the lower four.
Cs6 = Cg,r6 = 12:10:8:7. Other than the s6 chord, all harmonic/subharmonic numbers must be odd, e.g. Ch6 and Ch8 are invalid. For any odd number N greater than 5, ChN is 1:3:5...N and CsN is N...5:3:1. Additions, alterations and omissions refer to degrees, not harmonics or subharmonics: Ch7,11 adds w11, not 1o11. Ch9no5 omits w5, not y3. However, all numbers > 13 refer to (sub)harmonics, e.g. Ch9,15 adds y7 and Ch19no15 omits it.
All wa chords can be named conventionally, since wa is the default color. Thus w1 – w3 – w5 is both Cw and Cm. And w1 – Lw3 – w5 – w6 is both CLw6 and C6. For aesthetic reasons, the conventional name is preferred only when neither "M" nor "m" appears in the name (since color notation doesn't use major/minor). This is especially true if the chord includes non-wa notes: w1 – w3 – w5 – y6 is Cw,y6 not Cm,y6.
Chords can be classified as bicolored (e.g. g7 or r6), tricolored (e.g. z7(zg5) or z,y6), quadricolored (e.g. s6(zg5) or h7,zg9), etc.
Chord progressions, keys, scales and modulations
A conventional chord name like IIm7 names the chord root relative to the tonic and the chord notes relative to the chord root. The "m7" is shorthand for (P1, m3, P5, m7). Adding each of these intervals to the M2 root gives us the four notes of the chord: M2, P4, M6 and P8. In the key of E, it would be F#m7 = F# + (P1, m3, P5, m7) = F#, A, C# and E.
Color notation works the same way. The tonic is always wa. The root of each chord has a color, which defaults to wa. C - Am - F - G7 might become Cy - yAg - Fy - Gy,w7, spoken as "C yo, yo A gu, F yo, G yo wa-seven". If the root isn't wa, the root color is added to each interval's color. Yo and gu cancel out when added together, so yAg = yA + (w1, g3, w5) = yA + wC + yE. The chord's third is gu relative to the chord root, but wa relative to the tonic.
In relative notation, the previous example becomes Iy - yVIg - IVy - Vy,w7, spoken as "one yo, yo-six gu, four yo, five yo wa-seven". Never use lower-case roman numerals for minor chords: ii becomes IIg or IIz. A IIIy chord has a w3 root, which is 32/27 not 81/64. The latter would be a LwIIIy chord (use L and s, not # and b; #IIIy is invalid).
In adaptive JI, chords are just, but roots move by tempered intervals. Comma pumps are indicated with brackets roughly halfway through the pump: Cy - yAg - [y=w]Dg - Gy - Cy. The pattern is [old=new]: the previous chord implies yDg and the following chord implies wDg. See Comma pump examples.
Keys and scales are loosely named after the colors used. Wa is assumed present. In 5-limit JI, the key of A minor is A gu and the scale is the gu scale. The Bbh7 - Ebh7 - Bbh7 - Fh9 example in the staff notation section is in Bb yo-zo. The centaur scale is yo-zo-zogu. Like chords, scales can be classified as bicolored (A gu), tricolored (Bb yo-zo), quadricolored (centaur), etc.
Scales can be named more precisely analogous to how chords are named. The tonic, 2nd, 4th and 5th default to wa. Thus a yo scale is w1 w2 y3 w4 w5 y6 y7 w8. If the 2nd were instead yo, it would be a yo yo-2 scale, written y(y2). If the 2nd is sometimes yo, sometimes wa, the scale is yo plus yo-2, written y+y2. (A hexatonic scale might use "minus".) The 5-limit harmonic minor scale is gu yo-7. The Bbh7 - Ebh7 - Bbh7 - Fh9 scale is Bb yo plus zo-3-4-7, written Bb y+z347.
(Occasionally, the 6th or the 7th may be La or sa. For example, the wa scale has a wa 3rd, because the 3rd of the scale always matches the scale name exactly. The 6th and 7th default to a perfect 4th/5th from the 3rd, so the 6th is sa, not central. Thus the wa scale is minor, and the Lawa scale is major.)
Just as there is a har7 chord, there is a har15 scale: w1 w2 y3 1o4 w5 3o6 z7 y7 w8. A har-N scale (where N is odd) is harmonics (N+1)/2 to N+1. The tonic of the scale is always a power of 2. Thus the har9 scale is not 5:6:7:8:9:10 but 8:9:10:12:14:16 = w1 w2 y3 w5 z7 w8. The 5:6:7:8:9:10 scale is the over-5 mode of this scale, written "har9 /5". Since there are no gaps in the harmonic series fragment, 5:6:7:8:9:10 can be abbreviated as 5::10. Likewise there are subharmonic scales and modes. The sub15 scale is 16:15:14:13:12:11:10:9:8 or 16::8. The notes are w1 g2 r2 3u3 w4 1u5 g5 w7 w8.
A pentatonic scale is assumed to be a major or minor pentatonic scale with an altered 3rd, 6th or 7th. Yo and ru imply a major pentatonic scale, and zo and gu imply minor. Thus zo pentatonic = w1 z3 w4 w5 z7 w8. Wa, ila or tha pentatonic scales need to specify major or minor, e.g. ilo major pentatonic = w1 w2 1o3 w5 1o6 w8 and ilo minor pentatonic = w1 1o3 w4 w5 1o7 w8. Hemitonic scales can be named e.g. yo minor pentatonic = w1 y3 w4 w5 y7 w8 or zo major pentatonic = w1 w2 z3 w5 z6 w8.
Analogous to the relative and parallel major or minor, one can modulate to relative gu, parallel ru, etc. Modulating from a yo key to the relative gu means using gu chords on yo roots. Modulating from yo to the parallel gu means using gu chords on wa roots. Going from yo zo to the relative gu means using chords with gu and/or ru in them on yo roots. Going to the relative ru means using the same chords on zo roots. Going from yo zo to the parallel gu ru means using the same chords on wa roots. One can also modulate fourthward or fifthward, abbreviated 4thwd or 5thwd. Modulating in either direction is modulating waward. Modulating from a yo key to the relative gu, and perhaps from there to the parallel yo is modulating yoward. A root movement by a yo interval (e.g. Iy - yVIg) is a yoward move. Likewise, there's guward, and yaward includes both. Likewise, there's zoward, ruward, zaward, iloward, etc.
Staff notation
Notes on the staff default to wa. Non-wa notes have a color inflection like g, ry, etc. Like conventional sharp/flat accidentals, they apply to every such note in the measure and in the same octave. Unlike conventional accidentals which apply to a note (e.g. A), color inflections only apply to one specific "version" of that note (e.g. A flat or A natural). For example, the yo inflection in the first chord applies to all the D-naturals in that measure, but not to the D-flats.
L and s never appear on the staff. Tripled colors are written as 3y not yyy. In MuseScore, color inflections are made by adding fingerings to the notes, then editing the fingering text. A fingering can be copied from one note and pasted to another note. The font used here is Arial Black.
This 10-page score of "Evening Rondo" uses the free open-source font Petaluma Script. The letters are 9pt, except that a "z" between two staff lines is 8pt. File:Evening Rondo colors.pdf
Color signatures
Key signatures are generally standardized, so as to be extremely speed-readable. Thus a piece that uses the D harmonic minor scale won't have a key signature of Bb and C#, but rather just Bb, and every C in the score will be individually sharpened.
Color signatures are likewise standardized using the same rule for naming chords and scales. The tonic, 2nd, 4th and 5th are all one color, and the 3rd, 6th and 7th are all another color. The color signature is written on the staff next to the conventional key signature using a triple stack and/or a quadruple stack of color inflections, similar to the arrow stacks of ups and downs notation. For example, the "Evening Rondo" score linked above uses a key signature of one sharp and a color signature of a triple stack of zo's to indicate an E zo scale. Another example, a triple stack of yo's would make color notation more similar to Johnston notation.
The tonic always starts off wa, but a piece can modulate to a non-wa tonic. For example, one might start in C yo (triple yo-stack) but modulate yowards to yo A gu (quadruple yo-stack) and then to yo A yo (quadruple yo-stack and triple yoyo-stack). Every triple stack always has the same shape, so that it can be parsed as a single object. Likewise for quadruple stacks.
A color signature can instead be written out explicitly above the staff. This method is less readable but more powerful. Here D and Db have different colors, which wouldn't be possible using color stacks.
Po and qu
Po and qu (/ku/) (short forms p and q) are two optional inflections that indicate raising/lowering by a pythagorean comma. (Mnemonics: p stands for pythagorean, and q is the mirror image of p.) Why would one want to do that? Because by first subtracting that comma and then adding it on again, one can rename a note as another note. This is similar to Sagittal notation (see Sagittal-JI-Translated-To-Colors.png).
For example, F# minus a pythagorean comma is Gb. And Gb plus a pythagorean comma is po Gb. Thus an alternate name for F# is po Gb. Adding po raises the degree by one. The new note name is always a 12edo equivalent of the old note name. Adding qu lowers the degree: Gb = qu F#. If one is resolving from 31oGb to G, one can rename 31oGb as 31oqF# = thiwoqu F sharp.
Subtracting po lowers the degree. Thus ruyopo Db = ruyo C#.
Po and qu can be used with intervals as well. A ruyo unison becomes a ruyopo 2nd. Neither the color nor the magnitude changes.
One reason to change the degree is for ease of naming chords. For example, the za Hendrix chord is Ch7z10no5. To write it as a sharp-9 chord, use qu: Ch7zq9no5.
Another reason is to avoid an awkward unison trill. 
Temperament names and comma names
Temperaments are named after the comma(s) they temper out. Commas are named using an alternate format that omits the degree. 81/80 is the Gu comma, with the "G" capitalized to distinguish it from the gu color, which includes many ratios. Tempering out Gu creates Meantone or Guti or gT, where "-ti" and "T" stand for temperament. 2048/2025 is the Sagugu comma sgg2, and Srutal is Saguguti or sggT. Porcupine is Triyoti or 3yT. Certain commas over 90 ¢ use the -bi- syllable (see the main article for details). For example, Schismic is Layoti or LyT, but Mavila is Layobiti or Ly#2T. Certain wa commas use yet another alternate format, e.g. Mercator's comma is Wa-53 or w-53.
Multi-comma temperaments have multiple commas in their name. Septimal Meantone is Gu & Ruyoyo and Dominant Meantone is Gu & Rugu (-ti can be omitted when the ampersand is used). Untempered primes are included with a plus sign. The 2.3.5.7 prime subgroup with 81/80 tempered out is Guti + za = gT+z, and Blackwood is Sawa + ya = swT+y.
MOS and MODMOS scales can be named as e.g. Triyoti[8]. Individual modes can be named as 2nd Triyoti[8], 3rd Triyoti[7] b7, etc. See Genchain mode numbering.
Ups and downs, lifts and drops, plain and mid
Color notation merely renames ratios more conveniently, and strictly speaking, it only applies to just intonation. However, ratios are often used to loosely describe intervals in edos, and colors can be used as well. A more precise notation uses ups and downs (^ and v) as "virtual colors", inflections that always map to exactly one edostep. Ups and downs are used on the score just like color inflections are. Notes are named e.g. up C sharp = ^C#. Sharp-1 and flat-1 edos don't require ups and downs.
Unlike actual colors, virtual colors generally add up to something simpler, e.g. three of 22edo's ups adds up to an A1. Unlike actual colors, virtual colors combine with major, minor, etc. Intervals are named upmajor 3rd = ^M3, up 4th = ^4, downaug 5th = vA5, etc.
Plain means neither up nor down, analogous to natural meaning neither sharp nor flat. Mid, abbreviated ~, means exactly midway between major and minor. The mid 4th is midway between perfect and augmented, i.e. halfway-augmented, and the mid 5th is halfway-diminished. There is no mid unison or octave. Mid simplifies 72edo notation: m2, ^m2, v~2, ~2, ^~2, vM2, M2. Mid is only used in relative notation, it never applies to notes and never appears on the staff. In 24-edo or 31-edo, the 3rd of C~ is vE or ^Eb, but in 41-edo, it's vvE or ^^Eb.
Chords are named similarly to color notation, with the various qualities downmajor, upminor, mid, etc. replacing colors. Major is the default quality, thus C = C major and Cv = C downmajor. The 6th, 7th and 11th inherit their quality from the 3rd, thus C upminor 9th = C ^Eb G ^Bb D. Chord roots can have ups and downs, as in Cv - Gv - vA^m - Fv or Iv - Vv - vVI^m - IVv. In roman numeral notation, chord roots can be downflat, mid, etc., as in Iv7 - vbIII^m6 - IVv7 or I~7 - ~III - V7. Lower-case roman numerals are never used for minor chords, because vii could mean either seven-minor or down-two-minor. Instead vii is written either VIIm or vIIm. See the notation guide for edos 5-72
Rank-2 temperaments can be notated with ups and downs as well. Plain and mid are also used in this context. Certain temperaments require an additional pair of virtual colors, lifts and drops (/ and \). Notes are named lift C = /C, downdrop F sharp = v\F#, etc. Intervals are named drop 4th = \4, uplift major 3rd = ^/M3, etc. Plain means neither up nor down nor lifted nor dropped. There may be upmid or liftmid intervals. Chords are named C-up add lift-seven = C^,/7 = C ^E G /Bb, C uplift-seven = C^/7 = C ^/E G ^/Bb, etc. See pergens.
Glossary / crash course
Over = prime in the numerator. Under = prime in the denominator. All = over, under or neither: wa = 3-limit, ya = 2.3.5, yaza = 2.3.5.7. Exponent = repeated syllable: triyo = yoyoyo = 125-over.
| prime | -o ("oh", /o̞/) for over | -u ("oo", /u/) for under | -a ("ah", /ä/) for all | -e ("eh", /ɛ/) for exponent | ||||
|---|---|---|---|---|---|---|---|---|
| 2 | — | — | (clear) | — | bi ("bee") | double | ||
| 3 | — | — | wa (white) | — | tri ("tree") | triple | ||
| quad | quadruple | |||||||
| 5 | yo (yellow) | y | gu (green) | g | ya | — | quin | quintuple |
| 7 | zo (azul) | z | ru (red) | r | za | — | sep | septuple |
| 11 | (i)lo | 1o | lu | 1u | (i)la | 1a | le | 11-fold |
| 13 | tho | 3o | thu | 3u | tha | 3a | the | 13-fold |
| 17 | (i)so | 17o | su | 17u | (i)sa | 17a | se | 17-fold |
| 19 | (i)no | 19o | (i)nu | 19u | na | 19a | ne | 19-fold |
| 23 | twetho | 23o | twethu | 23u | twetha | 23a | twethe | 23-fold |
Higher primes: 29o = tweno, 31o = thiwo, 37o = thiso, 41o = fowo, 43o = fotho, 47o = foso, 53o = fitho, 59o = fino, 61o = siwo, 67o = siso.
Exponents: sextuple is tribi (triply-doubled), octuple is quadbi, 9-fold is tritri, etc.
Pronunciation: exponent syllables like bi or tri are always unaccented. To emphasize the prime limit, the first occurrence of the highest prime is always accented: Biruyo, Bizozogu. In longer names, the 1st occurrence of sa/la and/or of lower primes may also be accented: Sasa-gugu, Zozotrigu.
| Word | Meaning | Example | |
|---|---|---|---|
| central | refers to a ratio centrally located in the lattice | every ratio of odd limit < 81 is central (but only some > 81 are not central) | |
| la- | L | large, augmented by 2187/2048 from the central ratio | 32/27 = wa 3rd = w3, 81/64 = lawa 3rd = Lw3 |
| sa- | s | small, diminished by 2187/2048 from the central ratio | 27/16 = wa 6th = w6, 128/81 = sawa 6th = sw6 |
| magnitude | refers to central, la, sa, lala, trisa, quadla, etc. | the sum of all prime exponents except the 1st, divided by 7 and rounded off | |
| i- | disambiguation prefix | no 3rd = omit the 3rd, but ino 3rd = 19/16 | |
| -a- | delimits an exponent such as bi-, tri-, etc. | Trizogu = 3zg = 1029/1000, but Trizo-agu = 3zag = 343/320 | |
| co- | c | compound (conventional term for widened by an 8ve) | 7/4 = zo 7th = z7, 7/2 = compound zo 7th = cozo 7th = cz7 |
| har | h | refers to a harmonic series (otonal) chord | 4:5:6:7 = C har-seven = Ch7 |
| sub | s | refers to a subharmonic series (utonal) chord | 7:6:5:4 = C sub-seven = Cs7 |
| po | p | adds a pythagorean comma, to change the degree | 15/14 = ruyo unison = ry1 = ruyopo 2nd = ryp2 |
| qu | q | subtracts a pythagorean comma | 49/48 = zozo 2nd = zz2 = zozoqu unison = zzq1 |
| -ti | T | changes a comma name to a temperament name | Gu = 81/80, Guti = meantone |
| -bi | #2 | as a suffix, 2nd smallest comma in the row segment | Guti = gT is Meantone, but Gubiti = g#2T is Father (16/15 vanishes) |
| Wa- | w- | alternate interval format, only used for 3-limit commas | Mercator's comma = Wa-53 = w-53 |
| nowa | remove 3 (wa) from the prime subgroup, i.e. no-threes | 2.5.7 = yaza nowa, 2.5.7 & 50/49 = Biruyoti nowa | |
| noca | remove 2 (clear) from the prime subgroup, i.e. non-8ve | 3.5.7 = yaza noca, 3.5.7 & 245/243 = Zozoyoti noca | |
| nowaca | remove both 2 and 3 from the prime subgroup | 5.7.11 = yazala nowaca | |
| plus | + | add an untempered prime to the temperament | Blackwood = 2.3.5 with 256/243 tempered out = Sawati + ya |
| and | & | joins commas that are tempered out | 7-limit Porcupine = 2.3.5.7 with 250/243 & 64/63 = Triyo & Ru |
| -ward | -wd | refers to the direction of chord root movement | Iy - IVy = 4thwd, Iy - Vy = 5thwd, Iy - yIIIy = yoward, Ig - gIIIg = guward |
Homonyms:
- "wa" means both "3-all" and "-one-all" (e.g. thiwa means 31-all). The meaning is always clear from context.
- "lo" means both "11-over" and "low", as in "low C". Thus 1o by itself becomes "ilo".
- "la" means both "11-all" and "large", and also the solfege note La. Thus 1a by itself becomes "ila".
- "so" means both "17-over" and the solfege note So. Thus 17o by itself becomes "iso".
- "sa" means both "17-all" and "small", and also the Saregam note Sa. Thus 17a by itself becomes "isa".
- "no" means both "19-over" and "omit", as in no3. Thus 19o by itself becomes "ino".
- "nu" means both "19-under" and "new", as in "the new key". Thus 19u by itself becomes "inu".
- "bi" means both "doubled" as in biruyo and "2nd smallest" as in Layobi. The meaning is always clear from context.
Temperaments use "virtual colors" represented with arrows ^ v and perhaps slashes / \
| Word | Meaning | |
|---|---|---|
| up | ^ | raised by some comma |
| down | v | lowered by some comma |
| arrow | refers collectively to both ups and downs | |
| lift | / | raised by some other comma |
| drop | \ | lowered by some other comma |
| slash | refers collectively to both lifts and drops | |
| inflection | refers collectively to both arrows and slashes | |
| alteration | refers collectively to both inflections and accidentals (sharps and flats) | |
| plain | ♢ | neither up nor down nor lifted nor dropped |
| mid | ~ | for 2nds, 3rd, 6ths and 7ths, exactly halfway between major and minor a mid 4th is halfway-augmented, and a mid 5th is halfway-diminished |
Translations
For translations of color notation terms into other languages, see Color notation/Translations. Translating avoids using sounds not in one's native language. For example, in many European languages, "th-" for prime 13 becomes "tr-".
Origins
Color notation was primarily developed by Kite Giedraitis, with much assistance from Praveen Venkataramana.
See also
- Kite's color notation/Catalog of rank-2 temperaments
- xen-calc – A web app that converts to/from ratios, prime-count vectors and color notation, and also supports ups and downs notation.
- ledzo notation – A similar competing notation system.
Further reading
- Giedraitis, Kite. Alternative Tunings: Theory, Notation and Practice.
| View • Talk • EditMusical notation | |
|---|---|
| Universal | Sagittal notation |
| Just intonation | Functional Just System • Ben Johnston's notation (Johnston–Copper notation) • Helmholtz–Ellis notation • Color notation |
| MOS scales | Diamond-mos notation • KISS notation (Quasi-diatonic MOS notation) |
| Temperaments | Circle-of-fifths notation • Ups and downs notation (alternative symbols) • Syntonic–rastmic subchroma notation • Extended meantone notation • Fractional sharp notation |
See musical notation for a longer list of systems by category. See Category:Notation for the most complete, comprehensive list, but not sorted by category. | |