Quasi-diatonic MOS notation
Quasi-diatonic MOS notation is a JI-agnostic notation system for MOS scales developed by CompactStar and VectorGraphics, which is designed as a natural extension of diatonic notation, instead of special-casing it as diamond-mos notation does. Alhough this specific notation was developed by them, several existing notations have similar concepts of extending diatonic notation logic to other MOSes, KISS notation, the melodic notations for antidiatonic, and the A–J notation for Bohlen–Pierce, the latter two of which were Vector's main inspiration. In diatonic, QDMN is identical to standard notation.
CompactStar considers it useful for diatonic-like scales, such as macro/microdiatonic scales, "long" diatonic scales, and antidiatonic.
There were originally two versions, the original version by CompactStar and Vector's version, but they were nearly identical so they were simply merged into one. Credit to CompactStar for the system for choosing the default mode, and for the specification of the MOS name at the top of the sheet music.
Note names
The root is A (A4), fixed to 440 Hz by default.
By default, starting from B, the notes of the darkest mode of the MOS are labelled until A an equave up (thanks CompactStar!), where the nominals repeat. So nominals in order are always A, B, C, D, E, F, G, etc. with the darkest mode being on B. For example, in 5L 3s, the darkest mode is sLsLLsLL, so the notes ABCDEFGH represent the scale LsLsLLsL on A. This is done to make it backwards-compatible with existing diatonic notation, which starts on B for its darkest mode, Locrian.
However, to enable compatibility with systems such as antidiatonic melodic notation and Bohlen–Pierce notation, the mode on A used for nominals can be explicitly specified. More info in the Staves section.
I is skipped, as in Bohlen–Pierce, to avoid confusion, and V is skipped as well.
Note that this is incompatible with conventional Bohlen–Pierce notation itself, as it refers to BP's note "C" as A, though this can be fixed by explicitly specifying a mode.
Accidentals are ♯ and ♭, which raise and lower by a chroma (the difference between a large and small step, L − s) respectively. Double sharp and double flat work as expected.
So, in 13edo, the notes of 5L 3s are:
A, A♯/B♭, B, C, C♯/D♭, D, E, E♯/F♭, F, F♯/G♭, G, H, H♯/A♭, and A an octave higher.
MODMOSes are notated using the MOS's base notation.
Interval names
Intervals are named analogously to diatonic: interval size classes are named with ordinal numbers starting from the scale step as the 2nd (i.e. they are 1-indexed). So a 2-step would be a third, a 3-step would be a fourth, etc. The exceptions are the 0-step (which is called the unison), and the equave (which is named after an Anglicized version of the Latin ordinal for the interval). A table of equave names will be available at the bottom of the page). (Note that these are not true Latin ordinals, unlike the corresponding Italian notation of ottava (see staff notation).)
Generators are perfect, other intervals are major and minor (where major refers to the larger of the two interval sizes, and minor refers to the smaller of the two). Augmented and diminished, for interval names, function as ♯ and ♭ do for note names respectively. So in 5L 3s (and in fact, in any MOS with > 3 notes and no consecutive small steps that is not an edo, due to the way the position of A in the scale is defined), A–C is a minor third, A–C♯ is a major third, and A–C𝄪 is an augmented third. Augmented and diminished are also used to name the 1 imperfect generator interval of each class, depending on its size relative to the perfect generator. As such, in 5L 3s, there are 7 perfect sixths and one augmented sixth.
Interval classes may be distinguished using TAMNAMS MOS prefixes. For example, the generator of armotonic might be called an armsixth to reduce ambiguity.
Staves
The number of staff lines is equal to half the number of scale steps plus 1 (rounding up). So a scale with 8 notes would have 5 lines, a scale with 9 notes would have 6 lines, and a scale of 11 notes would have 7 lines. A3 is always on a staff line.
The MOS name is always written at the top of the sheet music, along with the mode on A used for nominals, if that differs from the default.
New clefs need to be introduced to refer to arbitrary notes, in order to bridge the gap between the A clef (introduced specifically for this notation) and the C, F, and G clefs (shared with diatonic), and allow for the convenient and analogous notation of a scale with any number of notes.
A clef refers to the closest note on a staff line with that name to A3 (an equave below A4). For example, in diatonic, the G clef refers to the G above middle C, because that's the closest G staff line to A3. Similarly, the F clef refers to the F below middle C, because that's the closest F staff line to A3.(So of course, a clef is only valid where such a staff line exists, i.e. in an octatonic scale where all the staff lines are A, C, E, and G, an F clef would not be valid. A J clef would also not be valid, because there is no note named J.)
You may choose clefs based on the system provided in the next section, or, by CompactStar's preference, using only the C, G, and F clefs, and the nonstandard A clef if necessary (i.e. in 1L 1s).
Additionally, if two of the same note on a staff line are equally close to A3, such as with an E clef in an octatonic scale, it refers to the note above A3.

The MOS is always specified with text above the beginning of the score (for example, "oneirotonic", "5L 3s", or "LLsLLsLs").
8va markings work as normal, though the number is changed to match the number of steps in the equave, i.e. 9na for oneirotonic, or 10ma for gramitonic. It is read as the Italian ordinal for the given number, and the last two letters also come from that (with the ending changed to -a if necessary). (This follows from the use of 15ma in Western music.) It can be called an equava in general.
Key signatures are notated as you would expect given the principle of generalizing from diatonic.
Tables and other resources
Equave names
A table of what the equave is called based on how many steps it contains. This is distinct from the Greek numbers used to name harmonics, as the term "octave" comes from Latin. The -us ending is dropped from Latin numerals (as in second and quart) except where a final silent -e is kept to indicate a long vowel (as in octave), except where said -e would lead to confusion (as with non, where it would be confused with "none", also, the English pronunciation of the Latin non- root does not include a long vowel)
| Steps (1-indexed) | Name | Equava marking |
|---|---|---|
| 2 | Second | 2da "seconda" |
| 3 | Terce | 3za "terza" |
| 4 | Quart | 4ta "quarta" |
| 5 | Quint | 5ta "quinta" |
| 6 | Sext | 6ta "sesta" |
| 7 | Septim | 7ma "settima" |
| 8 | Octave | 8va "ottava" |
| 9 | Non | 9na "nona" |
| 10 | Decim | 10ma "decima" |
| 11 | Undecim | 11ma "undicesima" |
| 12 | Duodecim | 12ma "dodicesima" |
| 13 | Tertiodecim | 13ma "tredicesima" |
| 14 | Quartodecim | 14ma "quattordicesima" |
| 15 | Quintodecim | 15ma "quindicesima" |
| 16 | Sextodecim | 16ma "sedicesima" |
| 17 | Septimodecim | 17ma "diciassettesima" |
| 18 | Duodevicesim | 18ma "diciottesima" |
| 19 | Undevicesim | 19ma "diciannovesima" |
| 20 | Vicesim | 20ma "ventesima" |
| 21 | Vicesimoprime | 21ma "ventunesima" |
| 22 | Vicesimosecond | 22ma "ventiduesima" |
| 23 | Vicesimoterce | 23ma "ventitreesima" |
| 24 | Vicesimoquart | 24ma "ventiquattresima" |
| 25 | Vicesimoquint | 25ma "venticinquesima" |
Optimal clefs
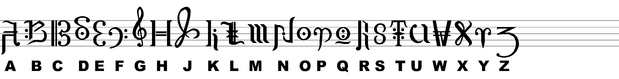
This is the table of optimal clef layouts to be analogous to the treble and bass clef for scales with different sizes. This assumes that A3 is the top line of the bass clef. Preferably, the second line from the bottom of the staff is used as the treble clef, and the second line from the top is used as the bass clef, except when that would cause a clef with an equave up/down which could be avoided by using a different line for the clef indicator.
| Scale size | Staff lines | Treble clef | Bass clef |
|---|---|---|---|
| 3 | 3 | A (quarta up) on 2nd line | B on 2nd line |
| 4 | 3 | A (quinta up) on 1st line | A on 3rd line |
| 5 | 4 | E on 1st line | D on 3rd line |
| 6 | 4 | A (settima up) on 2nd line | E on 3rd line |
| 7 | 5 | G on 2nd line | F on 4th line |
| 8 | 5 | E on 1st line | G on 4th line |
| 9 | 6 | G on 2nd line | H on 5th line |
| 10 | 6 | E on 1st line | J on 5th line |
| 11 | 7 | G on 2nd line | K on 6th line |
| 12 | 7 | L on 6th line | |
| 13 | 8 | M on 7th line | |
| 14 | 8 | N on 7th line | |
| 15 | 9 | O on 8th line | |
| 16 | 9 | P on 8th line | |
| 17 | 10 | Q on 9th line | |
| 18 | 10 | R on 9th line | |
| 19 | 11 | S on 10th line | |
| 20 | 11 | T on 10th line |
Extension to other scales

For ternary systems, sharps and flats can be given subscripts or superscripts indicating what diesis is being sharpened or flattened by (ᴸᵐ, ᵐˢ). In notation,, these are written in small text above or below the accidental. When there are two sets of accidentals, the smaller chroma may be written as an arrow.
Examples
Pentic
| Interval | Steps subtended | Note name (from A = unison) | Soft tuning |
|---|---|---|---|
| perfect unison | — | A | 0 ¢ |
| minor second | s | Bb | 200 ¢ |
| major second | L | B | 300 ¢ |
| diminished third | 2s | Cb | 400 ¢ |
| perfect third | L + s | C | 500 ¢ |
| perfect fourth | L + 2s | D | 700 ¢ |
| augmented fourth | 2L + s | D# | 800 ¢ |
| minor fifth | 1L + 3s | Eb | 900 ¢ |
| major fifth | 2L + 2s | E | 1000 ¢ |
| perfect sext | 2L + 3s | A | 1200 ¢ |
Oneirotonic
| Interval | Steps subtended | Note name (from A = unison) | Soft tuning |
|---|---|---|---|
| perfect unison | — | A | 0 ¢ |
| minor second | s | Bb | 114.29 ¢ |
| major second | L | B | 171.43 ¢ |
| minor third | L + s | C | 285.71 ¢ |
| major third | 2L | C# | 342.86 ¢ |
| diminished fourth | L + 2s | Db | 400.00 ¢ |
| perfect fourth | 2L + s | D | 457.14 ¢ |
| minor fifth | 2L + 2s | E | 571.43 ¢ |
| major fifth | 3L + s | E# | 628.57 ¢ |
| perfect sixth | 3L + 2s | F | 742.86 ¢ |
| augmented sixth | 4L + s | F# | 800.00 ¢ |
| minor seventh | 3L + 3s | Gb | 857.14 ¢ |
| major seventh | 4L + 2s | G | 914.29 ¢ |
| minor eighth | 4L + 3s | H | 1028.57 ¢ |
| major eighth | 5L + 2s | H# | 1085.71 ¢ |
| perfect non | 5L + 3s | A | 1200 ¢ |
Compatibility with German and fixed-do systems
German H system
As each interval in a MOS has one of two values, the note in the expected place of B is labelled H; the note that is the other size of second above A is labelled B. This note should usually be English B flat, as the last interval of the darkest mode of any MOS is always an L step. For notating edos as degenerate MOSes, the note name B is preferred over H, but H is still skipped after G. For scales with more than two sizes of second, the note a second above A that is furthest from H is labelled B. This means the German H system is only compatible with 23 notes, as opposed to the English system's 24.
Fixed do
Solfege follows a simple pattern, starts from the note two steps above A (this is "C" in scales with more than 2 pitch classes) and stops at the note before the next A, which is labeled "sol", then "la" and "si". The consonants chosen have been selected to be compatible with the phonology of many languages, and follow a cycle of 9 while the vowels follow a cycle of 5.
The vowels are the five-vowel system, the pronunciation of each consonant is as follows:
| Consonant | IPA value | English example |
|---|---|---|
| d | /d/ | door |
| r | /r/ | water[note 1] |
| m | /m/ | man |
| f | /f/ | fine |
| k | /k/ | car |
| b | /b/ | best |
| n | /n/ | north |
| g | /g/ | gate |
| t | /t/ | tell |
| s | /s/ | see |
| l | /l/ | law[note 2] |
| Alphabetic | German H | Solfege consonant | Solfege vowel | Full solfege |
|---|---|---|---|---|
| C | C | d | o | do |
| D | D | r | e | re |
| E | E | m | i | mi |
| F | F | f | a | fa |
| G | G | k | u | ku |
| H | J | b | o | bo |
| J | K | n | e | ne |
| K | L | g | i | gi |
| L | M | t | a | ta |
| M | N | d | u | du |
| N | O | r | o | ro |
| O | P | m | e | me |
| P | Q | f | i | fi |
| Q | R | k | a | ka |
| R | S | b | u | bu |
| S | T | n | o | no |
| T | U | g | e | ge |
| U | W | t | i | te[note 3] |
| W | X | d | a | da |
| X | Y | r | u | ru |
| Y | Z | m | o | mo |
| (Last note) | (Last note) | - | - | sol |
| A | A | - | - | la |
| B flat | B | - | - | si bemol |
| B | H | - | - | si |
Notes
| View • Talk • EditMusical notation | |
|---|---|
| Universal | Sagittal notation |
| Just intonation | Functional Just System • Ben Johnston's notation (Johnston–Copper notation) • Helmholtz–Ellis notation • Color notation |
| MOS scales | Diamond-mos notation • KISS notation (Quasi-diatonic MOS notation) |
| Temperaments | Circle-of-fifths notation • Ups and downs notation (alternative symbols) • Syntonic–rastmic subchroma notation • Extended meantone notation • Fractional sharp notation |
See musical notation for a longer list of systems by category. See Category:Notation for the most complete, comprehensive list, but not sorted by category. | |