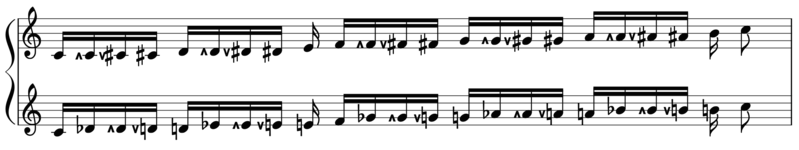22edo: Difference between revisions
Fixed link Tags: Visual edit Mobile edit Mobile web edit Advanced mobile edit |
m Restore wiki formatting Tag: Undo |
||
| Line 14: | Line 14: | ||
=== Overview to JI approximation quality === | === Overview to JI approximation quality === | ||
The 22edo system is in fact the third equal division, after 12 and 19, which is capable of approximating the [[5-limit]] to within a [[Tenney- | The 22edo system is in fact the third equal division, after 12 and 19, which is capable of approximating the [[5-limit]] to within a [[Tenney-Euclidean temperament measures #TE error|Tenney–Euclidean error]] of 4 cents per octave. While not an [[zeta integral edo|integral]] or [[zeta gap edo|gap edo]] it at least qualifies as a [[zeta peak edo|zeta peak]]. Moreover, there is more to it than just the 5-limit; unlike 12 or 19, it is able to approximate the [[7-limit|7-]] and [[11-limit]] to within 3 cents/oct of error. While [[31edo]] does much better, 22edo still allows the use of these higher-limit harmonies, and in fact 22 is the smallest equal division of the octave to represent the [[11-odd-limit]] [[consistent|consistently]]. Furthermore, 22edo, unlike 12 and 19, is not a [[meantone]] system. The net effect is that 22 allows, and to some extent even forces, the exploration of less familiar musical territory, yet is small enough that it can be used in live performances with suitably designed instruments, like 22-tone guitars. | ||
22edo can also be treated as adding harmonics 3 and 5 to [[11edo]]'s 2.9.15.7.11.17 subgroup, making it a rather accurate 2.3.5.7.11.17 [[subgroup]] temperament. Let us also mind its approximation of the 31st harmonic is within half a cent, which is very accurate. It also approximates some intervals involving the 29th harmonic well, especially 29/24, which is also matched within half a cent. This leaves us with 2.3.5.7.11.17.29.31. | 22edo can also be treated as adding harmonics 3 and 5 to [[11edo]]'s 2.9.15.7.11.17 subgroup, making it a rather accurate 2.3.5.7.11.17 [[subgroup]] temperament. Let us also mind its approximation of the 31st harmonic is within half a cent, which is very accurate. It also approximates some intervals involving the 29th harmonic well, especially 29/24, which is also matched within half a cent. This leaves us with 2.3.5.7.11.17.29.31. | ||
| Line 22: | Line 22: | ||
22edo is also the third-smallest edo (after [[10edo]] and [[15edo]]) that maintains [[minimal consistent EDOs|25% or lower relative error]] on all of the first eight harmonics of the [[harmonic series]]. | 22edo is also the third-smallest edo (after [[10edo]] and [[15edo]]) that maintains [[minimal consistent EDOs|25% or lower relative error]] on all of the first eight harmonics of the [[harmonic series]]. | ||
===Prime harmonics=== | === Prime harmonics === | ||
{{Harmonics in equal|22|columns=11}} | {{Harmonics in equal|22|columns=11}} | ||
===Subsets and supersets=== | === Subsets and supersets === | ||
As 22 is divisible by 11, a 22edo instrument can play any music in 11edo, in the same way that [[12edo]] can play [[6edo]] (the whole tone scale). 11edo is interesting for sounding melodically very similar to 12edo (whole steps, half steps and minor thirds in the familiar 1:2:3 ratio), but harmonically very different, in particular because it lacks perfect fifths/fourths and 5-limit major thirds/minor sixths. Similarly, 22edo is melodically similar to [[24edo]] as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In [[Sagittal notation]], 11 can be notated as every other note of 22. | As 22 is divisible by 11, a 22edo instrument can play any music in 11edo, in the same way that [[12edo]] can play [[6edo]] (the whole tone scale). 11edo is interesting for sounding melodically very similar to 12edo (whole steps, half steps and minor thirds in the familiar 1:2:3 ratio), but harmonically very different, in particular because it lacks perfect fifths/fourths and 5-limit major thirds/minor sixths. Similarly, 22edo is melodically similar to [[24edo]] as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In [[Sagittal notation]], 11 can be notated as every other note of 22. | ||
==Intervals== | == Intervals == | ||
{{See also|22edo solfege}} | {{See also|22edo solfege}} | ||
{{See also|SKULO interval names#Alternatives}} | {{See also|SKULO interval names#Alternatives}} | ||
| Line 34: | Line 34: | ||
{| class="wikitable center-all right-2 left-3" | {| class="wikitable center-all right-2 left-3" | ||
|- | |- | ||
!Degree | ! Degree | ||
!Cents | ! Cents | ||
!Approximate Ratios<ref group="note">{{sg|limit=2.3.5.7.11.17 subgroup}}</ref> | ! Approximate Ratios<ref group="note">{{sg|limit=2.3.5.7.11.17 subgroup}}</ref> | ||
! colspan="3" |[[Ups and Downs Notation|Ups and downs notation]]<br>([[Enharmonic unisons in ups and downs notation|EUs]]: v<sup>3</sup>A1 and ^^d2) | ! colspan="3" | [[Ups and Downs Notation|Ups and downs notation]]<br>([[Enharmonic unisons in ups and downs notation|EUs]]: v<sup>3</sup>A1 and ^^d2) | ||
! colspan="3" |[[SKULO interval names|SKULO notation]] {{nowrap|(K {{=}} 1)}} | ! colspan="3" | [[SKULO interval names|SKULO notation]] {{nowrap|(K {{=}} 1)}} | ||
!Audio | ! Audio | ||
|- | |- | ||
|0 | | 0 | ||
|0.0 | | 0.0 | ||
|[[1/1]] | | [[1/1]] | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
| [[File:0-0.000c_P1.mp3]] | | [[File:0-0.000c_P1.mp3]] | ||
|- | |- | ||
|1 | | 1 | ||
|54.5 | | 54.5 | ||
|[[36/35]], [[34/33]], [[33/32]], [[32/31]] | | [[36/35]], [[34/33]], [[33/32]], [[32/31]] | ||
| up-unison, minor 2nd | | up-unison, minor 2nd | ||
|^1, m2 | | ^1, m2 | ||
|^D, Eb | | ^D, Eb | ||
|comma-wide unison, minor 2nd | | comma-wide unison, minor 2nd | ||
|K1, m2 | | K1, m2 | ||
|KD, Eb | | KD, Eb | ||
|[[File:0-54.545c_22edo.mp3]] | | [[File:0-54.545c_22edo.mp3]] | ||
|- | |- | ||
|2 | | 2 | ||
| 109.1 | | 109.1 | ||
|[[18/17]], [[17/16]], [[16/15]], [[15/14]] | | [[18/17]], [[17/16]], [[16/15]], [[15/14]] | ||
|downaug 1sn, upminor 2nd | | downaug 1sn, upminor 2nd | ||
|vA1, ^m2 | | vA1, ^m2 | ||
|vD#, ^Eb | | vD#, ^Eb | ||
|classic minor 2nd | | classic minor 2nd | ||
|Km2 | | Km2 | ||
| KEb | | KEb | ||
|[[File:0-109.091c_11edo.mp3]] | | [[File:0-109.091c_11edo.mp3]] | ||
|- | |- | ||
|3 | | 3 | ||
| 163.6 | | 163.6 | ||
|[[12/11]], [[11/10]], [[10/9]] | | [[12/11]], [[11/10]], [[10/9]] | ||
|aug 1sn, downmajor 2nd | | aug 1sn, downmajor 2nd | ||
|A1, vM2 | | A1, vM2 | ||
|D#, vE | | D#, vE | ||
|classic/comma-narrow major 2nd | | classic/comma-narrow major 2nd | ||
|kM2 | | kM2 | ||
|kE | | kE | ||
|[[File:0-163.636c_22edo.mp3]] | | [[File:0-163.636c_22edo.mp3]] | ||
|- | |- | ||
|4 | | 4 | ||
|218.2 | | 218.2 | ||
|[[9/8]], [[17/15]], [[8/7]] | | [[9/8]], [[17/15]], [[8/7]] | ||
|major 2nd | | major 2nd | ||
|M2 | | M2 | ||
|E | | E | ||
|major 2nd | | major 2nd | ||
|M2 | | M2 | ||
|E | | E | ||
|[[File:0-218.182c_11edo.mp3]] | | [[File:0-218.182c_11edo.mp3]] | ||
|- | |- | ||
|5 | | 5 | ||
| 272.7 | | 272.7 | ||
|[[20/17]], [[7/6]] | | [[20/17]], [[7/6]] | ||
|minor 3rd | | minor 3rd | ||
|m3 | | m3 | ||
|F | | F | ||
|minor 3rd | | minor 3rd | ||
|m3 | | m3 | ||
|F | | F | ||
|[[File:0-272.727c_22edo.mp3]] | | [[File:0-272.727c_22edo.mp3]] | ||
|- | |- | ||
|6 | | 6 | ||
|327.3 | | 327.3 | ||
|[[6/5]], [[17/14]], [[11/9]] | | [[6/5]], [[17/14]], [[11/9]] | ||
|upminor 3rd | | upminor 3rd | ||
|^m3 | | ^m3 | ||
|^F | | ^F | ||
|classic minor 3rd | | classic minor 3rd | ||
|Km3 | | Km3 | ||
|KF | | KF | ||
|[[File:0-327.273c_11edo.mp3]] | | [[File:0-327.273c_11edo.mp3]] | ||
|- | |- | ||
|7 | | 7 | ||
|381.8 | | 381.8 | ||
| | | [[5/4]], [[96/77]] | ||
[[5/4]], [[96/77]] | | downmajor 3rd | ||
|downmajor 3rd | | vM3 | ||
|vM3 | | vF# | ||
|vF# | | classic major 3rd | ||
|classic major 3rd | | kM3 | ||
|kM3 | |||
| kF# | | kF# | ||
|[[File:0-381.818c_22edo.mp3]] | | [[File:0-381.818c_22edo.mp3]] | ||
|- | |- | ||
|8 | | 8 | ||
|436.4 | | 436.4 | ||
|[[14/11]], [[9/7]], [[22/17]] | | [[14/11]], [[9/7]], [[22/17]] | ||
|major 3rd | | major 3rd | ||
|M3 | | M3 | ||
|F# | | F# | ||
|major 3rd | | major 3rd | ||
|M3 | | M3 | ||
|F# | | F# | ||
|[[File:0-436.364c_11edo.mp3]] | | [[File:0-436.364c_11edo.mp3]] | ||
|- | |- | ||
| 9 | | 9 | ||
| 490.9 | | 490.9 | ||
| [[4/3]] | | [[4/3]] | ||
|perfect 4th | | perfect 4th | ||
|P4 | | P4 | ||
|G | | G | ||
|perfect 4th | | perfect 4th | ||
|P4 | | P4 | ||
|G | | G | ||
|[[File:0-490.909c_22edo.mp3]] | | [[File:0-490.909c_22edo.mp3]] | ||
|- | |- | ||
|10 | | 10 | ||
|545.5 | | 545.5 | ||
|[[15/11]], [[11/8]] | | [[15/11]], [[11/8]] | ||
|up-4th, dim 5th | | up-4th, dim 5th | ||
|^4, d5 | | ^4, d5 | ||
|^G, Ab | | ^G, Ab | ||
|comma-wide 4th | | comma-wide 4th | ||
|K4 | | K4 | ||
|KG | | KG | ||
|[[File:0-545.455c_11edo.mp3]] | | [[File:0-545.455c_11edo.mp3]] | ||
|- | |- | ||
|11 | | 11 | ||
|600.0 | | 600.0 | ||
|[[7/5]], [[24/17]], [[17/12]], [[10/7]] | | [[7/5]], [[24/17]], [[17/12]], [[10/7]] | ||
| downaug 4th, updim 5th | | downaug 4th, updim 5th | ||
|vA4, ^d5 | | vA4, ^d5 | ||
| vG#, ^Ab | | vG#, ^Ab | ||
|comma-narrow augmented 4th<br />comma-wide diminished 5th | | comma-narrow augmented 4th<br />comma-wide diminished 5th | ||
|kA4<br />Kd5 | | kA4<br />Kd5 | ||
|kG#, KAb | | kG#, KAb | ||
|[[File:0-600.000c_2edo.mp3]] | | [[File:0-600.000c_2edo.mp3]] | ||
|- | |- | ||
|12 | | 12 | ||
|654.5 | | 654.5 | ||
| | | [[16/11]], [[22/15]] | ||
[[16/11]], [[22/15]] | | aug 4th, down-5th | ||
|aug 4th, down-5th | | A4, v5 | ||
|A4, v5 | | G#, vA | ||
|G#, vA | | comma-narrow 5th | ||
|comma-narrow 5th | | k5 | ||
|k5 | | kA | ||
|kA | | [[File:0-654.545c_11edo.mp3]] | ||
|[[File:0-654.545c_11edo.mp3]] | |||
|- | |- | ||
|13 | | 13 | ||
| 709.1 | | 709.1 | ||
| [[3/2]] | | [[3/2]] | ||
|perfect 5th | | perfect 5th | ||
|P5 | | P5 | ||
|A | | A | ||
|perfect 5th | | perfect 5th | ||
|P5 | | P5 | ||
|A | | A | ||
|[[File:0-709.091c_22edo.mp3]] | | [[File:0-709.091c_22edo.mp3]] | ||
|- | |- | ||
|14 | | 14 | ||
|763.6 | | 763.6 | ||
|[[17/11]], [[14/9]], [[11/7]] | | [[17/11]], [[14/9]], [[11/7]] | ||
|minor 6th | | minor 6th | ||
|m6 | | m6 | ||
|Bb | | Bb | ||
|minor 6th | | minor 6th | ||
|m6 | | m6 | ||
|Bb | | Bb | ||
|[[File:0-763.636c_11edo.mp3]] | | [[File:0-763.636c_11edo.mp3]] | ||
|- | |- | ||
|15 | | 15 | ||
|818.2 | | 818.2 | ||
| [[8/5]], [[77/48]] | | [[8/5]], [[77/48]] | ||
|upminor 6th | | upminor 6th | ||
|^m6 | | ^m6 | ||
|^Bb | | ^Bb | ||
|classic minor 6th | | classic minor 6th | ||
|Km6 | | Km6 | ||
| KBb | | KBb | ||
|[[File:0-818.182c_22edo.mp3]] | | [[File:0-818.182c_22edo.mp3]] | ||
|- | |- | ||
|16 | | 16 | ||
|872.7 | | 872.7 | ||
|[[18/11]], [[28/17]], [[5/3]] | | [[18/11]], [[28/17]], [[5/3]] | ||
| downmajor 6th | | downmajor 6th | ||
|vM6 | | vM6 | ||
|vB | | vB | ||
|classic major 6th | | classic major 6th | ||
|kM6 | | kM6 | ||
|kB | | kB | ||
|[[File:0-872.727c_11edo.mp3]] | | [[File:0-872.727c_11edo.mp3]] | ||
|- | |- | ||
| 17 | | 17 | ||
|927.3 | | 927.3 | ||
| | | [[17/10]], [[12/7]] | ||
[[17/10]], [[12/7]] | | major 6th | ||
|major 6th | | M6 | ||
|M6 | | B | ||
|B | | major 6th | ||
|major 6th | | M6 | ||
|M6 | | B | ||
|B | | [[File:0-927.273c_22edo.mp3]] | ||
|[[File:0-927.273c_22edo.mp3]] | |||
|- | |- | ||
|18 | | 18 | ||
|981.8 | | 981.8 | ||
| | | [[7/4]], [[30/17]], [[16/9]] | ||
[[7/4]], [[30/17]], [[16/9]] | | minor 7th | ||
|minor 7th | | m7 | ||
|m7 | | C | ||
|C | | minor 7th | ||
|minor 7th | | m7 | ||
|m7 | | C | ||
|C | | [[File:0-981.818c_11edo.mp3]] | ||
|[[File:0-981.818c_11edo.mp3]] | |||
|- | |- | ||
|19 | | 19 | ||
|1036.4 | | 1036.4 | ||
|[[9/5]], [[11/6]], [[20/11]] | | [[9/5]], [[11/6]], [[20/11]] | ||
|upminor 7th, dim 8ve | | upminor 7th, dim 8ve | ||
|^m7, d8 | | ^m7, d8 | ||
|^C, Db | | ^C, Db | ||
|classic minor 7th | | classic minor 7th | ||
|Km7 | | Km7 | ||
| kC | | kC | ||
| [[File:0-1036.364c_22edo.mp3]] | | [[File:0-1036.364c_22edo.mp3]] | ||
|- | |- | ||
|20 | | 20 | ||
| 1090.9 | | 1090.9 | ||
| | | [[28/15]], [[15/8]], [[32/17]], [[17/9]] | ||
[[28/15]], [[15/8]], [[32/17]], [[17/9]] | | downmajor 7th, updim 8ve | ||
|downmajor 7th, updim 8ve | | vM7, ^d8 | ||
|vM7, ^d8 | | vC#, ^Db | ||
|vC#, ^Db | | classic major 7th | ||
|classic major 7th | | kM7 | ||
|kM7 | | kC# | ||
|kC# | |||
| [[File:0-1090.909c_11edo.mp3]] | | [[File:0-1090.909c_11edo.mp3]] | ||
|- | |- | ||
|21 | | 21 | ||
|1145.5 | | 1145.5 | ||
|[[31/16]], [[64/33]], [[33/17]], [[35/18]] | | [[31/16]], [[64/33]], [[33/17]], [[35/18]] | ||
|major 7th, down 8ve | | major 7th, down 8ve | ||
|M7, v8 | | M7, v8 | ||
|C#, vD | | C#, vD | ||
| major 7th / comma-narrow 8ve | | major 7th / comma-narrow 8ve | ||
|M7 / k8 | | M7 / k8 | ||
|C#, kD | | C#, kD | ||
| [[File:0-1145.455c_22edo.mp3]] | | [[File:0-1145.455c_22edo.mp3]] | ||
|- | |- | ||
| 22 | | 22 | ||
| 1200.0 | | 1200.0 | ||
|[[2/1]] | | [[2/1]] | ||
|perfect octave | | perfect octave | ||
|P8 | | P8 | ||
|D | | D | ||
|perfect 8ve | | perfect 8ve | ||
|P8 | | P8 | ||
|D | | D | ||
|[[File:0-1200.000c_P8.mp3]] | | [[File:0-1200.000c_P8.mp3]] | ||
|} | |} | ||
==Notation == | == Notation == | ||
=== Ups and downs notation=== | === Ups and downs notation === | ||
Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud. | Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud. | ||
{{sharpness-sharp3a}} | {{sharpness-sharp3a}} | ||
| Line 308: | Line 303: | ||
{| class="wikitable right-1 right-2 center-3 center-4" | {| class="wikitable right-1 right-2 center-3 center-4" | ||
|+ style="font-size: 105%;" |Notation of 22edo | |+ style="font-size: 105%;" | Notation of 22edo | ||
|- | |- | ||
! rowspan="2" |[[Degree]] | ! rowspan="2" | [[Degree]] | ||
! rowspan="2" |[[Cent]]s | ! rowspan="2" | [[Cent]]s | ||
! colspan="2" |[[Ups and downs notation|Ups and Downs Notation]] | ! colspan="2" | [[Ups and downs notation|Ups and Downs Notation]] | ||
|- | |- | ||
! [[5L 2s|Diatonic Interval Names]] | ! [[5L 2s|Diatonic Interval Names]] | ||
!Note Names | ! Note Names | ||
|- | |- | ||
|0 | | 0 | ||
|0.0 | | 0.0 | ||
| '''Perfect unison (P1)''' | | '''Perfect unison (P1)''' | ||
|'''D''' | | '''D''' | ||
|- | |- | ||
|1 | | 1 | ||
|54.5 | | 54.5 | ||
|Minor second (m2)<br />Up unison (^1) | | Minor second (m2)<br />Up unison (^1) | ||
|Eb<br />^D | | Eb<br />^D | ||
|- | |- | ||
|2 | | 2 | ||
|109.1 | | 109.1 | ||
|Upminor second (^m2)<br />Downaugmented unison (vA1)<br />Diminished third (d3) | | Upminor second (^m2)<br />Downaugmented unison (vA1)<br />Diminished third (d3) | ||
|^Eb<br />vD#<br />Fb | | ^Eb<br />vD#<br />Fb | ||
|- | |- | ||
|3 | | 3 | ||
|163.6 | | 163.6 | ||
|Downmajor second (vM2)<br />Augmented unison (A1) | | Downmajor second (vM2)<br />Augmented unison (A1) | ||
|vE<br />D# | | vE<br />D# | ||
|- | |- | ||
|4 | | 4 | ||
|218.2 | | 218.2 | ||
| '''Major second (M2)'''<br />Upaugmented unison (^A1)<br />Downminor third (vm3) | | '''Major second (M2)'''<br />Upaugmented unison (^A1)<br />Downminor third (vm3) | ||
|'''E'''<br />^D#<br />vF | | '''E'''<br />^D#<br />vF | ||
|- | |- | ||
|5 | | 5 | ||
|272.7 | | 272.7 | ||
| Upmajor second (^M2)<br />'''Minor third (m3)''' | | Upmajor second (^M2)<br />'''Minor third (m3)''' | ||
|^E<br />'''F''' | | ^E<br />'''F''' | ||
|- | |- | ||
| 6 | | 6 | ||
|327.3 | | 327.3 | ||
|'''Upminor third (^m3)'''<br />Diminished fourth (d4) | | '''Upminor third (^m3)'''<br />Diminished fourth (d4) | ||
|'''^F'''<br />Gb | | '''^F'''<br />Gb | ||
|- | |- | ||
|7 | | 7 | ||
|381.8 | | 381.8 | ||
|'''Downmajor third (vM3)'''<br />Augmented second (A2)<br />Updiminished fourth (^d4) | | '''Downmajor third (vM3)'''<br />Augmented second (A2)<br />Updiminished fourth (^d4) | ||
|'''vF#'''<br />E#<br />^Gb | | '''vF#'''<br />E#<br />^Gb | ||
|- | |- | ||
|8 | | 8 | ||
|436.4 | | 436.4 | ||
|'''Major third (M3)'''<br />Upaugmented second (^A2)<br />Down fourth (v4) | | '''Major third (M3)'''<br />Upaugmented second (^A2)<br />Down fourth (v4) | ||
| | | '''F#'''<br />^E#<br />vG | ||
'''F#'''<br />^E#<br />vG | |||
|- | |- | ||
|9 | | 9 | ||
|490.9 | | 490.9 | ||
| '''Perfect fourth (P4)''' | | '''Perfect fourth (P4)''' | ||
|'''G''' | | '''G''' | ||
|- | |- | ||
|10 | | 10 | ||
|545.5 | | 545.5 | ||
|Up fourth (^4)<br />Diminished fifth (d5) | | Up fourth (^4)<br />Diminished fifth (d5) | ||
|^G<br />Ab | | ^G<br />Ab | ||
|- | |- | ||
|11 | | 11 | ||
|600.0 | | 600.0 | ||
|Downaugmented fourth (vA4)<br />Updiminished fifth (^d5) | | Downaugmented fourth (vA4)<br />Updiminished fifth (^d5) | ||
| vG#<br />^Ab | | vG#<br />^Ab | ||
|- | |- | ||
|12 | | 12 | ||
|654.5 | | 654.5 | ||
|Augmented fourth (A4)<br />Down fifth (v5) | | Augmented fourth (A4)<br />Down fifth (v5) | ||
|G#<br />vA | | G#<br />vA | ||
|- | |- | ||
|13 | | 13 | ||
|709.1 | | 709.1 | ||
|'''Perfect fifth (P5)''' | | '''Perfect fifth (P5)''' | ||
|'''A''' | | '''A''' | ||
|- | |- | ||
|14 | | 14 | ||
|763.6 | | 763.6 | ||
|Up fifth (^5)<br />Minor sixth (m6) | | Up fifth (^5)<br />Minor sixth (m6) | ||
|^A<br />Bb | | ^A<br />Bb | ||
|- | |- | ||
|15 | | 15 | ||
|818.2 | | 818.2 | ||
|Downaugmented fifth (vA5)<br />Upminor sixth (^m6) | | Downaugmented fifth (vA5)<br />Upminor sixth (^m6) | ||
| vA#<br />^Bb | | vA#<br />^Bb | ||
|- | |- | ||
|16 | | 16 | ||
|872.7 | | 872.7 | ||
|Augmented fifth (A5)<br />'''Downmajor sixth (vM6)''' | | Augmented fifth (A5)<br />'''Downmajor sixth (vM6)''' | ||
|A#<br />'''vB''' | | A#<br />'''vB''' | ||
|- | |- | ||
|17 | | 17 | ||
|927.3 | | 927.3 | ||
|'''Major sixth (M6)'''<br />Upaugmented fifth (^A5)<br />Downminor seventh (vm7) | | '''Major sixth (M6)'''<br />Upaugmented fifth (^A5)<br />Downminor seventh (vm7) | ||
| | | '''B'''<br />^A#<br />vC | ||
'''B'''<br />^A#<br />vC | |||
|- | |- | ||
| 18 | | 18 | ||
|981.8 | | 981.8 | ||
|'''Minor seventh (m7)'''<br />Upmajor sixth (^M6)<br />Downdiminished octave (vd8) | | '''Minor seventh (m7)'''<br />Upmajor sixth (^M6)<br />Downdiminished octave (vd8) | ||
|'''C'''<br />^B<br />vDb | | '''C'''<br />^B<br />vDb | ||
|- | |- | ||
|19 | | 19 | ||
|1036.4 | | 1036.4 | ||
|'''Upminor seventh (^m7)'''<br />Diminished octave (d8) | | '''Upminor seventh (^m7)'''<br />Diminished octave (d8) | ||
|'''^C'''<br />Db | | '''^C'''<br />Db | ||
|- | |- | ||
| 20 | | 20 | ||
|1090.9 | | 1090.9 | ||
|Downmajor seventh (vM7)<br />Updiminished octave (^d8)<br />Augmented sixth (A6) | | Downmajor seventh (vM7)<br />Updiminished octave (^d8)<br />Augmented sixth (A6) | ||
|vC#<br />^Db<br />B# | | vC#<br />^Db<br />B# | ||
|- | |- | ||
|21 | | 21 | ||
|1145.5 | | 1145.5 | ||
|Major seventh (M7)<br />Down octave (v8) | | Major seventh (M7)<br />Down octave (v8) | ||
| C#<br />vD | | C#<br />vD | ||
|- | |- | ||
|22 | | 22 | ||
|1200.0 | | 1200.0 | ||
|'''Perfect octave (P8)''' | | '''Perfect octave (P8)''' | ||
|'''D''' | | '''D''' | ||
|} | |} | ||
| Line 494: | Line 487: | ||
[[File:22edo Sagittal.png|800px]] | [[File:22edo Sagittal.png|800px]] | ||
===Superpyth/Porcupine notation=== | === Superpyth/Porcupine notation === | ||
Superpyth/Porcupine notation is a system arising from both superpyth and porcupine temperament. It categorizes each 22edo interval as major and minor of one or both of those temperaments. s indicates superpyth and p indicates porcupine. Because p now represents porcupine and not perfect, P in perfect intervals is no longer used in this system. Instead the number is used without P and is read as either just the number or "Natural". Example: P5 becomes 5 or N5 = Perfect fifth becomes Natural fifth. | Superpyth/Porcupine notation is a system arising from both superpyth and porcupine temperament. It categorizes each 22edo interval as major and minor of one or both of those temperaments. s indicates superpyth and p indicates porcupine. Because p now represents porcupine and not perfect, P in perfect intervals is no longer used in this system. Instead the number is used without P and is read as either just the number or "Natural". Example: P5 becomes 5 or N5 = Perfect fifth becomes Natural fifth. | ||
===Porcupine notation=== | === Porcupine notation === | ||
Porcupine notation uses the porcupine generator to generate the notation as well. The 2nd and 7th are perfect, and the 4th and 5th are imperfect like the 3rd and 6th. The natural notes represent a chain of 2nds ABCDEFG. This is the only way to use a heptatonic notation without additional accidentals. | Porcupine notation uses the porcupine generator to generate the notation as well. The 2nd and 7th are perfect, and the 4th and 5th are imperfect like the 3rd and 6th. The natural notes represent a chain of 2nds ABCDEFG. This is the only way to use a heptatonic notation without additional accidentals. | ||
The keyboard runs {{nowrap|D * * E * * F * * G * * * A * * B * * C * * D}}. | The keyboard runs {{nowrap|D * * E * * F * * G * * * A * * B * * C * * D}}. | ||
===Pentatonic notation=== | === Pentatonic notation === | ||
In Pentatonic notation, the degrees are unison, subthird, fourthoid, fifthoid, subseventh and octoid. The natural notes represent a chain of 5ths FCGDA. This is the only way to use a chain-of-fifths notation without additional accidentals. | In Pentatonic notation, the degrees are unison, subthird, fourthoid, fifthoid, subseventh and octoid. The natural notes represent a chain of 5ths FCGDA. This is the only way to use a chain-of-fifths notation without additional accidentals. | ||
The keyboard runs {{nowrap|D * * * * F * * * G * * * A * * * * C * * * D}}. | The keyboard runs {{nowrap|D * * * * F * * * G * * * A * * * * C * * * D}}. | ||
===Decatonic notation=== | === Decatonic notation === | ||
The Decatonic notation is based on Paul Erlich's decatonic scales. Unlike typical notation, the decatonic system is based on a scale of 10 tones rather than 7. This approach requires an entire re-learning of chords, intervals, and notation, but it allows 22EDO to be notated using only one pair of accidentals, and gives the opportunity to escape a heptatonic thinking pattern. The system is based on two chains of fifths: one represented by Latin letters, the other by Greek. The two chains can be looked at as two juxtaposed pentatonic scales. | The Decatonic notation is based on Paul Erlich's decatonic scales. Unlike typical notation, the decatonic system is based on a scale of 10 tones rather than 7. This approach requires an entire re-learning of chords, intervals, and notation, but it allows 22EDO to be notated using only one pair of accidentals, and gives the opportunity to escape a heptatonic thinking pattern. The system is based on two chains of fifths: one represented by Latin letters, the other by Greek. The two chains can be looked at as two juxtaposed pentatonic scales. | ||
| Line 518: | Line 511: | ||
In this alphabet, a chain of fifths is preserved because equivalent Greek letters also represent fifths if they are the same as their Latin counterparts. For example G–D is a fifth, and so is γ–δ. | In this alphabet, a chain of fifths is preserved because equivalent Greek letters also represent fifths if they are the same as their Latin counterparts. For example G–D is a fifth, and so is γ–δ. | ||
===Comparison of 22edo notation systems=== | === Comparison of 22edo notation systems === | ||
{| class="wikitable center-all right-2" | {| class="wikitable center-all right-2" | ||
|- | |- | ||
![[Degree]] | ! [[Degree]] | ||
![[Cent]]s | ! [[Cent]]s | ||
! colspan="2" |Superpyth/Porcupine | ! colspan="2" | Superpyth/Porcupine | ||
! colspan="3" |Porcupine | ! colspan="3" | Porcupine | ||
! colspan="3" |Pentatonic | ! colspan="3" | Pentatonic | ||
! colspan="3" |Decatonic | ! colspan="3" | Decatonic | ||
! colspan="3" | | ! colspan="3" | [[Ups and downs notation|Ups and Downs]] | ||
[[Ups and downs notation|Ups and Downs]] | ! colspan="3" | [[SKULO interval names]] | ||
! colspan="3" |[[SKULO interval names]] | |||
|- | |- | ||
|0 | | 0 | ||
|0 | | 0 | ||
|Natural Unison | | Natural Unison | ||
|1 | | 1 | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
|natural 1st | | natural 1st | ||
|N1 | | N1 | ||
|C | | C | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
|perfect unison | | perfect unison | ||
|P1 | | P1 | ||
|D | | D | ||
|- | |- | ||
|1 | | 1 | ||
| 55 | | 55 | ||
| s-minor second | | s-minor second | ||
|sm2 | | sm2 | ||
| aug unison | |||
| A1 | |||
| D# | |||
| aug unison | | aug unison | ||
| A1 | |||
| D# | |||
| flat 2nd | |||
|A1 | | f2 | ||
|D# | | C#, δb | ||
|flat 2nd | |||
|f2 | |||
|C#, δb | |||
| up-unison, minor 2nd | | up-unison, minor 2nd | ||
|^1, m2 | | ^1, m2 | ||
|^D, Eb | | ^D, Eb | ||
|comma-wide unison, minor 2nd | | comma-wide unison, minor 2nd | ||
|K1, m2 | | K1, m2 | ||
|KD, Eb | | KD, Eb | ||
|- | |- | ||
|2 | | 2 | ||
|109 | | 109 | ||
|p-diminished second | | p-diminished second | ||
|pd2 | | pd2 | ||
|dim 2nd | | dim 2nd | ||
|d2 | | d2 | ||
|Eb | | Eb | ||
|double-aug unison,<br />double-dim sub3rd | | double-aug unison,<br />double-dim sub3rd | ||
|AA1,<br />dds3 | | AA1,<br />dds3 | ||
|Dx,<br />Fb<span style="vertical-align: super;">3</span> | | Dx,<br />Fb<span style="vertical-align: super;">3</span> | ||
|natural 2nd | | natural 2nd | ||
|N2 | | N2 | ||
|δ | | δ | ||
|downaug 1sn, upminor 2nd | | downaug 1sn, upminor 2nd | ||
|vA1, ^m2 | | vA1, ^m2 | ||
|vD#, ^Eb | | vD#, ^Eb | ||
|classic minor 2nd | | classic minor 2nd | ||
|Km2 | | Km2 | ||
|KEb | | KEb | ||
|- | |- | ||
| 3 | | 3 | ||
|164 | | 164 | ||
|p-minor second | | p-minor second | ||
|pm2 | | pm2 | ||
|perfect 2nd | | perfect 2nd | ||
|P2 | | P2 | ||
|E | | E | ||
| dim sub3rd | | dim sub3rd | ||
|ds3 | | ds3 | ||
|Fbb | | Fbb | ||
| sharp 2nd, flat 3rd | | sharp 2nd, flat 3rd | ||
|s2, f3 | | s2, f3 | ||
|δ#, Db | | δ#, Db | ||
|aug 1sn, downmajor 2nd | | aug 1sn, downmajor 2nd | ||
|A1, vM2 | | A1, vM2 | ||
|D#, vE | | D#, vE | ||
|classic/comma-narrow major 2nd | | classic/comma-narrow major 2nd | ||
|kM2 | | kM2 | ||
|kE | | kE | ||
|- | |- | ||
|4 | | 4 | ||
|218 | | 218 | ||
| (s/p) Major second | | (s/p) Major second | ||
|M2 | | M2 | ||
| aug 2nd | | aug 2nd | ||
|A2 | | A2 | ||
|E# | | E# | ||
|minor sub3rd | | minor sub3rd | ||
|ms3 | | ms3 | ||
|Fb | | Fb | ||
|natural 3rd | | natural 3rd | ||
|N3 | | N3 | ||
|D | | D | ||
|major 2nd | | major 2nd | ||
|M2 | | M2 | ||
|E | | E | ||
|major 2nd | | major 2nd | ||
|M2 | | M2 | ||
|E | | E | ||
|- | |- | ||
|5 | | 5 | ||
|273 | | 273 | ||
|s-minor third | | s-minor third | ||
| sm3 | | sm3 | ||
| dim 3rd | | dim 3rd | ||
| d3 | | d3 | ||
|Fb | | Fb | ||
|major sub3rd | | major sub3rd | ||
|Ms3 | | Ms3 | ||
|F | | F | ||
|sharp 3rd | | sharp 3rd | ||
|s3 | | s3 | ||
|D# | | D# | ||
|minor 3rd | | minor 3rd | ||
|m3 | | m3 | ||
|F | | F | ||
|minor 3rd | | minor 3rd | ||
|m3 | | m3 | ||
|F | | F | ||
|- | |- | ||
|6 | | 6 | ||
|327 | | 327 | ||
|p-minor third | | p-minor third | ||
|pm3 | | pm3 | ||
|minor 3rd | | minor 3rd | ||
|m3 | | m3 | ||
|F | | F | ||
|aug sub3rd | | aug sub3rd | ||
| As3 | | As3 | ||
| F# | | F# | ||
|flat 4th | | flat 4th | ||
|f4 | | f4 | ||
|εb | | εb | ||
|upminor 3rd | | upminor 3rd | ||
|^m3 | | ^m3 | ||
|^F | | ^F | ||
|classic minor 3rd | | classic minor 3rd | ||
|Km3 | | Km3 | ||
|KF | | KF | ||
|- | |- | ||
|7 | | 7 | ||
|382 | | 382 | ||
|p-Major third | | p-Major third | ||
|pM3 | | pM3 | ||
|major 3rd | | major 3rd | ||
|M3 | | M3 | ||
|F# | | F# | ||
|double-aug sub3rd,<br />double-dim 4thoid | | double-aug sub3rd,<br />double-dim 4thoid | ||
| AAs3,<br />dd4d | | AAs3,<br />dd4d | ||
|Fx,<br />Gbb | | Fx,<br />Gbb | ||
|natural 4th | | natural 4th | ||
|N4 | | N4 | ||
| ε | | ε | ||
|downmajor 3rd | | downmajor 3rd | ||
|vM3 | | vM3 | ||
| vF# | | vF# | ||
|classic major 3rd | | classic major 3rd | ||
| kM3 | | kM3 | ||
| kF# | | kF# | ||
| Line 694: | Line 686: | ||
| 436 | | 436 | ||
| s-Major third | | s-Major third | ||
|sM3 | | sM3 | ||
| aug 3rd, dim 4th | | aug 3rd, dim 4th | ||
|A3, d4 | | A3, d4 | ||
|Fx, Gb | | Fx, Gb | ||
|dim 4thoid | | dim 4thoid | ||
|d4d | | d4d | ||
| Gb | | Gb | ||
| sharp 4th, flat 5th | | sharp 4th, flat 5th | ||
| s4, f5 | | s4, f5 | ||
|ε#, Eb | | ε#, Eb | ||
|major 3rd | | major 3rd | ||
|M3 | | M3 | ||
|F# | | F# | ||
|major 3rd | | major 3rd | ||
|M3 | | M3 | ||
|F# | | F# | ||
|- | |- | ||
| 9 | | 9 | ||
|491 | | 491 | ||
|Natural Fourth | | Natural Fourth | ||
|4, N4 | | 4, N4 | ||
|minor 4th | | minor 4th | ||
|m4 | | m4 | ||
|G | | G | ||
| perfect 4thoid | | perfect 4thoid | ||
| P4d | | P4d | ||
| G | | G | ||
|natural 5th | | natural 5th | ||
|N5 | | N5 | ||
| E | | E | ||
|perfect 4th | | perfect 4th | ||
|P4 | | P4 | ||
| G | |||
| perfect 4th | |||
| P4 | |||
| G | | G | ||
|- | |- | ||
| 10 | | 10 | ||
| 545 | | 545 | ||
| p-Major fourth, s-dim fifth | | p-Major fourth, s-dim fifth | ||
|pM4, sd5 | | pM4, sd5 | ||
| major 4th | | major 4th | ||
|M4 | | M4 | ||
|G# | | G# | ||
|aug 4thoid | | aug 4thoid | ||
|A4d | | A4d | ||
|G# | | G# | ||
| sharp 5th, flat 6th | | sharp 5th, flat 6th | ||
| s5, f6 | | s5, f6 | ||
| E#, γb | | E#, γb | ||
|up-4th, dim 5th | | up-4th, dim 5th | ||
|^4, d5 | | ^4, d5 | ||
|^G, Ab | | ^G, Ab | ||
| comma-wide 4th | | comma-wide 4th | ||
|K4 | | K4 | ||
|KG | | KG | ||
|- | |- | ||
|11 | | 11 | ||
|600 | | 600 | ||
|p-Augmented Fourth,<br />p-diminished Fifth,<br />Half-Octave | | p-Augmented Fourth,<br />p-diminished Fifth,<br />Half-Octave | ||
|A4, HO | | A4, HO | ||
|aug 4th, <br />dim 5th | | aug 4th, <br />dim 5th | ||
|A4, d5 | | A4, d5 | ||
|Gx, <br />Abb | | Gx, <br />Abb | ||
|double-aug 4thoid,<br />double-dim 5thoid | | double-aug 4thoid,<br />double-dim 5thoid | ||
|AA4d, <br />dd5d | | AA4d, <br />dd5d | ||
|Gx, <br />Abb | | Gx, <br />Abb | ||
|natural 6th | | natural 6th | ||
|N6 | | N6 | ||
| γ | | γ | ||
| downaug 4th, updim 5th | | downaug 4th, updim 5th | ||
|vA4, ^d5 | | vA4, ^d5 | ||
| vG#, ^Ab | | vG#, ^Ab | ||
|comma-narrow augmented 4th<br />comma-wide diminished 5th | | comma-narrow augmented 4th<br />comma-wide diminished 5th | ||
|kA4<br />Kd5 | | kA4<br />Kd5 | ||
|kG#, KAb | | kG#, KAb | ||
|- | |- | ||
| 12 | | 12 | ||
| 655 | | 655 | ||
| p-minor Fifth, s-aug Fourth | | p-minor Fifth, s-aug Fourth | ||
|pm5, sA4 | | pm5, sA4 | ||
| minor 5th | | minor 5th | ||
|m5 | | m5 | ||
|Ab | | Ab | ||
|dim 5thoid | | dim 5thoid | ||
|d5d | | d5d | ||
| Ab | | Ab | ||
| sharp 6th, flat 7th | | sharp 6th, flat 7th | ||
|s6, f7 | | s6, f7 | ||
|γ#, Gb | | γ#, Gb | ||
|aug 4th, down-5th | | aug 4th, down-5th | ||
|A4, v5 | | A4, v5 | ||
| G#, vA | | G#, vA | ||
|comma-narrow 5th | | comma-narrow 5th | ||
|k5 | | k5 | ||
|kA | | kA | ||
|- | |- | ||
| 13 | | 13 | ||
|709 | | 709 | ||
| Natural Fifth | | Natural Fifth | ||
|5, N5 | | 5, N5 | ||
|major 5th | | major 5th | ||
|M5 | | M5 | ||
|A | | A | ||
| perfect 5thoid | | perfect 5thoid | ||
| P5d | | P5d | ||
| A | | A | ||
|natural 7th | | natural 7th | ||
|N7 | | N7 | ||
| G | | G | ||
|perfect 5th | | perfect 5th | ||
|P5 | | P5 | ||
| A | |||
| perfect 5th | |||
| P5 | |||
| A | | A | ||
|- | |- | ||
|14 | | 14 | ||
| 764 | | 764 | ||
| s-minor sixth | | s-minor sixth | ||
|sm6 | | sm6 | ||
|aug 5th, dim 6th | | aug 5th, dim 6th | ||
|A5, d6 | | A5, d6 | ||
|A#, Bbb | | A#, Bbb | ||
| aug 5thoid | | aug 5thoid | ||
|A5d | | A5d | ||
|A# | | A# | ||
|sharp 7th | | sharp 7th | ||
|s7 | | s7 | ||
|G# | | G# | ||
|minor 6th | | minor 6th | ||
|m6 | | m6 | ||
| Bb | | Bb | ||
|minor 6th | | minor 6th | ||
|m6 | | m6 | ||
| Bb | | Bb | ||
|- | |- | ||
|15 | | 15 | ||
|818 | | 818 | ||
|p-minor sixth | | p-minor sixth | ||
|pm6 | | pm6 | ||
|minor 6th | | minor 6th | ||
|m6 | | m6 | ||
|Bb | | Bb | ||
|double-aug 5thoid,<br />double-dim sub7th | | double-aug 5thoid,<br />double-dim sub7th | ||
|AA5d,<br />dds7 | | AA5d,<br />dds7 | ||
|Ax,<br />Cb<span style="vertical-align: super;">3</span> | | Ax,<br />Cb<span style="vertical-align: super;">3</span> | ||
|flat 8th | | flat 8th | ||
|f8 | | f8 | ||
|αb | | αb | ||
|upminor 6th | | upminor 6th | ||
|^m6 | | ^m6 | ||
| ^Bb | | ^Bb | ||
|classic minor 6th | | classic minor 6th | ||
|Km6 | | Km6 | ||
|KBb | | KBb | ||
|- | |- | ||
|16 | | 16 | ||
|873 | | 873 | ||
|p-Major sixth | | p-Major sixth | ||
|pM6 | | pM6 | ||
|major 6th | | major 6th | ||
|M6 | | M6 | ||
|B | | B | ||
|dim sub7th | | dim sub7th | ||
|ds7 | | ds7 | ||
|Cbb | | Cbb | ||
|natural 8th | | natural 8th | ||
|N8 | | N8 | ||
|α | | α | ||
| downmajor 6th | | downmajor 6th | ||
|vM6 | | vM6 | ||
|vB | | vB | ||
|classic major 6th | | classic major 6th | ||
| kM6 | | kM6 | ||
| kB | | kB | ||
|- | |- | ||
|17 | | 17 | ||
|927 | | 927 | ||
|s-Major sixth | | s-Major sixth | ||
| sM6 | | sM6 | ||
| aug 6th | | aug 6th | ||
|A6 | | A6 | ||
|B# | | B# | ||
|minor sub7th | | minor sub7th | ||
|ms7 | | ms7 | ||
| Cb | | Cb | ||
| sharp 8th, flat 9th | | sharp 8th, flat 9th | ||
|s8, f9 | | s8, f9 | ||
|α#, Ab | | α#, Ab | ||
| major 6th | | major 6th | ||
|M6 | | M6 | ||
|B | | B | ||
| major 6th | |||
| M6 | |||
| B | |||
|- | |- | ||
|18 | | 18 | ||
|982 | | 982 | ||
|(s/p) minor seventh | | (s/p) minor seventh | ||
|m7 | | m7 | ||
| dim 7th | | dim 7th | ||
|d7 | | d7 | ||
|Cb | | Cb | ||
|major sub7th | | major sub7th | ||
|Ms7 | | Ms7 | ||
|C | | C | ||
|natural 9th | | natural 9th | ||
|N9 | | N9 | ||
|A | | A | ||
|minor 7th | | minor 7th | ||
|m7 | | m7 | ||
|C | | C | ||
|minor 7th | | minor 7th | ||
|m7 | | m7 | ||
|C | | C | ||
|- | |- | ||
|19 | | 19 | ||
|1036 | | 1036 | ||
|p-Major seventh | | p-Major seventh | ||
|pM7 | | pM7 | ||
|perfect 7th | | perfect 7th | ||
|P7 | | P7 | ||
|C | | C | ||
|aug sub7th | | aug sub7th | ||
|As7 | | As7 | ||
|C# | | C# | ||
|sharp 9th, flat 10th | | sharp 9th, flat 10th | ||
|s9, f10 | | s9, f10 | ||
|A#, βb | | A#, βb | ||
|upminor 7th, dim 8ve | | upminor 7th, dim 8ve | ||
|^m7, d8 | | ^m7, d8 | ||
|^C, Db | | ^C, Db | ||
|classic minor 7th | | classic minor 7th | ||
|Km7 | | Km7 | ||
|kC | | kC | ||
|- | |- | ||
|20 | | 20 | ||
|1091 | | 1091 | ||
|p-Augmented seventh | | p-Augmented seventh | ||
|pA7 | | pA7 | ||
|aug 7th | | aug 7th | ||
|A7 | | A7 | ||
|C# | | C# | ||
|double-aug sub7th,<br />double-dim octave | | double-aug sub7th,<br />double-dim octave | ||
|AAs7,<br />dd8 | | AAs7,<br />dd8 | ||
| Cx,<br />Dbb | | Cx,<br />Dbb | ||
| natural 10th | | natural 10th | ||
|N10 | | N10 | ||
|β | | β | ||
|downmajor 7th, updim 8ve | | downmajor 7th, updim 8ve | ||
|vM7, ^d8 | | vM7, ^d8 | ||
|vC#, ^Db | | vC#, ^Db | ||
|classic major 7th | | classic major 7th | ||
|kM7 | | kM7 | ||
|kC# | | kC# | ||
|- | |- | ||
|21 | | 21 | ||
| 1145 | | 1145 | ||
|s-Major seventh | | s-Major seventh | ||
|sM7 | | sM7 | ||
|dim 8ve | | dim 8ve | ||
|d8 | | d8 | ||
| Db | |||
| dim octave | |||
| d8 | |||
| Db | | Db | ||
| sharp 10th | |||
| s10 | |||
|sharp 10th | |||
|s10 | |||
| β#, Cb | | β#, Cb | ||
|major 7th, down 8ve | | major 7th, down 8ve | ||
|M7, v8 | | M7, v8 | ||
|C#, vD | | C#, vD | ||
| major 7th / comma-narrow 8ve | | major 7th / comma-narrow 8ve | ||
|M7 / k8 | | M7 / k8 | ||
|C#, kD | | C#, kD | ||
|- | |- | ||
|22 | | 22 | ||
|1200 | | 1200 | ||
|Octave | | Octave | ||
|8 | | 8 | ||
| perfect octave | | perfect octave | ||
|P8 | | P8 | ||
|D | | D | ||
|natural 11th | | perfect octave | ||
|N11 | | P8 | ||
|C | | D | ||
|perfect octave | | natural 11th | ||
|P8 | | N11 | ||
|D | | C | ||
|perfect 8ve | | perfect octave | ||
|P8 | | P8 | ||
|D | | D | ||
| perfect 8ve | |||
| P8 | |||
| D | |||
|} | |} | ||
==Approximation to JI== | == Approximation to JI == | ||
[[File:22ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 17-limit intervals approximated in 22edo]] | [[File:22ed2.svg|250px|thumb|right|alt=alt : Your browser has no SVG support.|Selected 17-limit intervals approximated in 22edo]] | ||
===Interval mappings=== | === Interval mappings === | ||
{{Q-odd-limit intervals|22}} | {{Q-odd-limit intervals|22}} | ||
===Zeta peak index === | === Zeta peak index === | ||
{| class="wikitable center-all" | {| class="wikitable center-all" | ||
|- | |- | ||
! colspan="3" |Tuning | ! colspan="3" | Tuning | ||
! colspan="3" |Strength | ! colspan="3" | Strength | ||
! colspan="2" |Closest edo | ! colspan="2" | Closest edo | ||
! colspan="2" |Integer limit | ! colspan="2" | Integer limit | ||
|- | |- | ||
!ZPI | ! ZPI | ||
!Steps per octave | ! Steps per octave | ||
!Step size (cents) | ! Step size (cents) | ||
!Height | ! Height | ||
!Integral | ! Integral | ||
!Gap | ! Gap | ||
!Edo | ! Edo | ||
!Octave (cents) | ! Octave (cents) | ||
!Consistent | ! Consistent | ||
!Distinct | ! Distinct | ||
|- | |- | ||
|[[80zpi]] | | [[80zpi]] | ||
|22.0251467420146 | | 22.0251467420146 | ||
| 54.4831784348982 | | 54.4831784348982 | ||
|6.062600 | | 6.062600 | ||
|1.258178 | | 1.258178 | ||
|16.213941 | | 16.213941 | ||
| 22edo | | 22edo | ||
|1198.62992556776 | | 1198.62992556776 | ||
|12 | | 12 | ||
|8 | | 8 | ||
|} | |} | ||
==Defining features== | == Defining features == | ||
=== Septimal vs. syntonic comma=== | === Septimal vs. syntonic comma === | ||
Possibly the most striking characteristic of 22edo to those not used to it is that it does '''not''' temper out the syntonic comma of 81/80. This means that 22 is not a system of [[meantone]] temperament, and as such it distinguishes a number of [[3-limit]] and [[5-limit]] intervals that meantone tunings (most notably 12edo, 19edo, 31edo, and 43edo) do not distinguish, such as the two whole tones of 9/8 and 10/9. Indeed, these distinctions are significantly exaggerated in 22edo and [[27edo]] in comparison to 5-limit JI and many more accurate temperaments such as [[34edo]], [[41edo]], and [[53edo]], allowing many opportunities for alternate interpretations of their harmony. | Possibly the most striking characteristic of 22edo to those not used to it is that it does '''not''' temper out the syntonic comma of 81/80. This means that 22 is not a system of [[meantone]] temperament, and as such it distinguishes a number of [[3-limit]] and [[5-limit]] intervals that meantone tunings (most notably 12edo, 19edo, 31edo, and 43edo) do not distinguish, such as the two whole tones of 9/8 and 10/9. Indeed, these distinctions are significantly exaggerated in 22edo and [[27edo]] in comparison to 5-limit JI and many more accurate temperaments such as [[34edo]], [[41edo]], and [[53edo]], allowing many opportunities for alternate interpretations of their harmony. | ||
The diatonic scale it produces is instead derived from [[superpyth]] temperament. Despite having the same melodic structure as meantone's diatonic scale (LLsLLLs or, [[5L 2s]]), superpyth's diatonic scale has subminor and supermajor thirds of 7/6 and 9/7, rather than minor and major thirds of 6/5 and 5/4. This means that the septimal comma of 64/63 is tempered out, rather than the syntonic comma of 81/80, one of 22et's core features. Superpyth is melodically interesting in that intervals such as A–G♮ and C–B♭ are ''harmonic'' sevenths instead of 5-limit minor sevenths (approximately [[7/4]] instead of [[9/5]]), in addition to having a quasi-equal pentatonic scale (as the major whole tone and subminor third are rather close in size) and more uneven diatonic scale, as compared with 12et and other meantone systems; the step patterns in 22et are {{dash|4, 4, 5, 4, 5|med}} and {{dash|4, 4, 1, 4, 4, 4, 1|med}}, respectively. | The diatonic scale it produces is instead derived from [[superpyth]] temperament. Despite having the same melodic structure as meantone's diatonic scale (LLsLLLs or, [[5L 2s]]), superpyth's diatonic scale has subminor and supermajor thirds of 7/6 and 9/7, rather than minor and major thirds of 6/5 and 5/4. This means that the septimal comma of 64/63 is tempered out, rather than the syntonic comma of 81/80, one of 22et's core features. Superpyth is melodically interesting in that intervals such as A–G♮ and C–B♭ are ''harmonic'' sevenths instead of 5-limit minor sevenths (approximately [[7/4]] instead of [[9/5]]), in addition to having a quasi-equal pentatonic scale (as the major whole tone and subminor third are rather close in size) and more uneven diatonic scale, as compared with 12et and other meantone systems; the step patterns in 22et are {{dash|4, 4, 5, 4, 5|med}} and {{dash|4, 4, 1, 4, 4, 4, 1|med}}, respectively. | ||
===Porcupine comma=== | === Porcupine comma === | ||
It additionally tempers out the porcupine comma or maximal diesis of 250/243, which means that 22edo [[support]]s [[porcupine]] temperament. The generator for porcupine is a very flat minor whole tone of ~[[10/9]] (usually tuned slightly flat of [[11/10]]), two of which is a sharp ~[[6/5]], and three of which is a slightly flat ~[[4/3]], implying the existence of an equal-step tetrachord, which is characteristic of porcupine. It can be observed that the tuning damage that porcupine tempering implies (the ones just described) is highly characteristic of the tuning properties of 22edo and as such represents one excellent point of departure for examining the harmonic properties of 22edo. It forms [[mos scale]]s of 7 and 8, which in 22edo are tuned respectively as {{dash|4, 3, 3, 3, 3, 3, 3|med}} and {{dash|1, 3, 3, 3, 3, 3, 3, 3|med}} (and their respective modes). | It additionally tempers out the porcupine comma or maximal diesis of 250/243, which means that 22edo [[support]]s [[porcupine]] temperament. The generator for porcupine is a very flat minor whole tone of ~[[10/9]] (usually tuned slightly flat of [[11/10]]), two of which is a sharp ~[[6/5]], and three of which is a slightly flat ~[[4/3]], implying the existence of an equal-step tetrachord, which is characteristic of porcupine. It can be observed that the tuning damage that porcupine tempering implies (the ones just described) is highly characteristic of the tuning properties of 22edo and as such represents one excellent point of departure for examining the harmonic properties of 22edo. It forms [[mos scale]]s of 7 and 8, which in 22edo are tuned respectively as {{dash|4, 3, 3, 3, 3, 3, 3|med}} and {{dash|1, 3, 3, 3, 3, 3, 3, 3|med}} (and their respective modes). | ||
===5-limit commas=== | === 5-limit commas === | ||
Other 5-limit commas 22edo tempers out include the diaschisma, [[2048/2025]] and the magic comma or small diesis, [[3125/3072]]. In a diaschismic system, such as 12et or 22et, the diatonic tritone [[45/32]], which is a major third above a major whole tone representing [[9/8]], is equated to its inverted form, [[64/45]]. That the magic comma is tempered out means that 22et is a magic system, where five major thirds make up a perfect fifth. | Other 5-limit commas 22edo tempers out include the diaschisma, [[2048/2025]] and the magic comma or small diesis, [[3125/3072]]. In a diaschismic system, such as 12et or 22et, the diatonic tritone [[45/32]], which is a major third above a major whole tone representing [[9/8]], is equated to its inverted form, [[64/45]]. That the magic comma is tempered out means that 22et is a magic system, where five major thirds make up a perfect fifth. | ||
===7-limit commas=== | === 7-limit commas === | ||
In the 7-limit 22edo tempers out certain commas also tempered out by 12et; this relates 12et to 22 in a way different from the way in which meantone systems are akin to it. [[50/49]] (the jubilisma), and 64/63 (the septimal comma) are tempered out in both systems, so they both equate the two septimal tritones of 7/5 and 10/7, and because of 64/63 the dominant seventh chord and an otonal tetrad are represented by the same chord. Hence both also temper out {{nowrap|(50/49)/(64/63) {{=}} 225/224}}, the [[septimal kleisma]], so that the septimal kleisma augmented triad is a chord of 22et, as it also is of any meantone tuning. A septimal comma not tempered out by 12et which 22et does temper out is 1728/1715, the [[1728/1715|orwell comma]]; and the [[orwell tetrad]] is also a chord of 22et. | In the 7-limit 22edo tempers out certain commas also tempered out by 12et; this relates 12et to 22 in a way different from the way in which meantone systems are akin to it. [[50/49]] (the jubilisma), and 64/63 (the septimal comma) are tempered out in both systems, so they both equate the two septimal tritones of 7/5 and 10/7, and because of 64/63 the dominant seventh chord and an otonal tetrad are represented by the same chord. Hence both also temper out {{nowrap|(50/49)/(64/63) {{=}} 225/224}}, the [[septimal kleisma]], so that the septimal kleisma augmented triad is a chord of 22et, as it also is of any meantone tuning. A septimal comma not tempered out by 12et which 22et does temper out is 1728/1715, the [[1728/1715|orwell comma]]; and the [[orwell tetrad]] is also a chord of 22et. | ||
===11-limit commas=== | === 11-limit commas=== | ||
In the 11-limit, 22edo tempers out the [[quartisma]], leading to a stack of five 33/32 quartertones being equated with one 7/6 subminor third. This is a trait which, while shared with [[24edo]], is surprisingly ''not'' shared with a number of other relatively small edos such as [[17edo]], [[26edo]] and [[34edo]]. In fact, not even the famous [[53edo]] has this property—although it should be noted that the related [[159edo]] ''does''. | In the 11-limit, 22edo tempers out the [[quartisma]], leading to a stack of five 33/32 quartertones being equated with one 7/6 subminor third. This is a trait which, while shared with [[24edo]], is surprisingly ''not'' shared with a number of other relatively small edos such as [[17edo]], [[26edo]] and [[34edo]]. In fact, not even the famous [[53edo]] has this property—although it should be noted that the related [[159edo]] ''does''. | ||
===Other features=== | === Other features === | ||
The 163.6¢ "flat minor whole tone" is a key interval in 22edo, in part because it functions as no less than three different consonant ratios in the [[11-limit]]: 10/9, 11/10, and 12/11. It is thus extremely ambiguous and flexible. The trade-off is that it is very much in the cracks of the 12-equal piano, and so for most 12-equal listeners, it takes some getting used to. Simple translations of 5-limit music into 22edo can sound very different, with a more complex harmonic quality inevitably arising. 22edo does not contain a neutral third but both the 5-limit thirds have a "neutral-like" quality since they are tempered closer together rather than farther apart as in 12edo. | The 163.6¢ "flat minor whole tone" is a key interval in 22edo, in part because it functions as no less than three different consonant ratios in the [[11-limit]]: 10/9, 11/10, and 12/11. It is thus extremely ambiguous and flexible. The trade-off is that it is very much in the cracks of the 12-equal piano, and so for most 12-equal listeners, it takes some getting used to. Simple translations of 5-limit music into 22edo can sound very different, with a more complex harmonic quality inevitably arising. 22edo does not contain a neutral third but both the 5-limit thirds have a "neutral-like" quality since they are tempered closer together rather than farther apart as in 12edo. | ||
| Line 1,054: | Line 1,046: | ||
22edo is melodically similar to [[24edo]] as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In [[Sagittal notation]], 11 can be notated as every other note of 22. | 22edo is melodically similar to [[24edo]] as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In [[Sagittal notation]], 11 can be notated as every other note of 22. | ||
==Regular temperament properties == | == Regular temperament properties == | ||
{| class="wikitable center-4 center-5 center-6" | {| class="wikitable center-4 center-5 center-6" | ||
|- | |- | ||
! rowspan="2" |[[Subgroup]] | ! rowspan="2" | [[Subgroup]] | ||
! rowspan="2" |[[Comma list]] | ! rowspan="2" | [[Comma list]] | ||
! rowspan="2" |[[Mapping]] | ! rowspan="2" | [[Mapping]] | ||
! rowspan="2" |Optimal<br>8ve stretch (¢) | ! rowspan="2" | Optimal<br>8ve stretch (¢) | ||
! colspan="2" |Tuning error | ! colspan="2" | Tuning error | ||
|- | |- | ||
! [[TE error|Absolute]] (¢) | ! [[TE error|Absolute]] (¢) | ||
![[TE simple badness|Relative]] (%) | ! [[TE simple badness|Relative]] (%) | ||
|- | |- | ||
| 2.3 | | 2.3 | ||
| | | {{monzo| 35 -22 }} | ||
{{monzo| 35 -22 }} | | {{mapping| 22 35 }} | ||
|{{mapping| 22 35 }} | | −2.25 | ||
|−2.25 | | 2.25 | ||
|2.25 | | 4.12 | ||
|4.12 | |||
|- | |- | ||
|2.3.5 | | 2.3.5 | ||
| 250/243, 2048/2025 | | 250/243, 2048/2025 | ||
|{{mapping| 22 35 51 }} | | {{mapping| 22 35 51 }} | ||
|−0.86 | | −0.86 | ||
| 2.70 | | 2.70 | ||
|4.94 | | 4.94 | ||
|- | |- | ||
|2.3.5.7 | | 2.3.5.7 | ||
| 50/49, 64/63, 245/243 | | 50/49, 64/63, 245/243 | ||
|{{mapping| 22 35 51 62 }} | | {{mapping| 22 35 51 62 }} | ||
|−1.80 | | −1.80 | ||
|2.85 | | 2.85 | ||
|5.23 | | 5.23 | ||
|- | |- | ||
|2.3.5.7.11 | | 2.3.5.7.11 | ||
|50/49, 55/54, 64/63, 99/98 | | 50/49, 55/54, 64/63, 99/98 | ||
| {{mapping| 22 35 51 62 76 }} | | {{mapping| 22 35 51 62 76 }} | ||
|−1.11 | | −1.11 | ||
|2.90 | | 2.90 | ||
|5.33 | | 5.33 | ||
|- | |- | ||
|2.3.5.7.11.17 | | 2.3.5.7.11.17 | ||
|50/49, 55/54, 64/63, 85/84, 99/98 | | 50/49, 55/54, 64/63, 85/84, 99/98 | ||
|{{mapping| 22 35 51 62 76 90 }} | | {{mapping| 22 35 51 62 76 90 }} | ||
| −1.09 | | −1.09 | ||
|2.65 | | 2.65 | ||
|4.87 | | 4.87 | ||
|} | |} | ||
* 22et is lower in relative error than any previous equal temperaments in the 11-limit. The next equal temperament that does better in this subgroup is [[31edo|31]]. | * 22et is lower in relative error than any previous equal temperaments in the 11-limit. The next equal temperament that does better in this subgroup is [[31edo|31]]. | ||
*22et does best in the 2.3.5.7.11.17 subgroup, and the next equal temperament that does better in this subgroup is [[46edo|46]]. | * 22et does best in the 2.3.5.7.11.17 subgroup, and the next equal temperament that does better in this subgroup is [[46edo|46]]. | ||
===Uniform maps=== | === Uniform maps === | ||
{{Uniform map|13|21.5|22.5}} | {{Uniform map|13|21.5|22.5}} | ||
===Commas=== | === Commas === | ||
22et [[tempering out|tempers out]] the following [[commas]]. This assumes the [[val]] {{val| 22 35 51 62 76 81 }}. | 22et [[tempering out|tempers out]] the following [[commas]]. This assumes the [[val]] {{val| 22 35 51 62 76 81 }}. | ||
{| class="commatable wikitable center-all left-3 right-4 left-6" | {| class="commatable wikitable center-all left-3 right-4 left-6" | ||
|- | |- | ||
![[Harmonic limit|Prime<br>limit]] | ! [[Harmonic limit|Prime<br>limit]] | ||
![[Ratio]]<ref group="note">{{rd}}</ref> | ! [[Ratio]]<ref group="note">{{rd}}</ref> | ||
! [[Monzo]] | ! [[Monzo]] | ||
! | ! [[Cents]] | ||
[[Cents]] | ! [[Color name]] | ||
![[Color name]] | ! Name | ||
!Name | |||
|- | |- | ||
|3 | | 3 | ||
|<abbr title="34359738368/31381059609">(22 digits)</abbr> | | <abbr title="34359738368/31381059609">(22 digits)</abbr> | ||
|{{monzo| 35 -22 }} | | {{monzo| 35 -22 }} | ||
|156.98 | | 156.98 | ||
|Trisawa | | Trisawa | ||
|22-comma | | 22-comma | ||
|- | |- | ||
|5 | | 5 | ||
|[[20480/19683]] | | [[20480/19683]] | ||
|{{monzo| 12 -9 1 }} | | {{monzo| 12 -9 1 }} | ||
|68.72 | | 68.72 | ||
|Sayo | | Sayo | ||
|Superpyth comma | | Superpyth comma | ||
|- | |- | ||
|5 | | 5 | ||
| | | [[250/243]] | ||
[[250/243]] | | {{monzo| 1 -5 3 }} | ||
|{{monzo| 1 -5 3 }} | |||
| 49.17 | | 49.17 | ||
|Triyo | | Triyo | ||
| Porcupine comma | | Porcupine comma | ||
|- | |- | ||
|5 | | 5 | ||
|[[3125/3072]] | | [[3125/3072]] | ||
| {{monzo|-10 -1 5 }} | | {{monzo|-10 -1 5 }} | ||
|29.61 | | 29.61 | ||
|Laquinyo | | Laquinyo | ||
|Magic comma | | Magic comma | ||
|- | |- | ||
|5 | | 5 | ||
|[[2048/2025]] | | [[2048/2025]] | ||
|{{monzo| 11 -4 -2 }} | | {{monzo| 11 -4 -2 }} | ||
|19.55 | | 19.55 | ||
|Sagugu | | Sagugu | ||
|Diaschisma | | Diaschisma | ||
|- | |- | ||
|5 | | 5 | ||
|[[2109375/2097152| (14 digits)]] | | [[2109375/2097152| (14 digits)]] | ||
|{{monzo|-21 3 7 }} | | {{monzo|-21 3 7 }} | ||
| 10.06 | | 10.06 | ||
|Lasepyo | | Lasepyo | ||
|[[Semicomma]] | | [[Semicomma]] | ||
|- | |- | ||
|5 | | 5 | ||
|<abbr title="4294967296/4271484375">(20 digits)</abbr> | | <abbr title="4294967296/4271484375">(20 digits)</abbr> | ||
|{{monzo| 32 -7 -9 }} | | {{monzo| 32 -7 -9 }} | ||
|9.49 | | 9.49 | ||
|Sasa-tritrigu | | Sasa-tritrigu | ||
|[[Escapade comma]] | | [[Escapade comma]] | ||
|- | |- | ||
|5 | | 5 | ||
|<abbr title="9010162353515625/9007199254740992">(32 digits)</abbr> | | <abbr title="9010162353515625/9007199254740992">(32 digits)</abbr> | ||
|{{monzo|-53 10 16 }} | | {{monzo|-53 10 16 }} | ||
|0.57 | | 0.57 | ||
| Quadla-quadquadyo | | Quadla-quadquadyo | ||
|[[Kwazy comma]] | | [[Kwazy comma]] | ||
|- | |- | ||
|7 | | 7 | ||
| | | [[50/49]] | ||
[[50/49]] | | {{monzo| 1 0 2 -2 }} | ||
|{{monzo| 1 0 2 -2 }} | | 34.98 | ||
|34.98 | | Biruyo | ||
|Biruyo | | Jubilisma | ||
|Jubilisma | |||
|- | |- | ||
|7 | | 7 | ||
|[[64/63]] | | [[64/63]] | ||
|{{monzo| 6 -2 0 -1 }} | | {{monzo| 6 -2 0 -1 }} | ||
|27.26 | | 27.26 | ||
|Ru | | Ru | ||
|Septimal comma | | Septimal comma | ||
|- | |- | ||
| 7 | | 7 | ||
|[[875/864]] | | [[875/864]] | ||
| {{monzo|-5 -3 3 1 }} | | {{monzo|-5 -3 3 1 }} | ||
|21.90 | | 21.90 | ||
| Zotriyo | | Zotriyo | ||
|Keema | | Keema | ||
|- | |- | ||
|7 | | 7 | ||
|[[2430/2401]] | | [[2430/2401]] | ||
|{{monzo| 1 5 1 -4 }} | | {{monzo| 1 5 1 -4 }} | ||
|20.79 | | 20.79 | ||
|Quadru-ayo | | Quadru-ayo | ||
|Nuwell comma | | Nuwell comma | ||
|- | |- | ||
| 7 | | 7 | ||
|[[245/243]] | | [[245/243]] | ||
|{{monzo| 0 -5 1 2 }} | | {{monzo| 0 -5 1 2 }} | ||
|14.19 | | 14.19 | ||
|Zozoyo | | Zozoyo | ||
|Sensamagic comma | | Sensamagic comma | ||
|- | |- | ||
|7 | | 7 | ||
|[[1728/1715]] | | [[1728/1715]] | ||
|{{monzo| 6 3 -1 -3 }} | | {{monzo| 6 3 -1 -3 }} | ||
|13.07 | | 13.07 | ||
|Triru-agu | | Triru-agu | ||
|Orwellisma | | Orwellisma | ||
|- | |- | ||
| 7 | | 7 | ||
|[[225/224]] | | [[225/224]] | ||
|{{monzo|-5 2 2 -1 }} | | {{monzo|-5 2 2 -1 }} | ||
|7.71 | | 7.71 | ||
|Ruyoyo | | Ruyoyo | ||
|Marvel comma | | Marvel comma | ||
|- | |- | ||
| 7 | | 7 | ||
|[[10976/10935]] | | [[10976/10935]] | ||
| | | {{monzo| 5 -7 -1 3 }} | ||
{{monzo| 5 -7 -1 3 }} | | 6.48 | ||
|6.48 | | Trizo-agu | ||
|Trizo-agu | | Hemimage comma | ||
|Hemimage comma | |||
|- | |- | ||
|7 | | 7 | ||
| [[6144/6125]] | | [[6144/6125]] | ||
|{{monzo| 11 1 -3 -2 }} | | {{monzo| 11 1 -3 -2 }} | ||
|5.36 | | 5.36 | ||
|Saruru-atrigu | | Saruru-atrigu | ||
| Porwell comma | | Porwell comma | ||
|- | |- | ||
|7 | | 7 | ||
| [[65625/65536]] | | [[65625/65536]] | ||
| | | {{monzo|-16 1 5 1 }} | ||
{{monzo|-16 1 5 1 }} | | 2.35 | ||
|2.35 | | Lazoquinyo | ||
|Lazoquinyo | | Horwell comma | ||
|Horwell comma | |||
|- | |- | ||
|7 | | 7 | ||
|<abbr title="420175/419904">(12 digits)</abbr> | | <abbr title="420175/419904">(12 digits)</abbr> | ||
|{{monzo|-6 -8 2 5 }} | | {{monzo|-6 -8 2 5 }} | ||
|1.12 | | 1.12 | ||
|Quinzo-ayoyo | | Quinzo-ayoyo | ||
|[[Wizma]] | | [[Wizma]] | ||
|- | |- | ||
|11 | | 11 | ||
|[[99/98]] | | [[99/98]] | ||
|{{monzo|-1 2 0 -2 1 }} | | {{monzo|-1 2 0 -2 1 }} | ||
|17.58 | | 17.58 | ||
|Loruru | | Loruru | ||
|Mothwellsma | | Mothwellsma | ||
|- | |- | ||
|11 | | 11 | ||
|[[100/99]] | | [[100/99]] | ||
| | | {{monzo| 2 -2 2 0 -1 }} | ||
{{monzo| 2 -2 2 0 -1 }} | | 17.40 | ||
|17.40 | | Luyoyo | ||
|Luyoyo | | Ptolemisma | ||
|Ptolemisma | |||
|- | |- | ||
|11 | | 11 | ||
|[[121/120]] | | [[121/120]] | ||
| | | {{monzo|-3 -1 -1 0 2 }} | ||
{{monzo|-3 -1 -1 0 2 }} | | 14.37 | ||
|14.37 | | Lologu | ||
|Lologu | | Biyatisma | ||
|Biyatisma | |||
|- | |- | ||
|11 | | 11 | ||
|[[176/175]] | | [[176/175]] | ||
|{{monzo| 4 0 -2 -1 1 }} | | {{monzo| 4 0 -2 -1 1 }} | ||
|9.86 | | 9.86 | ||
|Lorugugu | | Lorugugu | ||
|Valinorsma | | Valinorsma | ||
|- | |- | ||
|11 | | 11 | ||
|[[896/891]] | | [[896/891]] | ||
|{{monzo| 7 -4 0 1 -1 }} | | {{monzo| 7 -4 0 1 -1 }} | ||
|9.69 | | 9.69 | ||
|Saluzo | | Saluzo | ||
|Pentacircle comma | | Pentacircle comma | ||
|- | |- | ||
|11 | | 11 | ||
|[[65536/65219]] | | [[65536/65219]] | ||
|{{monzo| 16 0 0 -2 -3 }} | | {{monzo| 16 0 0 -2 -3 }} | ||
|8.39 | | 8.39 | ||
|Satrilu-aruru | | Satrilu-aruru | ||
|Orgonisma | | Orgonisma | ||
|- | |- | ||
|11 | | 11 | ||
|[[385/384]] | | [[385/384]] | ||
| {{monzo|-7 -1 1 1 1 }} | | {{monzo|-7 -1 1 1 1 }} | ||
|4.50 | | 4.50 | ||
|Lozoyo | | Lozoyo | ||
|Keenanisma | | Keenanisma | ||
|- | |- | ||
|11 | | 11 | ||
|[[540/539]] | | [[540/539]] | ||
|{{monzo| 2 3 1 -2 -1 }} | | {{monzo| 2 3 1 -2 -1 }} | ||
|3.21 | | 3.21 | ||
|Lururuyo | | Lururuyo | ||
|Swetisma | | Swetisma | ||
|- | |- | ||
|11 | | 11 | ||
|[[4000/3993]] | | [[4000/3993]] | ||
| | | {{monzo| 5 -1 3 0 -3 }} | ||
{{monzo| 5 -1 3 0 -3 }} | | 3.03 | ||
|3.03 | | Triluyo | ||
|Triluyo | | Wizardharry comma | ||
|Wizardharry comma | |||
|- | |- | ||
|11 | | 11 | ||
|[[9801/9800]] | | [[9801/9800]] | ||
|{{monzo|-3 4 -2 -2 2 }} | | {{monzo|-3 4 -2 -2 2 }} | ||
|0.18 | | 0.18 | ||
| Bilorugu | | Bilorugu | ||
| Kalisma | | Kalisma | ||
|- | |- | ||
|13 | | 13 | ||
|[[65/64]] | | [[65/64]] | ||
|{{monzo|-6 0 1 0 0 1 }} | | {{monzo|-6 0 1 0 0 1 }} | ||
|26.84 | | 26.84 | ||
|Thoyo | | Thoyo | ||
|Wilsorma | | Wilsorma | ||
|- | |- | ||
|13 | | 13 | ||
|[[78/77]] | | [[78/77]] | ||
|{{monzo| 1 1 0 -1 -1 1 }} | | {{monzo| 1 1 0 -1 -1 1 }} | ||
|22.34 | | 22.34 | ||
| Tholuru | | Tholuru | ||
|Negustma | | Negustma | ||
|- | |- | ||
|13 | | 13 | ||
|[[91/90]] | | [[91/90]] | ||
|{{monzo|-1 -2 -1 1 0 1 }} | | {{monzo|-1 -2 -1 1 0 1 }} | ||
| 19.13 | | 19.13 | ||
|Thozogu | | Thozogu | ||
|Superleap comma, biome comma | | Superleap comma, biome comma | ||
|- | |- | ||
| 13 | | 13 | ||
|[[31213/31104]] | | [[31213/31104]] | ||
|{{monzo|-7 -5 0 4 0 1 }} | | {{monzo|-7 -5 0 4 0 1 }} | ||
|6.06 | | 6.06 | ||
|Thoquadzo | | Thoquadzo | ||
|Praveensma | | Praveensma | ||
|- | |- | ||
|31 | | 31 | ||
| [[125/124]] | | [[125/124]] | ||
|{{monzo|-2 0 3 0 0 0 0 0 0 0 -1 }} | | {{monzo|-2 0 3 0 0 0 0 0 0 0 -1 }} | ||
|13.91 | | 13.91 | ||
|Thiwutriyo | | Thiwutriyo | ||
|Twizzler comma | | Twizzler comma | ||
|} | |} | ||
=== Rank-2 temperaments=== | === Rank-2 temperaments === | ||
*[[List of 22et rank two temperaments by badness]] | * [[List of 22et rank two temperaments by badness]] | ||
*[[List of 22et rank two temperaments by complexity]] | * [[List of 22et rank two temperaments by complexity]] | ||
*[[List of edo-distinct 22et rank two temperaments]] | * [[List of edo-distinct 22et rank two temperaments]] | ||
{| class="wikitable center-1 center-2" | {| class="wikitable center-1 center-2" | ||
|- | |- | ||
!Periods<br>per 8ve | ! Periods<br>per 8ve | ||
! Generator | ! Generator | ||
!Temperaments | ! Temperaments | ||
|- | |- | ||
|1 | | 1 | ||
|1\22 | | 1\22 | ||
|[[Escapade]] / [[escaped]]<br>[[Chromo]]<br>[[Ceratitid]] | | [[Escapade]] / [[escaped]]<br>[[Chromo]]<br>[[Ceratitid]] | ||
|- | |- | ||
| 1 | | 1 | ||
|3\22 | | 3\22 | ||
| [[Porcupine]] | | [[Porcupine]] | ||
|- | |- | ||
|1 | | 1 | ||
|5\22 | | 5\22 | ||
|[[Orwell]] (22) / blair (22) / winston (22f) | | [[Orwell]] (22) / blair (22) / winston (22f) | ||
|- | |- | ||
|1 | | 1 | ||
|7\22 | | 7\22 | ||
|[[Magic]] / telepathy | | [[Magic]] / telepathy | ||
|- | |- | ||
|1 | | 1 | ||
|9\22 | | 9\22 | ||
|[[Superpyth]] / [[suprapyth]] | | [[Superpyth]] / [[suprapyth]] | ||
|- | |- | ||
|2 | | 2 | ||
|1\22 | | 1\22 | ||
|[[Shrutar]] / hemipaj<br>[[Comic]] | | [[Shrutar]] / hemipaj<br>[[Comic]] | ||
|- | |- | ||
|2 | | 2 | ||
|2\22 | | 2\22 | ||
|[[Srutal]] / [[pajara]] / pajarous | | [[Srutal]] / [[pajara]] / pajarous | ||
|- | |- | ||
|2 | | 2 | ||
|3\22 | | 3\22 | ||
| | | [[Hedgehog]] / [[echidna]] | ||
[[Hedgehog]] / [[echidna]] | |||
|- | |- | ||
|2 | | 2 | ||
|4\22 | | 4\22 | ||
|[[Astrology]]<br>[[Antikythera]]<br>[[Wizard]] | | [[Astrology]]<br>[[Antikythera]]<br>[[Wizard]] | ||
|- | |- | ||
|2 | | 2 | ||
|5\22 | | 5\22 | ||
|[[Doublewide]] / fleetwood | | [[Doublewide]] / fleetwood | ||
|- | |- | ||
|11 | | 11 | ||
|1\22 | | 1\22 | ||
|[[Undeka]]<br>[[Hendecatonic]] | | [[Undeka]]<br>[[Hendecatonic]] | ||
|} | |} | ||
==Scales== | == Scales == | ||
''See [[22edo modes]]''. | ''See [[22edo modes]]''. | ||
==Tetrachords== | == Tetrachords == | ||
''See [[22edo tetrachords]].'' | ''See [[22edo tetrachords]].'' | ||
==Chord names == | == Chord names == | ||
Combining ups and downs notation with [[color notation]], qualities can be loosely associated with colors: | Combining ups and downs notation with [[color notation]], qualities can be loosely associated with colors: | ||
{| class="wikitable center-all" | {| class="wikitable center-all" | ||
|- | |- | ||
!Quality | ! Quality | ||
![[Color name]] | ! [[Color name]] | ||
![[Monzo]] Format | ! [[Monzo]] Format | ||
! Examples | ! Examples | ||
|- | |- | ||
| rowspan="2" |minor | | rowspan="2" | minor | ||
| zo | | zo | ||
|{{monzo| a b 0 1 }} | | {{monzo| a b 0 1 }} | ||
| 7/6, 7/4 | | 7/6, 7/4 | ||
|- | |- | ||
|fourthward wa | | fourthward wa | ||
|{{monzo| a b }} where b < −1 | | {{monzo| a b }} where b < −1 | ||
| 32/27, 16/9 | | 32/27, 16/9 | ||
|- | |- | ||
| upminor | | upminor | ||
|gu | | gu | ||
|{{monzo| a b -1 }} | | {{monzo| a b -1 }} | ||
|6/5, 9/5 | | 6/5, 9/5 | ||
|- | |- | ||
|downmajor | | downmajor | ||
|yo | | yo | ||
|{{monzo| a b 1 }} | | {{monzo| a b 1 }} | ||
|5/4, 5/3 | | 5/4, 5/3 | ||
|- | |- | ||
| rowspan="2" |major | | rowspan="2" | major | ||
|fifthward wa | | fifthward wa | ||
|{{monzo| a b }} where b > 1 | | {{monzo| a b }} where b > 1 | ||
|9/8, 27/16 | | 9/8, 27/16 | ||
|- | |- | ||
|ru | | ru | ||
| {{monzo| a b 0 -1 }} | | {{monzo| a b 0 -1 }} | ||
|9/7, 12/7 | | 9/7, 12/7 | ||
|} | |} | ||
| Line 1,473: | Line 1,455: | ||
{| class="wikitable center-all" | {| class="wikitable center-all" | ||
|- | |- | ||
![[Kite's color notation|Color of the 3rd]] | ! [[Kite's color notation|Color of the 3rd]] | ||
!JI Chord | ! JI Chord | ||
!Notes as edosteps | ! Notes as edosteps | ||
! Notes of C chord | ! Notes of C chord | ||
!Written name | ! Written name | ||
! Spoken name | ! Spoken name | ||
|- | |- | ||
|zo | | zo | ||
|6:7:9 | | 6:7:9 | ||
| 0-5-13 | | 0-5-13 | ||
|C Eb G | | C Eb G | ||
|Cm | | Cm | ||
|C minor | | C minor | ||
|- | |- | ||
| gu | | gu | ||
|10:12:15 | | 10:12:15 | ||
|0-6-13 | | 0-6-13 | ||
|C ^Eb G | | C ^Eb G | ||
|C^m | | C^m | ||
|C upminor | | C upminor | ||
|- | |- | ||
|yo | | yo | ||
|4:5:6 | | 4:5:6 | ||
|0-7-13 | | 0-7-13 | ||
| C vE G | | C vE G | ||
|Cv | | Cv | ||
|C downmajor or C down | | C downmajor or C down | ||
|- | |- | ||
|ru | | ru | ||
|14:18:21 | | 14:18:21 | ||
|0-8-13 | | 0-8-13 | ||
|C E G | | C E G | ||
| C | | C | ||
| C major or C | | C major or C | ||
| Line 1,511: | Line 1,493: | ||
Examples: | Examples: | ||
*0-4-13 = C D G = C2 | * 0-4-13 = C D G = C2 | ||
* 0-9-13 = C F G = C4 | * 0-9-13 = C F G = C4 | ||
* 0-10-13 = C ^F G = C^4 or C(^4) | * 0-10-13 = C ^F G = C^4 or C(^4) | ||
*0-5-10 = C Eb Gb = Cd = Cdim | * 0-5-10 = C Eb Gb = Cd = Cdim | ||
*0-5-11 = C Eb ^Gb = Cd(^5) | * 0-5-11 = C Eb ^Gb = Cd(^5) | ||
*0-5-12 = C Eb vG = Cm(v5) | * 0-5-12 = C Eb vG = Cm(v5) | ||
Further discussion of 22edo chord naming: | Further discussion of 22edo chord naming: | ||
*[[22edo Chord Names]] | * [[22edo Chord Names]] | ||
*[[22 EDO Chords]] | * [[22 EDO Chords]] | ||
*[[Ups and Downs Notation #Chords and Chord Progressions]] | * [[Ups and Downs Notation #Chords and Chord Progressions]] | ||
*[[Chords of orwell]] | * [[Chords of orwell]] | ||
==Instruments== | == Instruments == | ||
=== Keyboards=== | === Keyboards === | ||
[[File:22-tone halberstadt layout.png|link=https://en.xen.wiki/w/File:22-tone%20halberstadt%20layout.png|alt=|frameless]] | [[File:22-tone halberstadt layout.png|link=https://en.xen.wiki/w/File:22-tone%20halberstadt%20layout.png|alt=|frameless]] | ||
A potential layout for a 22edo keyboard with both split black and white keys. | A potential layout for a 22edo keyboard with both split black and white keys. | ||
==Music == | == Music == | ||
{{Main| 22edo/Music }} | {{Main| 22edo/Music }} | ||
{{Catrel|22edo tracks}} | {{Catrel|22edo tracks}} | ||
==Related pages== | == Related pages == | ||
*[[Lumatone mapping for 22edo]] | * [[Lumatone mapping for 22edo]] | ||
*[[List of MOS scales in 22edo]] | * [[List of MOS scales in 22edo]] | ||
===Approaches=== | === Approaches === | ||
*[[User:Unque/22edo Composition Theory|Unque's approach]] | * [[User:Unque/22edo Composition Theory|Unque's approach]] | ||
*[[William Lynch's thoughts on septimal harmony and 22edo|William Lynch's approach]] | * [[William Lynch's thoughts on septimal harmony and 22edo|William Lynch's approach]] | ||
*[[22edo/Eliora's approach|Eliora's approach]] | * [[22edo/Eliora's approach|Eliora's approach]] | ||
==Further reading== | == Further reading == | ||
*[[Sword, Ron]]. ''[http://www.metatonalmusic.com/books.html Icosakaidiphonic Scales for Guitar: Scales, Chord-Scales, Notation, and Theory for the Twenty-two Equal Divisions of the Octave]''. 2011. | * [[Sword, Ron]]. ''[http://www.metatonalmusic.com/books.html Icosakaidiphonic Scales for Guitar: Scales, Chord-Scales, Notation, and Theory for the Twenty-two Equal Divisions of the Octave]''. 2011. | ||
*[http://lumma.org/tuning/erlich/erlich-decatonic.pdf Erlich, Paul, ''Tuning, Tonality, and Twenty-Two Tone Temperament''] | * [http://lumma.org/tuning/erlich/erlich-decatonic.pdf Erlich, Paul, ''Tuning, Tonality, and Twenty-Two Tone Temperament''] | ||
*[http://porcupinemusic.weebly.com/ "Porcupine Music" - Website Focused on the Development of 22 EDO music] | * [http://porcupinemusic.weebly.com/ "Porcupine Music" - Website Focused on the Development of 22 EDO music] | ||
*[https://docs.google.com/spreadsheets/d/1vnZJTEGOG4FhnGyOwXdpo1KHg73e0KwzgtgbayhT4y0/edit?usp=sharing 11-limit comma lists of selected microtonal EDOs] | * [https://docs.google.com/spreadsheets/d/1vnZJTEGOG4FhnGyOwXdpo1KHg73e0KwzgtgbayhT4y0/edit?usp=sharing 11-limit comma lists of selected microtonal EDOs] | ||
*[https://www.youtube.com/playlist?list=PLWl3gB1BGAwX4sPnbFc5L3gU_IoyUDQ9V Joseph Monzo's visualizations of 22edo scale generation from temperaments] | * [https://www.youtube.com/playlist?list=PLWl3gB1BGAwX4sPnbFc5L3gU_IoyUDQ9V Joseph Monzo's visualizations of 22edo scale generation from temperaments] | ||
== Notes== | == Notes == | ||
<references group="note" /> | <references group="note" /> | ||
==References == | == References == | ||
#Barbour, James Murray, ''Tuning and temperament, a historical survey'', East Lansing, Michigan State College Press, 1953 [c1951] | # Barbour, James Murray, ''Tuning and temperament, a historical survey'', East Lansing, Michigan State College Press, 1953 [c1951] | ||
#Bosanquet, R.H.M. [https://www.webcitation.org/5kjJcrhEx ''On the Hindoo division of the octave, with additions to the theory of higher orders''], Proceedings of the Royal Society of London vol. 26, 1879, pp. 272-284. Reproduced in Tagore, Sourindro Mohun, ''Hindu Music from Various Authors'', Chowkhamba Sanskrit Series, Varanasi, India, 1965 | # Bosanquet, R.H.M. [https://www.webcitation.org/5kjJcrhEx ''On the Hindoo division of the octave, with additions to the theory of higher orders''], Proceedings of the Royal Society of London vol. 26, 1879, pp. 272-284. Reproduced in Tagore, Sourindro Mohun, ''Hindu Music from Various Authors'', Chowkhamba Sanskrit Series, Varanasi, India, 1965 | ||
[[Category:Twentuning]] | [[Category:Twentuning]] | ||
Revision as of 10:12, 13 February 2025
| ← 21edo | 22edo | 23edo → |
Template:EDO intro Because it distinguishes 10/9 and 9/8, it is not a meantone system.
Theory
History
The idea of dividing the octave into 22 steps of equal size seems to have originated with nineteenth century music theorist R. H. M. Bosanquet. Inspired by the division of the octave into 22 unequal parts in the music theory of India, Bosanquet noted that such an equal division was capable of representing 5-limit music with tolerable accuracy. In this he was followed in the twentieth century by theorist José Würschmidt, who noted it as a possible next step after 19edo, and J. Murray Barbour in his classic survey of tuning history, Tuning and Temperament.
Overview to JI approximation quality
The 22edo system is in fact the third equal division, after 12 and 19, which is capable of approximating the 5-limit to within a Tenney–Euclidean error of 4 cents per octave. While not an integral or gap edo it at least qualifies as a zeta peak. Moreover, there is more to it than just the 5-limit; unlike 12 or 19, it is able to approximate the 7- and 11-limit to within 3 cents/oct of error. While 31edo does much better, 22edo still allows the use of these higher-limit harmonies, and in fact 22 is the smallest equal division of the octave to represent the 11-odd-limit consistently. Furthermore, 22edo, unlike 12 and 19, is not a meantone system. The net effect is that 22 allows, and to some extent even forces, the exploration of less familiar musical territory, yet is small enough that it can be used in live performances with suitably designed instruments, like 22-tone guitars.
22edo can also be treated as adding harmonics 3 and 5 to 11edo's 2.9.15.7.11.17 subgroup, making it a rather accurate 2.3.5.7.11.17 subgroup temperament. Let us also mind its approximation of the 31st harmonic is within half a cent, which is very accurate. It also approximates some intervals involving the 29th harmonic well, especially 29/24, which is also matched within half a cent. This leaves us with 2.3.5.7.11.17.29.31.
Since 22edo's fifth is sharp of just by approximately one-quarter of the septimal comma (64/63), and since it tunes the septimal supermajor third (9/7) almost exactly just, it can be treated, for all practical purposes, as an extended "quarter-comma superpyth", in the same way that 31edo can be treated as an extended quarter-comma meantone.
22edo is also the third-smallest edo (after 10edo and 15edo) that maintains 25% or lower relative error on all of the first eight harmonics of the harmonic series.
Prime harmonics
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.0 | +7.1 | -4.5 | +13.0 | -5.9 | -22.3 | +4.1 | -24.8 | +26.3 | +6.8 | +0.4 |
| Relative (%) | +0.0 | +13.1 | -8.2 | +23.8 | -10.7 | -41.0 | +7.6 | -45.4 | +48.2 | +12.4 | +0.8 | |
| Steps (reduced) |
22 (0) |
35 (13) |
51 (7) |
62 (18) |
76 (10) |
81 (15) |
90 (2) |
93 (5) |
100 (12) |
107 (19) |
109 (21) | |
Subsets and supersets
As 22 is divisible by 11, a 22edo instrument can play any music in 11edo, in the same way that 12edo can play 6edo (the whole tone scale). 11edo is interesting for sounding melodically very similar to 12edo (whole steps, half steps and minor thirds in the familiar 1:2:3 ratio), but harmonically very different, in particular because it lacks perfect fifths/fourths and 5-limit major thirds/minor sixths. Similarly, 22edo is melodically similar to 24edo as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In Sagittal notation, 11 can be notated as every other note of 22.
Intervals
| Degree | Cents | Approximate Ratios[note 1] | Ups and downs notation (EUs: v3A1 and ^^d2) |
SKULO notation (K = 1) | Audio | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1/1 | perfect unison | P1 | D | perfect unison | P1 | D | |
| 1 | 54.5 | 36/35, 34/33, 33/32, 32/31 | up-unison, minor 2nd | ^1, m2 | ^D, Eb | comma-wide unison, minor 2nd | K1, m2 | KD, Eb | |
| 2 | 109.1 | 18/17, 17/16, 16/15, 15/14 | downaug 1sn, upminor 2nd | vA1, ^m2 | vD#, ^Eb | classic minor 2nd | Km2 | KEb | |
| 3 | 163.6 | 12/11, 11/10, 10/9 | aug 1sn, downmajor 2nd | A1, vM2 | D#, vE | classic/comma-narrow major 2nd | kM2 | kE | |
| 4 | 218.2 | 9/8, 17/15, 8/7 | major 2nd | M2 | E | major 2nd | M2 | E | |
| 5 | 272.7 | 20/17, 7/6 | minor 3rd | m3 | F | minor 3rd | m3 | F | |
| 6 | 327.3 | 6/5, 17/14, 11/9 | upminor 3rd | ^m3 | ^F | classic minor 3rd | Km3 | KF | |
| 7 | 381.8 | 5/4, 96/77 | downmajor 3rd | vM3 | vF# | classic major 3rd | kM3 | kF# | |
| 8 | 436.4 | 14/11, 9/7, 22/17 | major 3rd | M3 | F# | major 3rd | M3 | F# | |
| 9 | 490.9 | 4/3 | perfect 4th | P4 | G | perfect 4th | P4 | G | |
| 10 | 545.5 | 15/11, 11/8 | up-4th, dim 5th | ^4, d5 | ^G, Ab | comma-wide 4th | K4 | KG | |
| 11 | 600.0 | 7/5, 24/17, 17/12, 10/7 | downaug 4th, updim 5th | vA4, ^d5 | vG#, ^Ab | comma-narrow augmented 4th comma-wide diminished 5th |
kA4 Kd5 |
kG#, KAb | |
| 12 | 654.5 | 16/11, 22/15 | aug 4th, down-5th | A4, v5 | G#, vA | comma-narrow 5th | k5 | kA | |
| 13 | 709.1 | 3/2 | perfect 5th | P5 | A | perfect 5th | P5 | A | |
| 14 | 763.6 | 17/11, 14/9, 11/7 | minor 6th | m6 | Bb | minor 6th | m6 | Bb | |
| 15 | 818.2 | 8/5, 77/48 | upminor 6th | ^m6 | ^Bb | classic minor 6th | Km6 | KBb | |
| 16 | 872.7 | 18/11, 28/17, 5/3 | downmajor 6th | vM6 | vB | classic major 6th | kM6 | kB | |
| 17 | 927.3 | 17/10, 12/7 | major 6th | M6 | B | major 6th | M6 | B | |
| 18 | 981.8 | 7/4, 30/17, 16/9 | minor 7th | m7 | C | minor 7th | m7 | C | |
| 19 | 1036.4 | 9/5, 11/6, 20/11 | upminor 7th, dim 8ve | ^m7, d8 | ^C, Db | classic minor 7th | Km7 | kC | |
| 20 | 1090.9 | 28/15, 15/8, 32/17, 17/9 | downmajor 7th, updim 8ve | vM7, ^d8 | vC#, ^Db | classic major 7th | kM7 | kC# | |
| 21 | 1145.5 | 31/16, 64/33, 33/17, 35/18 | major 7th, down 8ve | M7, v8 | C#, vD | major 7th / comma-narrow 8ve | M7 / k8 | C#, kD | |
| 22 | 1200.0 | 2/1 | perfect octave | P8 | D | perfect 8ve | P8 | D | |
Notation
Ups and downs notation
Spoken as up, downsharp, sharp, upsharp, etc. Note that downsharp can be respelled as dup (double-up), and upflat as dud.
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
||||||
| Flat symbol | |
|
Standard Pythagorean chain-of-fifths notation can be used alongside ups (^) and downs (v), where a single up or down alters the pitch of a note by 1 EDOstep (1\22). Note that E♭ and D♯ are different notes and that E♭ is significantly lower in pitch than D♯.
| Degree | Cents | Ups and Downs Notation | |
|---|---|---|---|
| Diatonic Interval Names | Note Names | ||
| 0 | 0.0 | Perfect unison (P1) | D |
| 1 | 54.5 | Minor second (m2) Up unison (^1) |
Eb ^D |
| 2 | 109.1 | Upminor second (^m2) Downaugmented unison (vA1) Diminished third (d3) |
^Eb vD# Fb |
| 3 | 163.6 | Downmajor second (vM2) Augmented unison (A1) |
vE D# |
| 4 | 218.2 | Major second (M2) Upaugmented unison (^A1) Downminor third (vm3) |
E ^D# vF |
| 5 | 272.7 | Upmajor second (^M2) Minor third (m3) |
^E F |
| 6 | 327.3 | Upminor third (^m3) Diminished fourth (d4) |
^F Gb |
| 7 | 381.8 | Downmajor third (vM3) Augmented second (A2) Updiminished fourth (^d4) |
vF# E# ^Gb |
| 8 | 436.4 | Major third (M3) Upaugmented second (^A2) Down fourth (v4) |
F# ^E# vG |
| 9 | 490.9 | Perfect fourth (P4) | G |
| 10 | 545.5 | Up fourth (^4) Diminished fifth (d5) |
^G Ab |
| 11 | 600.0 | Downaugmented fourth (vA4) Updiminished fifth (^d5) |
vG# ^Ab |
| 12 | 654.5 | Augmented fourth (A4) Down fifth (v5) |
G# vA |
| 13 | 709.1 | Perfect fifth (P5) | A |
| 14 | 763.6 | Up fifth (^5) Minor sixth (m6) |
^A Bb |
| 15 | 818.2 | Downaugmented fifth (vA5) Upminor sixth (^m6) |
vA# ^Bb |
| 16 | 872.7 | Augmented fifth (A5) Downmajor sixth (vM6) |
A# vB |
| 17 | 927.3 | Major sixth (M6) Upaugmented fifth (^A5) Downminor seventh (vm7) |
B ^A# vC |
| 18 | 981.8 | Minor seventh (m7) Upmajor sixth (^M6) Downdiminished octave (vd8) |
C ^B vDb |
| 19 | 1036.4 | Upminor seventh (^m7) Diminished octave (d8) |
^C Db |
| 20 | 1090.9 | Downmajor seventh (vM7) Updiminished octave (^d8) Augmented sixth (A6) |
vC# ^Db B# |
| 21 | 1145.5 | Major seventh (M7) Down octave (v8) |
C# vD |
| 22 | 1200.0 | Perfect octave (P8) | D |
Treating ups and downs as "fused" with sharps and flats, and never appearing separately:
Treating ups and downs as independent of sharps and flats, and sometimes appearing separately:
A D downmajor scale with mandatory accidentals (no key signature), with minimal accidentals (only when needed to override the key signature), and with independent ups and downs.
Alternatively, arrow accidentals from Helmholtz–Ellis notation can be used instead of independent ups and downs:
| Step offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |
|
|
|
|
|
| |
| Flat symbol | |
|
|
|
|
Shown below is Paul Erlich's "Tibia" in G, with independent ups and downs.
Sagittal notation
This notation uses the same sagittal sequence as EDOs 15 and 29, is a subset of the notations for EDOs 44 and 66, and is a superset of the notation for 11-EDO.
Evo flavor

Revo flavor

When 22edo is treated as generated by a cycle of its fifths, the natural notes F C G D A E B represent a chain of those 13\22 fifths; consequently, the whole tone comes out to four degrees and the apotome (Pythagorean sharp/flat) comes out to three degrees. Three pairs of sagittal symbols, dividing that apotome into three parts, are all that is necessary, and offer plenty of enharmonic equivalents:
This notation is consistent with Sagittal's notation of 5-limit JI harmony: "major" 3rds and 6ths appear as (super)pythagorean intervals flattened by a syntonic comma.
The division of the apotome into three syntonic commas also indicates 22's tempering out of the porcupine comma (which is equivalent to three syntonic commas minus a Pythagorean apotome).
We also have, from the appendix to The Sagittal Songbook by Jacob A. Barton, this diagram of how to notate 22-EDO in the Revo flavor of Sagittal:
Superpyth/Porcupine notation
Superpyth/Porcupine notation is a system arising from both superpyth and porcupine temperament. It categorizes each 22edo interval as major and minor of one or both of those temperaments. s indicates superpyth and p indicates porcupine. Because p now represents porcupine and not perfect, P in perfect intervals is no longer used in this system. Instead the number is used without P and is read as either just the number or "Natural". Example: P5 becomes 5 or N5 = Perfect fifth becomes Natural fifth.
Porcupine notation
Porcupine notation uses the porcupine generator to generate the notation as well. The 2nd and 7th are perfect, and the 4th and 5th are imperfect like the 3rd and 6th. The natural notes represent a chain of 2nds ABCDEFG. This is the only way to use a heptatonic notation without additional accidentals.
The keyboard runs D * * E * * F * * G * * * A * * B * * C * * D.
Pentatonic notation
In Pentatonic notation, the degrees are unison, subthird, fourthoid, fifthoid, subseventh and octoid. The natural notes represent a chain of 5ths FCGDA. This is the only way to use a chain-of-fifths notation without additional accidentals.
The keyboard runs D * * * * F * * * G * * * A * * * * C * * * D.
Decatonic notation
The Decatonic notation is based on Paul Erlich's decatonic scales. Unlike typical notation, the decatonic system is based on a scale of 10 tones rather than 7. This approach requires an entire re-learning of chords, intervals, and notation, but it allows 22EDO to be notated using only one pair of accidentals, and gives the opportunity to escape a heptatonic thinking pattern. The system is based on two chains of fifths: one represented by Latin letters, the other by Greek. The two chains can be looked at as two juxtaposed pentatonic scales.
Chain 1: C G D A E
Chain 2: γ δ α ε β
The alphabet is, in ascending order: C δ D ε E γ G α A β C
In this alphabet, a chain of fifths is preserved because equivalent Greek letters also represent fifths if they are the same as their Latin counterparts. For example G–D is a fifth, and so is γ–δ.
Comparison of 22edo notation systems
| Degree | Cents | Superpyth/Porcupine | Porcupine | Pentatonic | Decatonic | Ups and Downs | SKULO interval names | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | Natural Unison | 1 | perfect unison | P1 | D | perfect unison | P1 | D | natural 1st | N1 | C | perfect unison | P1 | D | perfect unison | P1 | D |
| 1 | 55 | s-minor second | sm2 | aug unison | A1 | D# | aug unison | A1 | D# | flat 2nd | f2 | C#, δb | up-unison, minor 2nd | ^1, m2 | ^D, Eb | comma-wide unison, minor 2nd | K1, m2 | KD, Eb |
| 2 | 109 | p-diminished second | pd2 | dim 2nd | d2 | Eb | double-aug unison, double-dim sub3rd |
AA1, dds3 |
Dx, Fb3 |
natural 2nd | N2 | δ | downaug 1sn, upminor 2nd | vA1, ^m2 | vD#, ^Eb | classic minor 2nd | Km2 | KEb |
| 3 | 164 | p-minor second | pm2 | perfect 2nd | P2 | E | dim sub3rd | ds3 | Fbb | sharp 2nd, flat 3rd | s2, f3 | δ#, Db | aug 1sn, downmajor 2nd | A1, vM2 | D#, vE | classic/comma-narrow major 2nd | kM2 | kE |
| 4 | 218 | (s/p) Major second | M2 | aug 2nd | A2 | E# | minor sub3rd | ms3 | Fb | natural 3rd | N3 | D | major 2nd | M2 | E | major 2nd | M2 | E |
| 5 | 273 | s-minor third | sm3 | dim 3rd | d3 | Fb | major sub3rd | Ms3 | F | sharp 3rd | s3 | D# | minor 3rd | m3 | F | minor 3rd | m3 | F |
| 6 | 327 | p-minor third | pm3 | minor 3rd | m3 | F | aug sub3rd | As3 | F# | flat 4th | f4 | εb | upminor 3rd | ^m3 | ^F | classic minor 3rd | Km3 | KF |
| 7 | 382 | p-Major third | pM3 | major 3rd | M3 | F# | double-aug sub3rd, double-dim 4thoid |
AAs3, dd4d |
Fx, Gbb |
natural 4th | N4 | ε | downmajor 3rd | vM3 | vF# | classic major 3rd | kM3 | kF# |
| 8 | 436 | s-Major third | sM3 | aug 3rd, dim 4th | A3, d4 | Fx, Gb | dim 4thoid | d4d | Gb | sharp 4th, flat 5th | s4, f5 | ε#, Eb | major 3rd | M3 | F# | major 3rd | M3 | F# |
| 9 | 491 | Natural Fourth | 4, N4 | minor 4th | m4 | G | perfect 4thoid | P4d | G | natural 5th | N5 | E | perfect 4th | P4 | G | perfect 4th | P4 | G |
| 10 | 545 | p-Major fourth, s-dim fifth | pM4, sd5 | major 4th | M4 | G# | aug 4thoid | A4d | G# | sharp 5th, flat 6th | s5, f6 | E#, γb | up-4th, dim 5th | ^4, d5 | ^G, Ab | comma-wide 4th | K4 | KG |
| 11 | 600 | p-Augmented Fourth, p-diminished Fifth, Half-Octave |
A4, HO | aug 4th, dim 5th |
A4, d5 | Gx, Abb |
double-aug 4thoid, double-dim 5thoid |
AA4d, dd5d |
Gx, Abb |
natural 6th | N6 | γ | downaug 4th, updim 5th | vA4, ^d5 | vG#, ^Ab | comma-narrow augmented 4th comma-wide diminished 5th |
kA4 Kd5 |
kG#, KAb |
| 12 | 655 | p-minor Fifth, s-aug Fourth | pm5, sA4 | minor 5th | m5 | Ab | dim 5thoid | d5d | Ab | sharp 6th, flat 7th | s6, f7 | γ#, Gb | aug 4th, down-5th | A4, v5 | G#, vA | comma-narrow 5th | k5 | kA |
| 13 | 709 | Natural Fifth | 5, N5 | major 5th | M5 | A | perfect 5thoid | P5d | A | natural 7th | N7 | G | perfect 5th | P5 | A | perfect 5th | P5 | A |
| 14 | 764 | s-minor sixth | sm6 | aug 5th, dim 6th | A5, d6 | A#, Bbb | aug 5thoid | A5d | A# | sharp 7th | s7 | G# | minor 6th | m6 | Bb | minor 6th | m6 | Bb |
| 15 | 818 | p-minor sixth | pm6 | minor 6th | m6 | Bb | double-aug 5thoid, double-dim sub7th |
AA5d, dds7 |
Ax, Cb3 |
flat 8th | f8 | αb | upminor 6th | ^m6 | ^Bb | classic minor 6th | Km6 | KBb |
| 16 | 873 | p-Major sixth | pM6 | major 6th | M6 | B | dim sub7th | ds7 | Cbb | natural 8th | N8 | α | downmajor 6th | vM6 | vB | classic major 6th | kM6 | kB |
| 17 | 927 | s-Major sixth | sM6 | aug 6th | A6 | B# | minor sub7th | ms7 | Cb | sharp 8th, flat 9th | s8, f9 | α#, Ab | major 6th | M6 | B | major 6th | M6 | B |
| 18 | 982 | (s/p) minor seventh | m7 | dim 7th | d7 | Cb | major sub7th | Ms7 | C | natural 9th | N9 | A | minor 7th | m7 | C | minor 7th | m7 | C |
| 19 | 1036 | p-Major seventh | pM7 | perfect 7th | P7 | C | aug sub7th | As7 | C# | sharp 9th, flat 10th | s9, f10 | A#, βb | upminor 7th, dim 8ve | ^m7, d8 | ^C, Db | classic minor 7th | Km7 | kC |
| 20 | 1091 | p-Augmented seventh | pA7 | aug 7th | A7 | C# | double-aug sub7th, double-dim octave |
AAs7, dd8 |
Cx, Dbb |
natural 10th | N10 | β | downmajor 7th, updim 8ve | vM7, ^d8 | vC#, ^Db | classic major 7th | kM7 | kC# |
| 21 | 1145 | s-Major seventh | sM7 | dim 8ve | d8 | Db | dim octave | d8 | Db | sharp 10th | s10 | β#, Cb | major 7th, down 8ve | M7, v8 | C#, vD | major 7th / comma-narrow 8ve | M7 / k8 | C#, kD |
| 22 | 1200 | Octave | 8 | perfect octave | P8 | D | perfect octave | P8 | D | natural 11th | N11 | C | perfect octave | P8 | D | perfect 8ve | P8 | D |
Approximation to JI

Interval mappings
The following tables show how 15-odd-limit intervals are represented in 22edo. Prime harmonics are in bold; inconsistent intervals are in italics.
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 9/7, 14/9 | 1.280 | 2.3 |
| 11/10, 20/11 | 1.368 | 2.5 |
| 15/8, 16/15 | 2.640 | 4.8 |
| 5/4, 8/5 | 4.496 | 8.2 |
| 7/6, 12/7 | 5.856 | 10.7 |
| 11/8, 16/11 | 5.863 | 10.7 |
| 3/2, 4/3 | 7.136 | 13.1 |
| 15/11, 22/15 | 8.504 | 15.6 |
| 15/14, 28/15 | 10.352 | 19.0 |
| 5/3, 6/5 | 11.631 | 21.3 |
| 7/4, 8/7 | 12.992 | 23.8 |
| 11/6, 12/11 | 12.999 | 23.8 |
| 9/8, 16/9 | 14.272 | 26.2 |
| 13/11, 22/13 | 16.482 | 30.2 |
| 7/5, 10/7 | 17.488 | 32.1 |
| 13/10, 20/13 | 17.850 | 32.7 |
| 13/9, 18/13 | 17.928 | 32.9 |
| 9/5, 10/9 | 18.767 | 34.4 |
| 11/7, 14/11 | 18.856 | 34.6 |
| 13/7, 14/13 | 19.207 | 35.2 |
| 11/9, 18/11 | 20.135 | 36.9 |
| 13/8, 16/13 | 22.346 | 41.0 |
| 15/13, 26/15 | 24.986 | 45.8 |
| 13/12, 24/13 | 25.064 | 46.0 |
| Interval and complement | Error (abs, ¢) | Error (rel, %) |
|---|---|---|
| 1/1, 2/1 | 0.000 | 0.0 |
| 9/7, 14/9 | 1.280 | 2.3 |
| 11/10, 20/11 | 1.368 | 2.5 |
| 15/8, 16/15 | 2.640 | 4.8 |
| 5/4, 8/5 | 4.496 | 8.2 |
| 7/6, 12/7 | 5.856 | 10.7 |
| 11/8, 16/11 | 5.863 | 10.7 |
| 3/2, 4/3 | 7.136 | 13.1 |
| 15/11, 22/15 | 8.504 | 15.6 |
| 15/14, 28/15 | 10.352 | 19.0 |
| 5/3, 6/5 | 11.631 | 21.3 |
| 7/4, 8/7 | 12.992 | 23.8 |
| 11/6, 12/11 | 12.999 | 23.8 |
| 9/8, 16/9 | 14.272 | 26.2 |
| 13/11, 22/13 | 16.482 | 30.2 |
| 7/5, 10/7 | 17.488 | 32.1 |
| 13/10, 20/13 | 17.850 | 32.7 |
| 9/5, 10/9 | 18.767 | 34.4 |
| 11/7, 14/11 | 18.856 | 34.6 |
| 11/9, 18/11 | 20.135 | 36.9 |
| 13/8, 16/13 | 22.346 | 41.0 |
| 15/13, 26/15 | 24.986 | 45.8 |
| 13/12, 24/13 | 29.482 | 54.0 |
| 13/7, 14/13 | 35.338 | 64.8 |
| 13/9, 18/13 | 36.618 | 67.1 |
Zeta peak index
| Tuning | Strength | Closest edo | Integer limit | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ZPI | Steps per octave | Step size (cents) | Height | Integral | Gap | Edo | Octave (cents) | Consistent | Distinct |
| 80zpi | 22.0251467420146 | 54.4831784348982 | 6.062600 | 1.258178 | 16.213941 | 22edo | 1198.62992556776 | 12 | 8 |
Defining features
Septimal vs. syntonic comma
Possibly the most striking characteristic of 22edo to those not used to it is that it does not temper out the syntonic comma of 81/80. This means that 22 is not a system of meantone temperament, and as such it distinguishes a number of 3-limit and 5-limit intervals that meantone tunings (most notably 12edo, 19edo, 31edo, and 43edo) do not distinguish, such as the two whole tones of 9/8 and 10/9. Indeed, these distinctions are significantly exaggerated in 22edo and 27edo in comparison to 5-limit JI and many more accurate temperaments such as 34edo, 41edo, and 53edo, allowing many opportunities for alternate interpretations of their harmony.
The diatonic scale it produces is instead derived from superpyth temperament. Despite having the same melodic structure as meantone's diatonic scale (LLsLLLs or, 5L 2s), superpyth's diatonic scale has subminor and supermajor thirds of 7/6 and 9/7, rather than minor and major thirds of 6/5 and 5/4. This means that the septimal comma of 64/63 is tempered out, rather than the syntonic comma of 81/80, one of 22et's core features. Superpyth is melodically interesting in that intervals such as A–G♮ and C–B♭ are harmonic sevenths instead of 5-limit minor sevenths (approximately 7/4 instead of 9/5), in addition to having a quasi-equal pentatonic scale (as the major whole tone and subminor third are rather close in size) and more uneven diatonic scale, as compared with 12et and other meantone systems; the step patterns in 22et are 4 – 4 – 5 – 4 – 5 and 4 – 4 – 1 – 4 – 4 – 4 – 1, respectively.
Porcupine comma
It additionally tempers out the porcupine comma or maximal diesis of 250/243, which means that 22edo supports porcupine temperament. The generator for porcupine is a very flat minor whole tone of ~10/9 (usually tuned slightly flat of 11/10), two of which is a sharp ~6/5, and three of which is a slightly flat ~4/3, implying the existence of an equal-step tetrachord, which is characteristic of porcupine. It can be observed that the tuning damage that porcupine tempering implies (the ones just described) is highly characteristic of the tuning properties of 22edo and as such represents one excellent point of departure for examining the harmonic properties of 22edo. It forms mos scales of 7 and 8, which in 22edo are tuned respectively as 4 – 3 – 3 – 3 – 3 – 3 – 3 and 1 – 3 – 3 – 3 – 3 – 3 – 3 – 3 (and their respective modes).
5-limit commas
Other 5-limit commas 22edo tempers out include the diaschisma, 2048/2025 and the magic comma or small diesis, 3125/3072. In a diaschismic system, such as 12et or 22et, the diatonic tritone 45/32, which is a major third above a major whole tone representing 9/8, is equated to its inverted form, 64/45. That the magic comma is tempered out means that 22et is a magic system, where five major thirds make up a perfect fifth.
7-limit commas
In the 7-limit 22edo tempers out certain commas also tempered out by 12et; this relates 12et to 22 in a way different from the way in which meantone systems are akin to it. 50/49 (the jubilisma), and 64/63 (the septimal comma) are tempered out in both systems, so they both equate the two septimal tritones of 7/5 and 10/7, and because of 64/63 the dominant seventh chord and an otonal tetrad are represented by the same chord. Hence both also temper out (50/49)/(64/63) = 225/224, the septimal kleisma, so that the septimal kleisma augmented triad is a chord of 22et, as it also is of any meantone tuning. A septimal comma not tempered out by 12et which 22et does temper out is 1728/1715, the orwell comma; and the orwell tetrad is also a chord of 22et.
11-limit commas
In the 11-limit, 22edo tempers out the quartisma, leading to a stack of five 33/32 quartertones being equated with one 7/6 subminor third. This is a trait which, while shared with 24edo, is surprisingly not shared with a number of other relatively small edos such as 17edo, 26edo and 34edo. In fact, not even the famous 53edo has this property—although it should be noted that the related 159edo does.
Other features
The 163.6¢ "flat minor whole tone" is a key interval in 22edo, in part because it functions as no less than three different consonant ratios in the 11-limit: 10/9, 11/10, and 12/11. It is thus extremely ambiguous and flexible. The trade-off is that it is very much in the cracks of the 12-equal piano, and so for most 12-equal listeners, it takes some getting used to. Simple translations of 5-limit music into 22edo can sound very different, with a more complex harmonic quality inevitably arising. 22edo does not contain a neutral third but both the 5-limit thirds have a "neutral-like" quality since they are tempered closer together rather than farther apart as in 12edo.
22edo also supports the orwell temperament, which uses the septimal subminor third as a generator (5 degrees) and forms mos scales with step patterns 3 – 2 – 3 – 2 – 3 – 2 – 3 – 2 – 2 and 1 – 2 – 2 – 1 – 2 – 2 – 1 – 2 – 2 – 1 – 2 – 2 – 2. Harmonically, orwell can be tuned more accurately in other temperaments, such as 31edo, 53edo and 84edo. But 22edo orwell has a leg-up on the others melodically, as the large and small steps of orwell[9] are easier to distinguish in 22.
22edo is melodically similar to 24edo as both contain quarter-tones and minor, neutral, and major seconds; but 22edo offers much better all-around harmonies than 24. In Sagittal notation, 11 can be notated as every other note of 22.
Regular temperament properties
| Subgroup | Comma list | Mapping | Optimal 8ve stretch (¢) |
Tuning error | |
|---|---|---|---|---|---|
| Absolute (¢) | Relative (%) | ||||
| 2.3 | [35 -22⟩ | [⟨22 35]] | −2.25 | 2.25 | 4.12 |
| 2.3.5 | 250/243, 2048/2025 | [⟨22 35 51]] | −0.86 | 2.70 | 4.94 |
| 2.3.5.7 | 50/49, 64/63, 245/243 | [⟨22 35 51 62]] | −1.80 | 2.85 | 5.23 |
| 2.3.5.7.11 | 50/49, 55/54, 64/63, 99/98 | [⟨22 35 51 62 76]] | −1.11 | 2.90 | 5.33 |
| 2.3.5.7.11.17 | 50/49, 55/54, 64/63, 85/84, 99/98 | [⟨22 35 51 62 76 90]] | −1.09 | 2.65 | 4.87 |
- 22et is lower in relative error than any previous equal temperaments in the 11-limit. The next equal temperament that does better in this subgroup is 31.
- 22et does best in the 2.3.5.7.11.17 subgroup, and the next equal temperament that does better in this subgroup is 46.
Uniform maps
Lua error in Module:Uniform_map at line 135: Must provide edo if not min or max given..
Commas
22et tempers out the following commas. This assumes the val ⟨22 35 51 62 76 81].
| Prime limit |
Ratio[note 2] | Monzo | Cents | Color name | Name |
|---|---|---|---|---|---|
| 3 | (22 digits) | [35 -22⟩ | 156.98 | Trisawa | 22-comma |
| 5 | 20480/19683 | [12 -9 1⟩ | 68.72 | Sayo | Superpyth comma |
| 5 | 250/243 | [1 -5 3⟩ | 49.17 | Triyo | Porcupine comma |
| 5 | 3125/3072 | [-10 -1 5⟩ | 29.61 | Laquinyo | Magic comma |
| 5 | 2048/2025 | [11 -4 -2⟩ | 19.55 | Sagugu | Diaschisma |
| 5 | (14 digits) | [-21 3 7⟩ | 10.06 | Lasepyo | Semicomma |
| 5 | (20 digits) | [32 -7 -9⟩ | 9.49 | Sasa-tritrigu | Escapade comma |
| 5 | (32 digits) | [-53 10 16⟩ | 0.57 | Quadla-quadquadyo | Kwazy comma |
| 7 | 50/49 | [1 0 2 -2⟩ | 34.98 | Biruyo | Jubilisma |
| 7 | 64/63 | [6 -2 0 -1⟩ | 27.26 | Ru | Septimal comma |
| 7 | 875/864 | [-5 -3 3 1⟩ | 21.90 | Zotriyo | Keema |
| 7 | 2430/2401 | [1 5 1 -4⟩ | 20.79 | Quadru-ayo | Nuwell comma |
| 7 | 245/243 | [0 -5 1 2⟩ | 14.19 | Zozoyo | Sensamagic comma |
| 7 | 1728/1715 | [6 3 -1 -3⟩ | 13.07 | Triru-agu | Orwellisma |
| 7 | 225/224 | [-5 2 2 -1⟩ | 7.71 | Ruyoyo | Marvel comma |
| 7 | 10976/10935 | [5 -7 -1 3⟩ | 6.48 | Trizo-agu | Hemimage comma |
| 7 | 6144/6125 | [11 1 -3 -2⟩ | 5.36 | Saruru-atrigu | Porwell comma |
| 7 | 65625/65536 | [-16 1 5 1⟩ | 2.35 | Lazoquinyo | Horwell comma |
| 7 | (12 digits) | [-6 -8 2 5⟩ | 1.12 | Quinzo-ayoyo | Wizma |
| 11 | 99/98 | [-1 2 0 -2 1⟩ | 17.58 | Loruru | Mothwellsma |
| 11 | 100/99 | [2 -2 2 0 -1⟩ | 17.40 | Luyoyo | Ptolemisma |
| 11 | 121/120 | [-3 -1 -1 0 2⟩ | 14.37 | Lologu | Biyatisma |
| 11 | 176/175 | [4 0 -2 -1 1⟩ | 9.86 | Lorugugu | Valinorsma |
| 11 | 896/891 | [7 -4 0 1 -1⟩ | 9.69 | Saluzo | Pentacircle comma |
| 11 | 65536/65219 | [16 0 0 -2 -3⟩ | 8.39 | Satrilu-aruru | Orgonisma |
| 11 | 385/384 | [-7 -1 1 1 1⟩ | 4.50 | Lozoyo | Keenanisma |
| 11 | 540/539 | [2 3 1 -2 -1⟩ | 3.21 | Lururuyo | Swetisma |
| 11 | 4000/3993 | [5 -1 3 0 -3⟩ | 3.03 | Triluyo | Wizardharry comma |
| 11 | 9801/9800 | [-3 4 -2 -2 2⟩ | 0.18 | Bilorugu | Kalisma |
| 13 | 65/64 | [-6 0 1 0 0 1⟩ | 26.84 | Thoyo | Wilsorma |
| 13 | 78/77 | [1 1 0 -1 -1 1⟩ | 22.34 | Tholuru | Negustma |
| 13 | 91/90 | [-1 -2 -1 1 0 1⟩ | 19.13 | Thozogu | Superleap comma, biome comma |
| 13 | 31213/31104 | [-7 -5 0 4 0 1⟩ | 6.06 | Thoquadzo | Praveensma |
| 31 | 125/124 | [-2 0 3 0 0 0 0 0 0 0 -1⟩ | 13.91 | Thiwutriyo | Twizzler comma |
Rank-2 temperaments
- List of 22et rank two temperaments by badness
- List of 22et rank two temperaments by complexity
- List of edo-distinct 22et rank two temperaments
| Periods per 8ve |
Generator | Temperaments |
|---|---|---|
| 1 | 1\22 | Escapade / escaped Chromo Ceratitid |
| 1 | 3\22 | Porcupine |
| 1 | 5\22 | Orwell (22) / blair (22) / winston (22f) |
| 1 | 7\22 | Magic / telepathy |
| 1 | 9\22 | Superpyth / suprapyth |
| 2 | 1\22 | Shrutar / hemipaj Comic |
| 2 | 2\22 | Srutal / pajara / pajarous |
| 2 | 3\22 | Hedgehog / echidna |
| 2 | 4\22 | Astrology Antikythera Wizard |
| 2 | 5\22 | Doublewide / fleetwood |
| 11 | 1\22 | Undeka Hendecatonic |
Scales
See 22edo modes.
Tetrachords
See 22edo tetrachords.
Chord names
Combining ups and downs notation with color notation, qualities can be loosely associated with colors:
| Quality | Color name | Monzo Format | Examples |
|---|---|---|---|
| minor | zo | [a b 0 1⟩ | 7/6, 7/4 |
| fourthward wa | [a b⟩ where b < −1 | 32/27, 16/9 | |
| upminor | gu | [a b -1⟩ | 6/5, 9/5 |
| downmajor | yo | [a b 1⟩ | 5/4, 5/3 |
| major | fifthward wa | [a b⟩ where b > 1 | 9/8, 27/16 |
| ru | [a b 0 -1⟩ | 9/7, 12/7 |
All 22edo chords can be named using ups and downs. Alterations are always enclosed in parentheses, additions never are. An up or down immediately after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13).Here are the zo, gu, yo and ru triads:
| Color of the 3rd | JI Chord | Notes as edosteps | Notes of C chord | Written name | Spoken name |
|---|---|---|---|---|---|
| zo | 6:7:9 | 0-5-13 | C Eb G | Cm | C minor |
| gu | 10:12:15 | 0-6-13 | C ^Eb G | C^m | C upminor |
| yo | 4:5:6 | 0-7-13 | C vE G | Cv | C downmajor or C down |
| ru | 14:18:21 | 0-8-13 | C E G | C | C major or C |
Examples:
- 0-4-13 = C D G = C2
- 0-9-13 = C F G = C4
- 0-10-13 = C ^F G = C^4 or C(^4)
- 0-5-10 = C Eb Gb = Cd = Cdim
- 0-5-11 = C Eb ^Gb = Cd(^5)
- 0-5-12 = C Eb vG = Cm(v5)
Further discussion of 22edo chord naming:
- 22edo Chord Names
- 22 EDO Chords
- Ups and Downs Notation #Chords and Chord Progressions
- Chords of orwell
Instruments
Keyboards
A potential layout for a 22edo keyboard with both split black and white keys.
Music
- See also: Category:22edo tracks
Related pages
Approaches
Further reading
- Sword, Ron. Icosakaidiphonic Scales for Guitar: Scales, Chord-Scales, Notation, and Theory for the Twenty-two Equal Divisions of the Octave. 2011.
- Erlich, Paul, Tuning, Tonality, and Twenty-Two Tone Temperament
- "Porcupine Music" - Website Focused on the Development of 22 EDO music
- 11-limit comma lists of selected microtonal EDOs
- Joseph Monzo's visualizations of 22edo scale generation from temperaments
Notes
References
- Barbour, James Murray, Tuning and temperament, a historical survey, East Lansing, Michigan State College Press, 1953 [c1951]
- Bosanquet, R.H.M. On the Hindoo division of the octave, with additions to the theory of higher orders, Proceedings of the Royal Society of London vol. 26, 1879, pp. 272-284. Reproduced in Tagore, Sourindro Mohun, Hindu Music from Various Authors, Chowkhamba Sanskrit Series, Varanasi, India, 1965