22edo/Unque's compositional approach
22 Equal Divisions of the Octave is arguably the smallest EDO to support the full 11-limit; it is also the intersection of many popular temperaments such as Superpyth, Porcupine, Orwell, and Magic. Additionally, fans of 15edo will likely be drawn to 22edo due to the latter being quite useful as an extension of the former that represents many low-complexity intervals with higher accuracy. On this page, I will present my personal experience with 22edo, and hopefully provide a potential framework that others may use to begin their own journeys through the colorful world of 22 Equal Divisions of the Octave.
As always, this page will be full of personal touches that may not reflect an objective truth or even wide consensus about how to use 22edo; I encourage learning musicians to experiment with different ideas and develop styles that best suit their own needs, rather than to take my word (or anyone else's for that matter) at face value as a great truth of music.
Intervals
22edo is often regarded as a full 11-limit system or some subgroup thereof; I will here prioritize intervals of the 7-limit, as they better describe the harmony of 22edo, but 11-limit intervals will additionally be used where applicable.
| Interval | Cents | JI Intervals | As a generator | Notation | Notes |
|---|---|---|---|---|---|
| 0\22 | 0 | 1/1 | C | ||
| 1\22 | 54.5 | 36/35, 28/27, 25/24 | Escapade | D♭, A𝄪 | |
| 2\22 | 109.1 | 16/15 | 11edo | B♯, E𝄫 | |
| 3\22 | 163.6 | 10/9 | Porcupine | C♯, F𝄫 | |
| 4\22 | 218.2 | 9/8, 8/7 | Wizard, Jubilic | D | |
| 5\22 | 272.7 | 7/6 | Orwell | E♭, B𝄪 | Often considered less concordant than a true 7/6 |
| 6\22 | 327.3 | 6/5, 11/9 | Doublewide | F♭, C𝄪 | |
| 7\22 | 381.8 | 5/4 | Magic | D♯, G𝄫 | |
| 8\22 | 436.3 | 14/11, 32/25, 9/7 | Sensamagic | E | Sensamagic is inherited from 11edo |
| 9\22 | 490.9 | 21/16, 4/3 | Superpyth | F | |
| 10\22 | 545.5 | 15/11, 11/8 | Joan | G♭, D𝄪 | Joan is inherited from 11edo |
| 11\22 | 600.0 | 7/5, 45/32, 64/45, 10/7 | 2edo; period for several temps | E♯, A𝄫 | |
| 12\22 | 654.5 | 16/11, 22/15 | Joan | F♯ | |
| 13\22 | 709.1 | 3/2, 32/21 | Superpyth | G | |
| 14\22 | 763.6 | 14/9, 25/16, 11/7 | Sensamagic | A♭, E𝄪 | |
| 15\22 | 818.2 | 8/5 | Magic | B𝄫, F𝄪 | Probably better notated with ups and downs (see below) |
| 16\22 | 872.7 | 18/11, 5/3 | Doublewide | G♯, C𝄫 | |
| 17\22 | 927.3 | 12/7 | Orwell | A | |
| 18\22 | 981.8 | 7/4, 16/9 | Wizard, Jubilic | B♭ | |
| 19\22 | 1036.3 | 9/5 | Porcupine | C♭, G𝄪 | |
| 20\22 | 1090.9 | 15/8 | 11edo | A♯, D𝄫 | |
| 21\22 | 1145.5 | 48/25, 27/14, 35/18 | Escapade | B | |
| 22\22 | 1200.0 | 2/1 | C |
The intervals of 22edo can be notated using the familiar Circle of Fifths; additionally, ups and downs notation uses the accidentals ^ and v to modify a given note by one step of 22edo, so that B𝄫 may for instance be more concisely notated as ^A♭ to avoid the potentially confusing double-flat.
The thirds of 22edo
22edo has two pairs of thirds: a major/minor pair, and a supermajor/subminor pair; despite most often being viewed as an 11-limit system, it lacks clear representation for the neutral thirds that are characteristic of 11-limit harmony.
The subminor third at 5\22 represents 7/6 with moderate accuracy, though it is often noted to be significantly less concordant than the JI representation. Its fifth complement is the supermajor third at 8\22, which is an excellent representation of 9/7. This interval is perhaps better paired with 14\22 than with 13\22, as the former can be interpreted as 11/7 and thus provides the more consonant otonal 7:9:11 triad.
The minor third at 6\22 is contentious in its interpretation; it is quite sharp for a minor third, though not nearly sharp enough to constitute a neutral third; by patent val, it represents 6/5 and 11/9, though in practice it does not accurately represent either of the two. Its fifth complement, the major third at 7\22, is a much clearer 5/4, having a relative error of less than 10%.
Scales
5L 2s
The 5L 2s scale is one of two types of Diatonic scales represented in 22edo, and represents the shade of Diatonic popularized by the Greek mathematician Archytas, which uses the 2.3.7 subgroup of Just Intonation. It is generated by the Circle of Fifths just as in common practice tunings, though the perfect fifth of 22edo is significantly sharper than any tuning attested in common practice, which makes the scale and its chords behave somewhat differently from standard Diatonic functionality. Notably, suspended chords feel less tense and more restful, while typical tertian triads tend to sound tenser and more energetic; this is the opposite of how these chords behave in Meantone tunings, and as such Western music translated into 22edo's Diatonic may sound strange if it is not adjusted to account for its unique properties.
| Gens Up | Step Pattern | Notation | Name |
|---|---|---|---|
| 6 | LLLsLLs | C - D - E - F♯ - G - A - B - C | Lydian |
| 5 | LLsLLLs | C - D - E - F - G - A - B - C | Ionian |
| 4 | LLsLLsL | C - D - E - F - G - A - B♭ - C | Mixolydian |
| 3 | LsLLLsL | C - D - E♭ - F - G - A - B♭ - C | Dorian |
| 2 | LsLLsLL | C - D - E♭ - F - G - A♭ - B♭ - C | Aeolian |
| 1 | sLLLsLL | C - D♭ - E♭ - F - G - A♭ - B♭ - C | Phrygian |
| 0 | sLLsLLL | C - D♭ - E♭ - F - G♭ - A♭ - B♭ - C | Locrian |
5L 7s
The 5L 7s scale is an extension of 5L 2s created by continuing the generator sequence. Because the Circle of Fifths is bidirectional, the seven modes can be extended either by continuing the sequence upwards or downwards; those created by going up the chain are called grave modes, and those extended by going down the chain are called acute modes.
| Gens Up | Step Pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 11 | LsLsLssLsLss | C - C♯ - D - D♯ - E - E♯ - F♯ - G - G♯ - A - A♯ - B - C | Grave Lydian | Like the seven-note Lydian, lacks a Perfect Fourth over the root. |
| 10 | LsLssLsLsLss | C - C♯ - D - D♯ - E - F - F♯ - G - G♯ - A - A♯ - B - C | Grave Ionian | |
| 9 | LsLssLsLssLs | C - C♯ - D - D♯ - E - F - F♯ - G - G♯ - A - B♭ - B - C | Grave Mixolydian | |
| 8 | LssLsLsLssLs | C - C♯ - D - E♭ - E - F - F♯ - G - G♯ - A - B♭ - B - C | Grave Dorian | |
| 7 | LssLsLssLsLs | C - C♯ - D - E♭ - E - F - F♯ - G - A♭ - A - B♭ - B - C | Grave Aeolian | |
| 6 | sLsLsLssLsLs | C - D♭ - D - E♭ - E - F - F♯ - G - A♭ - A - B♭ - B - C | Grave Phrygian | Also accounts for Acute Lydian |
| 5 | sLsLssLsLsLs | C - D♭ - D - E♭ - E - F - G♭ - G - A♭ - A - B♭ - B - C | Acute Ionian | Also accounts for Grave Locrian |
| 4 | sLsLssLsLssL | C - D♭ - D - E♭ - E - F - G♭ - G - A♭ - A - B♭ - C♭ - C | Acute Mixolydian | |
| 3 | sLssLsLsLssL | C - D♭ - D - E♭ - F♭ - F - G♭ - G - A♭ - A - B♭ - C♭ - C | Acute Dorian | |
| 2 | sLssLsLssLsL | C - D♭ - D - E♭ - F♭ - F - G♭ - G - A♭ - B𝄫 - B♭ - C♭ - C | Acute Aeolian | |
| 1 | ssLsLsLssLsL | C - D♭ - E𝄫 - E♭ - F♭ - F - G♭ - G - A♭ - B𝄫 - B♭ - C♭ - C | Acute Phrygian | |
| 0 | ssLsLssLsLsL | C - D♭ - E𝄫 - E♭ - F♭ - F - G♭ - A𝄫 - A♭ - B𝄫 - B♭ - C♭ - C | Acute Locrian | Like the seven-note Locrian, lacks a Perfect Fifth over the root. |
3L 2M 2s
The 3L 2M 2s scale is the other type of Diatonic scale represented in 22edo; this one represents the 5-limit shade of Diatonic popularized by musicians and theorists such as Ptolemy and Zarlino. It is generated by alternating intervals 6\22 and 7\22, and as such yields two different forms ("left-hand" and "right-hand") based on which generator comes first and which comes second.
The 5-limit harmony of this scale is much more reminiscent of the familiar harmony used in common-practice music, so popular music translated into this scale will be much more faithful to the harmony of the original piece than it would be using 5L 2s.
| Gens Up | Step pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 6 | LMLsLMs | C - D - vE - vF♯ - G - A - vB - C | Lydian | Tritone is precisely the semioctave |
| 5 | LsLMsLM | C - D - ^E♭ - ^F - G - ^A♭ - ^B♭ - C | Aeolian | Contains the Wolf fourth (^F) |
| 4 | LMsLMLs | C - D - vE - F - G - vA - vB - C | Ionian | |
| 3 | sLMLsLM | C - ^D♭ - ^E♭ - F - G - vA♭ - ^B♭ - C | Phrygian | |
| 2 | MLsLMsL | C - vD - vE - F - G - vA - B♭ - C | Mixolydian | |
| 1 | sLMsLML | C - ^D♭ - ^E♭ - F - ^G♭ - ^A♭ - B♭ - C | Locrian | Tritone is precisely the semioctave |
| 0 | MsLMLsL | C - vD - E♭ - F - vG - vA - B♭ - C | Dorian | Contains the Wolf fifth (vG) |
| Gens Up | Step pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 6 | LsLMLsM | C - D - ^E♭ - ^F - G - A - ^B♭ - C | Dorian | Contains the Wolf fourth (^F) |
| 5 | LMLsMLs | C - D - vE - vF♯ - G - vA - vB - C | Lydian | Tritone is precisely the semioctave |
| 4 | LsMLsLM | C - D - ^E♭ - F - G - ^A♭ - ^B♭ - C | Aeolian | |
| 3 | MLsLMLs | C - vD - vE - F - G - vA - vB - C | Ionian | |
| 2 | sLMLsML | C - ^D♭ - ^E♭ - F - G - ^A♭ - B♭ - C | Phrygian | |
| 1 | MLsMLsL | C - vD - vE - F - vG - vA - B♭ - C | Mixolydian | Contains the Wolf fifth (vG) |
| 0 | sMLsLML | C - ^D♭ - E♭ - F - ^G♭ - ^A♭ - B♭ - C | Locrian | Tritone is precisely the semioctave |
When disambiguation is needed between the modes of 5L 2s and 3L 2M 2s, the former can be described as "Superpyth" or "Archy," while the latter can be called "Nicetone" or "Zarlino"
5L 2m 3s
The 5L 2m 3s scale functions as an extension to 3L 2M 2s, created by adding a commatic step into each large step of that Diatonic scale. This provides the scale with three new modes in addition to the seven already present. Due to the commatic step, this scale does not distinguish the left-hand from the right-hand variants.
While there is no singular generator sequence used to create this scale, it can be thought of as two pentatonic scales offset by a neutral second, which is coincidentally the amount by which a sharp or flat alters a note; this makes the scale easy to notate as a pentatonic scale and its sharp/flat counterpart. This splits the modes into five "grave" modes and five "acute" modes, where the grave modes place the root on the flattened pentatonic, and the acute modes place the root on the sharpened one.
| Gens Up | Step pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 4 | LmLsLmLsLs | C - C♯ - E♭ - E - F - F# - A♭ - A - B♭ - B - C | Aeolian | Contains the Wolf fifth (^G) |
| 3 | LmLsLsLmLs | C - C♯ - E♭ - E - F - F# - G - G♯ - B♭ - B - C | Dorian | |
| 2 | LsLmLsLmLs | C - C♯ - D - D♯ - F - F# - G - G♯ - B♭ - B - C | Mixolydian | |
| 1 | LsLmLsLsLm | C - C♯ - D - D♯ - F - F# - G - G♯ - A - A♯ - C | Ionian | |
| 0 | LsLsLmLsLm | C - C♯ - D - D♯ - E - E♯ - G - G♯ - A - A♯ - C | Lydian | Brightness is reversed - Lydian is the darkest grave mode! |
| Gens Up | Step pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 4 | mLsLmLsLsL | C - E𝄫 - E♭ - F♭ - F - A𝄫 - A♭ - B𝄫 - B♭ - C♭ - C | Locrian | Brightness is reversed - Locrian is the brightest acute mode! |
| 3 | mLsLsLmLsL | C - E𝄫 - E♭ - F♭ - F - G♭ - G - B𝄫 - B♭ - C♭ - C | Phrygian | |
| 2 | sLmLsLmLsL | C - D♭ - D - F♭ - F - G♭ - G - B𝄫 - B♭ - C♭ - C | Aeolian | |
| 1 | sLmLsLsLmL | C - D♭ - D - F♭ - F - G♭ - G - A♭ - A - C♭ - C | Dorian | |
| 0 | sLsLmLsLmL | C - D♭ - D - E♭ - E - G♭ - G - A♭ - A - C♭ - C | Mixolydian | Contains the Wolf fourth (vF) |
Where disambiguation is needed between the modes of 5L 7s and 5L 2M 2s, the former can be described as "chromatic," and the latter as "blackdye."
2L 8s
The 2L 8s scale is another characteristic scale of 22edo, which was discovered independently by Paul Erlich, Gene Ward Smith, and Olivier Messiaen (though the latter theorist documented the scale's analog in 12edo rather than in 22).
This scale is a mode of limited transposition, which means that it has some amount of rotational symmetry. In this case, the semioctave is the axis of symmetry, and transposing a mode up by 11 steps of 22edo (or 6 steps of 12edo in the case of Messiaen's works) yields the same set of pitches as the mode on which you started.
Erlich divides four of the five unique rotations into a 2x2 grid, categorized by how many thirds it contains (one third is "static," two is "dynamic,") and which type of third falls on the fourth degree of the scale (major or minor). The brightest mode does not appear to have been considered by Erlich, due to lacking a perfect fifth above the root.
| Gens Up | Step pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 8 | LssssLssss | C - C♯ - E♭ - vE - F - vF♯ - vF𝄪 - vA - ^A - ^C♭ - C | Wolf Minor | Contains the wolf fifth (^G) |
| 6 | sLssssLsss | C - vC♯ - E♭ - vE - F - vF♯ - ^F♯ - vA - ^A - ^C♭ - C | Dynamic Major | Dual thirds are subminor and major |
| 4 | ssLssssLss | C - vC♯ - vE♭ - vE - F - vF♯ - ^F♯ - ^A♭ - ^A - ^C♭ - C | Static Major | Laterally symmetrical |
| 2 | sssLssssLs | C - vC♯ - vE♭ - ^E♭ - F - vF♯ - ^F♯ - ^A♭ - A - ^C♭ - C | Static Minor | Messiaen treated this rotation as the "default" |
| 0 | ssssLssssL | C - vC♯ - vE♭ - ^E♭ - vF - vF♯ - ^F♯ - ^A♭ - A - C♭ - C | Dynamic Minor | Dual thirds are minor and supermajor |
4L 5s
The 4L 5s scale is another quite useful scale available in 22edo and a perfect example of 22edo being better than 31; it is closely associated with Orwell temperament, and as such is best utilized alongside Orwell Chords for functional harmony (see below).
| Gens Up | Step Pattern | Notation | Notes |
|---|---|---|---|
| 8 | LsLsLsLss | C - C♯ - E♭ - ^D♯ - G♭ - ^F♯ - ^A♭ - ^A - A♯ - C | ^F♯ is actually the Wolf Fifth in this context, and F♯ is the desirable interval! |
| 7 | LsLsLssLs | C - C♯ - E♭ - ^D♯ - G♭ - ^F♯ - ^A♭ - A - A♯ - C | |
| 6 | LsLssLsLs | C - C♯ - E♭ - ^D♯ - G♭ - F♯ - ^A♭ - A - A♯ - C | |
| 5 | LssLsLsLs | C - C♯ - E♭ - D♯ - G♭ - F♯ - ^A♭ - A - A♯ - C | |
| 4 | sLsLsLsLs | C - vC♯ - E♭ - D♯ - G♭ - F♯ - ^A♭ - A - A♯ - C | |
| 3 | sLsLsLssL | C - vC♯ - E♭ - D♯ - G♭ - F♯ - ^A♭ - A - vA♯ - C | |
| 2 | sLsLssLsL | C - vC♯ - E♭ - D♯ - G♭ - F♯ - A♭ - A - vA♯ - C | |
| 1 | sLssLsLsL | C - vC♯ - E♭ - D♯ - vG♭ - F♯ - A♭ - A - vA♯ - C | vG♭ is actually the Wolf Fourth in this context, and G♭ is the desirable interval! |
| 0 | ssLsLsLsL | C - vC♯ - vE♭ - D♯ - vG♭ - F♯ - A♭ - A - vA♯ - C | Subminor third above the root is unavailable in this mode. |
3L 4s
The 3L 4s scale is a distant deviation from common-practice harmony. The harmony in this scale is based primarily on Marvel triads (see below) rather than the typical major and minor triads that the other scales were quite generously accustomed to. It is closely related to Magic temperament, and may be thought of as the functional opposite of the 4L 5s due to their nature as leaning into augmented and diminished harmony respectively as their primary concordances. The modes of 3L 4s are given names by Andrew Heathwaite.
| Gens Up | Step Pattern | Notation | Name | Notes |
|---|---|---|---|---|
| 6 | LsLsLss | C - vD♯ - vE - ^F♯ - ^G - A♯ - B - C | Dril | ^F♯ and ^G both act as fifths, so this mode contains no functional fourths. |
| 5 | LsLssLs | C - vD♯ - vE - ^F♯ - ^G - ^A♭ - B - C | Gil | |
| 4 | LssLsLs | C - vD♯ - vE - vF - ^G - ^A♭ - B - C | Kleeth | |
| 3 | sLsLsLs | C - D♭ - vE - vF - ^G - ^A♭ - B - C | Bish | Contains the up- and down-leading tones, making it easy to root melodically. |
| 2 | sLsLssL | C - D♭ - vE - vF - ^G - ^A♭ - ^B𝄫 - C | Fish | |
| 1 | sLssLsL | C - D♭ - vE - vF - vG♭ - ^A♭ - ^B𝄫 - C | Jwl | vF and vG♭ both act as fourths, so this mode contains no functional fifths. |
| 0 | ssLsLsL | C - D♭ - E𝄫 - vF - vG♭ - ^A♭ - ^B𝄫 - C | Led |
3L 7s
Since the 3L 4s scale can be created by continually stacking Major Thirds, this structure can be extended quite easily into a larger scale that has more options available for harmonic content. This pattern gives us the scale 3L 7s, which was discussed at length in the paper Tractatum de Modi Sephiratorum by Komorsky. In addition to the scale itself, Komorsky provides unique names for all ten rotations of the scale, named for the ten Sefirot of the Kabbalah school of thought; if desired, however, one can also consider the modes to be Grave and Acute extensions of the 3L 4s modes, making the relationships between the two scales clearer.
| Gens Up | Step Pattern | Notation | Name (Komorsky) | Name (Heathwaite) | Notes |
|---|---|---|---|---|---|
| 9 | LssLssLsss | C - vC𝄪 - vD♯ - vE - ^E♯ - ^F♯ - ^G - G𝄪 - A♯ - B - C | Malkuth | Grave Dril | Like Dril, contains no functional fourths |
| 8 | LssLsssLss | C - vC𝄪 - vD♯ - vE - ^E♯ - ^F♯ - ^G - ^A♭ - A♯ - B - C | Yesod | Grave Gil | Like Gil, contains no functional fourths |
| 7 | LsssLssLss | C - vC𝄪 - vD♯ - vE - vF - ^F♯ - ^G - ^A♭ - A♯ - B - C | Hod | Grave Kleeth | |
| 6 | sLssLssLss | C - D♭ - vD♯ - vE - vF - ^F♯ - ^G - ^A♭ - A♯ - B - C | Netzach | Grave Bish | Also accounts for Acute Dril |
| 5 | sLssLsssLs | C - D♭ - vD♯ - vE - vF - ^F♯ - ^G - ^A♭ - ^B𝄫 - B - C | Tiferet | Grave Fish | Also accounts for Acute Gil |
| 4 | sLsssLssLs | C - D♭ - vD♯ - vE - vF - vG♭ - ^G - ^A♭ - ^B𝄫 - B - C | Gevurah | Acute Kleeth | Also accounts for Grave Jwl |
| 3 | ssLssLssLs | C - D♭ - E𝄫 - vE - vF - vG♭ - ^G - ^A♭ - ^B𝄫 - B - C | Chesed | Acute Bish | Also accounts for Grave Led |
| 2 | ssLssLsssL | C - D♭ - E𝄫 - vE - vF - vG♭ - ^G - ^A♭ - ^B𝄫 - ^C𝄫 - C | Binah | Acute Fish | |
| 1 | ssLsssLssL | C - D♭ - E𝄫 - vE - vF - vG♭ - vA𝄫 - ^A♭ - ^B𝄫 - ^C𝄫 - C | Chokmah | Acute Jwl | Like Jwl, contains no functional fifths |
| 0 | sssLssLssL | C - D♭ - E𝄫 - F𝄫 - vF - vG♭ - vA𝄫 - ^A♭ - ^B𝄫 - ^C𝄫 - C | Keter | Acute Led | Like Led, contains no functional fifths |
Chords of 22edo
22edo provides a number of ways to construct and notate chords; while I cannot provide a comprehensive list of every possible chord available in 22edo, I will discuss and generalize the forms that I find to be most important for 22edo's structure.
Tertiary Triads
Having four types of thirds rather than two, 22edo has a more colorful array of tertian triads than common practice music does. The 5-limit Major and Minor triads can be approximated using 6\22 and 7\22 as the thirds, and the 7-limit triads can be approximated using 5\22 and 8\22.
Additionally, there are four distinct types of diminished triads that can be formed using the two types of minor thirds; due to the Marvel comma being tempered out in 22edo, however, there are only two distinct types of augmented triads that can be formed using the two types of major thirds, as 7 + 7 + 8 = 22.
| Name | Symbol | Notation | Formula | Otonal | Utonal | Notes |
|---|---|---|---|---|---|---|
| Major | C maj | C - vE - G | 7\22 + 6\22 | 4:5:6 | 1/(15:12:10) | Primary consonance in 3L 2M 2s |
| Minor | c min | C - ^E♭ - G | 6\22 + 7\22 | 10:12:15 | 1/(6:5:4) | Primary consonance in 3L 2M 2s |
| Supermajor | C saj | C - E - G | 8\22 + 5\22 | 14:18:21 | 1/(9:7:6) | Primary consonance in 5L 2s |
| Subminor | c sin | C - E♭ - G | 5\22 + 8\22 | 6:7:9 | 1/(21:18:14) | Primary consonance in 5L 2s |
| Orwell Dim. | cow | C - E♭ - G♭ | 5\22 + 5\22 | 24:28:33 | 1/(33:28:24) | Primary consonance in 4L 5s |
| Utonal Dim. | cut | C - E♭ - ^G♭ | 5\22 + 6\22 | 30:35:42 | 1/(7:6:5) | |
| Otonal Dim. | cot | C - ^E♭ - ^G♭ | 6\22 + 5\22 | 5:6:7 | 1/(42:35:30) | |
| Orgone Dim. | cog | C - ^E♭ - vG | 6\22 + 6\22 | 25:30:36 | 1/(36:30:25) | Useful consonance in 11edo |
| Minor Wolf | c sv | C - E♭ - vG | 5\22 + 7\22 | 24:28:35 | 1/(35:30:24) | Appears in right-hand 3L 2M 2s |
| Major Wolf | C v | C - E - vG | 7\22 + 5\22 | 24:30:35 | 1/(35:28:24) | Appears in left-hand 3L 2M 2s |
| Marvel | C+ | C - vE - ^G | 7\22 + 7\22 | 16:20:25 | 1/(25:20:16) | Primary consonance in 3L 4s |
| Marvel (1st inv.) | vG♯+/C | C - vE - vG♯ | 7\22 + 8\22 | 20:25:32 | 1/(40:32:25) | |
| Marvel (2nd inv.) | E+/C | C - E - vG♯ | 8\22 + 7\22 | 25:32:40 | 1/(32:25:20) | |
| Sensamagic | C× | C - E - G♯ | 8\22 + 8\22 | 11:14:18 | 1/(18:14:11) | Useful consonance in 11edo |
| Sensa (1st inv.) | ^G×/C | C - E - ^G | 8\22 + 6\22 | 7:9:11 | 1/(14:11:9) | |
| Sensa (2nd inv.) | E♭×/C | C - E♭ - ^G | 6\22 + 8\22 | 9:11:14 | 1/(11:9:7) |
Quartal Inversions
In diatonic tunings with a sharp-tempered 3/2, such as the Superpyth diatonic found in 22edo, quartal harmony is often more concordant than tertian harmony; as such, musicians interested in using Superpyth should familiarize themselves with the Quartal Triad and its inversions.
| Gens Up | Symbol | Notation | Formula | 3-limit JI | 7-limit JI |
|---|---|---|---|---|---|
| 2|0 | C4 | C - F - B♭ | 9\22 + 9\22 | 9:12:16 | 16:21:28 |
| 1|1 | Csus4 | C - F - G | 9\22 + 4\22 | 6:8:9 | 16:21:24 |
| 0|2 | Csus2 | C - D - G | 4\22 + 9\22 | 8:9:12 | 14:16:21 |
Functional Harmony
Useful harmonic progressions may arise in a number of ways depending on the scale being used and depending on what chord the composer wishes to tonicize. Here, I will document some examples of how functional harmonic progressions may be created in the different scales of 22edo, with concepts that can be extended to apply to any scale.
Note that I will be constructing these chord progressions from back to front; this means that we will start with the resolution, then find the dominant chord, and then find a subdominant to precede it.
Elements of Functional Harmony
Just like in common-practice music theory, chords in 22edo have a tendency to rotate about the Circle of Fifths. This means that in Diatonic music and other scales that contain 13\22, the chord built off of that note will be useful as a dominant.
Due to 22edo's smaller step size, there are two types of leading tones. The smaller of the two can be found in the Superpyth Diatonic scale, where it is much tenser than the leading tone found in common-practice music; and the larger of the two is the small step of the Zarlino diatonic scale, which while less tense than the smaller leading tone is more useful as a dissonant chord tone to provide some extra tension.
Finally, it is important to notice certain tense intervals that have a tendency to voice lead by contrary motion to certain other intervals. Specifically, the semioctave has a tendency to resolve either inwards or outwards to yield a perfect fourth/fifth; additionally, the subminor third may resolve outwards to a major third, and the supermajor third may resolve inwards to a minor third.
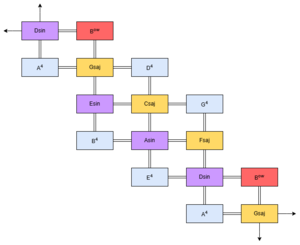
Example: Chord Progression in C Ionian (Superpyth)
The C Ionian scale in Superpyth is a perfect showcase of how common-practice harmony differs from that of 22edo; specifically, quartal harmony tends to provide a more resolved sound than tertian harmony does, due to the sharp fifth exaggerating the size of the chroma. Thus, our progression can resolve quite nicely to the tonic chord, Csus4 or G4/C.
A supermajor triad can be found over the fifth degree of the Ionian mode, which is much tenser than the major triad found in Meantone tunings due to the major seventh (the third of the V chord) being significantly sharper; this increases the strength of the pull towards the tonic, as well as destabilizes the V chord, making it clear that this is not a place of rest and thus negating the need for a dominant seventh over that chord. This allows us to restrict our progression to three-part harmony rather than switching between three- and four-part harmony as is often done in common-practice progressions.
Note also that a leading tone occurs between the notes E and F; this allows us to achieve a false resolution onto the Fsus4 chord, or C4/F, in our progression by way of voice leading from a chord on E. For this example, I have chosen to use the Orwell Diminished triad over E, which provides a tense sound without sounding nasty. The Fsus4 and Eow chords also introduce B♭, which contrasts with the B♮ found in the Gsaj chord, displaying how notes pulled from outside of the original scale can be quite useful in writing harmonies.
Thus, our four-chord progression is Csus4 - eow - Fsus4 - Gsaj. This series of chords uses a combination of voice leading, tension-and-release paradigms, and circle of fifths movement to provide a dynamic and functional harmonic progression.