46edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older edit
VisualWikitext
ArrowHead294 (talk | contribs)
14,512 edits
Sintel (talk | contribs)
autopatrolled, emailconfirmed
1,547 edits
→Approximation to JI: -zeta peak index
 
(38 intermediate revisions by 13 users not shown)
Line 6: Line 6:
}}
}}
{{Infobox ET}}
{{Infobox ET}}
{{EDO intro|46}}
{{ED intro}}


== Theory ==
== Theory ==
In the opinion of some, 46edo is the first equal division to deal adequately with the [[13-limit]], though others award that distinction to [[41edo]] or [[53edo]]. In fact, while 41 is a [[The Riemann zeta function and tuning #Zeta EDO lists|zeta peak and zeta integral edo]] but not a [[The Riemann zeta function and tuning #Zeta EDO lists|zeta gap edo]], 46 is zeta gap but not zeta peak or zeta integral, and 53 is a [[strict zeta edo]]. Like 41 and 53, 46 is distinctly [[consistent]] in the [[9-odd-limit]], and it is consistent to the [[13-odd-limit]] or the no-15 no-19 [[23-odd-limit]]. 46edo's fifth is slightly sharp of just, which some people (e.g. [[Margo Schulter]]) prefer, sometimes strongly, over both the [[3/2|just fifth]] and fifths of temperaments with flat fifths, such as meantone. Many say that sharp fifths give a characteristic bright sound to 5-limit triads, and consider the sound of meantone triads to be more mellow in comparison.
In the opinion of some, 46edo is the first equal division to deal adequately with the [[13-limit]], though others award that distinction to [[41edo]] or [[53edo]]. 46edo's fifth is slightly sharp of just, which some people (e.g. [[Margo Schulter]]) prefer, sometimes strongly, over both the [[3/2|just fifth]] and fifths of temperaments with flat fifths, such as meantone. Many say that sharp fifths give a characteristic bright sound to 5-limit triads, and consider the sound of meantone triads to be more mellow in comparison. 46edo is not a [[The Riemann zeta function and tuning #Zeta EDO lists|zeta peak edo]], but it is a [[The Riemann zeta function and tuning #Zeta EDO lists|zeta gap edo]]. It is distinctly [[consistent]] in the [[9-odd-limit]], and it is consistent to the [[13-odd-limit]] or the no-15 no-19 [[23-odd-limit]].


[[Rank-2 temperament]]s it [[support]]s include [[sensi]], [[valentine]], [[shrutar]], [[rodan]], [[leapday]], [[parapyth]], and [[unidec]]. The [[11-odd-limit]] [[minimax tuning]] for valentine, (11/7)<sup>1/10</sup>, is only 0.01 cents flat of 3\46 octaves.  
46edo is also notable for being the smallest equal division to approximate harmonics 3, 5, 7, 11, and 13 with less than 25% [[relative interval error]].
 
[[Rank-2 temperament]]s it [[support]]s include [[sensi]], [[valentine]], [[shrutar]], [[rodan]], [[leapday]], and [[unidec]]. The [[11-odd-limit]] [[minimax tuning]] for valentine, (11/7)<sup>1/10</sup>, is only 0.01 cents flat of 3\46 octaves.  


[[Magic22 as srutis #Shrutar.5B22.5D_as_srutis|Shrutar22 as srutis]] describes a possible use of 46edo for [[Indian]] music.
[[Magic22 as srutis #Shrutar.5B22.5D_as_srutis|Shrutar22 as srutis]] describes a possible use of 46edo for [[Indian]] music.


=== Prime harmonics ===
=== Prime harmonics ===
{{Harmonics in equal|46|columns=12}}
{{Harmonics in equal|46|columns=9}}
{{Harmonics in equal|46|columns=12|start=13|collapsed=true|title=Approximation of prime harmonics in 46edo (continued)}}
{{Harmonics in equal|46|columns=9|start=10|collapsed=true|title=Approximation of prime harmonics in 46edo (continued)}}


=== Subsets and supersets ===
=== Subsets and supersets ===
Line 27: Line 29:
! &#35;
! &#35;
! Cents
! Cents
! Approximate Ratios<ref name="interval ratios" group="note">Based on treating 46edo as a 2.3.5.7.11.13.17.23 subgroup, without ratios of 15 (except the superparticulars). 46edo has intervals involving the 15th harmonic poorly approximated, except for 15/8 and 16/15 themselves, because, while the 3rd and 5th harmonics are sharp and their deviations from just intonation add up, 7, 11, and 13 are all tuned flat, making the difference even larger. This prevents it from being [[consistent]] in the [[15-odd-limit]], as there is a discrepancy approximating [[15/13]] and [[26/15]]&mdash;9\46 is closer to 15/13 by a hair, but 10\46 represents the difference between 46edo's 15/8 and 13/8 and is more likely to appear in chords actually functioning as 15/13.</ref>
! Approximate ratios<ref name="interval ratios" group="note">{{sg|limit=2.3.5.7.11.13.17.23&nbsp;subgroup}} However, ratios of 15 are not included here, as except for 15/8 and 16/15 themselves 46edo has intervals involving the 15th harmonic poorly approximated in general. This is because, while the 3rd and 5th harmonics are sharp and their deviations from just intonation add up, 7, 11, and 13 are all tuned flat, making the difference even larger. This prevents it from being [[consistent]] in the [[15-odd-limit]], as there is a discrepancy approximating [[15/13]] and [[26/15]]&mdash;9\46 is closer to 15/13 by a hair, but 10\46 represents the difference between 46edo's 15/8 and 13/8 and is more likely to appear in chords actually functioning as 15/13.</ref>
! colspan="3" | [[Ups and Downs Notation]]
! colspan="3" | [[Ups and downs notation]]
! colspan="3" | [[SKULO interval names| SKULO notation]] (K or S = 1, U = 2)
([[Enharmonic unisons in ups and downs notation|EUs]]: v<sup>5</sup>A1 and ^^d2)
! colspan="2" | [[Solfege| Solfeges]]
! colspan="3" | [[SKULO interval names|SKULO notation]] (K or S = 1, U = 2)
! colspan="2" | [[Solfege]]
|-
|-
| 0
| 0
| 0.000
| 0.0
| [[1/1]]
| [[1/1]]
| perfect unison
| perfect unison
Line 45: Line 48:
|-
|-
| 1
| 1
| 26.087
| 26.1
| [[81/80]], [[64/63]], [[49/48]]
| [[81/80]], [[64/63]], [[49/48]]
| up unison
| up unison
| ^1
| ^1
| ^D
| ^D
| comma-wide unison,  
| comma-wide unison, <br>super unison
super unison
| K1, S1
| K1, S1
| KD, SD
| KD, SD
Line 58: Line 60:
|-
|-
| 2
| 2
| 52.174
| 52.2
| [[28/27]], [[36/35]], [[33/32]]
| [[28/27]], [[36/35]], [[33/32]]
| downminor 2nd
| downminor 2nd
Line 70: Line 72:
|-
|-
| 3
| 3
| 78.261
| 78.3
| [[25/24]], [[21/20]], [[22/21]], [[24/23]], [[23/22]]
| [[25/24]], [[21/20]], [[22/21]], [[24/23]], [[23/22]]
| minor 2nd
| minor 2nd
| m2
| m2
| Eb
| Eb
| minor 2nd,  
| minor 2nd, <br>classic augmented unison
classic augmented unison
| m2, kkA1
| m2, kkA1
| Eb, kkD#
| Eb, kkD#
Line 83: Line 84:
|-
|-
| 4
| 4
| 104.348
| 104.3
| [[16/15]], [[17/16]], [[18/17]]
| [[16/15]], [[17/16]], [[18/17]]
| upminor 2nd
| upminor 2nd
| ^m2
| ^m2
| ^Eb
| ^Eb
| classic minor 2nd,  
| classic minor 2nd, <br>comma-narrow aug unison
comma-narrow aug unison
| Km2, kA1
| Km2, kA1
| KEb, kD#
| KEb, kD#
Line 96: Line 96:
|-
|-
| 5
| 5
| 130.435
| 130.4
| [[13/12]], [[14/13]], [[15/14]]
| [[13/12]], [[14/13]], [[15/14]]
| dupminor 2nd
| dupminor 2nd
Line 108: Line 108:
|-
|-
| 6
| 6
| 156.522
| 156.5
| [[12/11]], [[11/10]], [[23/21]]
| [[12/11]], [[11/10]], [[23/21]]
| dudmajor 2nd
| dudmajor 2nd
| vvM2
| vvM2
| vvE
| vvE
| greater neutral second,  
| greater neutral second, <br>super aug unison
super aug unison
| N2, sA1
| N2, sA1
| uE, sD#
| uE, sD#
Line 121: Line 120:
|-
|-
| 7
| 7
| 182.609
| 182.6
| [[10/9]]
| [[10/9]]
| downmajor 2nd
| downmajor 2nd
Line 133: Line 132:
|-
|-
| 8
| 8
| 208.696
| 208.7
| [[9/8]]
| [[9/8]]
| major 2nd
| major 2nd
Line 145: Line 144:
|-
|-
| 9
| 9
| 234.783
| 234.8
| [[8/7]], [[23/20]]
| [[8/7]], [[23/20]]
| upmajor 2nd
| upmajor 2nd
Line 157: Line 156:
|-
|-
| 10
| 10
| 260.870
| 260.9
| [[7/6]]
| [[7/6]]
| downminor 3rd
| downminor 3rd
Line 169: Line 168:
|-
|-
| 11
| 11
| 286.957
| 287.0
| [[13/11]], [[20/17]]
| [[13/11]], [[20/17]]
| minor 3rd
| minor 3rd
Line 181: Line 180:
|-
|-
| 12
| 12
| 313.043
| 313.0
| [[6/5]]
| [[6/5]]
| upminor 3rd
| upminor 3rd
Line 193: Line 192:
|-
|-
| 13
| 13
| 339.130
| 339.1
| [[11/9]], [[17/14]], [[28/23]]
| [[11/9]], [[17/14]], [[28/23]]
| dupminor 3rd
| dupminor 3rd
Line 205: Line 204:
|-
|-
| 14
| 14
| 365.217
| 365.2
| [[16/13]], [[26/21]], [[21/17]]
| [[16/13]], [[26/21]], [[21/17]]
| dudmajor 3rd
| dudmajor 3rd
Line 217: Line 216:
|-
|-
| 15
| 15
| 391.304
| 391.3
| [[5/4]]
| [[5/4]]
| downmajor 3rd
| downmajor 3rd
Line 229: Line 228:
|-
|-
| 16
| 16
| 417.391
| 417.4
| [[14/11]], [[23/18]]
| [[14/11]], [[23/18]]
| major 3rd
| major 3rd
Line 241: Line 240:
|-
|-
| 17
| 17
| 443.478
| 443.5
| [[9/7]], [[13/10]], [[22/17]]
| [[9/7]], [[13/10]], [[22/17]]
| upmajor 3rd
| upmajor 3rd
Line 253: Line 252:
|-
|-
| 18
| 18
| 469.565
| 469.6
| [[21/16]], [[17/13]]
| [[21/16]], [[17/13]]
| down 4th
| down 4th
Line 265: Line 264:
|-
|-
| 19
| 19
| 495.652
| 495.7
| [[4/3]]
| [[4/3]]
| perfect 4th
| perfect 4th
Line 277: Line 276:
|-
|-
| 20
| 20
| 521.739
| 521.7
| [[27/20]], [[23/17]]
| [[27/20]], [[23/17]]
| up 4th
| up 4th
Line 289: Line 288:
|-
|-
| 21
| 21
| 547.826
| 547.8
| [[11/8]]
| [[11/8]]
| dup 4th
| dup 4th
Line 301: Line 300:
|-
|-
| 22
| 22
| 573.913
| 573.9
| [[7/5]], [[18/13]], [[32/23]]
| [[7/5]], [[18/13]], [[32/23]]
| dudaug 4th,  
| dudaug 4th, <br>dim 5th
dim 5th
| vvA4, d5
| vvA4, d5
| vvG#, Ab
| vvG#, Ab
Line 314: Line 312:
|-
|-
| 23
| 23
| 600.000
| 600.0
| [[17/12]], [[24/17]]
| [[17/12]], [[24/17]]
| downaug 4th, updim 5th
| downaug 4th, updim 5th
| vA4, ^d5
| vA4, ^d5
| vG#, ^Ab
| vG#, ^Ab
| comma-narrow aug 4th,  
| comma-narrow aug 4th, <br>comma-wide dim 5th
comma-wide dim 5th
| kA4, Kd5
| kA4, Kd5
| kG#, KAb
| kG#, KAb
Line 327: Line 324:
|-
|-
| 24
| 24
| 626.087
| 626.1
| [[10/7]], [[13/9]], [[23/16]]
| [[10/7]], [[13/9]], [[23/16]]
| aug 4th, dupdim 5th
| aug 4th, dupdim 5th
| A4, ^^d5
| A4, ^^d5
| G#, ^^Ab
| G#, ^^Ab
| augmented 4th,  
| augmented 4th, <br>classic diminished 5th
classic diminished 5th
| A4, KKd5
| A4, KKd5
| G#, KKAb
| G#, KKAb
Line 340: Line 336:
|-
|-
| 25
| 25
| 652.174
| 652.2
| [[16/11]]
| [[16/11]]
| dud 5th
| dud 5th
| vv5
| vv5
| vvA
| vvA
| super augmented 4th,  
| super augmented 4th, <br>unter 5th
unter 5th
| SA4, u5
| SA4, u5
| SG#, uA
| SG#, uA
Line 353: Line 348:
|-
|-
| 26
| 26
| 678.261
| 678.3
| [[40/27]], [[34/23]]
| [[40/27]], [[34/23]]
| down 5th
| down 5th
Line 365: Line 360:
|-
|-
| 27
| 27
| 704.348
| 704.3
| [[3/2]]
| [[3/2]]
| perfect 5th
| perfect 5th
Line 377: Line 372:
|-
|-
| 28
| 28
| 730.435
| 730.4
| [[32/21]], [[26/17]]
| [[32/21]], [[26/17]]
| up 5th
| up 5th
Line 389: Line 384:
|-
|-
| 29
| 29
| 756.522
| 756.5
| [[14/9]], [[20/13]], [[17/11]]
| [[14/9]], [[20/13]], [[17/11]]
| downminor 6th
| downminor 6th
Line 401: Line 396:
|-
|-
| 30
| 30
| 782.609
| 782.6
| [[11/7]]
| [[11/7]]
| minor 6th
| minor 6th
Line 413: Line 408:
|-
|-
| 31
| 31
| 808.696
| 808.7
| [[8/5]]
| [[8/5]]
| upminor 6th
| upminor 6th
Line 425: Line 420:
|-
|-
| 32
| 32
| 834.783
| 834.8
| [[13/8]], [[21/13]], [[34/21]]
| [[13/8]], [[21/13]], [[34/21]]
| dupminor 6th
| dupminor 6th
Line 437: Line 432:
|-
|-
| 33
| 33
| 860.870
| 860.9
| [[18/11]], [[28/17]], [[23/14]]
| [[18/11]], [[28/17]], [[23/14]]
| dudmajor 6th
| dudmajor 6th
Line 449: Line 444:
|-
|-
| 34
| 34
| 886.957
| 887.0
| [[5/3]]
| [[5/3]]
| downmajor 6th
| downmajor 6th
Line 461: Line 456:
|-
|-
| 35
| 35
| 913.043
| 913.0
| [[22/13]], [[17/10]]
| [[22/13]], [[17/10]]
| major 6th
| major 6th
Line 473: Line 468:
|-
|-
| 36
| 36
| 939.130
| 939.1
| [[12/7]]
| [[12/7]]
| upmajor 6th
| upmajor 6th
Line 485: Line 480:
|-
|-
| 37
| 37
| 965.217
| 965.2
| [[7/4]], [[40/23]]
| [[7/4]], [[40/23]]
| downminor 7th
| downminor 7th
Line 497: Line 492:
|-
|-
| 38
| 38
| 991.304
| 991.3
| [[16/9]], [[23/13]]
| [[16/9]], [[23/13]]
| minor 7th
| minor 7th
Line 509: Line 504:
|-
|-
| 39
| 39
| 1017.391
| 1017.4
| [[9/5]]
| [[9/5]]
| upminor 7th
| upminor 7th
Line 521: Line 516:
|-
|-
| 40
| 40
| 1043.478
| 1043.5
| [[11/6]], [[20/11]], [[42/23]]
| [[11/6]], [[20/11]], [[42/23]]
| dupminor 7th
| dupminor 7th
Line 533: Line 528:
|-
|-
| 41
| 41
| 1069.565
| 1069.6
| [[24/13]], [[13/7]], [[28/15]]
| [[24/13]], [[13/7]], [[28/15]]
| dudmajor 7th
| dudmajor 7th
Line 546: Line 541:
|-
|-
| 42
| 42
| 1095.652
| 1095.7
| [[15/8]], [[32/17]], [[17/9]]
| [[15/8]], [[32/17]], [[17/9]]
| downmajor 7th
| downmajor 7th
Line 559: Line 554:
|-
|-
| 43
| 43
| 1121.739
| 1121.7
| [[48/25]], [[40/21]], [[21/11]], [[23/12]], [[44/23]]
| [[48/25]], [[40/21]], [[21/11]], [[23/12]], [[44/23]]
| major 7th
| major 7th
| M7
| M7
| C#
| C#
| major 7th,  
| major 7th, <br>classic diminished 8ve
classic diminished 8ve
| M7, KKd8
| M7, KKd8
| C#, KKDb
| C#, KKDb
Line 572: Line 566:
|-
|-
| 44
| 44
| 1147.826
| 1147.8
| [[27/14]], [[35/18]], [[64/33]]
| [[27/14]], [[35/18]], [[64/33]]
| upmajor 7th
| upmajor 7th
Line 584: Line 578:
|-
|-
| 45
| 45
| 1173.913
| 1173.9
| [[160/81]], [[63/32]], [[96/49]]
| [[160/81]], [[63/32]], [[96/49]]
| down 8ve
| down 8ve
Line 596: Line 590:
|-
|-
| 46
| 46
| 1200.000
| 1200.0
| [[2/1]]
| [[2/1]]
| perfect 8ve
| perfect 8ve
Line 620: Line 614:
| downminor
| downminor
| zo
| zo
| {a, b, 0, 1}
| [a, b, 0, 1>
| 7/6, 7/4
| 7/6, 7/4
|-
|-
| minor
| minor
| fourthward wa
| fourthward wa
| {a, b}, b &lt; -1
| [a, b>, b &lt; −1
| 32/27, 16/9
| 32/27, 16/9
|-
|-
| upminor
| upminor
| gu
| gu
| {a, b, -1}
| [a, b, −1>
| 6/5, 9/5
| 6/5, 9/5
|-
|-
| dupminor
| dupminor
| ilo
| ilo
| {a, b, 0, 0, 1}
| [a, b, 0, 0, 1>
| 11/9, 11/6
| 11/9, 11/6
|-
|-
| dudmajor
| dudmajor
| lu
| lu
| {a, b, 0, 0, -1}
| [a, b, 0, 0, −1>
| 12/11, 18/11
| 12/11, 18/11
|-
|-
| downmajor
| downmajor
| yo
| yo
| {a, b, 1}
| [a, b, 1>
| 5/4, 5/3
| 5/4, 5/3
|-
|-
| major
| major
| fifthward wa
| fifthward wa
| {a, b}, b &gt; 1
| [a, b>, b &gt; 1
| 9/8, 27/16
| 9/8, 27/16
|-
|-
| upmajor
| upmajor
| ru
| ru
| {a, b, 0, -1}
| [a, b, 0, −1>
| 9/7, 12/7
| 9/7, 12/7
|}
|}
Line 671: Line 665:
| zo
| zo
| 6:7:9
| 6:7:9
| 0-10-27
| 0–10–27
| C vEb G
| C vEb G
| Cvm
| Cvm
Line 678: Line 672:
| gu
| gu
| 10:12:15
| 10:12:15
| 0-12-27
| 0–12–27
| C ^Eb G
| C ^Eb G
| C^m
| C^m
Line 685: Line 679:
| ilo
| ilo
| 18:22:27
| 18:22:27
| 0-13-27
| 0–13–27
| C ^^Eb G
| C ^^Eb G
| C^^m
| C^^m
Line 692: Line 686:
| lu
| lu
| 22:27:33
| 22:27:33
| 0-14-27
| 0–14–27
| C vvE G
| C vvE G
| Cvv
| Cvv
Line 699: Line 693:
| yo
| yo
| 4:5:6
| 4:5:6
| 0-15-27
| 0–15–27
| C vE G
| C vE G
| Cv
| Cv
Line 706: Line 700:
| ru
| ru
| 14:18:21
| 14:18:21
| 0-17-27
| 0–17–27
| C ^E G
| C ^E G
| C^
| C^
| C upmajor or C up
| C upmajor or C up
|}
|}
For a more complete list, see [[Ups and Downs Notation #Chords and Chord Progressions]].
For a more complete list, see [[Ups and downs notation #Chords and chord progressions]].


== Notation ==
== Notation ==
=== Sagittal ===
=== Ups and downs notation ===
The following table shows [[sagittal notation]] accidentals in one apotome for 46edo.  
46edo can be notated with [[ups and downs]], spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).
{{Sharpness-sharp5a}}
Another notation uses [[Alternative symbols for ups and downs notation#Sharp-5|alternative ups and downs]]. Here, this can be done using sharps and flats with arrows, borrowed from extended [[Helmholtz–Ellis notation]]:
{{Sharpness-sharp5}}
 
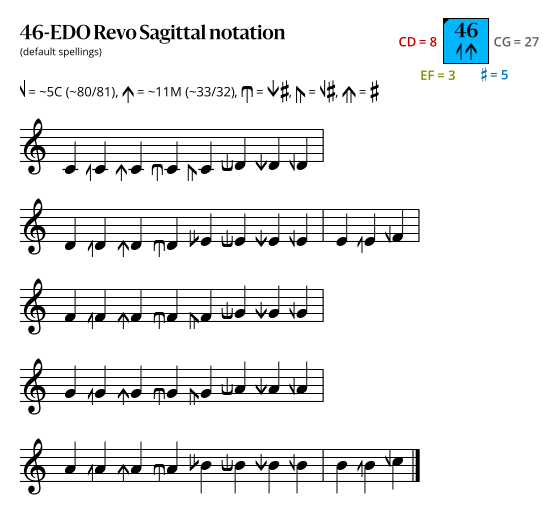
=== Sagittal notation ===
This notation uses the same sagittal sequence as [[39edo #Sagittal notation|39edo]].


{| class="wikitable center-all"
==== Evo flavor ====
! Steps
<imagemap>
| 0
File:46-EDO_Evo_Sagittal.svg
| 1
desc none
| 2
rect 80 0 300 50 [[Sagittal_notation]]
| 3
rect 300 0 511 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
| 4
rect 20 80 120 106 [[81/80]]
| 5
rect 120 80 240 106 [[33/32]]
|-
default [[File:46-EDO_Evo_Sagittal.svg]]
! Symbol
</imagemap>
| [[File:Sagittal natural.png]]
| [[File:Sagittal pai.png]]
| [[File:Sagittal pakai.png]]
| [[File:Sagittal jatai.png]]
| [[File:Sagittal sharp pao.png]]
| [[File:Sagittal sharp.png]]
|}


=== Ups and downs notation ===
==== Revo flavor ====
Using [[Helmholtz-Ellis notation|Helmholtz&ndash;Ellis]] accidentals, 46edo can also be notated using [[ups and downs notation]]:
<imagemap>
{{Sharpness-sharp5}}
File:46-EDO_Revo_Sagittal.svg
Here, a sharp raises by five steps, and a flat lowers by five steps, so single and double arrows can be used to fill in the gap. If the arrows are taken to have their own layer of enharmonic spellings, some notes may be best spelled with three arrows.
desc none
rect 80 0 300 50 [[Sagittal_notation]]
rect 300 0 557 80 [https://sagittal.org#periodic-table Periodic table of EDOs with sagittal notation]
rect 20 80 120 106 [[81/80]]
rect 120 80 240 106 [[33/32]]
default [[File:46-EDO_Revo_Sagittal.svg]]
</imagemap>


== Approximation to JI ==
== Approximation to JI ==
Line 757: Line 756:
| [[10/9]] || 36.1% || Normal || [[Mitonic]] || [[Unidec]], [[hendec]]
| [[10/9]] || 36.1% || Normal || [[Mitonic]] || [[Unidec]], [[hendec]]
|-
|-
| [[31/24]] || 70.2% || Weak || ? || ?
| [[31/24]] || 70.2% || Weak || [[Sensible]], [[sensi]] add-31 || [[Bison]] add-31, [[bisensi]] add-31
|}
|}


Line 778: Line 777:
|}
|}


''For the 23rd-octave temperament that 46edo supports which combines all above 23-note circles, see:'' [[Icositritonic]].
For the 23rd-octave temperament that 46edo supports which combines all above 23-note circles, see [[icositritonic]].


== Regular temperament properties ==
== Regular temperament properties ==
{| class="wikitable center-4 center-5 center-6"
{| class="wikitable center-4 center-5 center-6"
|-
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Subgroup]]
! rowspan="2" | [[Comma list]]
! rowspan="2" | [[Comma list]]
Line 843: Line 843:


=== Commas ===
=== Commas ===
This is a partial list of the [[commas]] that 46edo [[tempers out]] with its patent [[val]], {{val| 24 38 56 67 83 89 }}.  
This is a partial list of the [[commas]] that 46et [[tempering out|tempers out]] with its [[patent val]], {{val| 24 38 56 67 83 89 }}.  


{| class="commatable wikitable center-1 center-2 right-4 center-5"
{| class="commatable wikitable center-1 center-2 right-4 center-5"
Line 1,000: Line 1,000:
| Thothotrigu
| Thothotrigu
|  
|  
|-
| 13
| [[351/350]]
| {{Monzo| -1 3 -2 -1 0 1 }}
| 4.94
| Thorugugu
| Ratwolfsma
|-
| 13
| [[352/351]]
| {{monzo| 5 -3 0 0 1 -1 }}
| 4.93
| Thulo
| Minor minthma
|-
|-
| 17
| 17
Line 1,019: Line 1,033:
{| class="wikitable center-1 center-2 center-3 center-4"
{| class="wikitable center-1 center-2 center-3 center-4"
|-
|-
! Periods <br />per 8ve
! Periods<br>per 8ve
! Generator
! Generator
! Cents
! Cents
! Temperaments
! Temperaments
! MOS Scales
! MOS scales
! L:s
! L:s
|-
|-
Line 1,036: Line 1,050:
| 78.261
| 78.261
| [[Valentine]]
| [[Valentine]]
| 1L 14s (15-tone)<br>15L 1s (16-tone)<br>16L 15s (31-tone)
| 1L&nbsp;14s (15-tone)<br>15L&nbsp;1s (16-tone)<br>16L&nbsp;15s (31-tone)
| 4:3 ~ [[Maximal evenness|quasi-equal]]<br>3:1<br>2:1 ~ QE
| 4:3 ~ [[Maximal evenness|quasi-equal]]<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,042: Line 1,056:
| 130.435
| 130.435
| [[Twothirdtonic]]
| [[Twothirdtonic]]
| [[1L 8s]] (9-tone)<br>[[9L 1s]] (10-tone)<br>9L 10s (19-tone)<br>9L 19s (28-tone)<br>9L 28s (37-tone)
| [[1L&nbsp;8s]] (9-tone)<br>[[9L&nbsp;1s]] (10-tone)<br>9L&nbsp;10s (19-tone)<br>9L&nbsp;19s (28-tone)<br>9L&nbsp;28s (37-tone)
| 6:5 ~ QE<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
| 6:5 ~ QE<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,048: Line 1,062:
| 182.609
| 182.609
| [[Minortone]] / [[mitonic]]
| [[Minortone]] / [[mitonic]]
| [[1L 5s]] (6-tone)<br>[[6L 1s]] (7-tone)<br>7L 6s (13-tone)<br>13L 7s (20-tone)<br>13L 20s (33-tone)
| [[1L&nbsp;5s]] (6-tone)<br>[[6L&nbsp;1s]] (7-tone)<br>7L&nbsp;6s (13-tone)<br>13L&nbsp;7s (20-tone)<br>13L&nbsp;20s (33-tone)
| 11:7<br>7:4<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
| 11:7<br>7:4<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,054: Line 1,068:
| 234.783
| 234.783
| [[Rodan]]
| [[Rodan]]
| [[1L 4s]] (5-tone)<br>[[1L 5s]] (6-tone)<br>[[5L 6s]] (11-tone)<br>5L 11s (16-tone)<br>5L 16s (21-tone)<br>5L 21s (26-tone)<br>5L 26s (31-tone)<br>5L 31s (36-tone)<br>5L 36s (41-tone)
| [[1L&nbsp;4s]] (5-tone)<br>[[1L&nbsp;5s]] (6-tone)<br>[[5L&nbsp;6s]] (11-tone)<br>5L&nbsp;11s (16-tone)<br>5L&nbsp;16s (21-tone)<br>5L&nbsp;21s (26-tone)<br>5L&nbsp;26s (31-tone)<br>5L&nbsp;31s (36-tone)<br>5L&nbsp;36s (41-tone)
| 10:9 ~QE<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE, Pathological
| 10:9 ~QE<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 11\46
| 11\46
| 286.957
| 286.957
| [[Amity_family#Gamity|Gamity]]
| [[Amity_family#Gamity|Gamity]]
| [[4L 1s]] (5-tone)<br>[[4L 5s]] (9-tone)<br>4L 9s (13-tone)<br>4L 13s (17-tone)<br>4L 17s (21-tone)<br>21L 4s (25-tone)
| [[4L&nbsp;1s]] (5-tone)<br>[[4L&nbsp;5s]] (9-tone)<br>4L&nbsp;9s (13-tone)<br>4L&nbsp;13s (17-tone)<br>4L&nbsp;17s (21-tone)<br>21L&nbsp;4s (25-tone)
| 11:2<br>9:2<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 11:2<br>9:2<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,066: Line 1,080:
| 339.130
| 339.130
| [[Amity]] / [[hitchcock]]
| [[Amity]] / [[hitchcock]]
| [[4L 3s]] (7-tone)<br>[[7L 4s]] (11-tone)<br>7L 11s (18-tone)<br>7L 18s (25-tone)<br>7L 25s (32-tone)<br>7L 32s (39-tone)
| [[4L&nbsp;3s]] (7-tone)<br>[[7L&nbsp;4s]] (11-tone)<br>7L&nbsp;11s (18-tone)<br>7L&nbsp;18s (25-tone)<br>7L&nbsp;25s (32-tone)<br>7L&nbsp;32s (39-tone)
| 7:6 ~ QE<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE! Pathological
| 7:6 ~ QE<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 15\46
| 15\46
| 391.304
| 391.304
| [[Magus]] / [[amigo]]
| [[Magus]] / [[amigo]]
| [[1L 2s]] (3-tone)<br>[[3L 1s]] (4-tone)<br>[[3L 4s]] (7-tone)<br>[[3L 7s]] (10-tone)<br>3L 10s (13-tone)<br>3L 13s (16-tone)<br>3L 16s (19-tone)<br>3L 19s (21-tone)<br>3L 21s (24-tone)<br>3L 24s (27-tone)<br>3L 27s (30-tone)<br>3L 30s (33-tone)<br>3L 33s (36-tone)<br>3L 36s (39-tone)<br>3L 39s (42-tone)
| [[1L&nbsp;2s]] (3-tone)<br>[[3L&nbsp;1s]] (4-tone)<br>[[3L&nbsp;4s]] (7-tone)<br>[[3L&nbsp;7s]] (10-tone)<br>3L&nbsp;10s (13-tone)<br>3L&nbsp;13s (16-tone)<br>3L&nbsp;16s (19-tone)<br>3L&nbsp;19s (21-tone)<br>3L&nbsp;21s (24-tone)<br>3L&nbsp;24s (27-tone)<br>3L&nbsp;27s (30-tone)<br>3L&nbsp;30s (33-tone)<br>3L&nbsp;33s (36-tone)<br>3L&nbsp;36s (39-tone)<br>3L&nbsp;39s (42-tone)
| 16:15 ~ QE<br>15:1<br>14:1<br>13:1<br>12:1<br>11:1<br>10:1<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1 ~ Pathological<br>2:1 ~ QE, Pathological
| 16:15 ~ QE<br>15:1<br>14:1<br>13:1<br>12:1<br>11:1<br>10:1<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 17\46
| 17\46
| 443.478
| 443.478
| [[Sensi]]
| [[Sensi]]
| [[3L 2s]] (5-tone)<br>[[3L 5s]] (8-tone)<br>[[8L 3s]] (11-tone)<br>8L 11s (19-tone)<br>19L 8s (27-tone)
| [[3L&nbsp;2s]] (5-tone)<br>[[3L&nbsp;5s]] (8-tone)<br>[[8L&nbsp;3s]] (11-tone)<br>8L&nbsp;11s (19-tone)<br>19L&nbsp;8s (27-tone)
| 12:5<br>7:5<br>5:2<br>3:2 ~ QE, Golden<br>2:1
| 12:5<br>7:5<br>5:2<br>3:2 ~ QE, Golden<br>2:1
|-
|-
Line 1,084: Line 1,098:
| 495.652
| 495.652
| [[Leapday]]
| [[Leapday]]
| [[2L 3s]] (5-tone)<br>[[5L 2s]] (7-tone)<br>[[5L 7s]] (12-tone)<br>12L 5s (17-tone)<br>17L 12s (29-tone)
| [[2L&nbsp;3s]] (5-tone)<br>[[5L&nbsp;2s]] (7-tone)<br>[[5L&nbsp;7s]] (12-tone)<br>12L&nbsp;5s (17-tone)<br>17L&nbsp;12s (29-tone)
| 11:8<br>8:3<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 11:8<br>8:3<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,090: Line 1,104:
| 547.826
| 547.826
| [[Heinz]]
| [[Heinz]]
| [[2L 3s]] (5-tone)<br>[[2L 5s]] (7-tone)<br>[[2L 7s]] (9-tone)<br>[[2L 9s]] (11-tone)<br>11L 2s (13-tone)<br>11L 13s (24-tone)<br>11L 24s (35-tone)
| [[2L&nbsp;3s]] (5-tone)<br>[[2L&nbsp;5s]] (7-tone)<br>[[2L&nbsp;7s]] (9-tone)<br>[[2L&nbsp;9s]] (11-tone)<br>11L&nbsp;2s (13-tone)<br>11L&nbsp;13s (24-tone)<br>11L&nbsp;24s (35-tone)
| 17:4<br>13:4<br>9:4<br>5:4 ~ QE<br>4:1<br>3:1<br>2:1 ~ QE
| 17:4<br>13:4<br>9:4<br>5:4 ~ QE<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,103: Line 1,117:
| 52.174
| 52.174
| [[Shrutar]]
| [[Shrutar]]
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[2L 6s]] (8-tone)<br>[[2L 8s]] (10-tone)<br>[[2L 10s]] (12-tone)<br>2L 12s (14-tone)<br>2L 14s (16-tone)<br>2L 16s (18-tone)<br>2L 18s (20-tone)<br>2L 20s (22-tone)<br>22L 2s (24-tone)
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[2L&nbsp;6s]] (8-tone)<br>[[2L&nbsp;8s]] (10-tone)<br>[[2L&nbsp;10s]] (12-tone)<br>2L&nbsp;12s (14-tone)<br>2L&nbsp;14s (16-tone)<br>2L&nbsp;16s (18-tone)<br>2L&nbsp;18s (20-tone)<br>2L&nbsp;20s (22-tone)<br>22L&nbsp;2s (24-tone)
| 21:2<br>19:2<br>17:2<br>15:2<br>13:2<br>11:2<br>9:2<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 21:2<br>19:2<br>17:2<br>15:2<br>13:2<br>11:2<br>9:2<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,109: Line 1,123:
| 78.261
| 78.261
| [[Semivalentine]]
| [[Semivalentine]]
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[2L 6s]] (8-tone)<br>[[2L 8s]] (10-tone)<br>[[2L 10s]] (12-tone)<br>2L 12s (14-tone)<br>14L 2s (16-tone)<br>16L 14s (30-tone)
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[2L&nbsp;6s]] (8-tone)<br>[[2L&nbsp;8s]] (10-tone)<br>[[2L&nbsp;10s]] (12-tone)<br>2L&nbsp;12s (14-tone)<br>14L&nbsp;2s (16-tone)<br>16L&nbsp;14s (30-tone)
| 20:3<br>17:3<br>14:3<br>11:3<br>8:3<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 20:3<br>17:3<br>14:3<br>11:3<br>8:3<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,115: Line 1,129:
| 104.348
| 104.348
| [[Srutal]] / [[diaschismic]]
| [[Srutal]] / [[diaschismic]]
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[2L 6s]] (8-tone)<br>[[2L 8s]] (10-tone)<br>[[10L 2s]] (12-tone)<br>12L 10s (22-tone)<br>12L 22s (34-tone)
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[2L&nbsp;6s]] (8-tone)<br>[[2L&nbsp;8s]] (10-tone)<br>[[10L&nbsp;2s]] (12-tone)<br>12L&nbsp;10s (22-tone)<br>12L&nbsp;22s (34-tone)
| 19:4<br>15:4<br>11:4<br>7:4<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
| 19:4<br>15:4<br>11:4<br>7:4<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,121: Line 1,135:
| 130.435
| 130.435
|  
|  
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[2L 6s]] (8-tone)<br>[[8L 2s]] (10-tone)<br>8L 10s (18-tone)<br>18L 10s (28-tone)
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[2L&nbsp;6s]] (8-tone)<br>[[8L&nbsp;2s]] (10-tone)<br>8L&nbsp;10s (18-tone)<br>18L&nbsp;10s (28-tone)
| 18:5<br>13:5<br>8:5 ~ Golden<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 18:5<br>13:5<br>8:5 ~ Golden<br>5:3 ~ Golden<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,127: Line 1,141:
| 156.522
| 156.522
| [[Bison]]
| [[Bison]]
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[6L 2s]] (8-tone)<br>8L 6s (14-tone)<br>8L 14s (22-tone)<br>8L 22s (30-tone)<br>8L 30s (38-tone
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[6L&nbsp;2s]] (8-tone)<br>8L&nbsp;6s (14-tone)<br>8L&nbsp;14s (22-tone)<br>8L&nbsp;22s (30-tone)<br>8L&nbsp;30s (38-tone
| 17:6<br>11:6<br>6:5 ~ QE<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE, Pathological
| 17:6<br>11:6<br>6:5 ~ QE<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 7\46
| 7\46
| 182.609
| 182.609
| [[Unidec]] / [[hendec]]
| [[Unidec]] / [[hendec]]
| 2L 2s (4-tone)<br>[[2L 4s]] (6-tone)<br>[[6L 2s]] (8-tone)<br>6L 8s (14-tone)<br>6L 14s (20-tone)<br>20L 6s (26-tone)
| 2L&nbsp;2s (4-tone)<br>[[2L&nbsp;4s]] (6-tone)<br>[[6L&nbsp;2s]] (8-tone)<br>6L&nbsp;8s (14-tone)<br>6L&nbsp;14s (20-tone)<br>20L&nbsp;6s (26-tone)
| 16:7<br>9:7<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
| 16:7<br>9:7<br>7:2<br>5:2<br>3:2 ~ QE, Golden<br>2:1 ~ QE
|-
|-
Line 1,139: Line 1,153:
| 208.696
| 208.696
| [[Abigail]]
| [[Abigail]]
| 2L 2s (4-tone)<br>[[4L 2s]] (6-tone)<br>[[6L 2s]] (8-tone)<br>6L 8s (14-tone)<br>6L 14s (20-tone)<br>6L 20s (26-tone)<br>6L 26s (32-tone)<br>6L 32s (38-tone)<br>6L 38s (44-tone)
| 2L&nbsp;2s (4-tone)<br>[[4L&nbsp;2s]] (6-tone)<br>[[6L&nbsp;2s]] (8-tone)<br>6L&nbsp;8s (14-tone)<br>6L&nbsp;14s (20-tone)<br>6L&nbsp;20s (26-tone)<br>6L&nbsp;26s (32-tone)<br>6L&nbsp;32s (38-tone)<br>6L&nbsp;38s (44-tone)
| 15:8<br>8:7 ~ QE<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1 ~ Pathological<br>2:1 ~ QE, Pathological
| 15:8<br>8:7 ~ QE<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 9\46
| 9\46
| 234.783
| 234.783
| [[Echidnic]]
| [[Echidnic]]
| 2L 2s (4-tone)<br>[[4L 2s]] (6-tone)<br>[[6L 4s]] (10-tone)<br>10L 6s (16-tone)<br>10L 16s (26-tone)<br>10L 26s (36-tone)
| 2L&nbsp;2s (4-tone)<br>[[4L&nbsp;2s]] (6-tone)<br>[[6L&nbsp;4s]] (10-tone)<br>10L&nbsp;6s (16-tone)<br>10L&nbsp;16s (26-tone)<br>10L&nbsp;26s (36-tone)
| 14:9<br>9:5<br>5:4 ~ QE<br>4:1<br>3:1<br>2:1 ~ QE
| 14:9<br>9:5<br>5:4 ~ QE<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,151: Line 1,165:
| 260.87
| 260.87
| [[Bamity]]
| [[Bamity]]
| 2L 2s (4-tone)<br>[[4L 2s]] (6-tone)<br>[[4L 6s]] (10-tone)<br>4L 10s (14-tone)<br>14L 4s (18-tone)<br>14L 18s (32-tone)
| 2L&nbsp;2s (4-tone)<br>[[4L&nbsp;2s]] (6-tone)<br>[[4L&nbsp;6s]] (10-tone)<br>4L&nbsp;10s (14-tone)<br>14L&nbsp;4s (18-tone)<br>14L&nbsp;18s (32-tone)
| 13:10<br>10:3<br>7:3<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
| 13:10<br>10:3<br>7:3<br>4:3 ~ QE<br>3:1<br>2:1 ~ QE
|-
|-
Line 1,157: Line 1,171:
| 286.957
| 286.957
| [[Vines]]
| [[Vines]]
| 2L 2s (4-tone)<br>[[4L 2s]] (6-tone)<br>[[4L 6s]] (10-tone)<br>4L 10s (14-tone)<br>4L 14s (18-tone)<br>4L 18s (22-tone)<br>4L 22s (26-tone)<br>4L 26s (30-tone)<br>4L 30s (34-tone)<br>4L 34s (38-tone)<br>4L 38s (42-tone)
| 2L&nbsp;2s (4-tone)<br>[[4L&nbsp;2s]] (6-tone)<br>[[4L&nbsp;6s]] (10-tone)<br>4L&nbsp;10s (14-tone)<br>4L&nbsp;14s (18-tone)<br>4L&nbsp;18s (22-tone)<br>4L&nbsp;22s (26-tone)<br>4L&nbsp;26s (30-tone)<br>4L&nbsp;30s (34-tone)<br>4L&nbsp;34s (38-tone)<br>4L&nbsp;38s (42-tone)
| 12:11 ~ QE<br>11:1<br>10:1<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1 ~ Pathological<br>2:1 ~ QE, Pathological
| 12:11 ~ QE<br>11:1<br>10:1<br>9:1<br>8:1<br>7:1<br>6:1<br>5:1<br>4:1<br>3:1<br>2:1 ~ QE
|-
|-
| 23
| 23
Line 1,169: Line 1,183:


== Scales ==
== Scales ==
{{Main| List of MOS scales in 46edo }}
* [[Plum]]
* [[Plum]]
* [[Compdye]]
* [[Compdye]]
* [[Smi2s]]
* [[Smi2s]]


;Sensi
; Sensi
* [[Sensi5]]
* [[Sensi5]]
* [[Sensi8]]
* [[Sensi8]]
Line 1,179: Line 1,195:
* [[Sensi19]]
* [[Sensi19]]


;Elfleapday
; Elfleapday
* [[Elfleapday7]]
* [[Elfleapday7]]
* [[Elfleapday8d]]
* [[Elfleapday8d]]
Line 1,187: Line 1,203:
* [[Elfleapday12f]]
* [[Elfleapday12f]]


;Elfsensus
; Elfsensus
* [[Elfsensus7]]
* [[Elfsensus7]]
* [[Elfsensus8d]]
* [[Elfsensus8d]]
Line 1,194: Line 1,210:
* [[Elfsensus12]]
* [[Elfsensus12]]
* [[Elfsensus12f]]
* [[Elfsensus12f]]


=== Harmonic scales ===
=== Harmonic scales ===
46edo represents [[harmonic series|overtones]] 8 through 16 (written as [[JI]] ratios 8:9:10:11:12:13:14:15:16) with degrees 0, 8, 15, 21, 27, 32, 37, 42, 46. This corresponds to scale steps of 8, 7, 6, 6, 5, 5, 5, 4.
46edo represents [[harmonic series|overtones]] 8 through 16 (written as [[JI]] ratios 8:9:10:11:12:13:14:15:16) with degrees 0, 8, 15, 21, 27, 32, 37, 42, 46. This corresponds to scale steps of 8, 7, 6, 6, 5, 5, 5, 4.
* 8\46 (208.696&nbsp;&cent;) stands in for frequency ratio [[9/8]] (203.910¢).
* 8\46 (208.696{{c}}) stands in for frequency ratio [[9/8]] (203.910{{c}}).
* 7\46 (182.609&nbsp;&cent;) stands in for [[10/9]] (182.404¢).
* 7\46 (182.609{{c}}) stands in for [[10/9]] (182.404{{c}}).
* 6\46 (156.522&nbsp;&cent;) stands in for [[11/10]] (165.004¢) and [[12/11]] (150.637¢).
* 6\46 (156.522{{c}}) stands in for [[11/10]] (165.004{{c}}) and [[12/11]] (150.637{{c}}).
* 5\46 (130.435&nbsp;&cent;) stands in for [[13/12]] (138.573¢), [[14/13]] (128.298¢) and [[15/14]] (119.443¢).
* 5\46 (130.435{{c}}) stands in for [[13/12]] (138.573{{c}}), [[14/13]] (128.298{{c}}) and [[15/14]] (119.443{{c}}).
* 4\46 (104.348&nbsp;&cent;) stands in for [[16/15]] (111.731¢).
* 4\46 (104.348{{c}}) stands in for [[16/15]] (111.731{{c}}).
 
{| class="wikitable center-all"
{| class="wikitable center-all"
|-
|-
Line 1,218: Line 1,234:
|-
|-
! 7
! 7
| style="font-size: 16px;" | B{{flatdown|40}}
| style="font-size: 16px;" | G&#x1D12A;, B{{flatdown|40}}
|-
|-
! 9
! 9
Line 1,224: Line 1,240:
|-
|-
! 11
! 11
| style="font-size: 16px;" | F{{naturalup2|40}}
| style="font-size: 16px;" | E&#x266F;, F{{naturalup2|40}}
|-
|-
! 13
! 13
| style="font-size: 16px;" | A{{flatup2|40}}
| style="font-size: 16px;" | G&#x266F;, A{{flatup2|40}}
|-
|-
! 15
! 15
Line 1,234: Line 1,250:


== Instruments ==
== Instruments ==
* [[Skip fretting system 46 2 11]]: A skip-fretting system for playing 46-edo on a 23-edo stringed instrument.
=== Lumatone ===
* [[Lumatone mapping for 46edo]]
* [[Lumatone mapping for 46edo]]
=== Skip fretting ===
'''[[Skip fretting system 46 2 11]]''' is a [[skip fretting]] system for playing 46-edo on a 23-edo stringed instrument.
'''Skip fretting system 46 7 11''' is another skip fretting system for 46edo. The examples on this page are for 7-string [[guitar]].
; Harmonics
1/1: string 2 open
2/1: string 3 fret 5
3/2: not easily accessible
5/4: string 5 fret 4


== Music ==
== Music ==
=== Modern renditions ===
=== Modern renditions ===
; {{W|Johann Sebastian Bach}}
; {{W|Johann Sebastian Bach}}
* [https://www.youtube.com/watch?v=wMEdFl2puL0 "Ricercar a 6" from ''The Musical Offering'', BWV 1079] (1747) – with syntonic-comma adjustment, rendered by Claudi Meneghin (2025)
* [https://www.youtube.com/watch?v=4yetEubmIk0 "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)
* [https://www.youtube.com/watch?v=4yetEubmIk0 "Contrapunctus 11" from ''The Art of Fugue'', BWV 1080] (1742–1749) – rendered by Claudi Meneghin (2024)


Line 1,249: Line 1,281:


=== 21st century ===
=== 21st century ===
; [[Bryan Deister]]
* [https://www.youtube.com/watch?v=SCpbbov1fSQ ''music box 46edo''] (2025)
; [[Jake Freivald]] ([https://soundcloud.com/jdfreivald site])
; [[Jake Freivald]] ([https://soundcloud.com/jdfreivald site])
* [https://soundcloud.com/jdfreivald/a-seed-planted-yet-another ''A Seed Planted - (Yet another version: 46 EDO)''] [http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/a_seed_planted-starling-46-EDO.mp3 play]{{dead link}}  
* [https://soundcloud.com/jdfreivald/a-seed-planted-yet-another ''A Seed Planted - (Yet another version: 46 EDO)''] [http://micro.soonlabel.com/gene_ward_smith/Others/Freivald/a_seed_planted-starling-46-EDO.mp3 play]{{dead link}}  
Line 1,282: Line 1,317:
* [https://www.archive.org/details/Chromosounds ''Chromosounds''] [http://clones.soonlabel.com/public/micro/gene_ward_smith/chromosounds/GWS-GPO-Jazz-chromosounds.mp3 play]
* [https://www.archive.org/details/Chromosounds ''Chromosounds''] [http://clones.soonlabel.com/public/micro/gene_ward_smith/chromosounds/GWS-GPO-Jazz-chromosounds.mp3 play]
* [https://www.archive.org/details/MusicForYourEars ''Music For Your Ears''] [https://www.archive.org/download/MusicForYourEars/musicfor.mp3 play] – The central portion is in [[27edo]]; the rest is in 46edo.
* [https://www.archive.org/details/MusicForYourEars ''Music For Your Ears''] [https://www.archive.org/download/MusicForYourEars/musicfor.mp3 play] – The central portion is in [[27edo]]; the rest is in 46edo.
; [[Tristan Bay]]
* [https://www.youtube.com/watch?v=s61YY80E_IA ''Catalyst''] (2025)
; vivi mouse
* [https://soundcloud.com/vivi-mouse-emoji/valentines-day ''valentine's day''] (2025)


== Notes ==
== Notes ==

Latest revision as of 00:13, 16 August 2025

← 45edo 46edo 47edo →
Prime factorization 2 × 23
Step size 26.087 ¢ 
Fifth 27\46 (704.348 ¢)
Semitones (A1:m2) 5:3 (130.4 ¢ : 78.26 ¢)
Consistency limit 13
Distinct consistency limit 9

46 equal divisions of the octave (abbreviated 46edo or 46ed2), also called 46-tone equal temperament (46tet) or 46 equal temperament (46et) when viewed under a regular temperament perspective, is the tuning system that divides the octave into 46 equal parts of about 26.1 ¢ each. Each step represents a frequency ratio of 21/46, or the 46th root of 2.

Theory

In the opinion of some, 46edo is the first equal division to deal adequately with the 13-limit, though others award that distinction to 41edo or 53edo. 46edo's fifth is slightly sharp of just, which some people (e.g. Margo Schulter) prefer, sometimes strongly, over both the just fifth and fifths of temperaments with flat fifths, such as meantone. Many say that sharp fifths give a characteristic bright sound to 5-limit triads, and consider the sound of meantone triads to be more mellow in comparison. 46edo is not a zeta peak edo, but it is a zeta gap edo. It is distinctly consistent in the 9-odd-limit, and it is consistent to the 13-odd-limit or the no-15 no-19 23-odd-limit.

46edo is also notable for being the smallest equal division to approximate harmonics 3, 5, 7, 11, and 13 with less than 25% relative interval error.

Rank-2 temperaments it supports include sensi, valentine, shrutar, rodan, leapday, and unidec. The 11-odd-limit minimax tuning for valentine, (11/7)1/10, is only 0.01 cents flat of 3\46 octaves.

Shrutar22 as srutis describes a possible use of 46edo for Indian music.

Prime harmonics

Approximation of prime harmonics in 46edo
Harmonic 2 3 5 7 11 13 17 19 23
Error Absolute (¢) +0.0 +2.4 +5.0 -3.6 -3.5 -5.7 -0.6 -10.6 -2.2
Relative (%) +0.0 +9.2 +19.1 -13.8 -13.4 -22.0 -2.3 -40.5 -8.4
Steps
(reduced) 		46
(0) 		73
(27) 		107
(15) 		129
(37) 		159
(21) 		170
(32) 		188
(4) 		195
(11) 		208
(24)
Approximation of prime harmonics in 46edo (continued)
Harmonic 29 31 37 41 43 47 53 59 61
Error Absolute (¢) -12.2 +2.8 +9.5 -11.7 +10.2 +12.8 -12.6 +10.4 +4.9
Relative (%) -46.7 +10.7 +36.5 -44.7 +39.2 +48.9 -48.4 +39.8 +18.6
Steps
(reduced) 		223
(39) 		228
(44) 		240
(10) 		246
(16) 		250
(20) 		256
(26) 		263
(33) 		271
(41) 		273
(43)

Subsets and supersets

46edo can be treated as two circles of 23edo separated by an interval of 26.087 cents.

Intervals

# Cents Approximate ratios[note 1] Ups and downs notation

(EUs: v5A1 and ^^d2)

SKULO notation (K or S = 1, U = 2) Solfege
0 0.0 1/1 perfect unison P1 D Perfect unison P1 D da do
1 26.1 81/80, 64/63, 49/48 up unison ^1 ^D comma-wide unison,
super unison 		K1, S1 KD, SD du di
2 52.2 28/27, 36/35, 33/32 downminor 2nd vm2 vEb subminor 2nd, uber unison sm2, U1 sEb, UD fro ro
3 78.3 25/24, 21/20, 22/21, 24/23, 23/22 minor 2nd m2 Eb minor 2nd,
classic augmented unison 		m2, kkA1 Eb, kkD# fra rih
4 104.3 16/15, 17/16, 18/17 upminor 2nd ^m2 ^Eb classic minor 2nd,
comma-narrow aug unison 		Km2, kA1 KEb, kD# fru ra
5 130.4 13/12, 14/13, 15/14 dupminor 2nd ^^m2 ^^Eb lesser neutral second, augmented unison n2, A1 UEb, D# fri ru[note 2]
6 156.5 12/11, 11/10, 23/21 dudmajor 2nd vvM2 vvE greater neutral second,
super aug unison 		N2, sA1 uE, sD# ri ruh[note 3]
7 182.6 10/9 downmajor 2nd vM2 vE classic/comma-narrow major 2nd kM2 kE ro reh
8 208.7 9/8 major 2nd M2 E major 2nd M2 E ra re
9 234.8 8/7, 23/20 upmajor 2nd ^M2 ^E supermajor 2nd SM2 SE ru ri
10 260.9 7/6 downminor 3rd vm3 vF subminor 3rd sm3 sF no ma
11 287.0 13/11, 20/17 minor 3rd m3 F minor 3rd m3 F na meh
12 313.0 6/5 upminor 3rd ^m3 ^F classic minor 3rd Km3 KF nu me
13 339.1 11/9, 17/14, 28/23 dupminor 3rd ^^m3 ^^F lesser neutral 3rd n3 UF ni mu[note 2]
14 365.2 16/13, 26/21, 21/17 dudmajor 3rd vvM3 vvF# greater neutral 3rd N3 uF# mi muh[note 3]
15 391.3 5/4 downmajor 3rd vM3 vF# classic major 3rd kM3 kF# mo mi
16 417.4 14/11, 23/18 major 3rd M3 F# major 3rd M3 F# ma maa
17 443.5 9/7, 13/10, 22/17 upmajor 3rd ^M3 ^F# supermajor 3rd SM3 SF# mu mo
18 469.6 21/16, 17/13 down 4th v4 vG sub 4th s4 sG fo fe
19 495.7 4/3 perfect 4th P4 G perfect 4th P4 G fa fa
20 521.7 27/20, 23/17 up 4th ^4 ^G comma-wide 4th K4 KG fu fih
21 547.8 11/8 dup 4th ^^4 ^^G uber 4th, sub diminished 5th U4, sd5 UG, sAb fi/sho fu
22 573.9 7/5, 18/13, 32/23 dudaug 4th,
dim 5th 		vvA4, d5 vvG#, Ab classic augmented 4th, diminished 5th kkA4, d5 kkG#, Ab pi/sha fi
23 600.0 17/12, 24/17 downaug 4th, updim 5th vA4, ^d5 vG#, ^Ab comma-narrow aug 4th,
comma-wide dim 5th 		kA4, Kd5 kG#, KAb po/shu seh
24 626.1 10/7, 13/9, 23/16 aug 4th, dupdim 5th A4, ^^d5 G#, ^^Ab augmented 4th,
classic diminished 5th 		A4, KKd5 G#, KKAb pa/shi se
25 652.2 16/11 dud 5th vv5 vvA super augmented 4th,
unter 5th 		SA4, u5 SG#, uA pu/si su
26 678.3 40/27, 34/23 down 5th v5 vA comma-narrow 5th k5 kA so sih
27 704.3 3/2 perfect 5th P5 A perfect 5th P5 A sa sol
28 730.4 32/21, 26/17 up 5th ^5 ^A super 5th S5 SA su si
29 756.5 14/9, 20/13, 17/11 downminor 6th vm6 vBb subminor 6th sm6 sBb flo lo
30 782.6 11/7 minor 6th m6 Bb minor 6th m6 Bb fla leh
31 808.7 8/5 upminor 6th ^m6 ^Bb classic minor 6th Km6 KBb flu le
32 834.8 13/8, 21/13, 34/21 dupminor 6th ^^m6 ^^Bb lesser neutral 6th n6 UBb fli lu[note 2]
33 860.9 18/11, 28/17, 23/14 dudmajor 6th vvM6 vvB greater neutral 6th N6 uB li luh[note 3]
34 887.0 5/3 downmajor 6th vM6 vB classic major 6th kM6 kB lo la
35 913.0 22/13, 17/10 major 6th M6 B major 6th M6 B la laa
36 939.1 12/7 upmajor 6th ^M6 ^B supermajor 6th SM6 SB lu li
37 965.2 7/4, 40/23 downminor 7th vm7 vC subminor 7th sm7 sC tho ta
38 991.3 16/9, 23/13 minor 7th m7 C minor 7th m7 C tha teh
39 1017.4 9/5 upminor 7th ^m7 ^C classic/comma-wide minor 7th Km7 KC thu te
40 1043.5 11/6, 20/11, 42/23 dupminor 7th ^^m7 ^^C lesser neutral 7th, sub diminished 8ve n7, sd8 UC, sDb thi tu[note 2]
41 1069.6 24/13, 13/7, 28/15 dudmajor 7th vvM7 vvC# greater neutral 7th,

diminished 8ve

N7, d8 uC#, Db ti tuh[note 3]
42 1095.7 15/8, 32/17, 17/9 downmajor 7th vM7 vC# classic major 7th,

comma-wide dim 8ve

kM7, Kd8 kC#, KDb to ti
43 1121.7 48/25, 40/21, 21/11, 23/12, 44/23 major 7th M7 C# major 7th,
classic diminished 8ve 		M7, KKd8 C#, KKDb ta taa
44 1147.8 27/14, 35/18, 64/33 upmajor 7th ^M7 ^C# supermajor 7th, unter 8ve SM7, u8 SC#, uD tu to
45 1173.9 160/81, 63/32, 96/49 down 8ve v8 vD comma-narrow 8ve, sub 8ve k8/s8 kD, sD do da
46 1200.0 2/1 perfect 8ve P8 D perfect 8ve P8 D da do

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality Color Monzo Format Examples
downminor zo [a, b, 0, 1> 7/6, 7/4
minor fourthward wa [a, b>, b < −1 32/27, 16/9
upminor gu [a, b, −1> 6/5, 9/5
dupminor ilo [a, b, 0, 0, 1> 11/9, 11/6
dudmajor lu [a, b, 0, 0, −1> 12/11, 18/11
downmajor yo [a, b, 1> 5/4, 5/3
major fifthward wa [a, b>, b > 1 9/8, 27/16
upmajor ru [a, b, 0, −1> 9/7, 12/7

All 46edo chords can be named using ups and downs. Alterations are always enclosed in parentheses, additions never are. Ups or downs immediately after the chord root affect the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Here are the zo, gu, ilo, lu, yo and ru triads:

Color of the 3rd JI Chord Notes as Edosteps Notes of C Chord Written Name Spoken Name
zo 6:7:9 0–10–27 C vEb G Cvm C downminor
gu 10:12:15 0–12–27 C ^Eb G C^m C upminor
ilo 18:22:27 0–13–27 C ^^Eb G C^^m C dupminor
lu 22:27:33 0–14–27 C vvE G Cvv C dudmajor or C dud
yo 4:5:6 0–15–27 C vE G Cv C downmajor or C down
ru 14:18:21 0–17–27 C ^E G C^ C upmajor or C up

For a more complete list, see Ups and downs notation #Chords and chord progressions.

Notation

Ups and downs notation

46edo can be notated with ups and downs, spoken as up, dup, dudsharp, downsharp, sharp, upsharp etc. and down, dud, dupflat etc. Note that dudsharp is equivalent to trup (triple-up) and dupflat is equivalent to trud (triple-down).

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12
Sharp symbol
      
         
    
Flat symbol       
              

Another notation uses alternative ups and downs. Here, this can be done using sharps and flats with arrows, borrowed from extended Helmholtz–Ellis notation:

Step offset 0 1 2 3 4 5 6 7 8 9 10 11 12
Sharp symbol
Flat symbol

Sagittal notation

This notation uses the same sagittal sequence as 39edo.

Evo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8033/32

Revo flavor

Sagittal notationPeriodic table of EDOs with sagittal notation81/8033/32

Approximation to JI

alt : Your browser has no SVG support.
Selected 15-limit intervals approximated in 46edo

17-odd-limit interval mappings

The following tables show how 17-odd-limit intervals are represented in 46edo. Prime harmonics are in bold; inconsistent intervals are in italics.

17-odd-limit intervals in 46edo (direct approximation, even if inconsistent)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
11/7, 14/11 0.117 0.4
9/5, 10/9 0.205 0.8
17/16, 32/17 0.608 2.3
13/7, 14/13 2.137 8.2
13/11, 22/13 2.253 8.6
3/2, 4/3 2.393 9.2
5/3, 6/5 2.598 10.0
17/11, 22/17 2.884 11.1
17/12, 24/17 3.000 11.5
17/14, 28/17 3.001 11.5
11/8, 16/11 3.492 13.4
7/4, 8/7 3.609 13.8
9/8, 16/9 4.786 18.3
5/4, 8/5 4.991 19.1
17/13, 26/17 5.137 19.7
17/9, 18/17 5.393 20.7
17/10, 20/17 5.598 21.5
13/8, 16/13 5.745 22.0
11/6, 12/11 5.885 22.6
7/6, 12/7 6.001 23.0
15/8, 16/15 7.383 28.3
17/15, 30/17 7.991 30.6
13/12, 24/13 8.138 31.2
11/9, 18/11 8.278 31.7
9/7, 14/9 8.394 32.2
11/10, 20/11 8.482 32.5
7/5, 10/7 8.599 33.0
13/9, 18/13 10.531 40.4
13/10, 20/13 10.736 41.2
15/11, 22/15 10.875 41.7
15/14, 28/15 10.992 42.1
15/13, 26/15 12.958 49.7
17-odd-limit intervals in 46edo (patent val mapping)
Interval and complement Error (abs, ¢) Error (rel, %)
1/1, 2/1 0.000 0.0
11/7, 14/11 0.117 0.4
9/5, 10/9 0.205 0.8
17/16, 32/17 0.608 2.3
13/7, 14/13 2.137 8.2
13/11, 22/13 2.253 8.6
3/2, 4/3 2.393 9.2
5/3, 6/5 2.598 10.0
17/11, 22/17 2.884 11.1
17/12, 24/17 3.000 11.5
17/14, 28/17 3.001 11.5
11/8, 16/11 3.492 13.4
7/4, 8/7 3.609 13.8
9/8, 16/9 4.786 18.3
5/4, 8/5 4.991 19.1
17/13, 26/17 5.137 19.7
17/9, 18/17 5.393 20.7
17/10, 20/17 5.598 21.5
13/8, 16/13 5.745 22.0
11/6, 12/11 5.885 22.6
7/6, 12/7 6.001 23.0
15/8, 16/15 7.383 28.3
17/15, 30/17 7.991 30.6
13/12, 24/13 8.138 31.2
11/9, 18/11 8.278 31.7
9/7, 14/9 8.394 32.2
11/10, 20/11 8.482 32.5
7/5, 10/7 8.599 33.0
13/9, 18/13 10.531 40.4
13/10, 20/13 10.736 41.2
15/11, 22/15 10.875 41.7
15/14, 28/15 10.992 42.1
15/13, 26/15 13.129 50.3

Consistent circles

46edo is home to a number of consistent circles, both ones closing after generating all 46 notes and ones closing after generating 23edo.

46-note circles by gen. with related temperaments organized by period
Interval Closing
Error		 Consistency 1\1 1\2
68/65 25.9% Normal Valentine Semivalentine
10/9 36.1% Normal Mitonic Unidec, hendec
31/24 70.2% Weak Sensible, sensi add-31 Bison add-31, bisensi add-31
23-note circles by gen. with related half-octave temperaments
Interval Closing
Error		 Consistency Temperaments
17/16 53.5% Weak Diaschismic
23/21 85.7% Weak Bison
44/39 12.3% Super-strong Abigail
21/17 53.6% Weak ?
14/11 10.2% Super-strong ?
21/16 107% Sub-weak ?

For the 23rd-octave temperament that 46edo supports which combines all above 23-note circles, see icositritonic.

Regular temperament properties

Subgroup Comma list Mapping Optimal
8ve stretch (¢) 		Tuning error
Absolute (¢) Relative (%)
2.3 [73 -46⟩ [⟨46 73]] −0.755 0.75 2.89
2.3.5 2048/2025, 78732/78125 [⟨46 73 107]] −1.219 0.90 3.45
2.3.5.7 126/125, 245/243, 1029/1024 [⟨46 73 107 129]] −0.595 1.34 5.12
2.3.5.7.11 121/120, 126/125, 176/175, 245/243 [⟨46 73 107 129 159]] −0.274 1.36 5.20
2.3.5.7.11.13 91/90, 121/120, 169/168, 176/175, 245/243 [⟨46 73 107 129 159 170]] +0.030 1.41 5.42
2.3.5.7.11.13.17 91/90, 121/120, 154/153, 169/168, 176/175, 245/243 [⟨46 73 107 129 159 170 188]] +0.047 1.31 5.02
2.3.5.7.11.13.17.23 91/90, 121/120, 154/153, 169/168, 176/175, 208/207, 231/230 [⟨46 73 107 129 159 170 188 208]] +0.101 1.23 4.72
  • 46et is lower in relative error than any previous equal temperaments in the 17-, 19-, 23-limit, and others. The next equal temperaments doing better in the aforementioned subgroups are 72, 72, 94, respectively. 46et is even more prominent in the no-19 23-limit, and the next equal temperament doing better in this subgroup is 140.

Commas

This is a partial list of the commas that 46et tempers out with its patent val, ⟨24 38 56 67 83 89].

Prime
limit 		Ratio[note 4] Monzo Cents Color name Name(s)
5 (16 digits) [24 1 -11⟩ 52.50 Salegu Magus comma
5 (14 digits) [13 5 -9⟩ 32.95 Satritrigu Valentine comma
5 2048/2025 [11 -4 -2⟩ 19.55 Sagugu Diaschisma
5 78732/78125 [2 9 -7⟩ 13.40 Sepgu Sensipent comma
5 (14 digits) [9 -13 5⟩ 6.15 Saquinyo Amity comma
7 686/675 [1 -3 -2 3⟩ 27.99 Trizo-agugu Senga
7 245/243 [0 -5 1 2⟩ 14.19 Zozoyo Sensamagic comma
7 126/125 [1 2 -3 1⟩ 13.80 Zotrigu Starling comma
7 1029/1024 [-10 1 0 3⟩ 8.43 Latrizo Gamelisma
7 5120/5103 [10 -6 1 -1⟩ 5.76 Saruyo Hemifamity comma, aberschisma
7 (20 digits) [31 -6 -2 -6⟩ 2.69 Sasa-tribiru-agugu Pessoalisma
7 4375/4374 [-1 -7 4 1⟩ 0.40 Zoquadyo Ragisma
11 121/120 [-3 -1 -1 0 2⟩ 14.37 Lologu Biyatisma
11 176/175 [4 0 -2 -1 1⟩ 9.86 Lorugugu Valinorsma
11 896/891 [7 -4 0 1 -1⟩ 9.69 Saluzo Pentacircle comma
11 385/384 [-7 -1 1 1 1⟩ 4.50 Lozoyo Keenanisma
11 441/440 [-3 2 -1 2 -1⟩ 3.93 Luzozogu Werckisma
13 91/90 [-1 -2 -1 1 0 1⟩ 19.13 Thozogu Superleap comma, biome comma
13 169/168 [-3 -1 0 -1 0 2⟩ 10.27 Thothoru Buzurgisma, dhanvantarisma
13 196/195 [2 -1 -1 2 0 -1⟩ 8.86 Thuzozogu Mynucuma
13 507/500 [-2 1 -3 0 0 2⟩ 24.07 Thothotrigu
13 351/350 [-1 3 -2 -1 0 1⟩ 4.94 Thorugugu Ratwolfsma
13 352/351 [5 -3 0 0 1 -1⟩ 4.93 Thulo Minor minthma
17 256/255 [8 -1 -1 0 0 0 -1⟩ 6.78 Sugu Charisma, septendecimal kleisma
17 289/288 [-5 -2 0 0 0 0 2⟩ 6.00 Soso Semitonisma

Rank-2 temperaments

Periods
per 8ve 		Generator Cents Temperaments MOS scales L:s
1 1\46 26.087 Sfourth
3\46 78.261 Valentine 1L 14s (15-tone)
15L 1s (16-tone)
16L 15s (31-tone) 		4:3 ~ quasi-equal
3:1
2:1 ~ QE
5\46 130.435 Twothirdtonic 1L 8s (9-tone)
9L 1s (10-tone)
9L 10s (19-tone)
9L 19s (28-tone)
9L 28s (37-tone) 		6:5 ~ QE
5:1
4:1
3:1
2:1 ~ QE
7\46 182.609 Minortone / mitonic 1L 5s (6-tone)
6L 1s (7-tone)
7L 6s (13-tone)
13L 7s (20-tone)
13L 20s (33-tone) 		11:7
7:4
4:3 ~ QE
3:1
2:1 ~ QE
9\46 234.783 Rodan 1L 4s (5-tone)
1L 5s (6-tone)
5L 6s (11-tone)
5L 11s (16-tone)
5L 16s (21-tone)
5L 21s (26-tone)
5L 26s (31-tone)
5L 31s (36-tone)
5L 36s (41-tone) 		10:9 ~QE
9:1
8:1
7:1
6:1
5:1
4:1
3:1
2:1 ~ QE
11\46 286.957 Gamity 4L 1s (5-tone)
4L 5s (9-tone)
4L 9s (13-tone)
4L 13s (17-tone)
4L 17s (21-tone)
21L 4s (25-tone) 		11:2
9:2
7:2
5:2
3:2 ~ QE, Golden
2:1 ~ QE
13\46 339.130 Amity / hitchcock 4L 3s (7-tone)
7L 4s (11-tone)
7L 11s (18-tone)
7L 18s (25-tone)
7L 25s (32-tone)
7L 32s (39-tone) 		7:6 ~ QE
6:1
5:1
4:1
3:1
2:1 ~ QE
15\46 391.304 Magus / amigo 1L 2s (3-tone)
3L 1s (4-tone)
3L 4s (7-tone)
3L 7s (10-tone)
3L 10s (13-tone)
3L 13s (16-tone)
3L 16s (19-tone)
3L 19s (21-tone)
3L 21s (24-tone)
3L 24s (27-tone)
3L 27s (30-tone)
3L 30s (33-tone)
3L 33s (36-tone)
3L 36s (39-tone)
3L 39s (42-tone) 		16:15 ~ QE
15:1
14:1
13:1
12:1
11:1
10:1
9:1
8:1
7:1
6:1
5:1
4:1
3:1
2:1 ~ QE
17\46 443.478 Sensi 3L 2s (5-tone)
3L 5s (8-tone)
8L 3s (11-tone)
8L 11s (19-tone)
19L 8s (27-tone) 		12:5
7:5
5:2
3:2 ~ QE, Golden
2:1
19\46 495.652 Leapday 2L 3s (5-tone)
5L 2s (7-tone)
5L 7s (12-tone)
12L 5s (17-tone)
17L 12s (29-tone) 		11:8
8:3
5:3 ~ Golden
3:2 ~ QE, Golden
2:1 ~ QE
21\46 547.826 Heinz 2L 3s (5-tone)
2L 5s (7-tone)
2L 7s (9-tone)
2L 9s (11-tone)
11L 2s (13-tone)
11L 13s (24-tone)
11L 24s (35-tone) 		17:4
13:4
9:4
5:4 ~ QE
4:1
3:1
2:1 ~ QE
2 1\46 26.087 Ketchup
2\46 52.174 Shrutar 2L 2s (4-tone)
2L 4s (6-tone)
2L 6s (8-tone)
2L 8s (10-tone)
2L 10s (12-tone)
2L 12s (14-tone)
2L 14s (16-tone)
2L 16s (18-tone)
2L 18s (20-tone)
2L 20s (22-tone)
22L 2s (24-tone) 		21:2
19:2
17:2
15:2
13:2
11:2
9:2
7:2
5:2
3:2 ~ QE, Golden
2:1 ~ QE
3\46 78.261 Semivalentine 2L 2s (4-tone)
2L 4s (6-tone)
2L 6s (8-tone)
2L 8s (10-tone)
2L 10s (12-tone)
2L 12s (14-tone)
14L 2s (16-tone)
16L 14s (30-tone) 		20:3
17:3
14:3
11:3
8:3
5:3 ~ Golden
3:2 ~ QE, Golden
2:1 ~ QE
4\46 104.348 Srutal / diaschismic 2L 2s (4-tone)
2L 4s (6-tone)
2L 6s (8-tone)
2L 8s (10-tone)
10L 2s (12-tone)
12L 10s (22-tone)
12L 22s (34-tone) 		19:4
15:4
11:4
7:4
4:3 ~ QE
3:1
2:1 ~ QE
5\46 130.435 2L 2s (4-tone)
2L 4s (6-tone)
2L 6s (8-tone)
8L 2s (10-tone)
8L 10s (18-tone)
18L 10s (28-tone) 		18:5
13:5
8:5 ~ Golden
5:3 ~ Golden
3:2 ~ QE, Golden
2:1 ~ QE
6\46 156.522 Bison 2L 2s (4-tone)
2L 4s (6-tone)
6L 2s (8-tone)
8L 6s (14-tone)
8L 14s (22-tone)
8L 22s (30-tone)
8L 30s (38-tone 		17:6
11:6
6:5 ~ QE
5:1
4:1
3:1
2:1 ~ QE
7\46 182.609 Unidec / hendec 2L 2s (4-tone)
2L 4s (6-tone)
6L 2s (8-tone)
6L 8s (14-tone)
6L 14s (20-tone)
20L 6s (26-tone) 		16:7
9:7
7:2
5:2
3:2 ~ QE, Golden
2:1 ~ QE
8\46 208.696 Abigail 2L 2s (4-tone)
4L 2s (6-tone)
6L 2s (8-tone)
6L 8s (14-tone)
6L 14s (20-tone)
6L 20s (26-tone)
6L 26s (32-tone)
6L 32s (38-tone)
6L 38s (44-tone) 		15:8
8:7 ~ QE
8:1
7:1
6:1
5:1
4:1
3:1
2:1 ~ QE
9\46 234.783 Echidnic 2L 2s (4-tone)
4L 2s (6-tone)
6L 4s (10-tone)
10L 6s (16-tone)
10L 16s (26-tone)
10L 26s (36-tone) 		14:9
9:5
5:4 ~ QE
4:1
3:1
2:1 ~ QE
10\46 260.87 Bamity 2L 2s (4-tone)
4L 2s (6-tone)
4L 6s (10-tone)
4L 10s (14-tone)
14L 4s (18-tone)
14L 18s (32-tone) 		13:10
10:3
7:3
4:3 ~ QE
3:1
2:1 ~ QE
11\46 286.957 Vines 2L 2s (4-tone)
4L 2s (6-tone)
4L 6s (10-tone)
4L 10s (14-tone)
4L 14s (18-tone)
4L 18s (22-tone)
4L 22s (26-tone)
4L 26s (30-tone)
4L 30s (34-tone)
4L 34s (38-tone)
4L 38s (42-tone) 		12:11 ~ QE
11:1
10:1
9:1
8:1
7:1
6:1
5:1
4:1
3:1
2:1 ~ QE
23 1\46 26.087 Icositritonic

Scales

Main article: List of MOS scales in 46edo
Sensi
Elfleapday
Elfsensus

Harmonic scales

46edo represents overtones 8 through 16 (written as JI ratios 8:9:10:11:12:13:14:15:16) with degrees 0, 8, 15, 21, 27, 32, 37, 42, 46. This corresponds to scale steps of 8, 7, 6, 6, 5, 5, 5, 4.

  • 8\46 (208.696 ¢) stands in for frequency ratio 9/8 (203.910 ¢).
  • 7\46 (182.609 ¢) stands in for 10/9 (182.404 ¢).
  • 6\46 (156.522 ¢) stands in for 11/10 (165.004 ¢) and 12/11 (150.637 ¢).
  • 5\46 (130.435 ¢) stands in for 13/12 (138.573 ¢), 14/13 (128.298 ¢) and 15/14 (119.443 ¢).
  • 4\46 (104.348 ¢) stands in for 16/15 (111.731 ¢).
Harmonic Note (starting from C)
1 C
3 G
5 E⁠ ⁠
7 G𝄪, B⁠ ⁠
9 D
11 E♯, F⁠ ⁠
13 G♯, A⁠ ⁠
15 B⁠ ⁠

Instruments

Lumatone

Skip fretting

Skip fretting system 46 2 11 is a skip fretting system for playing 46-edo on a 23-edo stringed instrument.


Skip fretting system 46 7 11 is another skip fretting system for 46edo. The examples on this page are for 7-string guitar.

Harmonics

1/1: string 2 open

2/1: string 3 fret 5

3/2: not easily accessible

5/4: string 5 fret 4

Music

Modern renditions

Johann Sebastian Bach
Nicolaus Bruhns
Scott Joplin
  • Maple Leaf Rag (1899) – with syntonic comma adjustment, arranged for harpsichord and rendered by Claudi Meneghin (2024)

21st century

Bryan Deister
Jake Freivald (site)
Andrew Heathwaite
Aaron Krister Johnson
Claudi Meneghin
Herman Miller
Joseph Monzo
Ray Perlner
Gene Ward Smith
Tristan Bay
vivi mouse

Notes

  1. ↑ Based on treating 46edo as a 2.3.5.7.11.13.17.23 subgroup temperament; other approaches are also possible. However, ratios of 15 are not included here, as except for 15/8 and 16/15 themselves 46edo has intervals involving the 15th harmonic poorly approximated in general. This is because, while the 3rd and 5th harmonics are sharp and their deviations from just intonation add up, 7, 11, and 13 are all tuned flat, making the difference even larger. This prevents it from being consistent in the 15-odd-limit, as there is a discrepancy approximating 15/13 and 26/15—9\46 is closer to 15/13 by a hair, but 10\46 represents the difference between 46edo's 15/8 and 13/8 and is more likely to appear in chords actually functioning as 15/13.
  2. ↑ 2.0 2.1 2.2 2.3 /u/ as in supraminor
  3. ↑ 3.0 3.1 3.2 3.3 /ʌ/ as in submajor
  4. ↑ Ratios longer than 10 digits are presented by placeholders with informative hints.
Retrieved from "https://en.xen.wiki/index.php?title=46edo&oldid=207067"