53edo

Prime factorization

53 (prime)

Step size

22.6415¢

Fifth

31\53 (701.887¢)
(convergent)

Semitones (A1:m2)

5:4 (113.2¢ : 90.57¢)

Consistency limit

9

Distinct consistency limit

9

Special properties

zeta peak
zeta peak integer
zeta integral
zeta gap

English Wikipedia has an article on:

53 equal temperament

The famous 53 equal divisions of the octave (53edo), or 53(-tone) equal temperament (53tet, 53et) when viewed from a regular temperament perspective, divides the octave into 53 equal comma-sized parts of around 22.6 cents each.

Theory

53edo is notable as a 5-limit system, a fact apparently first noted by Isaac Newton, notably tempering out the schisma (32805/32768) and the kleisma (15625/15552). More complex 5-limit commas tempered out include the amity comma (1600000/1594323), the semicomma (2109375/2097152), and the vulture comma ([24 -21 4⟩). In the 7-limit it tempers out 225/224, 1728/1715 and 3125/3087, the marvel comma, the gariboh, and the orwell comma. In the 11-limit, it tempers out 99/98 and 121/120 (in addition to their difference, 540/539), and is the optimal patent val for big brother temperament, which tempers out both, as well as 11-limit orwell temperament, which also tempers out the 11-limit commas 176/175 and 385/384. In the 13-limit, it tempers out 169/168, 275/273, 325/324, 625/624, 676/675, 1001/1000, 2080/2079, and 4096/4095, and gives the optimal patent val for athene temperament. It is the seventh strict zeta edo. It can also be treated as a no-elevens, no-seventeens tuning, on which it is consistent all the way up to the 23-odd-limit.

53edo has also found a certain dissemination as an edo tuning for Arabic, Turkish, Persian music.

53edo's step size is sometimes called the "Holdrian comma", despite not being a rational one.

Prime harmonics

Approximation of prime harmonics in 53edo
Harmonic		2	3	5	7	11	13	17	19	23	29	31
Error	absolute (¢)	+0.00	-0.07	-1.41	+4.76	-7.92	-2.79	+8.25	-3.17	+5.69	-10.71	+9.68
Error	relative (%)	+0	-0	-6	+21	-35	-12	+36	-14	+25	-47	+43
Steps (reduced)		53 (0)	84 (31)	123 (17)	149 (43)	183 (24)	196 (37)	217 (5)	225 (13)	240 (28)	257 (45)	263 (51)

Subsets and supersets

53edo is the 16th prime edo, following 47edo and coming before 59edo.

Many of its multiples such as 159edo, 212edo, 742edo, 901edo and 954edo have good consistency limit and are each of their own interest. The mercator family comprises rank-2 temperaments with 1/53-octave periods.

Intervals

#	Cents	Approximate Ratios*	Ups and Downs Notation			Solfeges
0	0.00	1/1	P1	unison	D	Da	Do
1	22.64	81/80, 64/63, 50/49	^1	up unison	^D	Du	Di
2	45.28	49/48, 36/35, 33/32, 128/125	^^1, vvm2	dup unison, dudminor 2nd	^^D, vvEb	Di / Fre	Daw
3	67.92	25/24, 28/27, 22/21, 27/26, 26/25	vvA1, vm2	dud-aug 1sn, downminor 2nd	vvD#, vEb	Fro	Ro
4	90.57	19/18, 20/19, 21/20, 256/243	vA1, m2	downaug 1sn, minor 2nd	vD#, Eb	Fra	Rih
5	113.21	16/15, 15/14	A1, ^m2	aug 1sn, upminor 2nd	D#, ^Eb	Fru	Ra
6	135.85	14/13, 13/12, 27/25	v~2	downmid 2nd	^^Eb	Fri	Ru
7	158.49	35/32, 12/11, 11/10, 57/52, 800/729	^~2	upmid 2nd	vvE	Re	Ruh
8	181.13	10/9	vM2	downmajor 2nd	vE	Ro	Reh
9	203.77	9/8	M2	major 2nd	E	Ra	Re
10	226.42	8/7, 256/225	^M2	upmajor 2nd	^E	Ru	Ri
11	249.06	15/13, 144/125, 125/108	^^M2, vvm3	dupmajor 2nd, dudminor 3rd	^^E, vvF	Ri / Ne	Raw
12	271.70	7/6, 75/64	vm3	downminor 3rd	vF	No	Ma
13	294.34	13/11, 19/16, 32/27	m3	minor 3rd	F	Na	Meh
14	316.98	6/5	^m3	upminor 3rd	^F	Nu	Me
15	339.62	11/9, 243/200	v~3	downmid 3rd	^^F	Ni	Mu
16	362.26	16/13, 100/81	^~3	upmid 3rd	vvF#	Me	Muh
17	384.91	5/4	vM3	downmajor 3rd	vF#	Mo	Mi
18	407.55	19/15, 24/19, 81/64	M3	major 3rd	F#	Ma	Maa
19	430.19	9/7, 14/11	^M3	upmajor 3rd	^F#	Mu	Mo
20	452.83	13/10, 125/96, 162/125	^^M3, vv4	dupmajor 3rd, dud 4th	^^F#, vvG	Mi / Fe	Maw
21	475.47	21/16, 25/19, 675/512, 320/243	v4	down 4th	vG	Fo	Fe
22	498.11	4/3	P4	perfect 4th	G	Fa	Fa
23	520.75	27/20	^4	up 4th	^G	Fu	Fih
24	543.40	11/8, 15/11, 26/19	v~4	downmid 4th	^^G	Fi / She	Fu
25	566.04	18/13	^~4, vd5	upmid 4th, downdim 5th	vvG#, vAb	Pe / Sho	Fuh
26	588.68	7/5, 45/32	vA4, d5	downaug 4th, dim 5th	vG#, Ab	Po / Sha	Fi
27	611.32	10/7, 64/45	A4, ^d5	aug 4th, updim 5th	G#, ^Ab	Pa / Shu	Se
28	633.96	13/9	^A4, v~5	upaug 4th, downmid 5th	^G#, ^^Ab	Pu / Shi	Suh
29	656.60	16/11, 19/13, 22/15	^~5	upmid 5th	vvA	Pi / Se	Su
30	679.25	40/27	v5	down 5th	vA	So	Sih
31	701.89	3/2	P5	perfect 5th	A	Sa	Sol
32	724.53	32/21, 38/25, 243/160, 1024/675	^5	up 5th	^A	Su	Si
33	747.17	20/13, 192/125, 125/81	^^5, vvm6	dup 5th, dudminor 6th	^^A, vvBb	Si / Fle	Saw
34	769.81	14/9, 25/16, 11/7	vm6	downminor 6th	vBb	Flo	Lo
35	792.45	19/12, 30/19, 128/81	m6	minor 6th	Bb	Fla	Leh
36	815.09	8/5	^m6	upminor 6th	^Bb	Flu	Le
37	837.74	13/8, 81/50	v~6	downmid 6th	^^Bb	Fli	Lu
38	860.38	18/11, 400/243	^~6	upmid 6th	vvB	Le	Luh
39	883.02	5/3	vM6	downmajor 6th	vB	Lo	La
40	905.66	22/13, 27/16, 32/19	M6	major 6th	B	La	Laa
41	928.30	12/7	^M6	upmajor 6th	^B	Lu	Li
42	950.94	26/15, 125/72, 216/125	^^M6, vvm7	dupmajor 6th, dudminor 7th	^^B, vvC	Li / The	Law
43	973.58	7/4	vm7	downminor 7th	vC	Tho	Ta
44	996.23	16/9	m7	minor 7th	C	Tha	Teh
45	1018.87	9/5	^m7	upminor 7th	^C	Thu	Te
46	1041.51	64/35, 11/6, 20/11, 729/400	v~7	downmid 7th	^^C	Thi	Tu
47	1064.15	13/7, 24/13, 50/27	^~7	upmid 7th	vvC#	Te	Tuh
48	1086.79	15/8	vM7	downmajor 7th	vC#	To	Ti
49	1109.43	19/10, 36/19, 40/21, 243/128	M7	major 7th	C#	Ta	Tih
50	1132.08	48/25, 27/14, 21/11, 52/27, 25/13	^M7	upmajor 7th	^C#	Tu	To
51	1154.72	96/49, 35/18, 64/33, 125/64	^^M7, vv8	dupmajor 7th, dud 8ve	^^C#, vvD	Ti / De	Taw
52	1177.36	160/81, 63/32, 49/25	v8	down 8ve	vD	Do	Da
53	1200.00	2/1	P8	perfect 8ve	D	Da	Do

* based on interpreting 53edo as a no-17's 19-limit temperament. Italics represent inconsistent intervals which are mapped by the 19-limit patent val to their second-closest (as opposed to closest) approximation in 53edo.

Interval quality and chord names in color notation

Combining ups and downs notation with color notation, qualities can be loosely associated with colors:

Quality	Color	Monzo Format	Examples
downminor	zo	(a, b, 0, 1)	7/6, 7/4
minor	fourthward wa	(a, b) with b < -1	32/27, 16/9
upminor	gu	(a, b, -1)	6/5, 9/5
downmid	ilo	(a, b, 0, 0, 1)	11/9, 11/6
upmid	lu	(a, b, 0, 0, -1)	12/11, 18/11
downmajor	yo	(a, b, 1)	5/4, 5/3
major	fifthward wa	(a, b) with b > 1	9/8, 27/16
upmajor	ru	(a, b, 0, -1)	9/7, 12/7

All 53edo chords can be named using ups and downs. An up, down or mid after the chord root affects the 3rd, 6th, 7th, and/or the 11th (every other note of a stacked-3rds chord 6-1-3-5-7-9-11-13). Alterations are always enclosed in parentheses, additions never are.

Here are the zo, gu, ilo, lu, yo and ru triads:

Color of the 3rd	JI Chord	Notes as Edosteps	Notes of C Chord	Written Name	Spoken Name
zo	6:7:9	0-12-31	C vEb G	Cvm	C downminor
gu	10:12:15	0-14-31	C ^Eb G	C^m	C upminor
ilo	18:22:27	0-15-31	C ^^Eb G	Cv~	C downmid
lu	22:27:33	0-16-31	C vvE G	C^~	C upmid
yo	4:5:6	0-17-31	C vE G	Cv	C downmajor or C down
ru	14:18:21	0-19-31	C ^E G	C^	C upmajor or C up

For a more complete list, see Ups and downs notation #Chords and Chord Progressions.

Notation

Sagittal

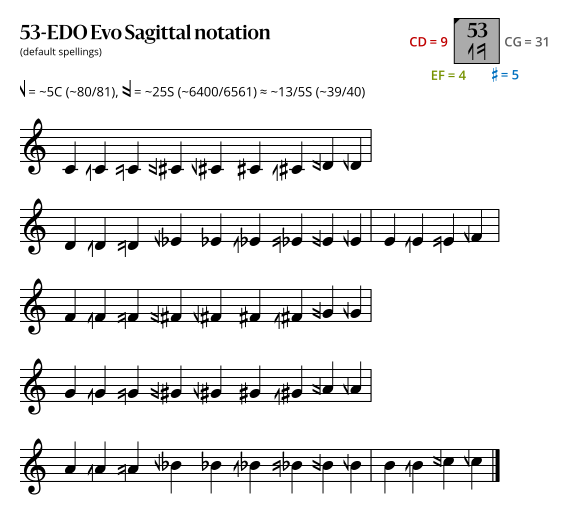
The following table shows sagittal notation accidentals in one apotome for 53edo.

Steps	0	1	2	3	4	5
Symbol

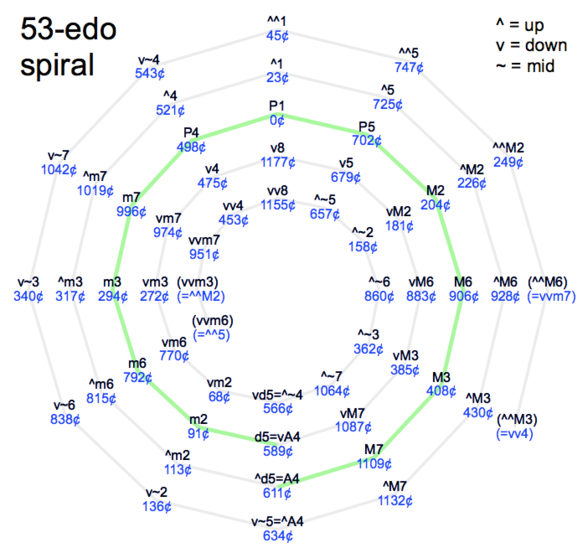
Relationship to 12edo

Whereas 12edo has a circle of twelve 5ths, 53edo has a spiral of twelve 5ths (since 31\53 is on the 7\12 kite in the scale tree). This shows 53edo in a 12edo-friendly format. Excellent for introducing 53edo to musicians unfamiliar with microtonal music. The two innermost and two outermost intervals on the spiral are duplicates.

JI approximation

53edo provides excellent approximations for the classic 5-limit just chords and scales, such as the Ptolemy-Zarlino "just major" scale.

Interval	Ratio	Size	Difference
Perfect fifth	3/2	31	−0.07 cents
Major third	5/4	17	−1.40 cents
Minor third	6/5	14	+1.34 cents
Major second	9/8	9	−0.14 cents
Major second	10/9	8	−1.27 cents
Minor second	16/15	5	+1.48 cents

Because the 5th is so very accurate, 53edo also offers good approximations for Pythagorean thirds. In addition, the 43\53 interval is only 4.8 cents wider than the just ratio 7/4, so 53edo can also be used for 7-limit harmony, tempering out the septimal kleisma, 225/224.

15-odd-limit interval mappings

The following table shows how 15-odd-limit intervals are represented in 53edo. Octave-reduced prime harmonics are bolded; inconsistent intervals are in italic.

15-odd-limit intervals by direct mapping (even if inconsistent)
Interval, complement	Error (abs, ¢)	Error (rel, %)
3/2, 4/3	0.068	0.3
9/8, 16/9	0.136	0.6
9/5, 10/9	1.272	5.6
15/13, 26/15	1.316	5.8
5/3, 6/5	1.340	5.9
13/10, 20/13	1.384	6.1
5/4, 8/5	1.408	6.2
15/8, 16/15	1.476	6.5
13/9, 18/13	2.655	11.7
13/12, 24/13	2.724	12.0
13/8, 16/13	2.792	12.3
7/4, 8/7	4.759	21.0
7/6, 12/7	4.827	21.3
9/7, 14/9	4.895	21.6
13/11, 22/13	5.130	22.7
7/5, 10/7	6.167	27.2
15/14, 28/15	6.235	27.5
15/11, 22/15	6.445	28.5
11/10, 20/11	6.514	28.8
13/7, 14/13	7.551	33.3
11/9, 18/11	7.785	34.4
11/6, 12/11	7.854	34.7
11/8, 16/11	7.922	35.0
11/7, 14/11	9.961	44.0

15-odd-limit intervals by patent val mapping
Interval, complement	Error (abs, ¢)	Error (rel, %)
1/1, 2/1	0.000	0.0
3/2, 4/3	0.068	0.3
9/8, 16/9	0.136	0.6
9/5, 10/9	1.272	5.6
15/13, 26/15	1.316	5.8
5/3, 6/5	1.340	5.9
13/10, 20/13	1.384	6.1
5/4, 8/5	1.408	6.2
15/8, 16/15	1.476	6.5
13/9, 18/13	2.655	11.7
13/12, 24/13	2.724	12.0
13/8, 16/13	2.792	12.3
7/4, 8/7	4.759	21.0
7/6, 12/7	4.827	21.3
9/7, 14/9	4.895	21.6
13/11, 22/13	5.130	22.7
7/5, 10/7	6.167	27.2
15/14, 28/15	6.235	27.5
15/11, 22/15	6.445	28.5
11/10, 20/11	6.514	28.8
13/7, 14/13	7.551	33.3
11/9, 18/11	7.785	34.4
11/6, 12/11	7.854	34.7
11/8, 16/11	7.922	35.0
11/7, 14/11	12.681	56.0

Regular temperament properties

Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Tuning Error
Subgroup	Comma List	Mapping	Optimal 8ve Stretch (¢)	Absolute (¢)	Relative (%)
2.3	[-84 53⟩	[⟨53 84]]	+0.022	0.022	0.10
2.3.5	15625/15552, 32805/32768	[⟨53 84 123]]	+0.216	0.276	1.22
2.3.5.7	225/224, 1728/1715, 3125/3087	[⟨53 84 123 149]]	-0.262	0.861	3.81
2.3.5.7.11	99/98, 121/120, 176/175, 2200/2187	[⟨53 84 123 149 183]]	+0.248	1.279	5.64
2.3.5.7.11.13	99/98, 121/120, 169/168, 176/175, 275/273	[⟨53 84 123 149 183 196]]	+0.332	1.183	5.22
2.3.5.7.11.13.19	99/98, 121/120, 169/168, 176/175, 209/208, 275/273	[⟨53 84 123 149 183 196 225]]	+0.391	1.105	4.88

53et is lower in relative error than any previous equal temperaments in the 3-, 5-, and 13-limit. The next equal temperaments doing better in these subgroups are 306, 118, and 58, respectively. It is even more prominent in the 2.3.5.7.13.19 and 2.3.5.7.13.19.23 subgroups, and the next equal temperament doing better in either subgroup is 130.

Linear temperaments

Table of rank-2 temperaments by generator
Periods per 8ve	Generator	Cents	Associated Ratio	Temperament
1	2\53	45.28	36/35	Quartonic
1	5\53	113.21	16/15	Misneb
1	7\53	158.49	11/10	Hemikleismic
1	9\53	203.77	9/8	Baldy
1	10\53	226.42	8/7	Semaja
1	11\53	249.06	15/13	Hemischis / hemigari
1	12\53	271.70	7/6	Orson / orwell
1	13\53	294.34	25/21	Kleiboh
1	14\53	316.98	6/5	Hanson / catakleismic / countercata
1	15\53	339.62	11/9	Amity / houborizic
1	16\53	362.26	16/13	Submajor
1	18\53	407.55	1225/972	Ditonic / coditone
1	19\53	430.19	9/7	Hamity
1	21\53	475.47	21/16	Vulture / buzzard
1	22\53	498.11	4/3	Helmholtz / garibaldi / pontiac
1	25\53	566.04	18/13	Tricot
1	26\53	588.68	45/32	Untriton / aufo