User:Eboone/EDO Impressions
PROGESS REPORT, so you don't have to scroll:
Changed the scope of the project to go only up to 50edo, instead of 72edo
Everything up to 20edo is complete, though is certainly subject to change. The 20edo and 22edo demos also available. Tier placements for every other edo are now accurate, though may change.
Start date: May 13, 2024. Most recent update: November 19, 2024.
—————————

I, at least currently, work strictly in edos. I tend not to venture higher than 53edo in my own works, and for reasons that are explained in Overarching Points > Multiples of EDOs, I consider 50edo to be the largest edo that interests me. So, this page will go over my general thoughts regarding every positive integer edo up to that point. There are also a few smackdowns between edos that I consider "arch rivals," with the first being between 17edo and 19edo.
A few edos on this page are so intriguing that I (will soon) have entirely separate pages talking about them. These pages are linked directly below the headings of these edos.
Of course, all tier lists and impressions on this page are subject to change in the future.
All demos are short loops at 120bpm created by me in MuseScore 3.
Overarching Points
After working on this project for about a month, I realized there were many points I found myself repeating. This isn't inherently an issue, but I thought it would make more sense if I sectioned off a few points that apply to multiple edos. I will be referencing these points directly in the descriptions of many edos, so it may be wise to read them before continuing.
Approximating Just Intonation
My introduction to microtonality was the harmonic series. One of the properties of the harmonic series is that intervals found closer to the fundamental tend to be more resonant, i.e. they are consonant by definition. Consonance is a very desirable property for any given temperament to have, as it is the basis for making music sound "pleasant." Of course, there are plenty of mathematically consonant intervals that can be treated as dissonances — such as 7/5 and 16/15 — but even these intervals have that unmistakable resonant quality that makes them "easier" to listen to.
Keep in mind, I'm using quotation marks a lot because all of this is largely subjective. If you want to use extreme intervals with no shred of consonance, feel free to do that. It's just generally desirable to have access to consonant intervals because of their beauty and versatility.
Intervals of certain prime limits have their own flavors of resonance, like how 5/4 and 6/5 "lock in" in a similar fashion that is recognizable as 5-limit resonance. This, among other reasons, is why it is useful to analyze edos in terms of their abilities to approximate certain prime limits.
I say "approximate" because it is impossible for any regular temperament to perfectly represent more than one prime limit exactly (due to the fact that all prime numbers are coprime with each other). In the case of edos, the only prime limit that is uncompromised is the 2-limit, which grants the substantial ability to make use of perfect octaves. Maintaining the perfect octave is seen as a first priority in most cases due to the concept of octave equivalence, so any other prime limit can only ever be approximated when using edos.
Lower prime limits are generally seen as more important, especially the 3-limit. The perfect fifth is absolutely paramount to the structure of Western music because 1) it is very well approximated in 12edo and 2) it is the generator for the diatonic scale. So, edos with poor approximations of the 3rd harmonic are generally at a disadvantage in terms of versatility and resonance. 5-limit systems are also very desirable, as are 7-limit, 11-limit, and 13-limit systems. I don't usually care for an edo's ability to approximate anything past that.
In short, edos with more consonant intervals are at a distinct advantage compared to other edos. That certainly doesn't mean there won't be any exceptions, but it is true in many cases.
Multiples of EDOs
Looking at the tier list, you may wonder why 12edo is at the top if its multiples are simply the same temperament but with more options. There are a few reasons for this, and it all comes down to the appeals of using smaller edos in general. Here are some of those appeals.
Fewer Notes, Easier
This isn't always the case, but it generally is. One of the primary appeals of edos in general is their convenience and versatility, especially in comparison to just intonation. The extreme end of this is very small edos, and as you venture into larger edos, their compactness becomes less important as they strive to be closer to just intonation. Essentially, a small edo that works very well in a certain JI subset (such as 12edo) gains less from being multiplied, as the amount of new notes isn't justified by a newfound ability to approximate JI.
For example, 72edo does a much better job in the 2.3.5.7.11 subgroup than 12edo, but now you have to deal with 72 notes. At that point, why not just use just intonation?* The smallest example of this is 10edo being placed above 20edo.
*I understand the rationale behind using very large edos instead of just intonation. It isn't just about approximating ratios; there are also things like mosses to consider. I, however, am not in the crowd that uses very large edos. At a certain point (in my opinion, 50 notes to be exact), the sheer amount of notes is enough to tank any other possible advantages of using a particular edo. This segues nicely into the next point:
The Novelty of Fewer
Yeah, I'm literally just saying smaller edos are cooler (unless they're too small; see F tier). I mean, think about it. Equally dividing the octave seems to clash with the logarithmic nature of the harmonic series, so the fact that this even works at all is already cool enough. Yet, all you need are 12 equal partitions to completely dominate the music industry. Sure, your ears may not care about the novelty factor of using a small number of notes within the uncountably infinite realm of pitch, but conceptually I find it incredibly neat.
5edo is a great example. Like, really? Only 5? But it sounds so cute! Then there's 7edo, a surprisingly versatile temperament that often gets me thinking "wait... there's only 7 notes here?" It's kind of like my brain is drawing parallels from the idea of simple ratios being consonant. In a way, small edos are "consonant" and large edos are "dissonant" in terms of their conception.
All You Need
At the end of the day, use whatever tuning you need to achieve your musical vision. It just happens that I basically never consider very large edos to be necessary. If all I need is 12, then all I need is 12. No need to use 24 or 36 or whatever if those extra notes won't help me hone in on the emotions I plan to engender in the listener.
Summary of Ranking
In general, edos with these qualities will place higher on the tier list:
- Versatile
- Few Notes
- Consonant
- Unique
These are just guidelines that I tend to follow, and they in no way provide a concrete method of objectifying edos. However, knowing what I'm looking for will greatly aid in understanding why I place certain edos where I do. For example, 41edo is certainly on the larger side, yet it still resides in S tier because it's just so consonant. It really puts into perspective just how consonant it is if I'm willing to place it that high in spite of the amount of notes.
Plus, these aren't the only guidelines. MOS scales are also considered, especially if they are scales that I find particularly interesting. This is largely subjective, as I really have no way of classifying mosses in any sort of objective way. Factors are also considered, as the factors of an edo determine a lot about its structure. Certain intervals that are technically dissonant may also greatly contribute to an edo's high rating, such as the major third in 17edo (foreshadowing). At the end of the day, everything on this page is based on my own recreational research and opinions, so I'm sorry if your favorite edo is in D tier simply because it doesn't meet my criteria for what makes an edo desirable.
In terms of the actual ranks, I think of B tier as the default, meaning I automatically assume that any given edo is going to be good before I experiment with it. If it turns out to be totally outclassed by edos that are obviously better, it goes in F tier or D tier. If it's pretty useful every once in a while, it goes in C tier. If it has exceptional ethereality, versatility, uniqueness, etc., it goes in A tier or S tier.
Categorization
The 7 Categories of EDOs
I have split edos into 7 distinct categories based on step size:
- 1-4edo — Trivial (300-1200¢)
- 5-9edo — Macrotonal (133.33-240¢)
- 10-14edo — Macro-Semitonal (85.71-120¢)
- 15-19edo — Micro-Semitonal (63.16-80¢)
- 20-29edo — Macro-Diesitonal (41.38-60¢)
- 30-39edo — Micro-Diesitonal (30.77-40¢)
- ≥40edo — Commatonal (≤30¢)
These terms are not standard in any way. I just made them up. Also, I am aware that "macrotonal" generally refers to any temperament whose step size is larger than 100¢. That is not necessarily the meaning here.
Why Categorize EDOs?
The main reason I wanted to split these edos into categories was so that this wiki page wouldn't be an absolutely mammoth wall of text on mobile (which ended up happening anyway, but oh well). Plus, it just felt like a fun challenge.
But why by step size? EDOs are generally distinguished by their intervals, so wouldn't it make sense to group edos by similar interval content? Sure, but how would you actually do that? There would be so much overlap that any and all meaningful distinction between categories would be lost. 29edo, 41edo, and 53edo would be grouped together as Pythagorean systems, but 41edo and 53edo would also be grouped with 31edo and 50edo as 5-limit systems, and 31edo and 50edo would be grouped with 36edo and 72edo as septimal systems, and 72edo would be grouped with 24edo and 26edo as undecimal systems...
As you can see, that falls apart quickly (as does attempting to group edos by factors or mosses or anything else, for the same reason), meaning the only other option is to categorize edos by step size. This is a great option because the size of an edo's step is what dictates its voice leading capabilities. For example, chromatic motion in 12edo is limited to semitones, whereas 31edo allows for movement by diesis. Also, no more extreme overlap between categories; 12 is similar to 11 and 13, and 31 is similar to 30 and 32. The borders between categories may be fuzzy, but that's to be expected when categorizing tuning systems anyway, since harmony itself is fuzzy by nature.
In terms of the actual categories themselves, I essentially divided them by significantly different interval regions, and then into smaller subcategories. There are 4 overarching categories: macrotonal, semitonal, diesitonal, and commatonal, but these still feel too large and contain vastly different edos within themselves. So, I basically just split each category down the middle.
Trivial
These edos are characterized by the fact that they are all subsets of 12edo. This means that, along with being incredibly situational, they also aren't xenharmonic. 1edo in particular raises the question of what a tuning system even is, since it only has one note (assuming octave equivalence).
All 4 of these edos are best used sparingly, as they do not provide much in the way of melodic/harmonic capabilities.
1edo
No prime factorization, 1° = 1200¢, No fifth
Tier: F
Honestly, can this one even be called an edo? I mean, "equal divisions of the octave" implies that the octave is divided. On top of that, since octave equivalence is almost always assumed, this "temperament" literally only has one note. Anyway, this edo is pretty lame because the whole point of using different temperaments is to access different melodic and harmonic opportunities, and this edo doesn't allow any of that. The only way to make this edo musical is through rhythm, dynamics, form, etc... stuff that isn't related to tuning.
These factors alone make this edo terrible, but that doesn't mean you can't make it work. Technically, there is some room for "melodic" expression if you allow yourself to use devices such as pitch bend. Or, perhaps you could use timbres that don't exactly settle on one pitch but clearly aren't unpitched either, like an old guitar string with wobbly harmonics. These "cheat codes" are partially what make one-note jazz solos so interesting, but of course the rest of the interest comes from the novelty of playing only one note amidst an electron cloud of dissonance.
If we were to view this edo as being the first in the set of all positive integer edos, we could say it "introduces" the idea of pitch classes, thus establishing octave equivalence for all edos to come. While it is somewhat neat to view edos as entries in a sequence, it's probably more useful to view them in isolation, which leaves this edo with essentially nothing. At least it's better than 0edo.
2edo
Prime, 1° = 600¢, No fifth
Tier: F
This edo is literally just a tritone, but in this case it's a rather interesting one. It's the 600¢ hemioctave tritone, the only one that is its own octave complement. So, while its melodic and harmonic capabilities in isolation are pretty bare, its symmetrical nature allows for some cool gimmicks. If instead it were, say, 11/8, that would open the possibility of using both 11/8 and 16/11, its octave complement. This would allow for greater melodic and harmonic expression, but at the expense of having a neat symmetrical tritone.
To illustrate this tritone's nature, the demo for this edo is completely flipped on its head. If you listen carefully, you will notice that the pizzicato violins and celli play each other's parts upside down in the second half of the loop. The gimmick is that this only affects contour, not the harmony. So yeah, that's pretty cool.
One interesting property of this edo that cannot be overlooked is the fact that it is prime. The fundamental theorem of arithmetic states that all integers greater than 1 can be represented as a unique product of prime numbers, which applies in this context because we're dealing with positive integer edos. EDOs with lots of prime factors have more opportunities for symmetry within the octave. In this case, 2edo's symmetrical tritone is inherited by all 2n-edos, essentially splitting them down the middle.
Anyway, it's just a tritone. And in fact, I can't honestly say this edo is any better than 1edo. In theory, there should be no reason to choose 1edo over 2edo, but how much does that one extra note really add in practice? At the end of the day, both edos are mere novelties.
3edo
Prime, 1° = 400¢, No fifth
Tier: F+
This edo is just an augmented triad, but specifically one that is derived by stacking three 400¢ major thirds. This means it closes the octave and, as such, is its own inversion. So, once again, the melodic and harmonic capabilities of this triad in isolation are pretty slim compared to, say, one derived by stacking 5/4. Yet, the symmetrical nature of this chord allows for quite a "sturdy" sound that helps to keep the temperament together.
The major third itself is 13.79¢ sharp of 5/4, enough for noticeable inharmonicity to occasionally take place in timbres with a prominent 5th harmonic (such as a piano). This contributes to the "foggy" sound of the temperament, as the demo illustrates. I could say a lot more about this particular major third, but that's really all that matters in the context of 3edo.
The uninvertible nature of the augmented triad is illustrated in the synth, as it oscillates between two inversions of the triad yet the quality of the chord remains utterly identical. If it were any other type of augmented triad, the inversions would still sound quite similar but they would each have a different vibe.
Anyway, I'd say this edo is definitely more interesting than 1edo and 2edo, mostly because it is the smallest edo with a triad.
4edo
2², 1° = 300¢, No fifth
Tier: F+
While I wouldn't necessarily say 2edo is a better version of 1edo, I will say 4edo is a better version of 2edo. It's a diminished tetrad, but specifically one that is derived by stacking four 300¢ minor thirds. This means it closes the octave and, as such, is its own inversion. So, as always, the melodic and harmonic capabilities of this tetrad in isolation are pretty slim compared to, say, one derived by stacking 6/5. Yet, the symmetrical nature of this chord allows for quite a, dare I say, "sturdy" sound that helps to keep the temperament together... how familiar.
The minor third is sat between 6/5 and 32/27, giving it a mildly dark sound that is quite apt for the diminished tetrad. It's a powerful minor third, but without the 5-limit resonance of 6/5. Overall, a great minor third.
I'd say this edo is on equal footing with 3edo, maybe slightly behind. You could certainly argue that it's better than 3edo, considering it contains 2 interlocked instances of 2edo, as well as an extra note. I, however, think augmented triads are more interesting than diminished tetrads in isolation. It's really all about taste, as is everything in the world of music.
Trivial EDO Recap

These first four edos are honestly just memes, so no amount of good things I say about them can eke them out of F tier. I can't really hear them as anything other than subsets of 12edo, which really makes them seem pointless. They work best as additional colors in larger edos that contain them, not as temperaments on their own.
Also, about the whole symmetry thing. EDOs 2-4 are notable for their symmetrical nature, which I pass off as a mere gimmick. The reason I don't find this more interesting is because symmetry in music tends to be boring, especially in terms of form. I prefer music that wanders off into its own realm, rather than music that remains stagnant the entire time. Essentially, if I were to listen to a piece in 4edo, I would get really sick of hearing the same exact diminished chord.
Macrotonal
Now we're getting into edos that people actually care about. 2 new prime edos are introduced here, and they both have unique sounds that carry over into their multiples, making them unmistakable. We also see the introduction of scales here, as the trivial edos have step sizes too wide to be considered scales, in my opinion.
There is still one subset of 12edo left to cover here, and it is unfortunately extremely situational. The rest of the edos, on the other hand, may surprise you with their versatility.
5edo
Prime, 1° = 240¢, Fifth = 720¢ (3\5)
Tier: B-
This is the first edo with a perfect fifth, coming in 18.04¢ sharp of 3/2. Because of how sharp the fifth is, 5edo works best in timbres with quick decay (like a marimba), so that the dissonance of the fifth is softened. It has quite a desirable "uplifting" quality that brings it out amidst the texture of the rest of the scale.
This edo also features interseptimal intervals, a very interesting class of intervals characterized by toeing the lines between extreme septimal intervals. There's the 240¢ "second-third," which lies between 8/7 and 7/6, and the 960¢ "seventh-sixth," which lies between 7/4 and 12/7. I'd say 240¢ definitely sounds more like a supermajor second than an inframinor third in this edo, and I find it almost impossible to hear 960¢ as a sixth since it's so close to the 7th harmonic, but it is interesting how these intervals are technically ambiguous.
Oh yeah, did I just mention it has a decent approximation of the 7th harmonic? It's only 8.83¢ flat of 7/4, which is cool because this approximation extends to all 5n-edos. Anyway, the equipentatonic scale that this edo sports is a bit reminiscent of the minor pentatonic scale of 12edo (or, dare I say, the dorian pentatonic scale), making it quite familiar to unaccustomed ears, but still with a tang of xen. In many cases, it is rather difficult to notice if a piece is in this edo if you aren't familiar with it. Because of this, I'd say 5edo is a good starting edo when venturing into xen territory.
The problem with this edo is the lack of harmonic expression. There really aren't any triads to work with, since there isn't a convincing third. Instead, everything is secundal or quartal (or their inversions). This means 5edo is not very versatile in the slightest, but does provide an intriguing color to use in larger 5n-edos.
Overall, this is pretty fun edo to work in. Melodies here always have a really fun sound no matter how hard you may try to make something sinister. Plus, the fact that this is the only edo with a scale but no convincing thirds is a rather interesting property. It forces you to hone in on nontonal musical factors such as rhythm, dynamics, and form, which I find quite valuable considering how easy it is to hyperfocus on harmony in larger edos. With all that being said, however, I really can't put this edo any higher than B tier because of how non-versatile it is.
6edo
2×3, 1° = 200¢, No fifth
Tier: D
Of the subsets of 12edo, I'd say this is the most interesting because it contains a whole tone, and it's the only one that isn't just a meme. 6edo contains 2 interlocked instances of 3edo, meaning it has the same echoey major third, and it also contains 3 interlocked instances of 2edo, meaning it has the same uninvertible tritone. The combination of these intervals really contributes to the infamous dreamy quality of this edo, better known as the whole-tone scale.
There are many pieces that make use of the whole-tone scale, but very few that exist strictly in 6edo. Claude Debussy is well known for his use of the scale, and it's a very interesting color to use while working in 6n-edos, but a very limiting scale to use in isolation. The best 6edo pieces I could find are the prelude and invention from Aaron Andrew Hunt's The Equal Tempered Keyboard, and they are pretty interesting for what they are. They don't really sound dreamy, which is the sound that I feel is most well suited for this edo, but they are actually able to guide the listener on a comprehensive harmonic journey which is certainly no easy task.
6edo is the first edo to contain a dominant 7th chord, which would be more interesting if there were a perfect fifth, but at least you can resolve it through the back door (up a whole step). In fact, that's really one of the only ways to make satisfying chord progressions in this edo. The arguably more infamous Mario cadence (♭VI-♭VII-I) is ever-present here, as it is, in my opinion, the most satisfying progression that exists in this edo. So, if you really wanted to, you could create a Mario-style fanfare using just the whole-tone scale, but deliberately avoiding the perfect fifth in such a style would be uncharacteristic.
Anyway, it's just the whole-tone scale. I can't reasonably put it in F tier with the rest of the 12edo subsets, since it is an actual scale rather than just an interval or chord, but there's still only one sound I find this edo to be useful for. Plus, there are other edos that do the dream sound much better in my opinion.
7edo
Prime, 1° = 171.43¢, Fifth = 685.71¢ (4\7)
Tier: A-
This is the first edo with a perfect fifth and a third. The fifth is pretty flat, coming in 16.25¢ flat of 3/2, and the third is a supraminor third of 342.86¢. In a way, 7edo is the polar opposite of 5edo, containing a fifth that is almost equally off in the opposite direction. This gives 7edo a noticeably less uplifting sound, and more of a "crying out in pain" sound as one of my subscribers put it. Quartal and quintal structures have a distinct "underwater" quality, as opposed to the skyward energy of such structures in 5edo.
The equiheptatonic scale that this edo sports is a bit reminiscent of the dorian scale of 12edo, but not really. The 2nd, 3rd, 6th, and 7th are all neutral, so this edo has a very distinct xen sound. These neutral intervals, along with the rather sour fourth and fifth, have a very intense sound on an acoustic piano, which is why I elected to use electric piano and synth pads in the demo. 7edo also works very well in tinky percussive timbres, like handpan or kalimba. These sorts of sounds are heard in Fuschiamarine by Sevish, a very high quality example of what this edo is capable of.
This is also the first edo that contains multiple different meaningful scales (ones with at least 5 notes). It contains the basic form of pentic (2L 3s), as well as the hard form of 1L 4s. The basic form of antimachinoid (1L 5s) is also present here, which can be seen as a rather crude tempering of Tetracot[6]. This is a pretty interesting scale, in that it's essentially a compressed whole-tone scale where one of the steps is larger than the others. The equiheptatonic scale itself can be seen as an equal-tempered Tetracot[7], which is surely a bonus for the tetracot fans out there.
It's honestly incredible what this edo can do with so few notes. I often find myself hearing more notes than there actually are, as its very easy for my brain to hear major and minor even when everything is neutralized. 7edo has a tendency to sound like a joke, but has the ability to be extremely powerful. Toccata for Organ by Neil Thornock is another fantastical specimen of this temperament.
Overall, this edo may not be very versatile harmonically, but its sound is truly something to behold, and a sound that cannot be easily replicated in other non-7n-edos. A very nice blend of xen, ease of use, and ethereality. It's also trivially easy to notate, which is always a bonus.
8edo
2³, 1° = 150¢, "Fifth" = 750¢ (5\8)
Tier: B-
This is... an interesting one. Honestly, I really didn't used to like 8edo, but eventually I came to see how powerful it is when used in certain contexts. It doesn't have a perfect fifth or a whole tone, but it is extremely close to 12/11 equal step tuning, meaning it responds well to octave stretching. It also features a good approximation of 13/10, a rather ambiguous "third-fourth" that can either be used as an ultramajor third or a very flat fourth.
Octave stretching is a technique commonly employed in edos with intervals that consistently undershoot certain desirable intervals. In the case of 8edo, 1 degree falls flat of 12/11 by 0.64¢, so by stretching the octave by 5.1¢, you can achieve perfect 12/11 equal step tuning. Of course, this will cause noticeable inharmonicity to occur with octaves, but you could argue that such an effect serves the temperament quite well.
Cadences in this temperament are relatively satisfying, but not in a traditional sense. The 150¢ neutral second can function cadentially either as a wide semitone or a narrow whole tone, meaning cadences tend to feel a bit obtuse or acute, if you will. It's an intriguing motion that sets the harmony of this edo apart from pretty much any other edo, even other 8n-edos. It's a very foreboding motion that of course must be accentuated by a pipe organ and battle-ready percussion.
8edo contains 2 interlocked instances of 4edo, meaning it houses the familiar diminished tetrad. And, just like in 4edo, the diminished/minor sound is what tends to sound the most appealing here since the 450¢ Barbados third really isn't a stable point of rest. This is mainly why I used to think 8edo wasn't very good, since the room for harmonic expression without the major/minor third dichotomy just seemed bland. Plus, the only stable sounds being a minor chord with an omitted fifth and a diminished chord just didn't seem very appealing.
But, as you can hopefully hear in the demo, I believe to have found the perfect sound for this temperament. It was somewhat inspired by Aaron Andrew Hunt's "Fantasia & Fugue a4 in 8ET", once again from The Equal Tempered Keyboard, another piece I find quite fascinating. Other neat environments for 8edo include, as always, the percussive style characteristic of Hideya's music, another one of my favorite xen composers. Like Ensor's paintings is a very cool example of what 8edo sounds like in a strictly melodic context. It's, as Hideya says, an unpleasant experience that really gets you thinking for some reason.
Overall, a bit of a niche edo, but the sounds it produces are ineffable. I found myself struggling to place 8edo on the tier list, because the utter absence of a perfect fifth isn't something to just gloss over, yet its inquisitive properties certainly warrant a placement above 6edo and the melodic nature of the neutral second puts it on par with 7edo. So, I just placed it in B tier, above 5edo.
9edo
3², 1° = 133.33¢, Fifth = 666.67¢ (5\9)
Tier: A
9edo is the first edo with 2 flavors of thirds. It is notable for its uncanny approximations of septimal intervals down to a fraction of a cent. These intervals have an almost ghostly quality to them, giving this edo an incredibly unique, resonant sound that other edos of this scale simply cannot match. For example, the juxtaposition of the 266.67¢ subminor third (nearly exactly 7/6) and the 400¢ major third (the one from 3edo) is totally jarring. The incredibly acrid fifth also contributes to the general vibe of resonant septimal consonances battling against sour dissonances. It's an ineffable combination of opposing stimuli, giving this edo an unmistakable sound.
9edo is also the first edo to support mavila temperament, being one of 3 that support it natively in the patent val. It's certainly an extreme tempering, but making the fifth any sharper would get rid of the septimal consonances, so this particular way of approaching mavila is truly unique.
As this edo is right on the border of what I consider to be the macrotonal edos, 1 degree of 9edo has a particular quality to it that makes it sound like a semitone in some contexts and a neutral second in other contexts. My piece Elegy of the Willow illustrates this by including many chromaticisms, sometimes in the context of a chromatic scale and sometimes in the context of cadential motion.
Other inspiring works in this temperament include Buttered Cat Paradox by Xolta and Caelum by miaxia. Caelum especially illustrates the nature that I've described, leading me to believe 9edo works best in such a style. The demo I wrote for this edo, however, is nowhere near the style of any of these pieces, yet I think it works quite well. The aforementioned "ghostly" quality of 9edo, particularly in the fifth, gives the tango an "abandoned" quality that would fit well in a old lost town, like the Hidden Village from The Legend of Zelda: Twilight Princess.
Overall, a very unique edo. You can choose to avoid the dissonant fifth or embrace it, with both approaches leading to an incredible sound. It's surprisingly versatile, more so than any edo smaller than it, putting it above 7edo.
Macrotonal EDO Recap

These edos are very cool and interesting. Just because they don't have very many notes doesn't necessarily mean they are limiting. Even 5edo, the most limiting of them all, has much room for expression through its interseptimal intervals. 9edo is especially intriguing to me, as it is the smallest edo with 2 flavors of thirds, making it the first edo to allow for any sort of complex chord movement. It is a beautiful edo that ends up being more versatile than you'd think, along with 7edo and even 8edo.
If you're in the market for edos that approximate simple ratios very well, you won't find much here unless you're looking for something like 9edo. The main appeal here is how compact these edos are, and it's just really neat to think that you don't even need 12 notes to make awesome music.
Oh, and I just realized I have barely talked about notation! Fortunately, all five of these edos are relatively easy to notate. 5edo and 9edo are notable in this regard; 5edo can be notated pentatonic-wise on a 5-line staff by skipping B and F, and 9edo can be notated with either harmonic or melodic mavila accidentals. I prefer to preserve the harmonic integrity in mavila systems; I embrace the quirk of having reversed sharps and flats so I don't have to deal with F♭ being a perfect fifth above B. 6edo can be notated as a subset of 12edo, 7edo can be notated by simply using all seven naturals, and 8edo can be notated as a subset of 24edo with quarter-tone accidentals. As you will see with future edos, however, things may not be as simple.
Macro-Semitonal
These are the first edos with what I would consider semitones, meaning voice leading possibilities are about to blow wide open. 12edo is also here, but I won't be saying much about it.
10edo
2×5, 1° = 120¢, Fifth = 720¢ (3\5)
Tier: A+
Ah yes, the homeland of mosh (3L 4s). 10edo is actually my favorite of the edos less than 12, though 9edo does come pretty close. This edo is the largest one with a singular third, that being the 360¢ submajor third which is extremely close to 16/13. That means this temperament also features a stunning approximation of the 13th harmonic, coming in just 0.53¢ sharp. It also features all of the interseptimal intervals from 5edo, meaning it includes the same approximation of the 7th harmonic, as well as a relatively stable fifth (especially compared to 9edo).
10edo is a very xen tuning — more so than even 7edo in my opinion — because it doesn't even pretend to represent the diatonic scale. Instead, as mentioned previously, the heptatonic mos of 10edo is 3L 4s, or mosh. This is an incredibly intriguing mos that can be difficult to wrap your head around, but the sounds it produces are quite beautiful. Apartment in the Sky by HEHEHE I AM A SUPAHSTAR SAGA is an example of the brightest mode of mosh, dril.
The demo I wrote for this edo is in the middle mode, bish. It oscilates between "tonic" and "dominant," and it sounds quite reminiscent of such movement in the diatonic mos, until you realize it's totally different. This mode of mosh could be mapped to the double harmonic major scale in a diatonic system, yet doing that results in a very different sound. I was incredibly surprised when I retuned the demo to be in A♭ double harmonic major, only to be subjected to something the original could only dream of being as weird as. Of course, I probably only say that because I wasn't used to it.
Being the first edo with what I would consider a semitone, chromatic movement in this edo is relatively familiar, yet with a tang of xen. In fact, that's a fairly apt way of describing this temperament as a whole. The third feels like a major third sometimes, especially when combined with the 1080¢ major seventh, yet other times it feels totally neutral or even minor. It certainly doesn't feel minor in isolation, but it kinda does at some points in the demo. This supposed submajor third is even more ambiguous than the 240¢ second-third, which is literally ambiguous by definition.
Notating this edo is an interesting challenge. I choose to notate it with the seven naturals assigned to mosh, with A dril lying on the naturals, but this certainly isn't standard. The "standard" (if you can call it that) is to notate this edo pentatonic-wise, using ups and downs to reach the notes in between. I, however, am not a particular fan of ups and downs. I prefer sagittal, but even that looks a bit clunky in this edo. The problem is the fact that B and F are skipped when using this method, or that B=C and E=F. I just think that looks and feels weird to read because it's based on the diatonic mos which 10edo doesn't have.*
Instead, it makes much more sense to assign the naturals to mosh and use sharps and flats to reach the notes in between. Or, you could use diamond-mos notation, which is what Apartment in the Sky is notated in. My problem with this system is how difficult it is to actually implement, plus the idea of transposing a score instead of using key signatures is not my style. I'd rather just write in the accidentals manually than transpose the entire score, unless it's an extreme case.
Anyway, notation aside, this edo has such an amazing sound. Every 5n-edo (especially those up to 30edo) has a particular 5n-edo sound, yet this edo stands out even among that group. Being the largest edo with a singular third, it really cant help but sound totally xen, even though its semitone step-size tends to make it sound almost like 12edo in certain cases. Mosh is a super cool landscape, but as Adam Neely shows in "How to make Microtonal Lo-Fi Hip Hop," you can just as easily stick to the 2 interlocked equipentatonic scales and produce some great music.
Overall, a very unique and awesome edo that stands atop the macrotonal podium as the best edo smaller than 12edo (in my opinion).
*This problem creeps up in all 5n-edos up to 30edo, and while I say I prefer to assign the naturals to a different mos rather than stick to the diatonic mos which isn't even supported, I really only mean that for 10edo. 15edo is the other most common 5n-edo with the 720¢ fifth, and trying to notate it any other way than with accordance to the diatonic mos ends up looking weird. At the end of the day, some edos just aren't fit to be notated on a 5-line staff generated by fifths.
11edo
Prime, 1° = 109.09¢, Fifth = 654.55¢ (6\11)
Tier: C+
This is a... fun one. It suffers from being almost 12edo, giving it a somewhat similar vibe to 9edo, but without the whole "battle between consonance and dissonance" thing since nearly everything here is dissonant. The fifth is more like 16/11 than anything close to 3/2, meaning it actually has the worst fifth since 6edo, though 8edo comes close. This edo is notable for its approximation of 9/7, being just 1.28¢ sharp, making it the first edo with a supermajor third. It also has a pretty good approximation of the 11th harmonic, being 5.87¢ flat.
While 10edo is the home of mosh, 11edo is the home of smitonic (4L 3s). I don't really like it as much as mosh, but it has its uses. Anyway, I don't really dabble with smitonic in this edo. I prefer to write free of any scale, since this edo is already pretty limiting as it is. That's why the demo is full of jazz chords.
As always, The Equal Tempered Keyboard has some good examples of this edo. They're rather beautiful for what they are, but I find myself wishing they were in a different edo. Tostadosto by Francium and Longwayaway People by Sevish are other great examples of what this edo is capable of.
The best way to notate this edo is as a subset of 22edo, which also isn't doing it any favors. Overall, a niche edo with an alien sound that I just cannot find myself wanting to use very often. Its approximation of the 11th harmonic is somewhat appealing, and the "almost 12edo" quality can make for some interesting effects, but there are better edos for both of these things (spoiler alert).
12edo
2²×3, 1° = 100¢, Fifth = 700¢ (7\12)
Tier: S+
I could say many things about 12edo, but I don't think you need to hear it. It's the first edo with the diatonic mos, the first edo with a decent approximation of 3/2 (1.96¢ flat), and the first edo that can claim to be a 5-limit system. It's a meantone temperament, but only a little. This means the thirds are closer to pure 5-limit ratios, but not enough to sacrifice the edo's ability to support Pythagorean melodies. It contains symmetrical augmented and diminished structures, as well as the whole-tone scale. It's essentially a perfect temperament that works well in basically any style, so I cannot honestly put it anywhere but the top of the tier list.
Yeah, that's all I'm going to say about 12edo. The purpose of this page is really to delve into the other edos.
13edo
Prime, 1° = 92.31¢, Dual Fifths = 738.46¢ (7\13), 646.15¢ (6\13)
Tier: B+
This is just a better 11edo. It has a better approximation of 11/8 (2.53¢ sharp), and is honestly much better at pulling off the "almost 12edo" effect. It also has 2 fifths, and even though they're both terrible it's still better than having whatever 11edo has.
13edo features 3 very nice mosses in their basic forms. Gramitonic (4L 5s) is an absolutely amazing enneatonic mos that makes use of dual fifths. Oneirotonic (5L 3s) is an octatonic mos that also takes advantage of the dual fifths, and can be seen as an extension of the diatonic scale. Archaeotonic (6L 1s) is a heptatonic mos that resembles 7edo if the small step is large enough. The support for these really good mosses in their basic forms is amazing.
The sostenuto of Easley Blackwood Jr.'s Twelve Microtonal Etudes for Electronic Music Media illustrates the vibe of the "almost 12edo" effect very well, evoking a "sinking" quality. I've also heard 13edo described as having a "jealous" sound, which is fairly apt. The intervals themselves contribute to these traits as well. The minor third is only slightly sharp of 7/6, and the major third is actually submajor with how flat it is of 5/4. These two thirds have such a unique aura that I cannot describe. They, along with the two fifths as well as the 11/8 (and 13/8) come together to create a truly profound temperament.
Still not A tier, though. The problem is that the fifths are so sour, and that they have no other redeeming qualities other than there being 2 of them. 9edo also has a rather extreme fifth, but its "battle between consonance and dissonance" thing is definitely cool enough to boost it. 13edo doesn't have the same effect, since the most resonant interval here is the 11/8 approximation, nowhere near the capabilities of 9edo. Everything is just dissonant.
So yeah, this edo has some pretty cool properties. I just don't find myself wanting to use it very often. It's quite situational, but its support for mosses definitely makes it cool enough for B tier.
14edo
2×7, 1° = 85.71¢, Fifth = 685.71¢ (4\7)
Tier: A
This is the first edo with 3 flavors of thirds. The neutral third is the same one from 7edo, the minor third is a rather flat subminor third (almost inframinor), and the major third is a nice supermajor third that comes in just a few cents flat of 9/7. This is a pretty wide spread, allowing for great contrast between different chord qualities.
Being a low 7n-edo, the apotome is tempered out. This makes sense in 7edo, since there simply aren't enough notes for there to be anything close to a semitone, but in the case of 14edo, it's quite intriguing. You could create a "diatonic" scale, but it would either end up equalized or with more than 2 step sizes. In fact, this edo doesn't have any heptatonic mosses. Instead, it features the likes of semiquartal (5L 4s) and lime (4L 6s), both in their basic forms. These mosses are rather interesting, with semiquartal being somewhat popular (especially in 19edo). The one example of lime in 14edo that I could find is Rexasaurus by Francium.
Notating 14edo presents similar problems to that of 10edo. Instead of having to battle the whole B=C and E=F thing, now the issue is the fact that sharps and flats have no meaning. Since the apotome is tempered out, G♯ is literally the same pitch as G. To get around this, most people would just use ups and downs, but I already said I don't really like ups and downs. So, I prefer sagittal. It's a bit clunky since this edo officially uses the Athenian 55/54 symbol instead of something from the Spartan set, but it works well enough.
Anyway, this edo is underappreciated in my opinion. It inherits the xen quality of 7edo and places it in an environment with many more opportunities. My favorite piece in this edo is the prelude from The Equal Tempered Keyboard, and I don't think it would've sounded any better in a different temperament. The watery fifth when paired with the extremely flat subminor third has such a bittersweet sound, and when paired with the supermajor third it has a particular nostalgic vibe. And, of course, the neutral third has its own character that is completely separate from the other two thirds. To think that such a breadth of emotions can be achieved with so few notes is honestly beautiful (ignoring 12edo).
I wish I could say more about 14edo, but I really don't have that much experience in it. On the surface, it seems like a pretty weird tuning since it does a horrible job of approximating pretty much any prime harmonics, which is why I haven't used it much. But, in the future, I do wish to use it in a variety of styles to see what it is truly capable of.
Macro-Semitonal EDO Recap
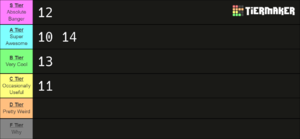
A mix of really good and... decent... edos. I'd say 11edo is a bit of an outlier here, even though it is quite similar to 13edo, since I see it as being totally outclassed. Although, perhaps you could use both 11edo and 13edo in conjunction to create some cool effects, as Claudi Meneghin did in his Micropiece in 11edo & 13edo. Either way, a pretty niche use case for two pretty niche edos.
Anyway, those two are clearly not my favorites. 14edo is, as I said, totally underappreciated and underexplored. It can create some truly ethereal sounds on par with 9edo, which is why I put them right next to each other on the tier list. I don't like saying xen temperaments are good for "alien" music, but 14edo really does hit the mark in this regard (as is seen in the glorious thumbnail of Warp Drive by JUMBLE).
10edo is one of my favorite edos. I'd like to have a custom 10edo marimba, if that's even a feasible project. It's a great edo for tuning your ears to the world of xenharmony without just being a 5-limit system like 19edo or 31edo, because of its familiar semitone size. It's honestly one of the most underrated edos in existence, since even 5edo gets more attention than it.
And then there's 12edo. Pretty good, I'd say.
Micro-Semitonal
All 5 of these edos are amazing. Even 18edo ended up growing on me and climbing its way into A tier, putting every single edo here above B tier.
A few of these are very popular, and a few of these are criminally underexplored. You've probably already seen your fair share of music in 17edo and 19edo, but the other 3 are absolutely incredible as well.
15edo
3×5, 1° = 80¢, Fifth = 720¢ (3\5)
Tier: S-
This is probably the most popular 5n-edo, and for good reason. It's like 12edo from an alternate universe; it has two flavors of thirds and a reasonable fifth, yet it also has decent approximations of 7/4 and 11/8 and it doesn't support the diatonic scale. It also doesn't really have what I would call a whole-tone. Instead, it has the interseptimal second-third from 5edo, along with a neutral second and a small semitone. These three step sizes provide a vast array of melodic possibilities, allowing you to create powerful melodies that have no analog in the diatonic scale.
The minor third is only 4.36¢ sharp of 6/5, meaning this edo has a better approximation of this ratio than every smaller edo, and it really shines when paired with the sharp fifth. It's a very pure sound, even though the fifth is pretty far off of 3/2. The major third is the same as in 12edo, but the major seventh is sharp thanks to the fifth. This means major seventh chords have a very bright quality that really accentuates the uplifting nature of the fifth. Overall, the minor and major thirds have very different vibes, and they both react with the fifth in unique ways.
15edo supports the porcupine and blackwood temperaments, with the pine (7L 1s) and pentawood (5L 5s) mosses being present in their basic forms. Both of these mosses are rather interesting, but I prefer to work freely of any particular scale. The three vastly different step sizes really shine when used in conjunction. The second-third especially brings a lot to the table, since it can function either as a second or a third. Xênerie by Woyten illustrates this quite well, using it to create an inframinor sound as well as using it as a supermajor second in the melody.
Like Satie by Hideya is another great piece in this edo, illustrating the characteristic "out of tune" vibe very well. Incidentally, 15edo works great in a lofi environment. Anyway, I just went with a simple groove for this one. I wanted to accentuate the bass melody, so you can really hear how the different step sizes work together. It uses all three step sizes, as well as the undecimal superfourth approximation, which really adds a layer of grit to the end of the loop. The superfourth honestly feels totally different from everything else in the edo, but perhaps that's just the nature of it.
Suite for Guitar in 15-Note Equal Tuning by Easley Blackwood is probably my favorite piece in this edo. I have nothing to say about it, I just thought I'd mention it. Overall, this is a stellar edo. It is the next smallest edo after 12edo that I am confident placing in S tier, albeit in the lower half. The sheer amount of possibilities with this few notes is honestly amazing.
16edo
2⁴, 1° = 75¢, Fifth = 675¢ (9\16)
Tier: A+
This edo is often said to be the optimal tuning for mavila temperament, and I agree. It is one of three edos that natively support it in the patent val, and I do honestly believe it does it better than the other two. Mavila is a very interesting temperament, pushing the fifth so flat that harmony is literally flipped on its head. It can create some intriguing harmonic effects, sounding like the diatonic scale until suddenly it totally doesn't. I illustrated this in the demo with a shocking E minor chord (sounding E♭ major ish) in the 6th bar, resolving to a totally different key. It never really deviates from the antidiatonic scale, at least not in a way that I would note as significant.
Anyway, the intervals in this edo are very nice. The minor third is the same as in 12edo, but the major third is 11.31¢ flat of 5/4, giving the temperament a distinct somber quality. There is also a fairly good approximation of 7/4, being only 6.17¢ sharp. I've never heard a piece in this edo that I would describe as "joyous" or any other discrete happy adjective. There's always a tinge of solemnity, especially in the andantino of Twelve Microtonal Etudes for Electronic Music Media. It's an unmistakable sound.
16edo is the basis of Armodue theory, which I don't really know much about, but it is based on the mavila superdiatonic (7L 2s) scale. The superdiatonic scale is an enneatonic mos that behaves somewhat similarly to oneirotonic, in that it has two fifths and a flat major third. Having two fifths is pretty cool, but in the case of 16edo, the dual sharp fifth is so sharp that I wouldn't even consider it a fifth.
This edo also works well in a blues context, somewhat surprisingly. Don't Take Five by Woyten is a prime example of this, being one of the coolest pieces I've heard in this edo behind the Blackwood etude. 16edo is honestly underexplored; it has so much potential in a ton of different genres, yet I feel that people are deterred by the fifth and other dissonant intervals. The antidiatonic scale works amazingly in its soft form, which is why I think this is the best tuning for mavila. It's like 9edo, but in exchange for the profound war between consonance and dissonance, you get a somewhat nicer fifth and a somber vibe that is difficult to emulate in other edos. That may not seem like a fair trade since I hyped up 9edo so much, but it makes 16edo much more versatile and interesting.
Overall, an incredible edo deserving of high A tier. I wouldn't say it's better than 10edo, but I know that's just my personal taste holding it back.
17edo
Prime, 1° = 70.59¢, Fifth = 705.88¢ (10\17)
Tier: S
17edo is the first edo after 12edo to have the diatonic scale, and it is the first that demonstrates superpythagorean temperament, though many would say it is better described as a parapythagorean temperament. It sports the hard diatonic scale, where the large step is 3 degrees and the small step is 1 degree. This gives melodies a noticeably more "closed in" sound, whereas meantone temperaments make the diatonic scale more open.
The thirds in this temperament are subminor, neutral, and supermajor, with the neutral third being quite close to 11/9 (5.53¢ sharp). The septimal thirds are actually closer to noble thirds, which are somewhat close to 13/11 and 14/11. I am a big fan of the thirds in 17edo because they aren't as extreme as more pure septimal thirds; they form a nice middle ground. The seconds are also very nice. The diatonic semitone being so flat makes diatonic voice leading feel very locked in, the neutral second just sounds great, and the whole tone is slightly sharp of 9/8, juxtaposing with the subminor second and providing variety.
17edo features mosh in its soft form and gramitonic in its hard form. This means 17edo features my entire top 3 favorite mosses, which is absolutely fabulous. I do prefer softer forms of gramitonic (particularly those found in 22edo, 31edo, and 53edo), but it's still great that it's here. Plus, it's always great to experiment with hard and soft forms of mosses.
The first time I encountered this edo, it was placed next to its arch rival in the same style. I thought it was pretty obvious that 17edo sounded worse, but that's because it was played in a piano timbre. Sure, it can sound quite beautiful in a piano timbre, as shown in The Bedoginning by Woyten (one of my favorite pieces), but have a listen to the acoustic version of the con moto of Twelve Microtonal Etudes for Electronic Music Media, arranged by Matthew Sheeran. When I showed this to my fellow musician brother who had little experience with microtonal music, he literally thought it was in 12edo even after I told him it wasn't. Even I had a hard time telling until the middle section (1:42 in the video) began and I heard that diatonic semitone.
This edo really lends itself well to music that I can only describe as "bouncy," like the Blackwood etude. I feel that meantone temperaments suffer in this regard, while pythagorean and superpyth temperaments thrive. Overall, this is one of my absolute favorite edos, and one that I will surely continue to use in the future. But will it win against its meantone rival in a smackdown?!
18edo
2×3², 1° = 66.67¢, Dual Fifths = 733.33¢ (11\18), 666.67¢ (5\9)
Tier: A
18edo is also known as the third-tone system because one step is exactly equal to one third of a whole-tone in 12edo. It sits in an interesting position, not being too similar to any edos around it. It inherits the subminor and major thirds from 9edo, along with a supraminor third. It also has two fifths that are almost equidistant from 3/2, making it a much more convincing dual fifth system than 13edo.
The acoustic version of the allegro of Twelve Microtonal Etudes for Electronic Music Media is one of my favorite pieces in 18edo. It's a very hectic piece that really taps into the dissonant nature of the temperament. 3 Bagatelles by norokusi is another absolutely beautiful piece (pieces?) that demonstrates this temperament wonderfully. It's honestly haunting, almost to the degree of 9edo...
...this is a segment that was edited at a future time. What I originally explained here is that I feel 9edo is superior to 18edo because of the idea that fewer notes is better. I believed this until I heard Supahstar Saga's arrangement of Aquatic Ambience from Donkey Kong Country. The tight voicings in the electric piano at bar 27 made me realize just how much the in-between notes really add to this edo. I also rediscovered my love for oneirotonic upon hearing this, certainly placing it among my top 5 favorite mosses.
So yeah, it's better than 9edo, but only marginally. In fact, they are positioned right next to each other in A tier, where they will likely remain for the foreseeable future. Whereas 9edo is perfect for creating a sort of "ghostly" sonic landscape, 18edo seems to be perfect for dissonance in general. I realize that's a bit of a bold, sweeping claim, but I suppose that's just because I'm not articulating myself correctly. This edo has such a distinct aura that just gives it a wonderful dissonant sound that I cannot really put into words.
Anyway, 18edo is really cool. It's kind of like a mix of 12edo and 13edo, if that makes sense. It's like 13edo in that it supports oneirotonic and has a similar dissonant vibe, but it contains many structures found in 12edo due to their shared factors. This edo certainly has a lot of potential.
19edo
Prime, 1° = 63.16¢, Fifth = 694.74¢ (11\19)
Tier: S
19edo is the next edo after 17edo to have the diatonic scale, and it is the first that really demonstrates meantone. Specifically, it is very close to 1/3-comma meantone with eigenmonzo 6/5, so the minor third of this edo is only 0.15¢ flat of 6/5. This is the best approximation of 6/5 among all non-19n-edos on this page. The approximation of 5/4 is also relatively decent, coming in 7.36¢ flat. This particular flat major third has a marvelous quality (pun intended), as it comes extremely close to 56/45. It's a very distinct and beautiful major third that really makes this edo shine.
The fifth is also quite marvelous (pun still intended), as it comes extremely close to 112/75. These "marvelous" intervals truly define how this edo feels in the 5-limit, giving it a sound that, in a way, feels even purer than 5-limit just intonation. The soft diatonic scale also melds very well with these slightly flat intervals, giving the temperament a nostalgic quality.
Now.. the septimal intervals. If you just look at 19edo as a 5-limit system, then it is absolutely amazing and certainly rivals 12edo and 31edo. But that isn't all we have here. There are septimal intervals too, and they are... intriguing. It took a while for them to grow on me, but if you stop trying to hear them as perfect approximations of 7/6, 9/7, 7/4 etc. (which they absolutely aren't), their true beauty begins to shine through. To put it generally, you must hear this edo for what it is, rather than for what it is not.
Anyway, the subminor third is even flatter than the one in 14edo, landing right in the middle of the interseptimal region between 9/7 and 7/6. In fact, I'd say it's an inframinor third. Likewise, the supermajor third lands right in the interseptimal region between 9/7 and 21/16, albeit closer to 9/7. The inframinor third really doesn't have a septimal sound at all, and neither does the abysmal approximation of the 7th harmonic (21.46¢ flat), but the supermajor third does come close enough to 9/7 for it to have a septimal quality. The thing is, it's even sharper than the septimal supermajor third, which is already a bit of an extreme sound to get used to, so it ends up being a harsh sound in certain contexts.
With that being said, these intervals are still beautiful. This is technically the first edo with a harmonic 7th chord, and even though it really doesn't sound a whole lot like 4:5:6:7 because of how bad the approximation of the 7th harmonic is, it still has a unique and interesting sound with a warm quality. Plus, it still works better than the native dominant 7th chord in terms of voice leading. The inframinor third is a bit reminiscent of the interseptimal second-third in 5n-edos, but without nearly as much ambiguity about whether it's a second or a third.
Also, something that is easily overlooked in meantone temperaments is how they soften dissonant intervals. Sunrise by HEHEHE I AM A SUPAHSTAR SAGA (an absolutely beautiful piece) illustrates this in the 2nd bar with a spicy B♭maj7(♯11,♯15) chord, yet it doesn't sound spicy at all (to me) because the augmented fifteenth is stretched compared to, say, 12edo. Prelude for playing No. 1 by Tapeworm Saga also shows many of the capabilities of 19edo, even implementing some undecimal harmony.
Oh, and this edo doesn't just feature the diatonic mos. It also features semiquartal in its hard form, a rather popular mos (especially in this edo). I don't really mess with it, but it is there. Anyway, this edo is absolutely amazing for lofi. It doesn't have the same sort of "out of tune" vibe as 15edo, but the unique way this edo handles the 5-limit works very well in the style.
That's why I went with a lofi beat for the demo, which illustrates pretty much everything I mentioned. The 2nd bar features a CM7(9,𝄪11), showing how the supermajor third can light up a chord even when it's not built from the root. The 4th bar features a Dh7(♭9,13), showing how the interseptimal harmonic 7th chord sounds with extensions. The 6th bar features a G♭M7(♯9,13), a chord that sounds way different and much more dissonant in 12edo because of the augmented triad buried within the structure. The seventh bar features an absolutely ethereal F♭(9,11), which is basically just the first five notes of the F♭ major scale, so it would definitely sound much more dissonant in 12edo (especially with the eleventh in the melody).
Anyway, that's 19edo. Love it or hate it, it is a truly stunning edo that stands alone in its field until 31edo shows up. But will it win against its superpyth rival in a smackdown?!
17edo vs 19edo Smackdown
Alright, time for the smackdown. Just looking at how much I wrote, it seems like I'll be handing it to 19edo, but 17edo definitely isn't done here. Let's see what happens if I swap the edos for the demos I wrote!
Since 17edo is superpyth and 19edo is meantone, I couldn't exactly translate between the two seamlessly, preserving the notation. Sometimes I prioritized voice leading, and sometimes I prioritized the nature of the harmony, whether that meant totally altering the quality of a chord or not.
17edo demo retuned
I'm just going to be honest, this is blatantly worse. Some of the voice leading doesn't really translate, particularly in the case of sus4 voicings. In 17edo, C is 1 degree above B, but in 19edo, they are 2 degrees apart, so the falling melody in the left hand of the piano loses some of its effect in the 19edo version. Bar 5 really does open up in this version, with the minor third being so much higher than in 17edo, but I can't really say that's a good thing. It's not bad, but I definitely prefer the darker quality of the noble minor third over the classic minor third in this particular context.
Bar 4 is totally ruined. It's meant to feel like a monster coming from the floor and dragging you down into G minor through strange, dissonant voice leading, and 17edo nails this perfectly. 19edo fails on the 2nd beat because of the ridiculously pure D major triad being used in place of the D neutral triad in the original. There really isn't any better substitute, so this is a sound that 19edo simply cannot emulate. 17edo wins this round!
19edo demo retuned
Perhaps it's unfair that I chose a style that works well in literally any edo, because this actually sounds very good. The previous demo is in a minor key, so 19edo sounds more open (and thus uncharacteristic, in my opinion), whereas this one is in a major key, so 17edo sounds more open. And I must say, something really is lost when attempting to translate 19edo's 5-limit consonances into whatever 17edo is. It just feels less locked in; it's a bit more "gritty." It still sounds really cool, but the marvelousness of 19edo really aids this track more than the crudeness of 17edo. In other words, we're looking for consonant dissonances, not just dissonances.
The magic of bar 7 is totally stripped away, because whereas 19edo softens the minor ninth dissonance between the third and eleventh, 17edo accentuates it. Bar 4 also sounds way different, because the chord itself is way different. What used to be a Dh7(♭9,13) is now a Dnm7(⌄9,13), and although the neutral chord does sound pretty cool, I prefer the harmonic 7th. Bar 2 loses its ethereality because the extreme supermajor third is replaced with the more tame noble major third. And, in general, the voice leading just feels less satisfying when the step size is larger.
With that being said, however, the 17edo version definitely doesn't sound nearly as bad as the 19edo metal. The noble major third is an entire quarter-tone wider than the marvelous major third, giving the 17edo version a totally different sound that really can't be emulated in 19edo. Still, I do prefer the original for the way it softens the dissonant intervals, so 19edo wins this round!
Verdict
Of course, retuning two 8-bar loops isn't going to decide which edo is better. This is just a fun experiment I thought I'd do, and I must say that 19edo wins this smackdown! While the lack of neutral intervals is certainly a bit of a tank, the utter beauty and ethereality of 19edo is something that is truly unique. Not even 31edo can sound like it, thanks to the interseptimal intervals. Anyway, there really isn't a way to compare these in any objective sense because they're so different. They are both absolutely amazing edos considering their size!
By the way, this isn't the only showdown. Stay tuned... (pun intended)
Micro-Semitonal EDO Recap

Three S tier edos in one category! All five of these edos are amazing for their own reasons. 15edo has a particular "living" quality that makes it great for lofi and Gymnopédie-style pieces. Like Satie by Hideya illustrates this quality quite well, and I will likely experiment with this sort of sound myself. 16edo is just amazing, evoking beautiful solemnity and bittersweetness that I cannot overstate. 18edo is its own thing entirely, sounding similar to 9edo but with more options for complex harmony. It's an incredibly potent edo that works extremely well in contexts that you would never expect.
Then there's 17edo and 19edo, two of the most common edos to get people introduced into xenharmony. Supahstar Saga's "Exploring 19-TET" series is a brilliant introduction to 19edo that I would honestly recommend for anyone just getting into the realm of xenharmonic edos. I'm almost tempted to make my own series talking about various edos (if you're from the future and I have already done this, hi), sort of like this page you're reading but in video form so it's easier to digest.
I absolutely love the way 17edo's superpyth/parapyth hybrid flavor affects melodies. I generally prefer harder forms of the diatonic scale, so 19edo often feels too soft for me, but 17edo is just perfect. It lends itself very well to more extreme modes, like lydian and phrygian.
19edo on the other hand, while softer than 17edo, is absolutely amazing in the 5-limit. The interseptimal intervals add so much on top of it as well, making it an absolutely fascinating edo that even 31edo struggles to emulate.
Macro-Diesitonal
20edo
2²×5, 1° = 60¢, Fifth = 720¢ (3\5)
Tier: A
placeholder
21edo
3×7, 1° = 57.14¢, Fifth = 685.71¢ (4\7)
Tier: A
placeholder
22edo
2×11, 1° = 54.55¢, Fifth = 709.09¢ (13\22)
Tier: S
placeholder
23edo
Prime, 1° = 52.17¢, Fifths = 678.26¢ (13\23), 730.44¢ (14\23)
Tier: C
placeholder
24edo
2³×3, 1° = 50¢, Fifth = 700¢ (7\12)
Tier: B
placeholder
25edo
Tier: B+
5², 1° = 48¢, Fifth = 720¢ (3\5)
26edo
2×13, 1° = 46.15¢, Fifth = 692.31¢ (15\26)
Tier: S-
placeholder
27edo
3³, 1° = 44.44¢, Fifth = 711.11¢ (16\27)
Tier: A+
placeholder
28edo
2²×7, 1° = 42.86¢, Fifth = 685.71¢ (4\7)
Tier: C+
placeholder
29edo
Prime, 1° = 41.38¢, Fifth = 703.45¢ (17\29)
Tier: A-
placeholder
Macro-Diesitonal EDO Recap
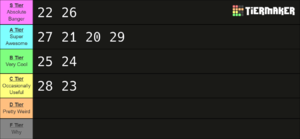
placeholder
Micro-Diesitonal
30edo
Tier: B
placeholder
31edo
Tier: S+
placeholder
32edo
Tier: C
placeholder
33edo
Tier: B
placeholder
34edo
Tier: S+
placeholder
35edo
Tier: B-
placeholder
36edo
Tier: A
placeholder
37edo
Tier: A
placeholder
38edo
Tier: D
placeholder
39edo
Tier: C
placeholder
Micro-Diesitonal EDO Recap
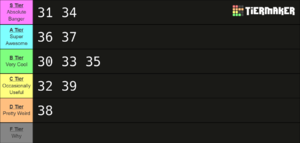
placeholder
Commatonal
40edo
Tier: B
placeholder
41edo
Tier: S+
placeholder
42edo
Tier: D
placeholder
43edo
Tier: A-
placeholder
44edo
Tier: C
placeholder
45edo
Tier: C
placeholder
46edo
Tier: A
placeholder
47edo
Tier: D
placeholder
48edo
Tier: B
placeholder
49edo
Tier: D
placeholder
50edo
Tier: S
placeholder
Commatonal EDO Recap

placeholder